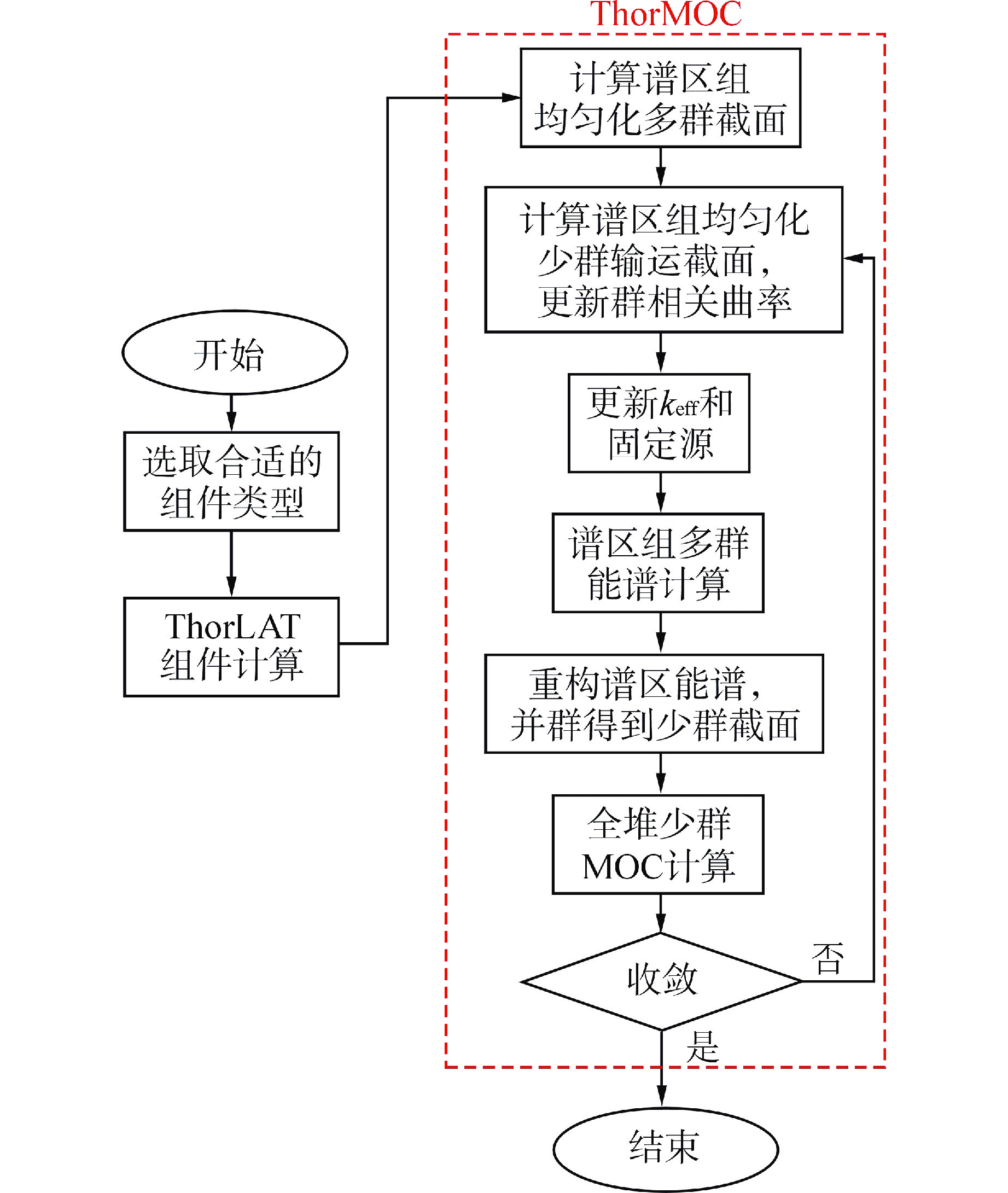
Generation of the Few-Group Cross Sections for Molten Salt Reactors Based on Non-Uniform Spectra Modification Method
-
摘要: 针对熔盐堆高泄漏及强异质性特点,基于特征线方法(MOC)的全堆输运计算适用于熔盐堆临界计算。为权衡计算效率及精度,提出非均匀谱修正(nSM)方法为MOC全堆计算提供少群截面。该方法是一种嵌入式泄漏修正方法,即利用少群MOC全堆计算反馈的泄漏参数进行多群能谱计算,然后在线更新全堆计算的少群截面。针对熔盐实验堆(MSRE)二维全堆基准题,与蒙卡程序OpenMC连续能量计算结果对比,非均匀谱修正方法计算的keff偏差小于0.25%,全堆最大裂变率偏差为2.6%,位于相对裂变率仅0.04的堆容器节块,其计算结果明显优于使用组件计算能谱并群截面方案结果。计算分析表明,引入近似的非均匀谱修正方法具有较好精度,且能显著提高计算效率,是一种能为熔盐堆MOC全堆计算提供少群截面的可行方法。
-
关键词:
- 非均匀谱修正 /
- 熔盐堆 /
- 特征线方法(MOC) /
- 全堆输运计算 /
- 少群截面加工
Abstract: In view of the high leakage and strong heterogeneity of molten salt reactors, the whole-core transport calculation based on the method of characteristic (MOC) is suitable for the critical calculation of molten salt reactors. To balance computational efficiency and accuracy, the non-uniform spectra modification (nSM) method is proposed to generate the few-group cross sections for MOC whole-core calculations. This method is an embedded leakage modification method, which utilizes the leakage parameters obtained by the few-group MOC whole-core calculation for multi-group spectrum calculations, thereby online updating the few-group cross sections of the whole-core calculation. Compared with results from the continuous energy Monto Carlo code OpenMC for the MSRE two-dimensional whole-core benchmark problems, the keff errors calculated by nSM method are less than 0.25% and the maximum error of 2.6% in fission rate distributions occurs at the core can node with a relative fission rate of only 0.04, which are obviously better than those using the cross sections collapsed by the spectra calculated by assembly calculations. The results show that the approximate nSM method still has good accuracy, and could significantly improve the calculation efficiency. Therefore, nSM method could be a feasible method that provides few-group cross sections for the MOC whole-core calculation of molten salt reactors. -
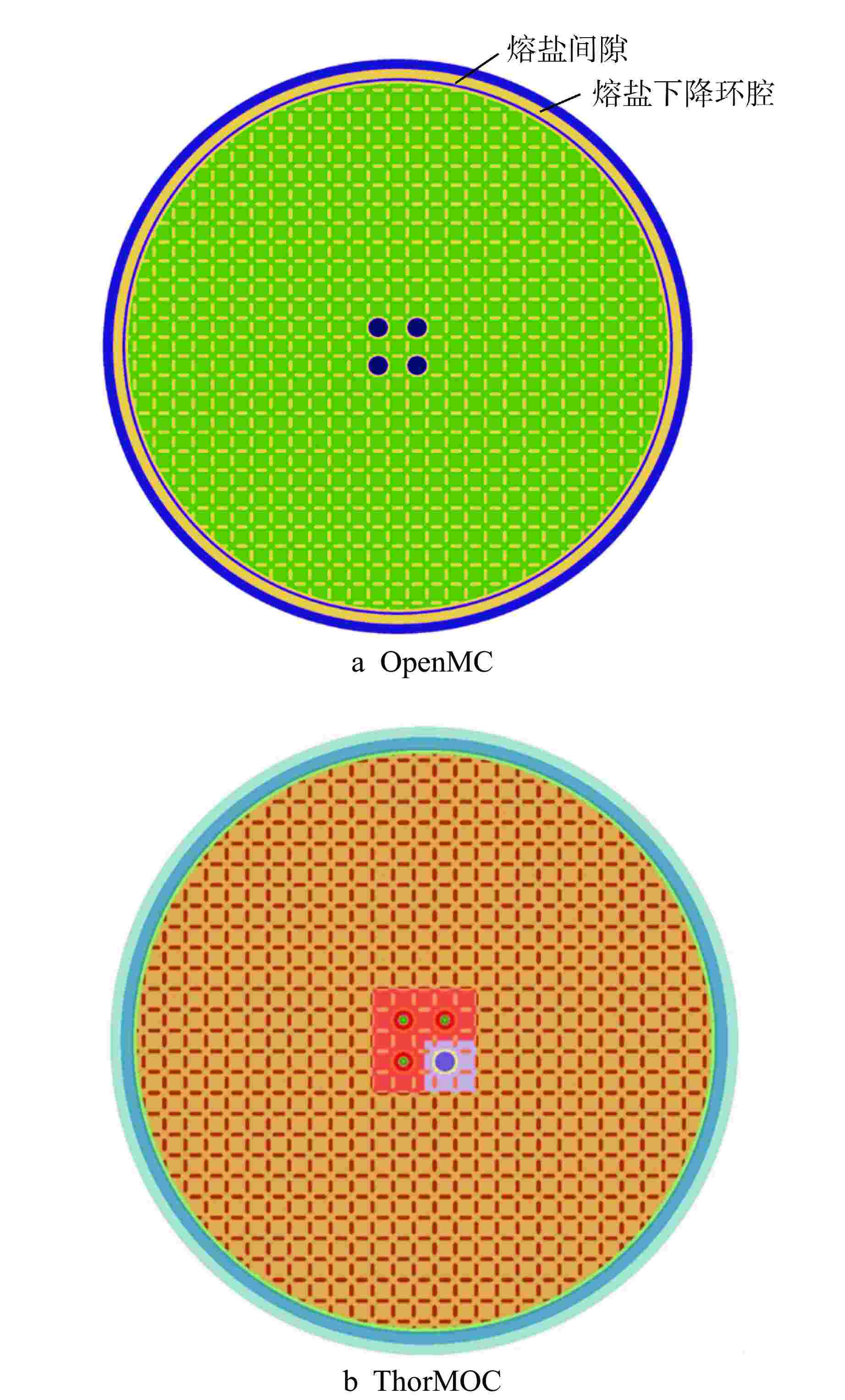
表 1 MSRE二维模型几何尺寸
Table 1. Geometric Parameters for 2D MSRE
参数 数值 燃料组件边长/cm 5.08339 熔盐通道宽度/cm 1.01770 熔盐通道长度/cm 3.05309 控制棒通道半径(材料)/cm 0.2(INOR-8)/1.003(He)/
1.397(Gd2O3-Al2O3)/
2.3476(He)/2.5(INOR-8)堆芯石墨构件半径/cm 70.28500 内容器内外半径/cm 71.09700/71.73700 外容器内外半径/cm 74.29900/76.86200 表 2 各材料的核素原子密度
Table 2. Atomic Densities of Materials
材料 核素 原子密度/1024cm−1 核素 原子密度/1024cm−1 核素 原子密度/1024cm−1 燃料 235U 8.42392×10−5 238U 1.80937×10−4 234U 8.40645×10−7 236U 3.57205×10−7 6Li 1.09381×10−6 7Li 2.18754×10−2 9Be 9.86950×10−3 19F 4.95057×10−2 90Zr 8.77846×10−4 91Zr 1.91432×10−4 92Zr 2.92607×10−4 94Zr 3.44306×10−4 石墨① 12C 9.32817×10−2 INOR-8② 58Ni 4.14052×10−2 60Ni 1.59493×10−2 61Ni 6.93301×10−4 62Ni 2.21057×10−3 64Ni 5.62963×10−4 100Mo 9.06329×10−4 92Mo 1.36255×10−3 94Mo 8.54518×10−4 96Mo 1.55082×10−3 97Mo 8.91259×10−4 98Mo 2.25949×10−3 54Fe 2.74731×10−4 56Fe 4.31268×10−3 57Fe 9.95987×10−5 58Fe 1.32548×10−5 50Cr 3.07082×10−4 52Cr 5.92181×10−3 53Cr 6.71480×10−4 54Cr 1.67145×10−4 12C 2.62315×10−4 46Ti 2.26203×10−5 47Ti 2.03994×10−5 48Ti 2.02129×10−4 49Ti 1.48334×10−5 50Ti 1.42028×10−5 27Al 4.86420×10−4 32S 3.11217×10−5 33S 2.45166×10−7 34S 1.37399×10−6 36S 4.77431×10−9 55Mn 9.55575×10−4 28Si 1.72394×10−3 29Si 8.75367×10−5 30Si 5.77059×10−5 63Cu 1.99944×10−4 65Cu 8.92016×10−5 10B 1.92371×10−5 11B 3.89319×10−5 182W 3.78364×10−5 183W 2.04316×10−5 184W 4.37474×10−5 186W 4.05919×10−5 31P 2.54232×10−5 59Co 1.78159×10−4 Gd2O3-Al2O3 152Gd 3.48303×10−5 154Gd 3.79650×10−4 155Gd 2.57744×10−3 156Gd 3.56488×10−3 157Gd 2.72548×10−3 158Gd 4.32594×10−3 160Gd 3.80696×10−3 27Al 7.45896×10−3 16O 3.72236×10−2 17O 1.41414×10−5 注:①所有计算都忽略石墨晶格对热中子散射影响;②INOR-8中95Mo的共振自屏对反应性有明显影响,但Draglib多群库中没有其共振积分表,按反应性等效以10B进行替换 表 3 组件计算的keff对比
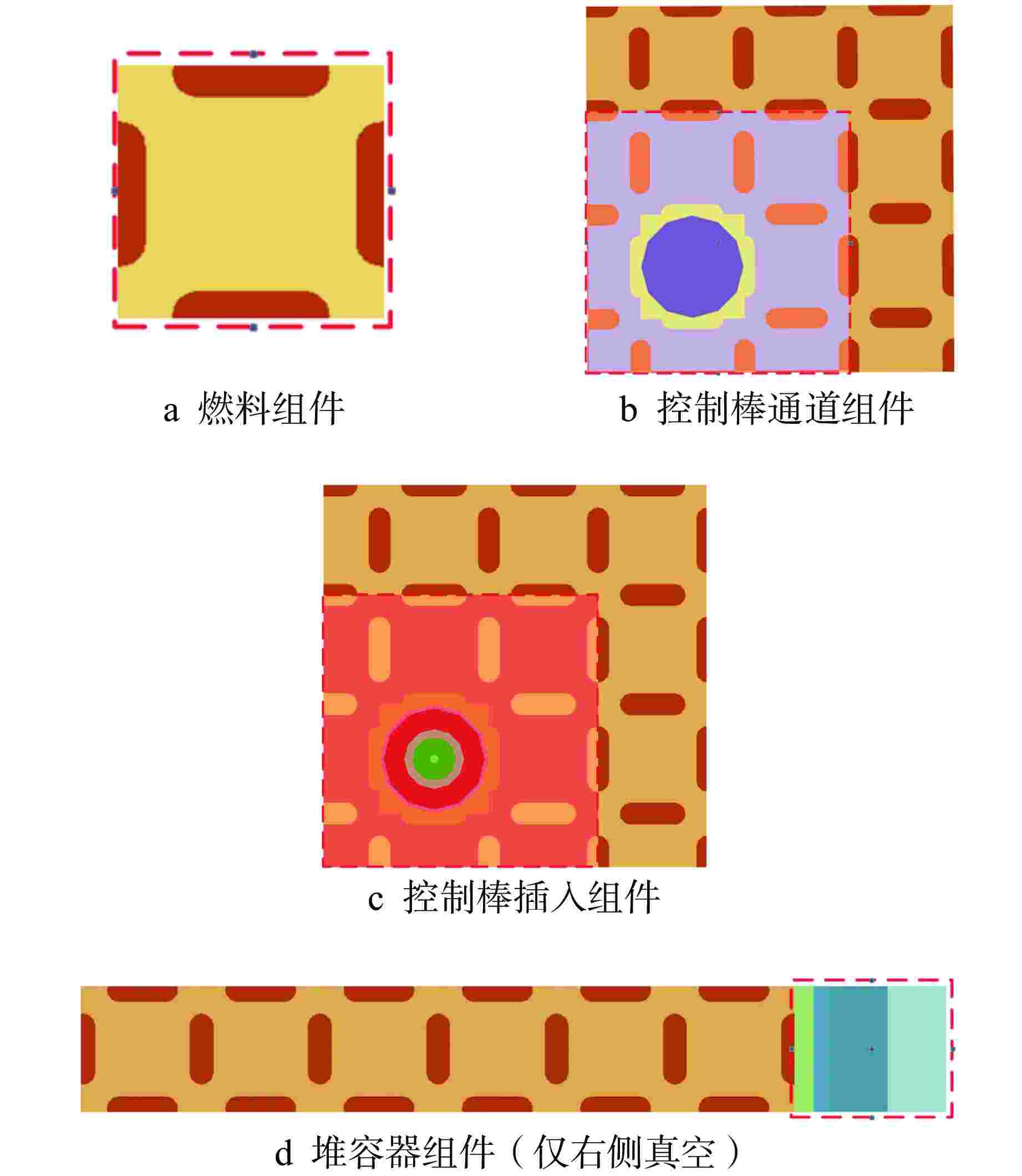
Table 3. keff Comparison for Assembly Calculations
组件类型 OpenMC ThorLAT 偏差/pcm 燃料组件 1.63030±0.00026 1.62990 −25 控制棒通道组件 1.34848±0.00044 1.35013 122 控制棒插入组件 0.70621±0.00035 0.70630 13 堆容器组件 0.93429±0.00029 0.93505 81 1pcm=10−5 表 4 keff及计算时间对比
Table 4. Comparison of keff and Computation Time
控制棒未插入 控制棒插入 keff 偏差/pcm 时间/s keff 偏差/pcm 时间/s OpenMC 1.27507±0.00004 35655 1.03412±0.00004 29640 ThorMOC-11g 1.28232 569 23 1.04755 1299 24 ThorMOC-nSM 1.27688 142 35 1.03518 103 38 ThorMOC-361g 1.27570 49 520 1.03464 50 501 表 5 控制棒插入算例的计算性能分析
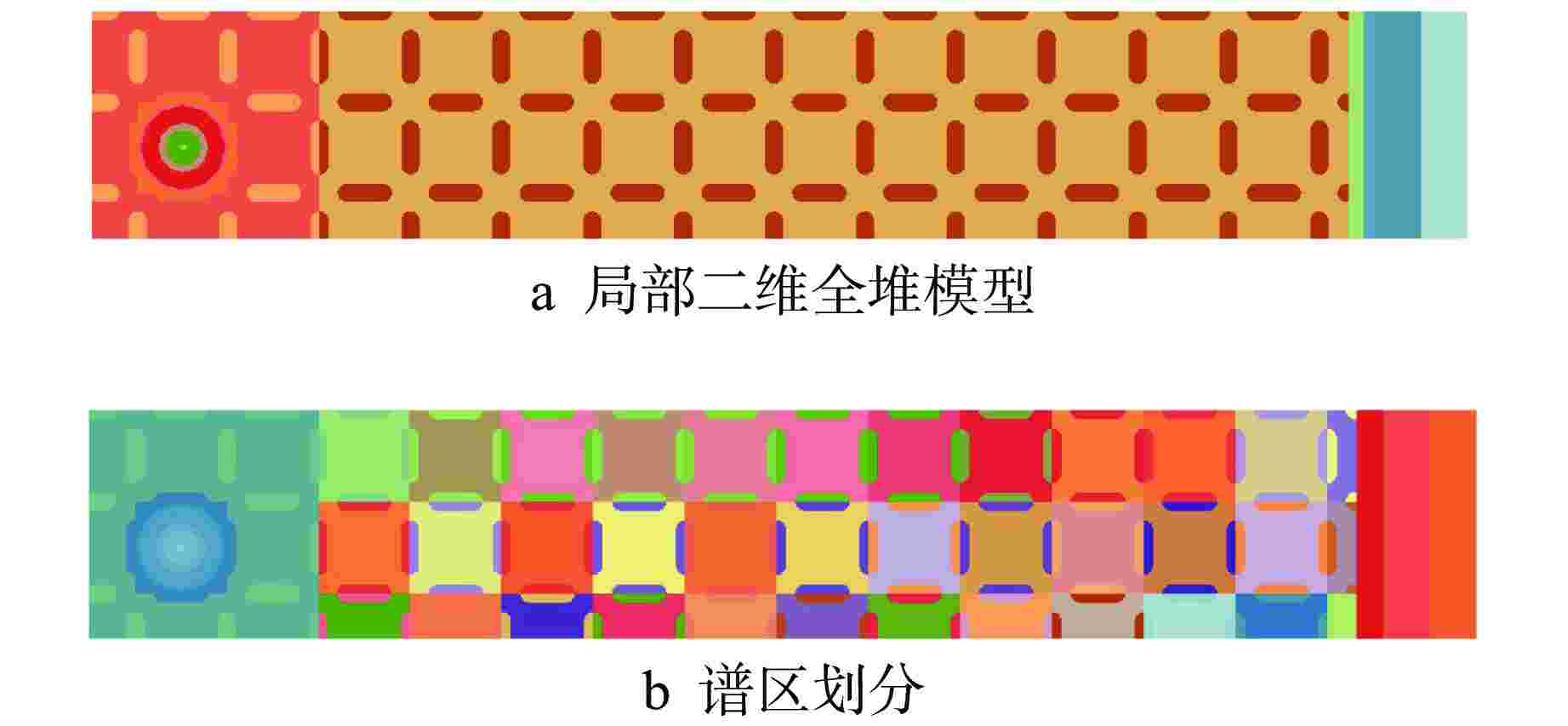
Table 5. Computational Performance Analysis for the Case with Control Rod Inserted
参数 ThorMOC-11g ThorMOC-nSM ThorMOC-361g 特征线生成时间/s 16 16 16 MOC求解时间/s 8 20 485 多群能谱计算时间/s 0 2 0 总外迭代数(曲率及
截面更新次数)26(0) 68(7) 44(0) 显存+内存/GB 0.9+1.1 0.9+1.1 8.3+9.1 表 6 MSRE二维全堆模型的keff及计算时间对比
Table 6. Comparison of keff and Computation Time for MSRE 2D Models
控制棒未插入 控制棒插入 keff 偏差 / pcm 时间/s keff 偏差/pcm 时间/s OpenMC 1.12868±0.00003 64065 1.04374±0.00003 62771 ThorMOC-11g 1.14172 1155 1170 1.05843 834 1179 ThorMOC-nSM 1.13144 245 1434 1.04575 194 1430 ThorMOC-361g 1.13094 200 3448* 1.04599 216 3456* *仅该算例采用二维求解器,计算时间将明显少于三维求解器 表 7 MSRE 二维全堆模型的裂变率分布对比
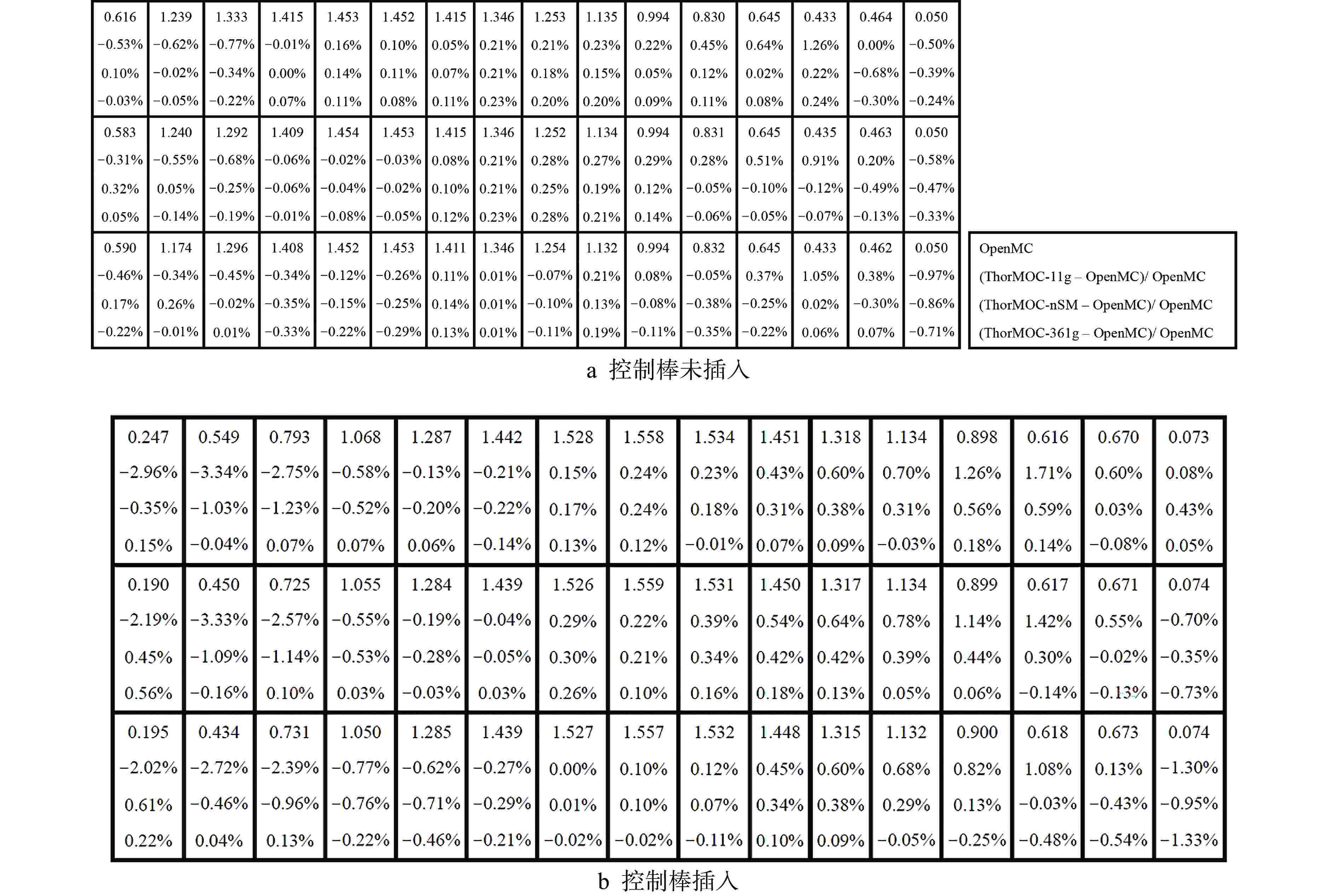
Table 7. Results of Fission Rate Distributions for MSRE 2D Models
控制棒未插入 控制棒插入 MAX(对应相对裂变率) AVG RMS MAX(对应相对裂变率) AVG RMS ThorMOC-11g 2.6%(0.03) 0.4% 0.7% 3.2%(0.04) 0.6% 0.9% ThorMOC-nSM 2.4%(0.40) 0.5% 0.7% 2.6%(0.04) 0.4% 0.6% ThorMOC-361g 1.0%(0.48) 0.3% 0.4% 1.9%(0.12) 0.3% 0.4% MAX—最大绝对值偏差;AVG—平均绝对值偏差;RMS—均方根偏差 -
[1] FRATONI M, SHEN D, ILAS G, et al. Molten salt reactor experiment benchmark evaluation:DOE-UCB-8542[R]. Berkeley: University of California, Berkeley, 2020. [2] 蔡翔舟,戴志敏,徐洪杰. 钍基熔盐堆核能系统[J]. 物理,2016, 45(9): 578-590. doi: 10.7693/wl20160904 [3] 于世和,刘亚芬,杨璞,等. 熔盐实验堆堆芯结构变化对反应性的影响分析[J]. 核技术,2019, 42(2): 020603. doi: 10.11889/j.0253-3219.2019.hjs.42.020603 [4] 戴明,张奥,程懋松. ESSM和Tone方法在熔盐堆共振计算中的适用性分析[J]. 核技术,2022, 45(9): 090605. [5] 戴明,朱贵凤,戴叶,等. 超级均匀化方法用于球床氟盐冷却高温堆扩散计算[J]. 核技术,2017, 40(9): 090604. [6] 戴明,朱贵凤,戴叶,等. 基于CITATION-ORIGEN2球床堆平衡态计算程序的实现[J]. 原子能科学技术,2017, 51(1): 113-119. doi: 10.7538/yzk.2017.51.01.0113 [7] MPHAHLELE R, OUGOUAG A M, IVANOV K N, et al. Spectral zone selection methodology for pebble bed reactors[J]. Annals of Nuclear Energy, 2011, 38(1): 80-87. doi: 10.1016/j.anucene.2010.08.014 [8] RÜTTEN H J, HAAS K A, BROCKMANN H, et al. V. S. O. P. (99/05) computer code system for reactor physics and fuel cycle simulation:Jül-4189[R]. Jülich: Forschungszentrum Jülich GmbH, 2005. [9] HUDSON N H, OUGOUAG A M, RAHNEMA F, et al. A pebble bed reactor cross section methodology[J]. Annals of Nuclear Energy, 2009, 36(8): 1138-1150. doi: 10.1016/j.anucene.2009.04.013 [10] MASSIMO L. Physics of high-temperature reactors[M]. Oxford: Pergamon Press, 1976:208-210. [11] SHE D, LIU Z H, GUO J, et al. Leakage correction in group-constant generation for pebble-bed HTGRs[J]. Progress in Nuclear Energy, 2018, 105: 76-82. doi: 10.1016/j.pnucene.2017.12.015 [12] 戴明. 球床氟盐冷却高温堆堆芯燃料管理研究[D]. 上海: 中国科学院研究生院(上海应用物理研究所),2017: 37-42. [13] DAI M, CHENG M S. Application of material-mesh algebraic collapsing acceleration technique in method of characteristics-based neutron transport code[J]. Nuclear Science and Techniques, 2021, 32(8): 87. doi: 10.1007/s41365-021-00923-w [14] ZHANG A, DAI M, CHENG M S, et al. Development of a GPU-based three-dimensional neutron transport code[J]. Annals of Nuclear Energy, 2022, 174: 109156. doi: 10.1016/j.anucene.2022.109156 [15] DAI M, ZHANG A, CHENG M S. Improvement of the 3D MOC/DD neutron transport method with thin axial meshes[J]. Annals of Nuclear Energy, 2023, 185: 109731. doi: 10.1016/j.anucene.2023.109731 [16] ROMANO P K, HORELIK N E, HERMAN B R, et al. OpenMC: a state-of-the-art Monte Carlo code for research and development[J]. Annals of Nuclear Energy, 2015, 82: 90-97. doi: 10.1016/j.anucene.2014.07.048 -





 下载:
下载: