Implementation and Optimization of Function Expansion Tallies Based on Track Length Estimation Method in RMC
-
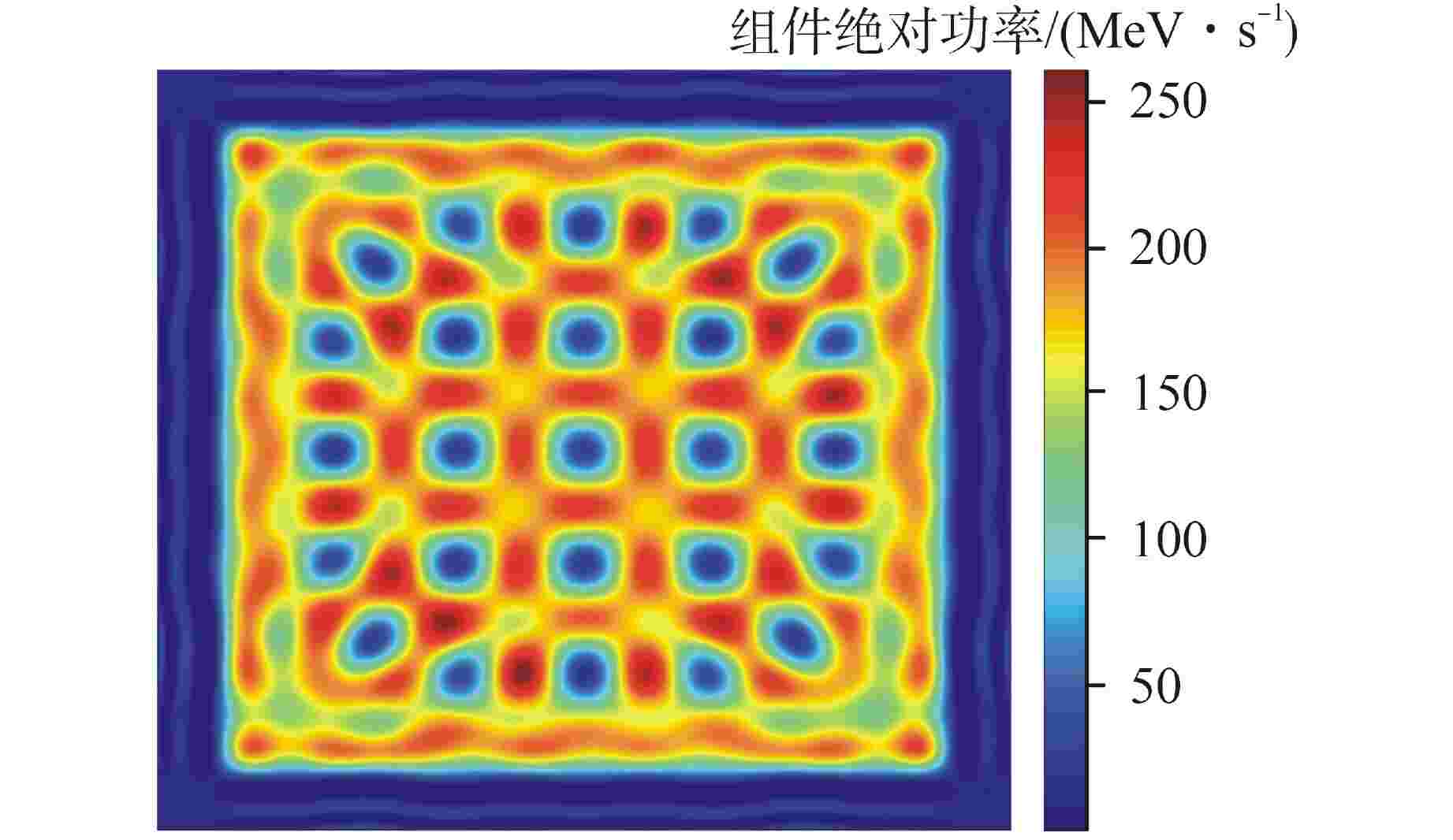
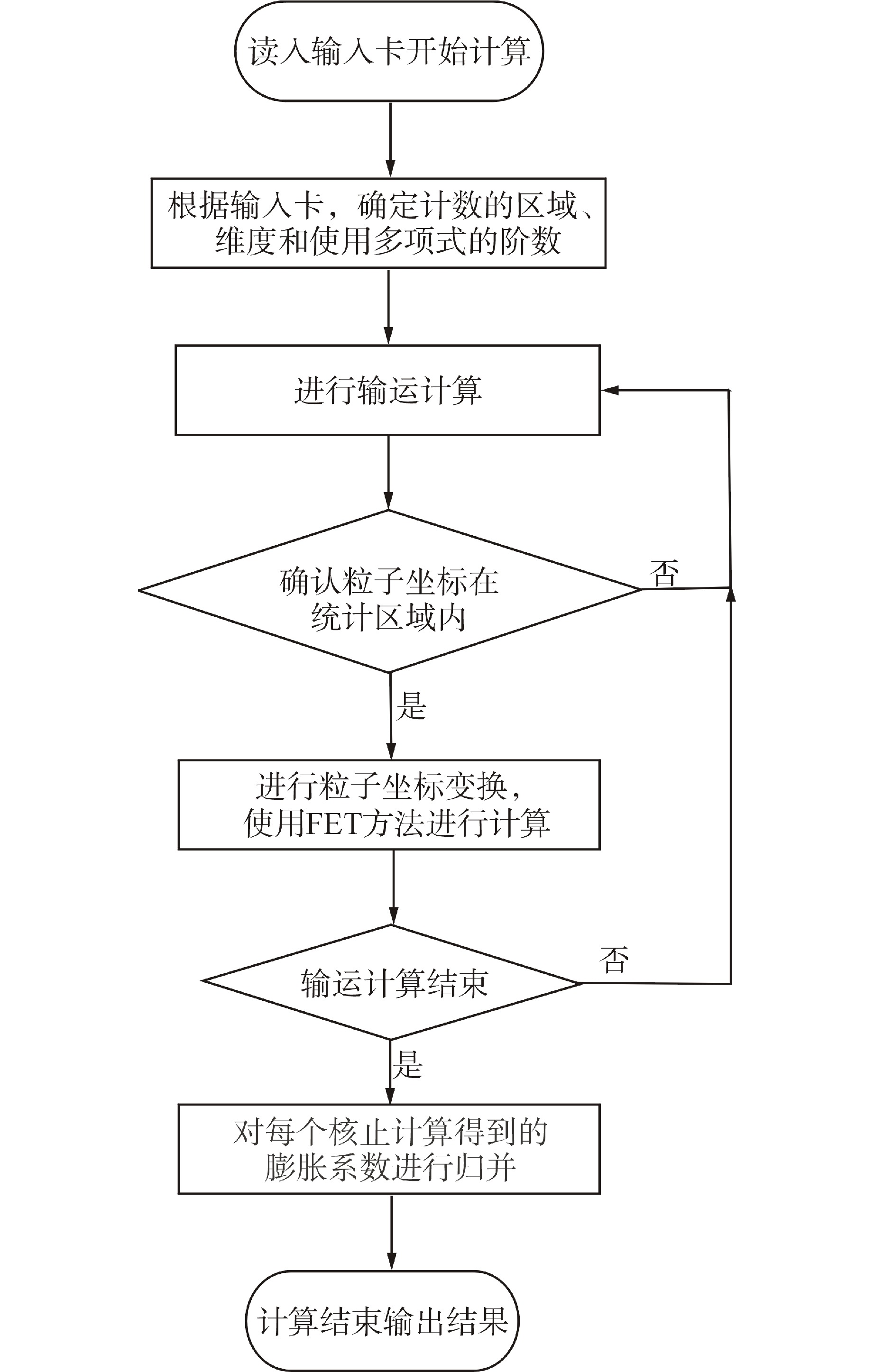
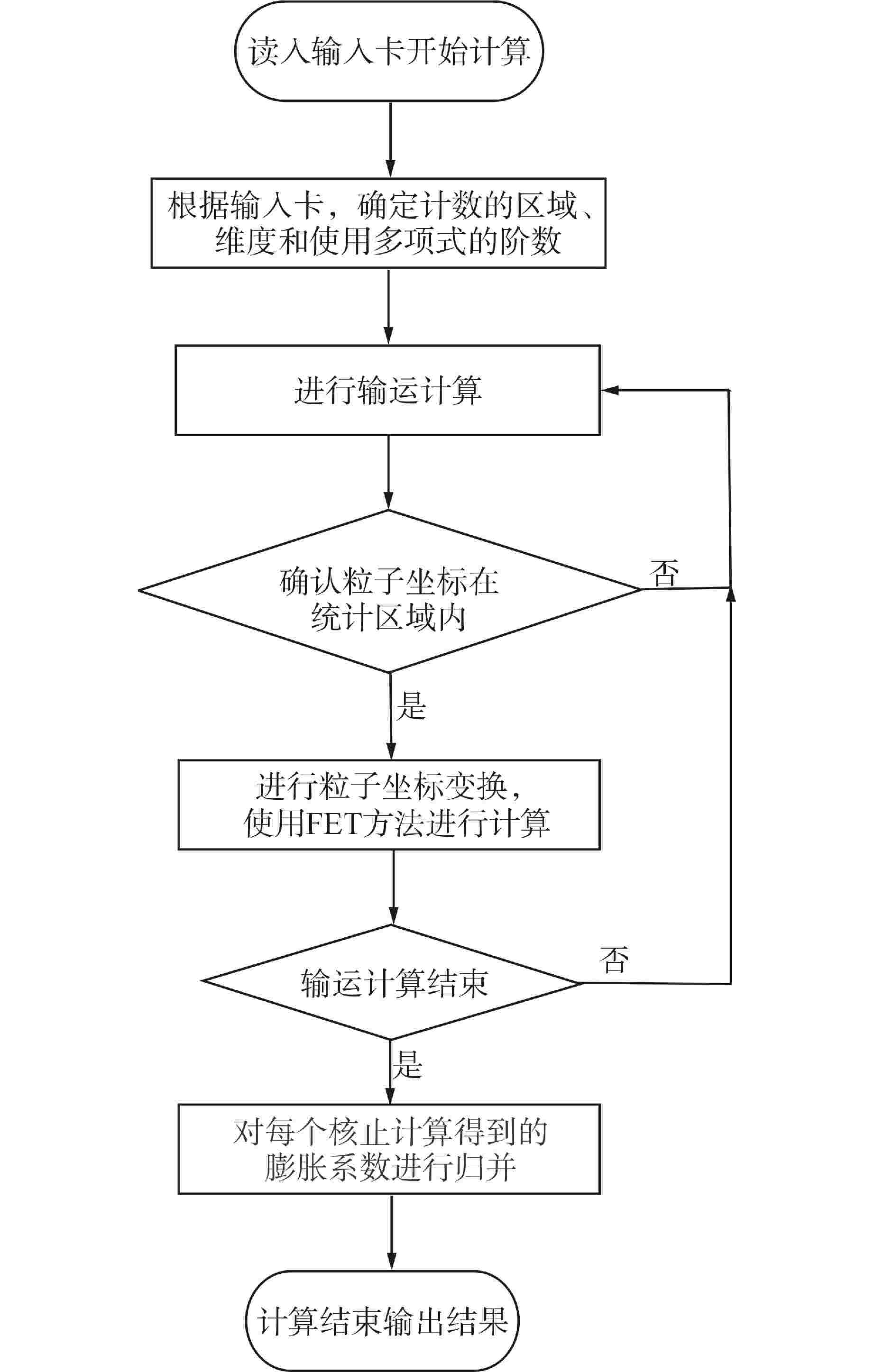
摘要: 传统的蒙特卡罗模拟通常采用分箱计数的方式来进行相关参数统计,粗糙的计数箱划分难以精确地描述一些参数在整个空间中的分布,而细致的计数箱划分则需很大的样本数才能得到满足要求的统计精度,将花费大量的时间。函数展开计数方法(FET方法)可以得到参数在求解空间中的连续分布,并能解决计算效率和精度无法兼得的问题。在蒙特卡罗程序RMC中创新地实现了基于径迹长度估计的FET方法,结合勒让德多项式和泽尼克多项式计算参数在三维组件中的连续分布,同时对比了FET方法与网格计数法的计算耗时。研究结果表明,FET方法的计算结果与网格计数法符合很好,并且计算时间相比网格计数法有所降低,内存占用大大降低。本研究开发的FET方法可用于蒙特卡罗程序的计数研究。
-
关键词:
- RMC /
- 函数展开计数方法(FET方法) /
- 径迹长度估计 /
- 三维组件空间函数展开
Abstract: Traditional Monte Carlo simulations usually use bin-counting to statistically analyze relevant parameters. Rough bin division is difficult to accurately describe the distribution of some parameters in the whole space, while detailed bin division requires a large number of samples to meet the required statistical accuracy, which will take a lot of time. The functional expansion tallies method (FET method) can obtain the continuous distribution of parameters in the solution space, and can solve the problem that computational efficiency and accuracy cannot be achieved at the same time. The FET method based on track-length estimation is innovatively implemented in Monte Carlo Code (RMC). In addition, the Legendre polynomials and Zernike polynomials are combined to calculate the continuous distribution of the parameters in the three-dimensional assembly space. At the same time, the simulation time of FET method and meshtally method are compared. The results show that the calculation results of FET method are in good agreement with the meshtally method, and the simulation time of FET method is reduced while the simulation memory is greatly reduced. Therefore, the functional expansion tallies method developed in this study can be used in Monte Carlo code. -
表 1 2种方法的一维计算时间和内存占用对比
Table 1. Simulation Time and Memory Occupation of Two Methods in One-dimensional Problem
方法 计算时间 / min 内存占用 6阶勒让德多项式,FET方法 0.280 O (6) 40 个网格数目,网格计数法 0.272 O (40) 100 个网格数目,网格计数法 0.287 O (100) 1000 个网格数目,网格计数法 0.410 O (1000) O(n)—计算运行内存占用的字节数 表 2 2种方法的二维计算时间和内存占用对比
Table 2. Simulation Time and Memory Occupation of Two Methods in Two-dimensional Problem
方法 计算时间 / min 内存占用 6 阶泽尼克多项式,FET方法 0.575 O (28) 6×6 网格数目,网格计数法 0.309 O (36) 10×100 网格数目,网格计数法 0.612 O (10000) 1000×1000 网格数目,网格计数法 1.641 O (1000000) 表 3 2种方法的三维计算时间及内存占用对比
Table 3. Simulation Time and Memory Occupation of Two Methods in Three-dimensional Problem
方法 计算时间 / min 内存占用 2×25×25 阶勒让德多项式,
FET方法0.367 O (1250) 10×17×17 网格数目,
网格计数法0.260 O (2890) 10×100×100 网格数目,
网格计数法0.445 O (100000) 10×1000×1000 网格数目,
网格计数法内存溢出,无法计算 O (10000000) -
[1] GRIESHEIMER D P, MARTIN W R. Two dimensional functional expansion tallies for Monte Carlo simulations[C]//The Physics of Fuel Cycles and Advanced Nuclear Systems: Global Developments. Chicago: American Nuclear Society, 2004. [2] 潘流俊,沈华韵,衷斌. 泛函展开计数在蒙特卡罗界面流角度谱计算中的应用[J]. 原子能科学技术,2014, 48(S1): 128-130. [3] ROMANO P K, FORGET B. The OpenMC Monte Carlo particle transport code[J]. Annals of Nuclear Energy, 2013, 51: 274-281. doi: 10.1016/j.anucene.2012.06.040 [4] ELLIS M, GASTON D, FORGET B, et al. Preliminary coupling of the Monte Carlo code OpenMC and the multiphysics object-oriented simulation environment for analyzing Doppler feedback in Monte Carlo simulations[J]. Nuclear Science and Engineering, 2017, 185(1): 184-193. doi: 10.13182/NSE16-26 [5] NOVAK A, ROMANO P, WENDT B, et al. Preliminary coupling of OpenMC and Nek5000 within the MOOSE framework[C]//Proceedings of the International Conference on Physics of Reactors (PHYSOR 2018): volume 4. Cancun, Mexico, 2018. [6] LEE H. Development of a new Monte Carlo code for large-scale power reactors analysis[D]. Ulsan: Ulsan National Institute of Science and Technology, 2019. [7] YU J K, LEE H, LEMAIRE M, et al. MCS based neutronics/thermal-hydraulics/fuel-performance coupling with CTF and FRAPCON[J]. Computer Physics Communications, 2019, 238: 1-18. doi: 10.1016/j.cpc.2019.01.001 [8] EBIWONJUMI B, LEE H, ZHANG P, et al. Functional expansion tallies in Monte Carlo high fidelity LWR analysis[C]//Proceedings of the Reactor Physics Asia 2019 (RPHA19) Conference. Osaka, Japan, 2019. [9] WANG K, LI Z G, SHE D, et al. RMC - a Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82: 121-129. doi: 10.1016/j.anucene.2014.08.048 [10] 李泽光. 自主堆用蒙卡程序RMC研发及关键基础算法研究[D]. 北京: 清华大学, 2012.李泽光. 自主堆用蒙卡程序RMC研发及关键基础算法研究[D]. 北京: 清华大学, 2012. [11] AN N, PAN Q Q, GUO X Y, et al. A new functional expansion tallies (FET) method based on cutting track-length estimation in RMC code[J]. Nuclear Engineering and Design, 2022, 391: 111736. doi: 10.1016/j.nucengdes.2022.111736 [12] WANG Z Y, LIU S C, SHE D, et al. Implementation of functional expansion tally method and order selection strategy in Monte Carlo code RMC[J]. Nuclear Engineering and Technology, 2021, 53(2): 430-438. doi: 10.1016/j.net.2020.07.018 -





 下载:
下载: