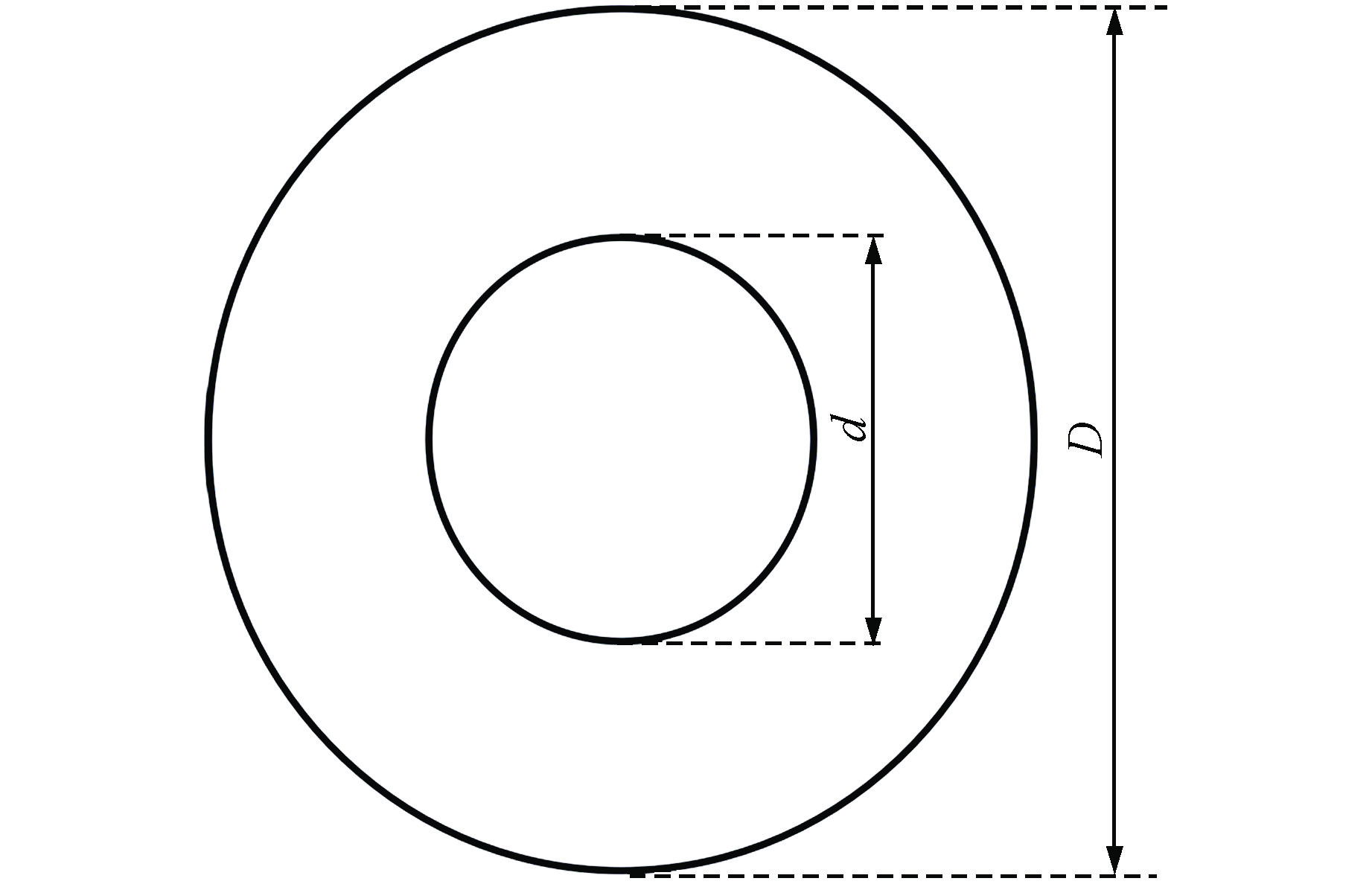
Study on Added Mass and Fluid Damping Characteristics Based on Concentric Cylindrical Structure
-
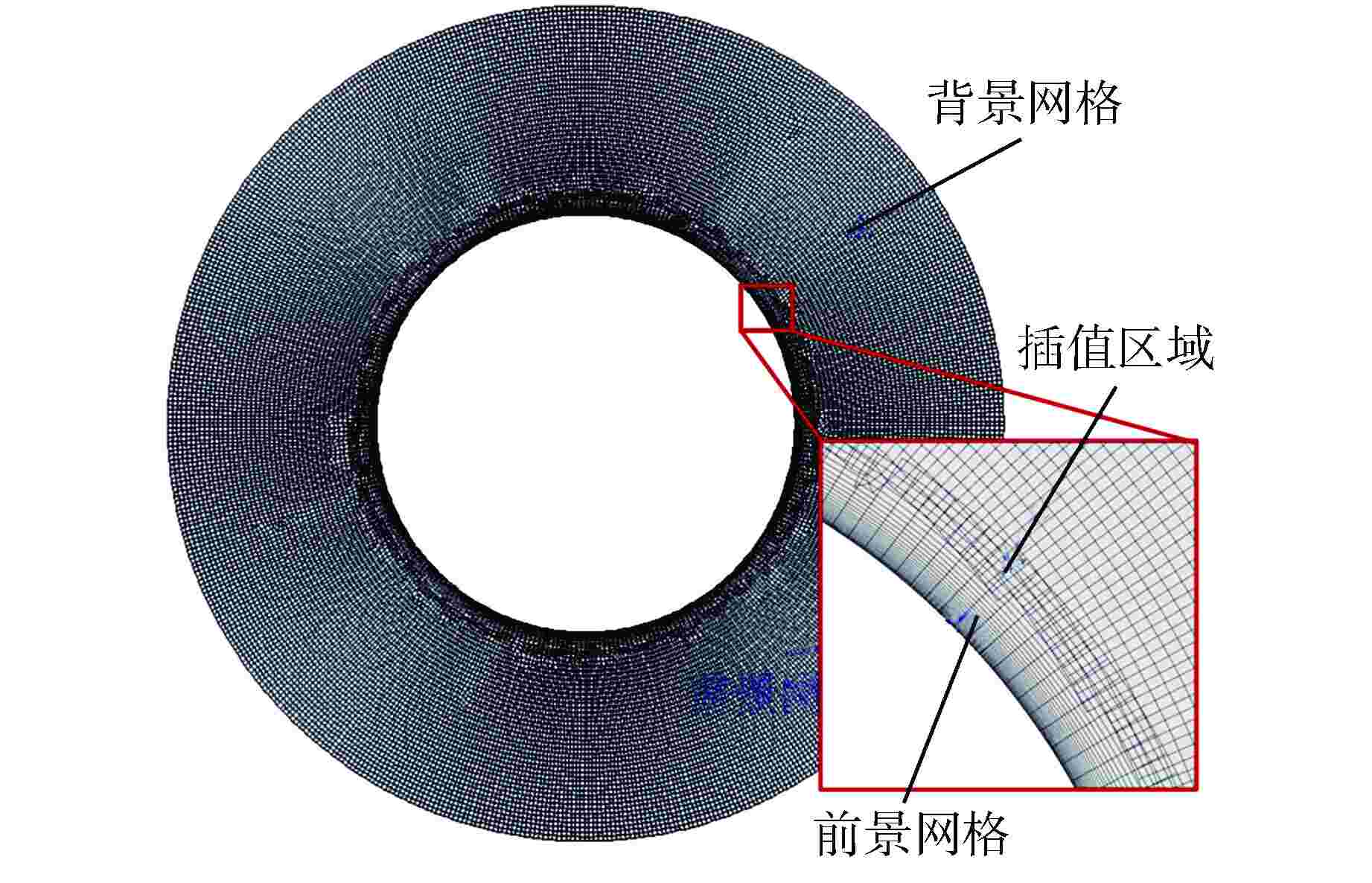
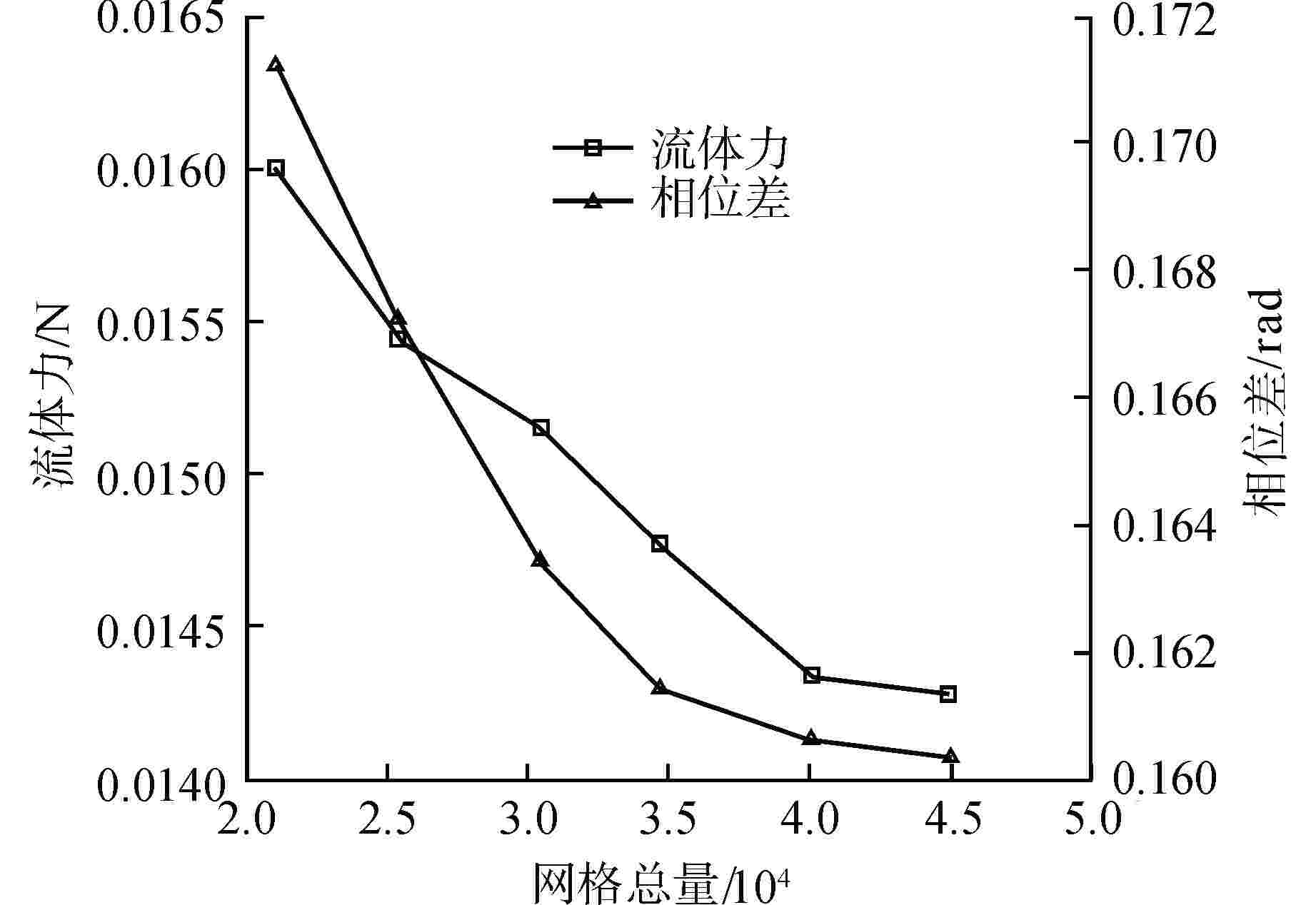
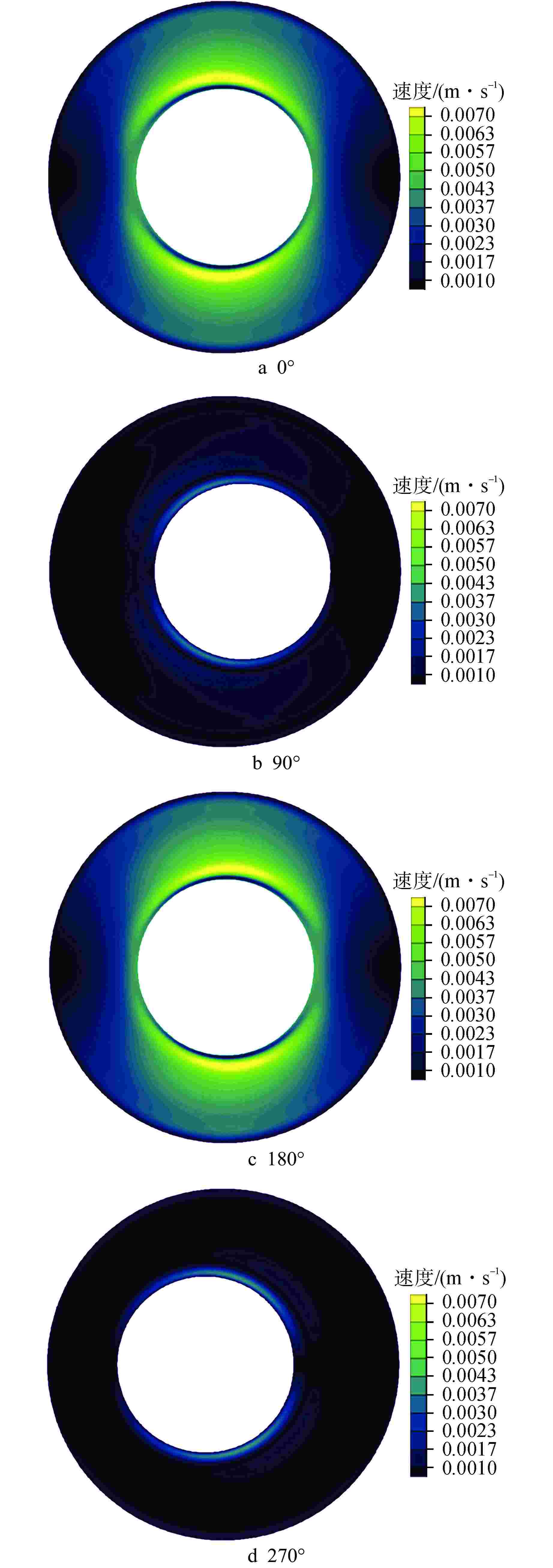
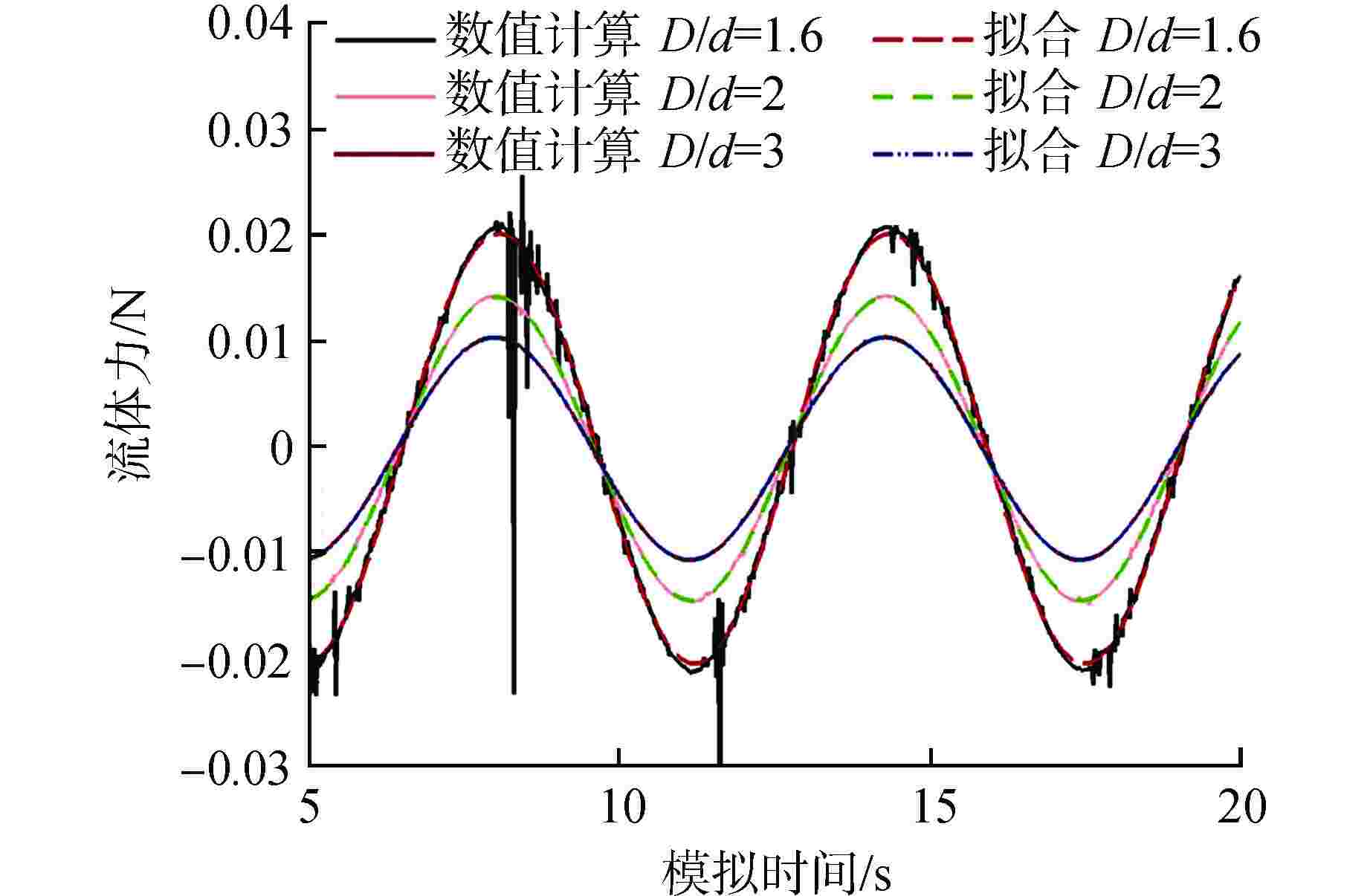
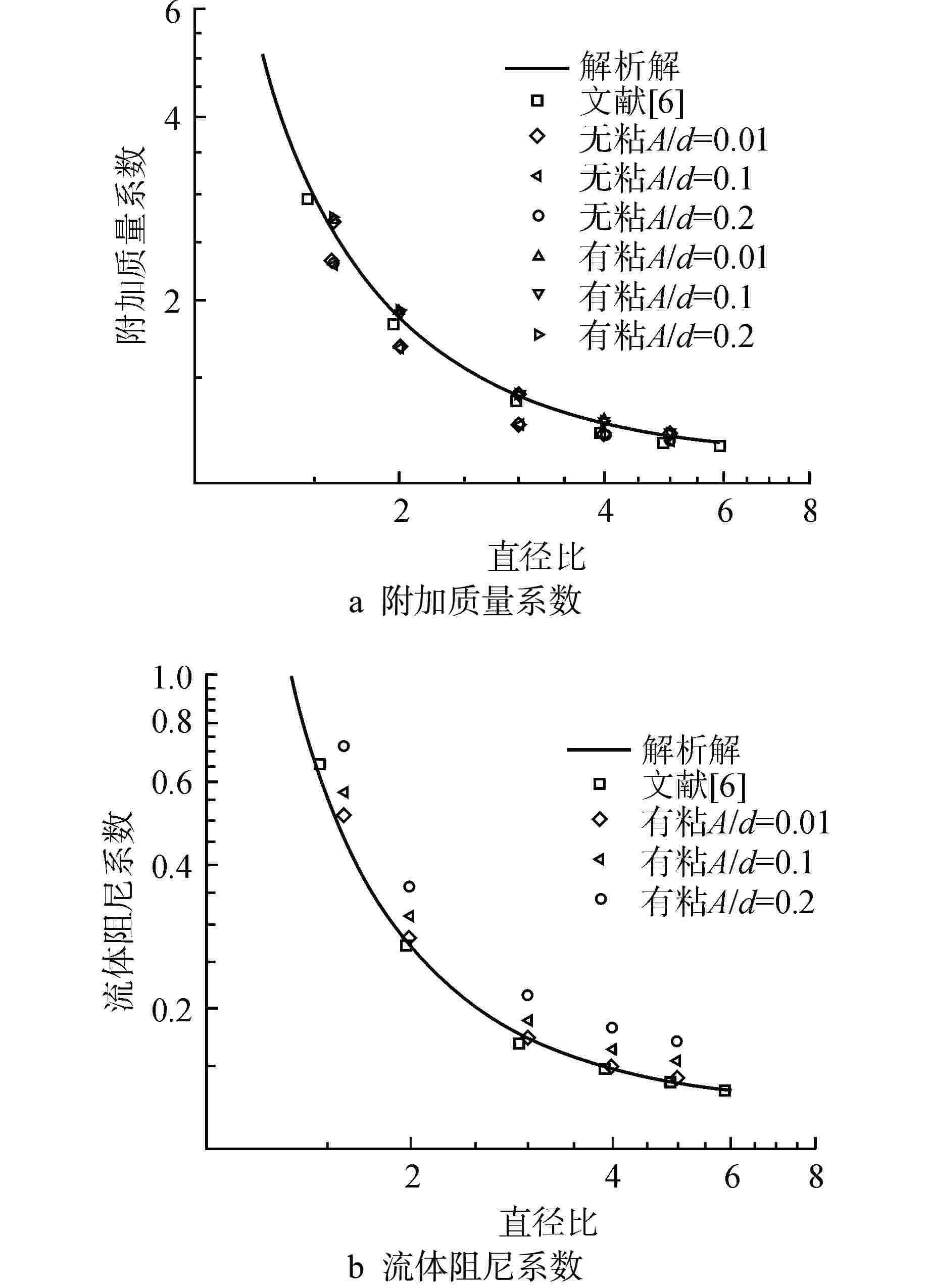
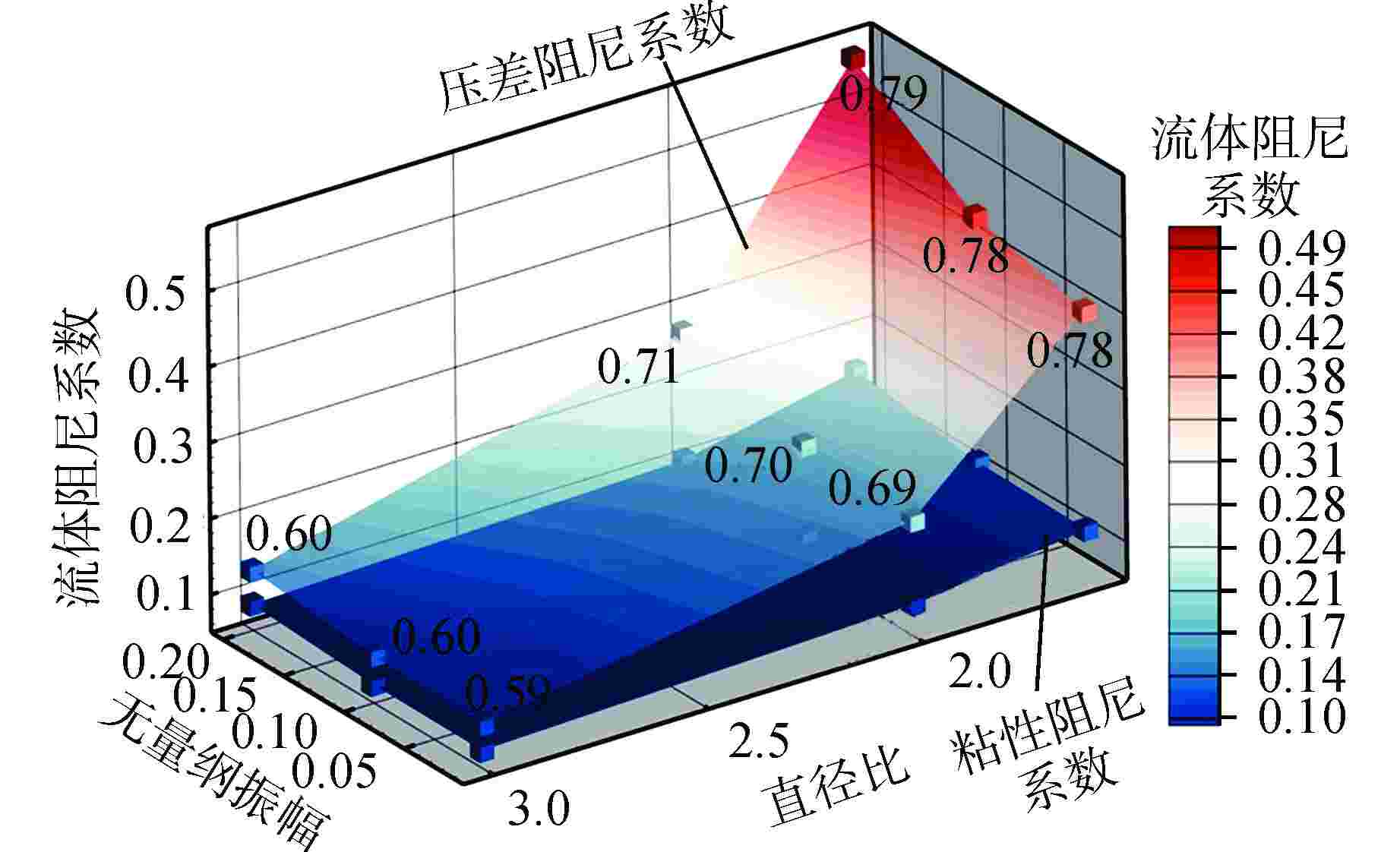
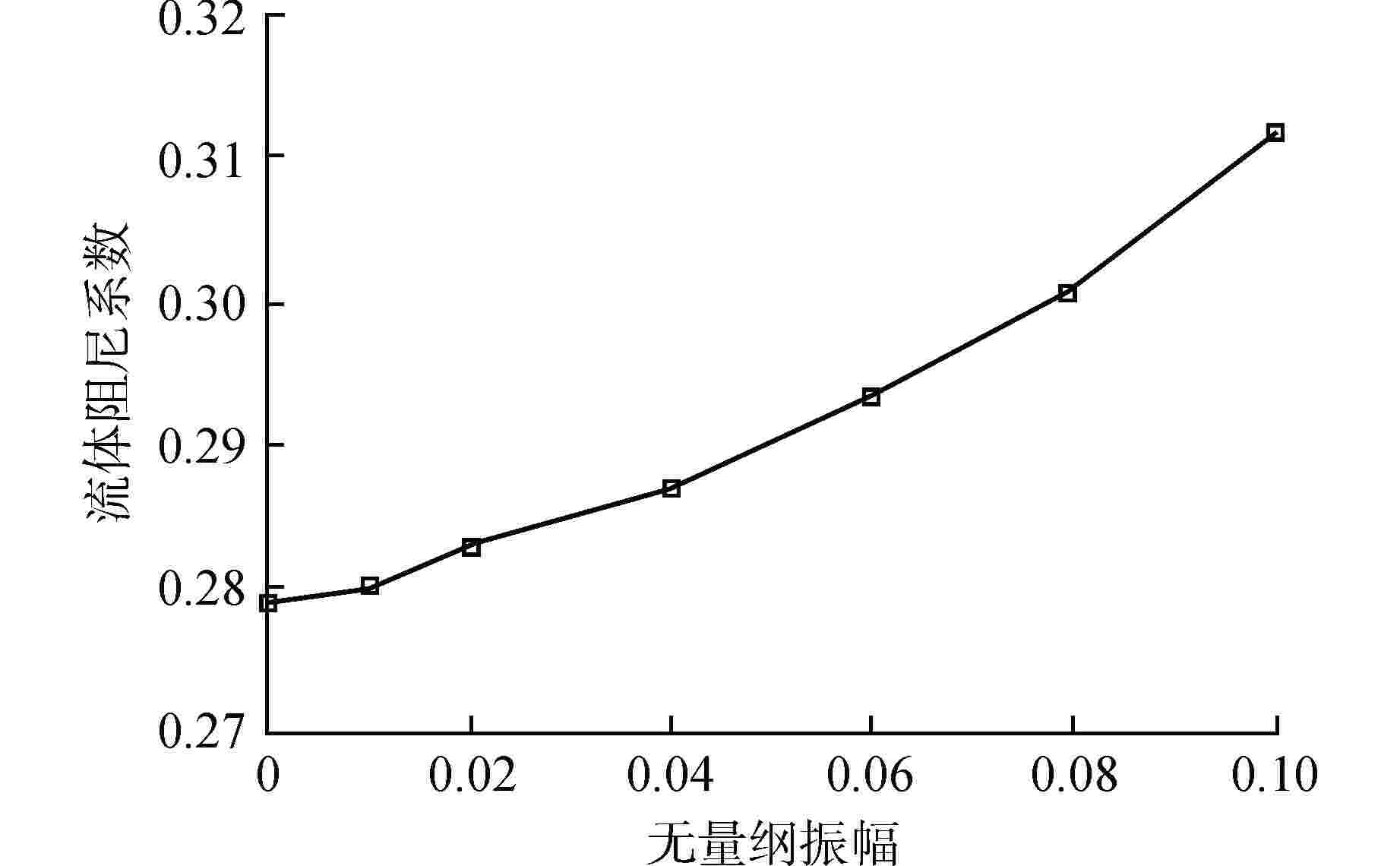
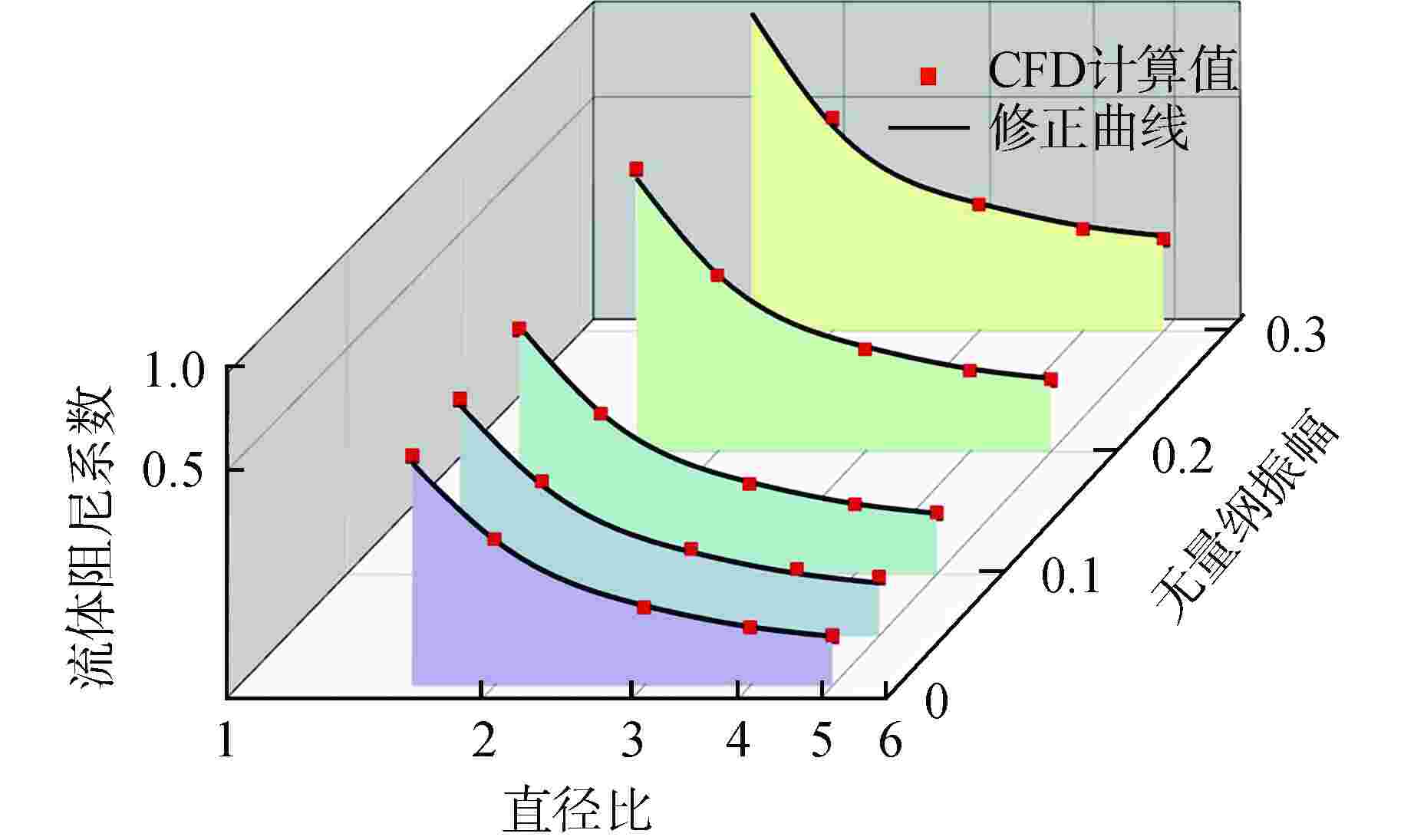
摘要: 为深入探究附加质量与流体阻尼的内在特性，分析粘性与振幅对其的影响，进而为流致振动分析提供指导，本研究以同心结构圆柱为例建立基于计算流体动力学（CFD）的附加质量与流体阻尼预测方法，通过用户自定义函数（UDF）设定内圆运动方程，运用嵌套网格技术完成网格运动，从而实现流场的数值模拟。根据Bearman假设确定函数形状，通过最小二乘法拟合计算所得的流体力曲线，进而得到附加质量与流体阻尼，并对比粘性与无量纲振幅对结果的影响。计算分析结果表明：粘性不仅影响流体阻尼，也影响附加质量；无量纲振幅对附加质量影响甚微，对流体阻尼有明显影响；压差阻尼和粘性阻尼随无量纲振幅的增加而等比例增加，压差阻尼占比随直径比的减小而增加；引入无量纲振幅影响的修正公式解与数值计算结果具有较好的一致性。本文研究对优化现有流致振动分析方法具有重要的指导作用。
-
关键词:
- 用户自定义函数（UDF） /
- 附加质量 /
- 流体阻尼 /
- 无量纲振幅
Abstract: To deeply investigate the intrinsic characteristics of added mass and fluid damping, analyze the impact of viscosity and amplitude on them, and provide guidance for analyzing fluid-induced vibration, this study takes a concentric cylinder as an example to establish a prediction method of added mass and fluid damping based on computational fluid dynamics (CFD). The user-defined function (UDF) is used to set the motion equation of the inner circle, and the overset grid technology is used to complete the grid motion, so as to realize the numerical simulation of the flow field. The shape of the function is determined according to Bearman's hypothesis, and the calculated fluid force curve is fitted by the least square method to obtain the added mass and fluid damping. Finally, the influences of viscosity and dimensionless amplitude on results are compared. The calculation and analysis results show that the viscosity not only affects the fluid damping but also the added mass. The dimensionless amplitude has little effect on the added mass and an obvious effect on the fluid damping. Pressure damping and viscous damping increase in equal proportion with the increase of dimensionless amplitude, and the proportion of pressure damping increases with the decrease of diameter ratio. The solution of the modified formula with dimensionless amplitude effect is in good agreement with the numerical results. The research in this paper has an important guiding role in optimizing the existing analysis methods of flow-induced vibration.-
Key words:
- User-defined function (UDF) /
- Added mass /
- Fluid damping /
- Dimensionless amplitude
-
图 3 流体力振幅与相位差随网格总量变化曲线
Figure 3. Variation Curves of Fluid Force Amplitude and Phase Difference with the Total Mesh Quantity
图 6 附加质量系数与流体阻尼系数随直径比变化图
Figure 6. Variation of Added Mass Coefficient and Fluid Damping Coefficient with Diameter Ratio
图 7 压差/粘性阻尼系数随直径比和无量纲振幅变化的曲面图
图中标记的数值为压差阻尼系数占比
Figure 7. Surface Diagram of Viscosity/Pressure Damping Coefficient with Diameter Ratio and Dimensionless Amplitude
图 8 D/d=2时流体阻尼系数随无量纲振幅变化的曲线
Figure 8. Variation Curve of Fluid Damping Coefficient with Dimensionless Amplitude (D/d=2)
-
[1] CHEN S S, WAMBSGANSS M W, JENDRZEJCZYK J A. Added mass and damping of a vibrating rod in confined viscous fluids[J]. Journal of Applied Mechanics, 1976, 43(2): 325-329. doi: 10.1115/1.3423833 [2] PAULLING J R, PORTER W R. Analysis and measurement of pressure and force on heaving cylinders in a free surface[C]. New York, America: Society of Mechanical EngineersProceedings of the Fourth U. S. National Congress of Applied Mechanics, 1962: 1369-1381. [3] FRITZ R J. The effects of an annular fluid on the vibrations of a long rotor, part 2—test[J]. Journal of Fluids Engineering, 1970, 92(4): 930-937. [4] SINYAVSKII V F, FEDOTOVSKII V S, KUKHTIN A B. Oscillation of a cylinder in a viscous liquid[J]. Soviet Applied Mechanics, 1980, 16(1): 46-50. doi: 10.1007/BF00884613 [5] 林超友,朱军. 潜艇近海底航行附加质量数值计算[J]. 船舶工程,2003, 25(1): 26-29. doi: 10.3969/j.issn.1000-6982.2003.01.007 [6] YANG C I, MORAN T J. Finite-element solution of added mass and damping of oscillation rods in viscous fluids[J]. Journal of Applied Mechanics, 1979, 46(3): 519-523. doi: 10.1115/1.3424599 [7] 李刚,段文洋,郭志彬. 复杂构型潜器附加质量的研究[J]. 哈尔滨工业大学学报,2010, 42(7): 1145-1148. doi: 10.11918/j.issn.0367-6234.2010.07.030 [8] 马烨,单雪雄. 数值计算复杂外形物体附加质量的新方法[J]. 计算机仿真,2007, 24(5): 75-78,113. doi: 10.3969/j.issn.1006-9348.2007.05.022 [9] 约翰 D. 安德森. 计算流体力学基础及其应用[M]. 吴颂平,刘赵淼,译. 北京: 机械工业出版社,2007: 371. [10] 李志旺,严家骏. 一个新的液体状态方程[J]. 工程热物理学报,1990, 11(2): 126-128. [11] 小约翰 D. 安德森. 空气动力学基础[M]. 杨永,宋文萍,张正科,等,译. 第六版. 北京: 航空工业出版社,2020: 1152. -
下载:
计量
- 文章访问数: 65
- HTML全文浏览量: 14
- PDF下载量: 16
- 被引次数: 0
