Acceleration Method and Verification of Theoretical Calculation of Irradiation Supervision for Pressurized Water Reactor
-
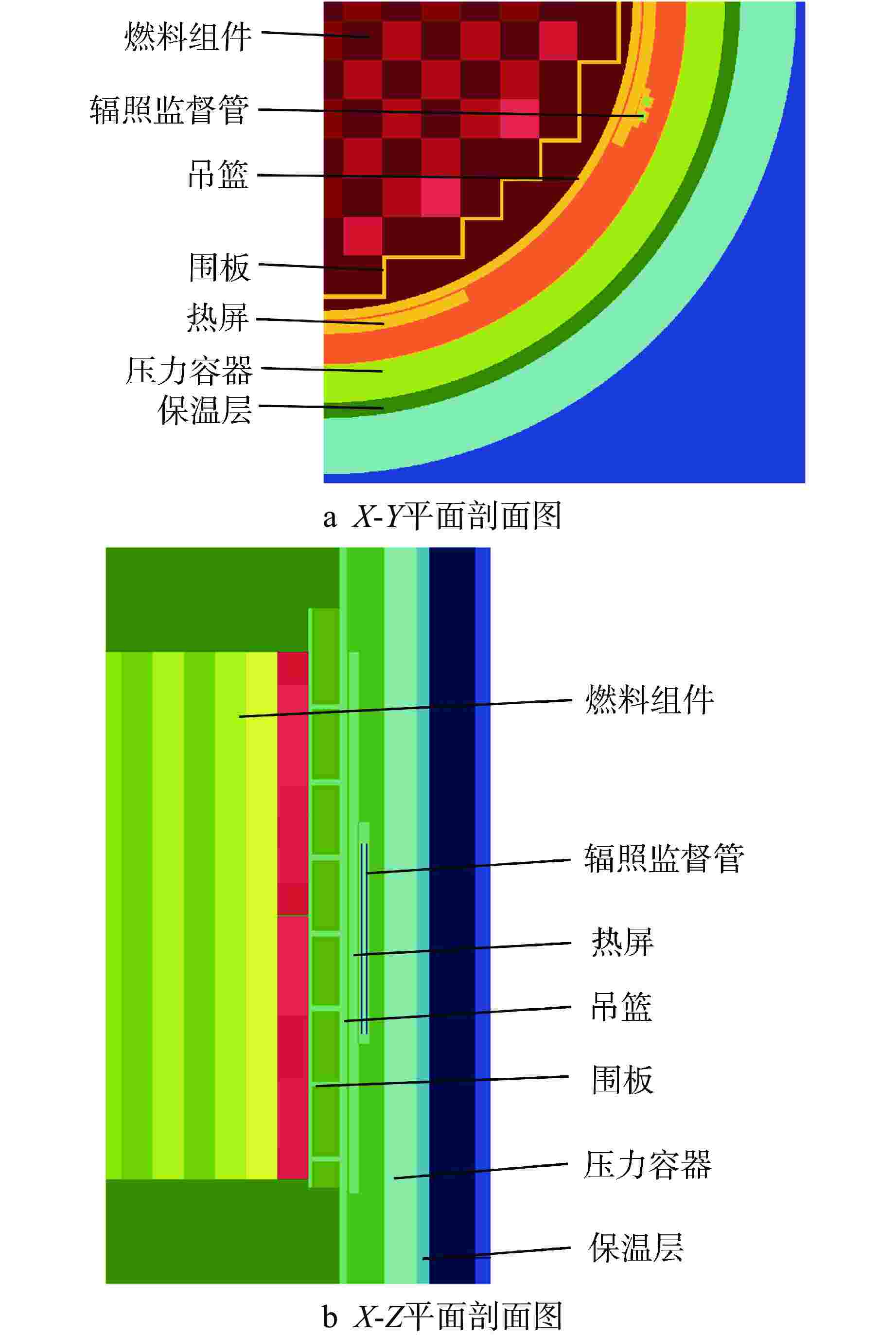
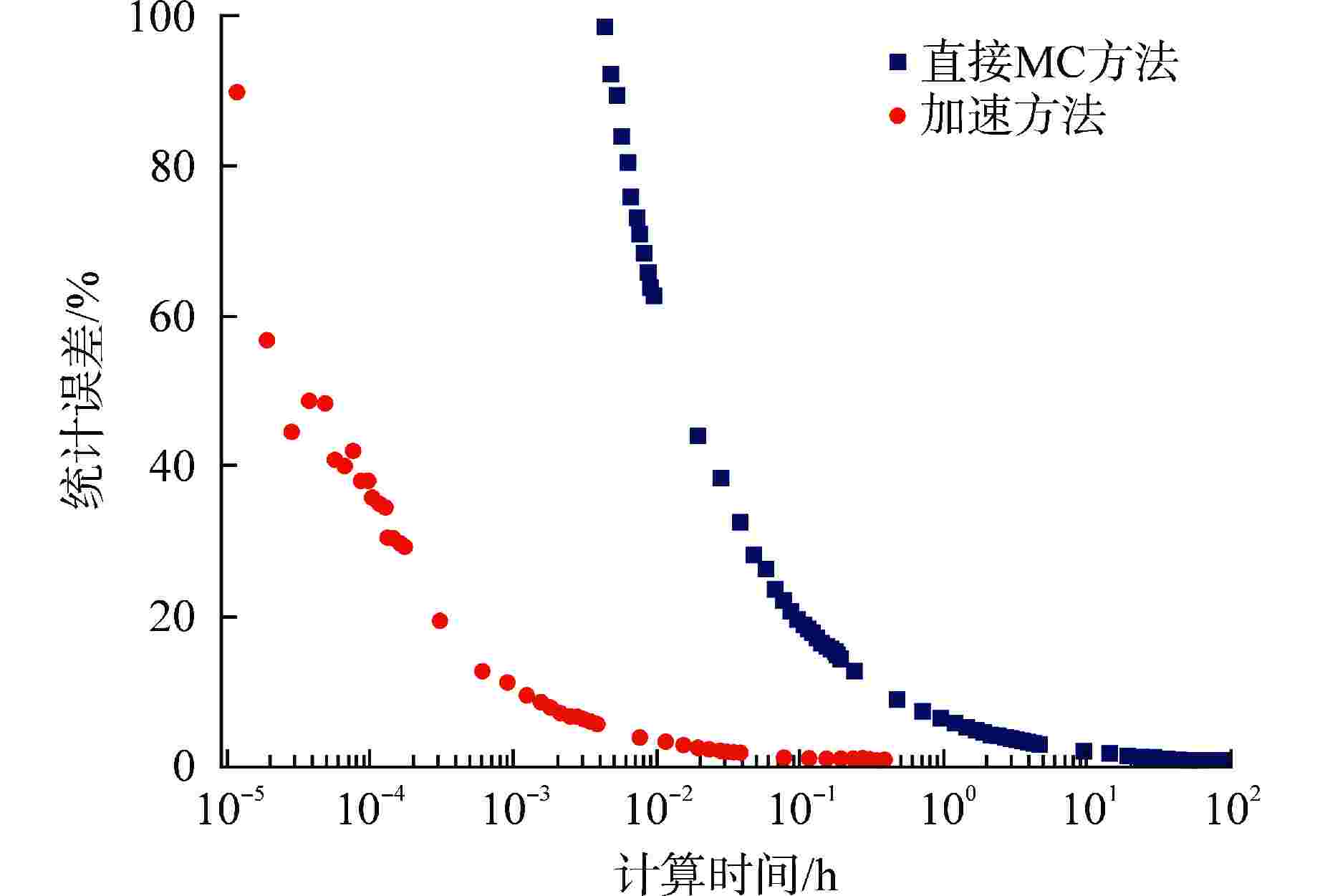
摘要: 为了改善传统压水堆辐照监督理论计算方法中需要多次物理建模和粒子输运计算及计算效率低的问题，本文基于蒙特卡罗（MC）方法和离散纵标（SN）方法耦合的正向权重一致共轭驱动重要性抽样（FW-CADIS）方法，建立了针对压力容器辐照监督管中子注量计算的加速方法。在某CPR1000机组中开展了计算精度和计算速度的影响因素研究，验证了该方法在不同堆芯参数下的适用性，给出了SN输运模拟参数的建议值；在某CPR1000机组中开展了验证与确认，结果表明，该方法与直接MC方法相比，中子注量率计算的品质因子（FOM）提高约95~181倍；中子注量计算结果与实测测量值的相对偏差不超过8%。因此，本文研究的辐照监督理论计算方法可以较好地提高该问题的计算效率，同时满足工程应用中的计算精度要求。
-
关键词:
- 中子注量 /
- 辐照监督 /
- 压水堆 /
- 正向权重一致共轭驱动重要性抽样（FW-CADIS） /
- 蒙特卡罗（MC）
Abstract: To address the inefficiency inherent in traditional pressurized water reactor irradiation surveillance theoretical calculation methods, which require multiple physical modeling and particle transport calculations, this study introduces an accelerated approach of neutron fluence calculation for pressure vessel irradiation surveillance capsules. The method is based on the Forward-Weighted Consistent Adjoint-Driven Importance Sampling (FW-CADIS) technique, coupling the Monte Carlo (MC) method with the Discrete Ordinates (SN) method. A comprehensive investigation into the influencing factors of computational accuracy and speed was conducted for a CPR1000 pressurized water reactor, validating the applicability of the proposed method under various core parameters and providing recommended values for SN transport simulation parameters. Verification and validation of the proposed method were performed on a CPR1000 pressurized water reactor. The results show that the Figure of Merit (FOM) of neutron fluence rate calculations is improved by approximately 95 to 181 times compared with the direct MC method, with a relative deviation between the calculated neutron fluence and measured values not exceeding 8%. Consequently, the irradiation surveillance theoretical calculation method presented in this study effectively enhances computational efficiency while meeting the precision requirements for engineering applications.-
Key words:
- Neutron fluence /
- Irradiation surveillance /
- Pressurized water reactor /
- FW-CADIS /
- Monte Carlo (MC)
-
图 1 辐照监督加速计算的实现过程
Figure 1. Flow Chart of the Acceleration of Irradiation Surveillance Calculation
图 3 不同角度离散数对收敛速度的影响
Figure 3. Influence of Different Angular Segmentation on Convergence Speed
图 4 不同空间离散尺寸对收敛速度的影响
Figure 4. Influence of Different Spatial Segmentation on Convergence Speed
图 5 直接MC方法与加速方法的收敛速度对比
Figure 5. Convergence Speed Comparison between Direct MC and Acceleration Method
表 1 堆芯参数敏感性分析
Table 1. Sensitivity Analysis of Reactor Core Parameters
参数类型 变化类型 统计误差/% 计算偏差/% 加速方法 直接MC方法 水密度变化 −0.2 g/cm3 0.52 1.04 0.53 −0.1 g/cm3 0.57 1.16 −0.56 0 g/cm3 0.62 1.30 −0.87 0.1 g/cm3 0.69 1.43 0.01 0.2 g/cm3 0.74 1.56 1.05 燃耗分布 第1循环 0.63 1.35 1.18 第2循环 0.63 1.36 1.90 第3循环 0.62 1.35 2.33 第4循环 0.62 1.35 2.54 功率分布 第1循环 0.62 1.30 −0.87 第2循环 0.64 1.33 −1.95 第3循环 0.63 1.29 0.32 第4循环 0.63 1.30 −0.48 能谱 第1循环 0.62 1.30 −0.87 第2循环 0.62 1.31 0.19 第3循环 0.62 1.29 −1.23 第4循环 0.62 1.28 −1.46 瓦特谱 0.63 1.31 −0.60 硼浓度变化 −200ppm 0.62 1.30 1.80 −100ppm 0.62 1.30 0.10 0ppm 0.62 1.30 −0.72 100ppm 0.62 1.29 0.21 200ppm 0.62 1.30 0.83 1ppm=10−6 
下载: 导出CSV
表 2 不同角度离散数对计算结果的影响
Table 2. Influence of Different Angular Segmentation on Calculation Results
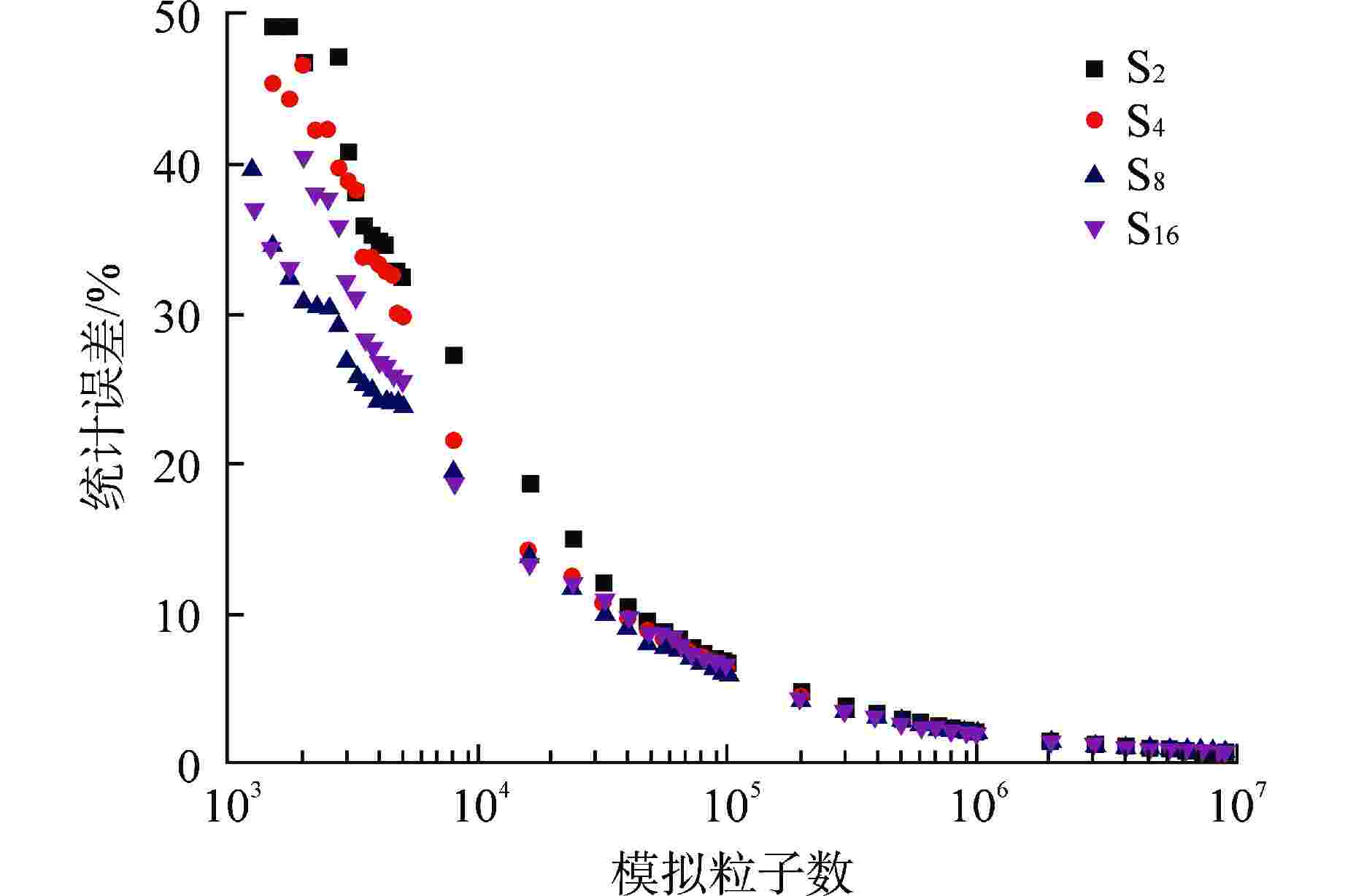
角度
离散数SN计算时间/s 模拟粒子数为105 模拟粒子数为107 统计误
差/%中子注量率
偏差/%统计误
差/%中子注量率
偏差/%S2 148 4.76 0.08 0.68 0.49 S4 279 4.49 0.51 0.64 −0.11 S8 718 4.14 −5.56 0.62 0.06 S16 2378 4.23 −3.89 0.63 −0.84
下载: 导出CSV
表 3 不同空间离散尺寸对计算结果的影响
Table 3. Influence of Different Spatial Segmentation on Calculation Results
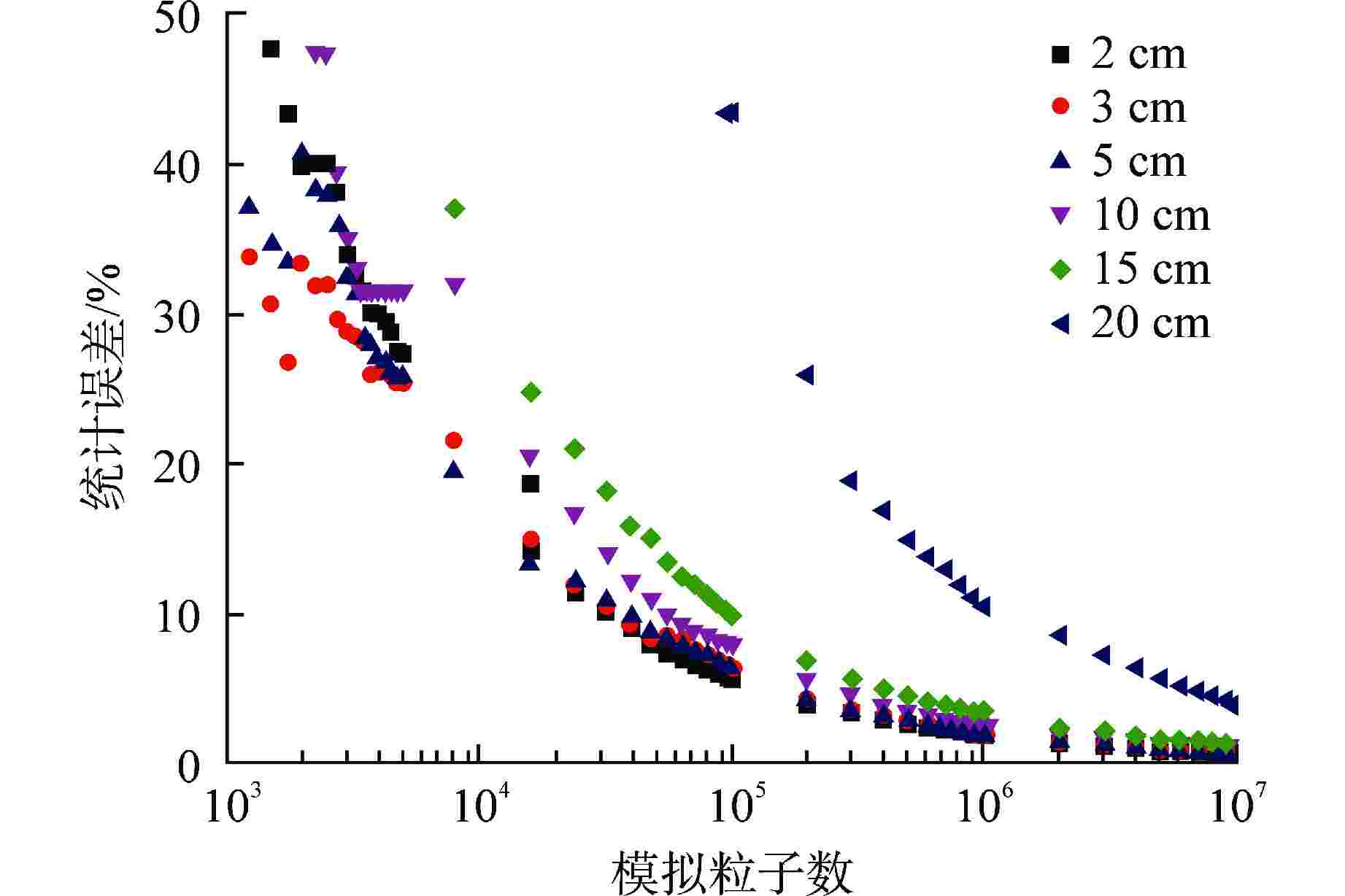
空间离散
尺寸/cm总网格数 SN计算时间/s 统计误差/% 中子注量率偏差/% 2 4.0×106 19789 0.60 0.38 3 1.2×106 7894 0.62 −0.34 5 2.2×105 2378 0.63 −0.84 10 2.8×104 2407 0.81 0.04 15 1.2×104 2388 1.17 −2.21 20 3.5×103 2841 3.87 −3.09
下载: 导出CSV
表 4 2种方法快中子注量理论计算值的对比
Table 4. Comparison of Theoretical Calculation Values of Fast Neutron Fluence using Two Methods
燃料循环 模拟方法 统计误
差/%计算时
间/hFOM 计算偏
差/%FOM比值 第1循环 直接MC方法 0.47 94.16 6.06 0.63 150 加速方法 0.60 0.38 907.68 第2循环 直接MC方法 0.34 133.86 8.27 1.28 113 加速方法 0.60 0.37 935.59 第3循环 直接MC方法 0.33 229.45 5.16 0.30 181 加速方法 0.60 0.37 932.42 第4循环 直接MC方法 0.46 67.20 8.72 0.90 95 加速方法 0.60 0.43 826.38
下载: 导出CSV
表 5 累积中子注量理论计算值与实测值的对比
Table 5. Comparison between Theoretical Calculated Values and Measured Values of Cumulative Neutron Fluence
探测器位置 能量范围 计算值与实测值偏差/% 直接MC方法 加速方法 上 E>1.0 MeV 6 5 E>0.1 MeV 2 1 中 E>1.0 MeV 6 8 E>0.1 MeV 3 4 下 E>1.0 MeV 8 6 E>0.1 MeV 7 7
下载: 导出CSV
-
[1] 能源行业核电标准化技术委员会. 轻水冷却反应堆压力容器辐照监督: NB/T 20220-2013[S]. 北京: 核工业标准化研究所,2013: 1-25. [2] 张斌,郑君萧,李晓静,等. 反应堆压力容器快中子注量计算不确定性分析[J]. 核技术,2018, 41(2): 020605. [3] 许怀金. RPV快中子注量率计算评估方法研究[D]. 北京: 华北电力大学(北京),2022. [4] 郑君萧. 基于SN方法的反应堆压力容器快中子注量率计算方法研究[D]. 北京: 华北电力大学(北京),2017. [5] 夏春梅,梅其良,丁谦学,等. DORT程序进行RPV中子注量率计算的可靠性验证[J]. 核科学与工程,2016, 36(3): 329-334. doi: 10.3969/j.issn.0258-0918.2016.03.005 [6] VASILIEV A, FERROUKHI H, ZIMMERMANN M A, et al. Development of a CASMO-4/SIMULATE-3/MCNPX calculation scheme for PWR fast neutron fluence analysis and validation against RPV scraping test data[J]. Annals of Nuclear Energy, 2007, 34(8): 615-627. doi: 10.1016/j.anucene.2007.02.020 [7] 靳忠敏,陈义学,石生春,等. 基于MCNP的压力容器快中子注量率计算参数敏感性分析[J]. 原子能科学技术,2011, 45(2): 195-199. [8] 石秀安,苏耿华,包鹏飞. 压水堆辐照监督管中子注量计算方法改进研究[J]. 核科学与工程,2018, 38(4): 585-589. doi: 10.3969/j.issn.0258-0918.2018.04.008 [9] 邓理邻,吕焕文,谭怡,等. 辐照监督管中子注量率精细化模型计算方法研究[J]. 核动力工程,2013, 34(S1): 84-86. [10] 刘巧凤,韩静茹. CAP1400反应堆压力容器快中子注量独立审核计算[J]. 中国核电,2018, 11(4): 462-465. [11] TIEP N H, HOANG S M T, HARTANTO D, et al. Investigation of the VVER-1000 reactor pressure vessel neutron fluence and displacement per atom using MCNP6[J]. Radiation Physics and Chemistry, 2020, 177: 109141. doi: 10.1016/j.radphyschem.2020.109141 [12] NGUYEN H T, NHU V H P, NGUYEN M T. Calculation of neutron and gamma fluences on VVER reactor pressure vessel[J]. Nuclear Science and Technology, 2016, 6(4): 18-25. doi: 10.53747/jnst.v6i4.172 [13] ARDEKANI S F G, HADAD K. Monte Carlo evaluation of neutron irradiation damage to the VVER-1000 RPV[J]. Nuclear Energy and Technology, 2017, 3(2): 73-80. doi: 10.1016/j.nucet.2017.04.001 [14] 李刚,张宝印,邓力,等. 蒙特卡罗粒子输运程序JMCT研制[J]. 强激光与粒子束,2013, 25(1): 158-162. [15] YANG C, CHENG T P, DENG L, et al. Development of 3-D parallel first-collision source method for discrete ordinate code JSNT-S[J]. Annals of Nuclear Energy, 2020, 135: 106942. doi: 10.1016/j.anucene.2019.106942 [16] 邓力,李刚,张宝印,等. JMCT蒙特卡罗中子-光子输运程序全堆芯pin-by-pin模型的模拟[J]. 原子能科学技术,2014, 48(6): 1061-1066. doi: 10.7538/yzk.2014.48.06.1061 [17] 邓力,李瑞,丁谦学,等. 基于JMCT秦山核电厂一期反应堆屏蔽计算与分析[J]. 核动力工程,2021, 42(2): 173-179. [18] 李刚,邓力,张宝印,等. BEAVRS基准模型热零功率状态的JMCT分析[J]. 物理学报,2016, 65(5): 052801. doi: 10.7498/aps.65.052801 [19] 刘雄国,邓力,胡泽华,等. 基于VENUS-Ⅲ国际基准模型的JMCT程序验证[J]. 计算物理,2016, 33(5): 570-580. [20] 杨超,程汤培,邓力,等. 三维并行程序JSNT对HBR-2装置的屏蔽计算与分析[J]. 原子能科学技术,2019, 53(2): 250-255. [21] 张广春,程汤培,邓力,等. 基于JSNT程序的压水堆屏蔽计算[J]. 强激光与粒子束,2017, 29(3): 036020. [22] 史涛. 蒙特卡罗粒子输运问题中的减方差方法研究[D]. 绵阳: 中国工程物理研究院,2018. [23] 王超,邓力. 基于MCNP多群伴随计算与正算分析的比较[J]. 原子核物理评论,2012, 29(4): 388-394. [24] WAGNER C J, PEPLOW E D, MOSHER W S. FW-CADIS method for global and regional variance reduction of Monte Carlo radiation transport calculations[J]. Nuclear Science and Engineering, 2014, 176(1): 37-57. doi: 10.13182/NSE12-33 -
计量
- 文章访问数: 28
- HTML全文浏览量: 5
- PDF下载量: 3
- 被引次数: 0
