Research on Nuclear Data Target Accuracy Assessment Based on Subspace Method
-
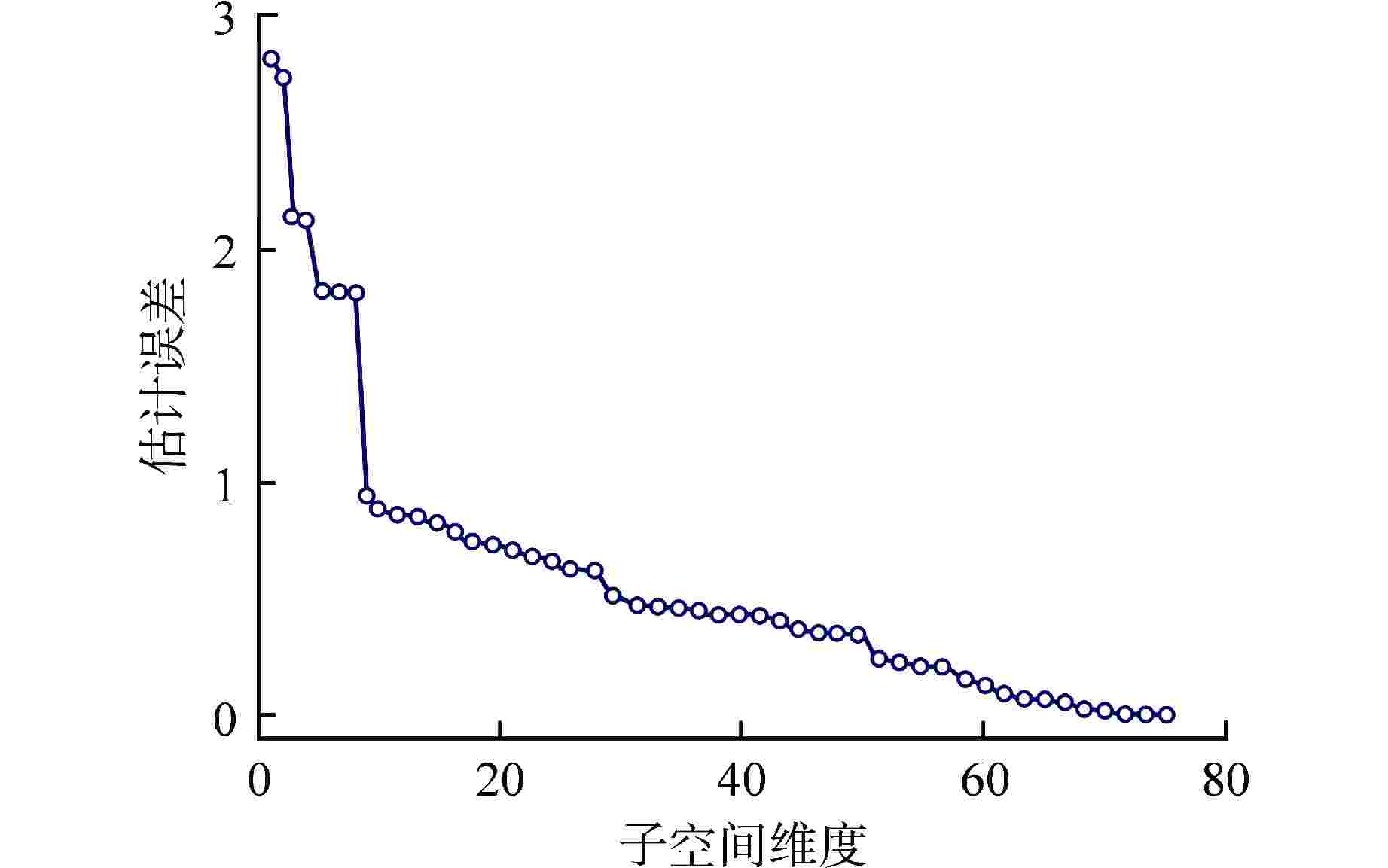
摘要: 核数据目标精度评估根据反应堆物理计算响应函数的目标不确定度限制，反向求出核数据的不确定度水平要求，对于引导核数据的研究方向、提升反应堆的经济性和安全性有重要意义。目标精度评估的数学形式是一个非线性规划问题，参与运算的核数据数量庞大，难以在全维度空间内求解。子空间方法是一种有效的特殊降维方法，该方法通过矩阵变换，可以在尽量保留高维信息的前提下，将高维问题转化为低维问题，提高数值计算的稳定性。基于子空间方法的ZPPR-9核数据目标精度评估研究结果表明，对于有效增殖因数目标精度为0.3%的不确定度要求，计算维度可由1170维降低到71维。本研究建立的数值方法能够用于目标精度评估计算。Abstract: According to the target uncertainty limit of reactor physics response calculation, target accuracy assessment solves a problem which identifies the demands for nuclear data uncertainties, which is of great significance for guiding the research direction of nuclear data and improving the economy and safety of reactors. Target accuracy assessment is a nonlinear constrained optimization problem in mathematics. Due to the ultra-large amount of nuclear data, solving the optimization problem in full-space is impossible. Subspace method is an efficient dimensionality reduction method. Through matrix transformation defined by subspace, a high-dimensional problem can be transformed into a low-dimensional problem, while the high-dimensional information is mostly retained, and the stability of numerical calculation is enhanced. Research on ZPPR-9 nuclear data target accuracy assessment based on subspace method shows that, with the 0.3% target uncertainty limit of effective multiplication factor, computational dimension can be reduced from 1170 to 71. The numerical method presented in this paper can be used in future target accuracy assessment calculations.
-
Key words:
- Uncertainty /
- Nuclear data /
- Target accuracy assessment /
- Subspace
-
图 4 238U非弹性散射截面分群灵敏度及不确定度
Figure 4. Sensitivity and Uncertainty of 238U Inelastic Cross Section
图 6 估计误差随子空间维度变化关系
Figure 6. Relationship between Estimation Error and Subspace Dimension
表 1 快堆主要参数目标精度
Table 1. Target Accuracies of Fast Reactor Major Parameters
参数名 目标精度 keff（寿期初）/pcm 300 功率峰因子（寿期初）/% 2 燃耗反应性损失/pcm 300 反应性系数（寿期初）/% 7 辐照周期末主要核素核子密度/% 2 辐照周期末其他核素核子密度/% 10 1pcm=10−5 
下载: 导出CSV
表 2 各核素考虑反应道及计算不确定度
Table 2. Nuclear Reaction of Nuclei and Uncertainty Results
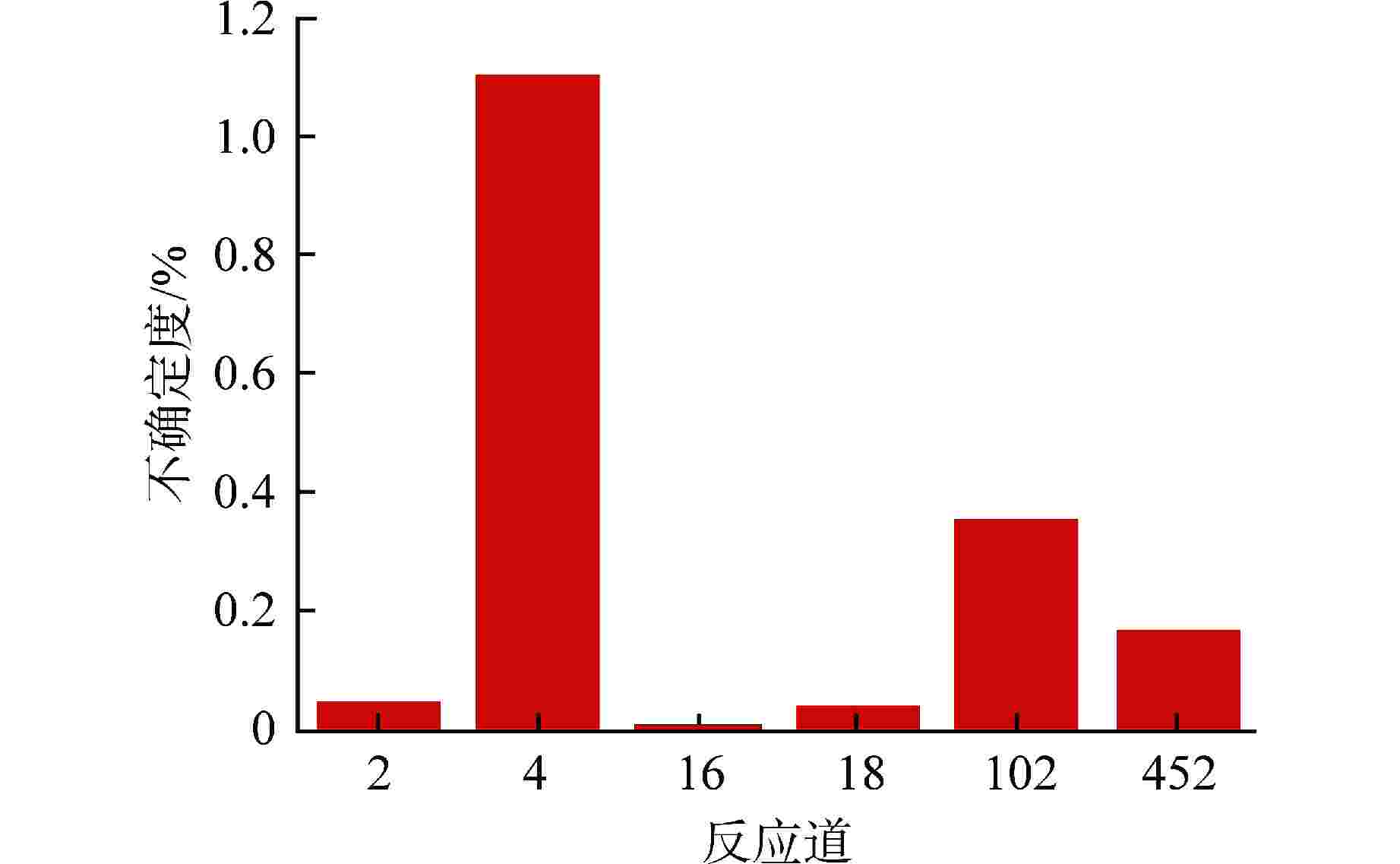
核素 反应道（MT） 不确定度/% 235U 2, 4, 16, 18, 102, 452 0.03 238U 2, 4, 16, 18, 102, 452 1.21 239Pu 2, 4, 16, 18, 102, 452 0.39 240Pu 2, 4, 16, 18, 102, 452 0.04 241Pu 2, 4, 16, 18, 102, 452 0.01 16O 2, 4, 102 0.04 23Na 2, 4, 102 0.11 52Cr 2, 4, 102 0.02 56Fe 2, 4, 102 0.15 58Ni 2, 4, 102 0.02
下载: 导出CSV
表 3 子空间方法目标精度评估结果
Table 3. Target Accuracy Assessment Results Based on Subspace Method
核素 反应道（MT） 能量区间/eV 原始
不确定度/%目标
不确定度/%238U 4 [1.35×106,2.23×106] 20.58 2.09 238U 4 [2.23×106,3.68×106] 19.42 2.06 238U 4 [3.68×106,6.07×106] 20.14 2.9 238U 4 [8.21×105,1.35×106] 16.94 2.89 238U 4 [6.07×106,1.00×107] 30.3 7.02 239Pu 102 [5.53×103,9.12×103] 16.54 4.26 239Pu 102 [3.35×103,5.53×103] 16.54 4.81 238U 2 [1.35×106,2.23×106] 18.78 5.97 239Pu 4 [4.98×105,8.21×105] 32.61 10.93 23Na 4 [4.98×105,8.21×105] 17.54 6.02 238U 4 [6.74×104,1.11×105] 19.18 6.66 238U 18 [5.53×103,9.12×103] 408.03 142.12 56Fe 4 [1.35×106,2.23×106] 11.98 4.4 239Pu 102 [2.03×103,3.35×103] 10.73 4 239Pu 4 [1.11×105,1.83×105] 43.73 16.36 239Pu 4 [6.74×104,1.11×105] 50 20.06 56Fe 102 [4.98×105,8.21×105] 25.24 10.48 239Pu 102 [4.09×104,6.74×104] 11.4 4.79 238U 2 [2.23×106,3.68×106] 15.25 6.55 239Pu 4 [3.02×105,4.98×105] 32.71 14.15
下载: 导出CSV
表 4 直接筛选法目标精度评估结果
Table 4. Target Accuracy Assessment Results Based on Direct Screening Method
核素 反应道（MT） 能量区间/eV 原始
不确定度/%目标
不确定度/%238U 4 [1.35×106,2.23×106] 20.58 0.98 238U 4 [2.23×106,3.68×106] 19.42 0.96 238U 2 [1.35×106,2.23×106] 18.78 1.08 238U 4 [3.68×106,6.07×106] 20.14 1.35 238U 2 [2.23×106,3.68×106] 15.25 1.18 238U 4 [8.21×105,1.35×106] 16.94 1.34 238U 2 [8.21×105,1.35×106] 9.32 0.93 238U 4 [6.07×106,1.00×107] 30.3 3.26 239Pu 102 [5.53×103,9.12×103] 16.54 1.94 238U 2 [3.68×106,6.07×106] 13.19 1.66 238U 4 [6.74×104,1.11×105] 19.18 2.52 239Pu 102 [3.35×103,5.53×103] 16.54 2.18 238U 18 [5.53×103,9.12×103] 408.03 54.04 239Pu 4 [4.98×105,8.21×105] 32.61 4.78 23Na 4 [4.98×105,8.21×105] 17.54 2.6 56Fe 102 [4.98×105,8.21×105] 25.24 4.13 56Fe 4 [1.35×106,2.23×106] 11.98 1.98 239Pu 4 [1.11×105,1.83×105] 43.73 7.24 239Pu 102 [2.03×103,3.35×103] 10.73 1.82 56Fe 102 [3.02×105,4.98×105] 25.2 4.42
下载: 导出CSV
-
[1] 汤涛,周涛. 不确定性量化的高精度数值方法和理论[J]. 中国科学: 数学,2015, 45(7): 891-928. [2] SULLIVAN T J. Introduction to uncertainty quantification[M]. Cham: Springer, 2015: 1-6. [3] SALVATORES M, JACQMIN R. International evaluation co-operation volume 26: Uncertainty and target accuracy assessment for innovative systems using recent covariance data evaluations[R]. Vienna: OECD/NEA, 2008. [4] ALIBERTI G, PALMIOTTI G, SALVATORES M, et al. Nuclear data sensitivity, uncertainty and target accuracy assessment for future nuclear systems[J]. Annals of Nuclear Energy, 2006, 33(8): 700-733. doi: 10.1016/j.anucene.2006.02.003 [5] USACHEV L N, BOBKOV Y G. Planning an optimum set of microscopic experiments and evaluation to obtain a given accuracy in reactor parameter calculations: INDC(CCP)-19/U[R]. Vienna: INDC, 1972. [6] 刘勇,曹良志,吴宏春,等. 核数据敏感性与不确定性分析及其在目标精度评估中的应用[J]. 原子能科学技术,2019, 53(1): 86-93. doi: 10.7538/yzk.2018.youxian.0136 [7] 朱帅涛. 快能谱反应堆多群核数据的调整与精度评估方法研究[D]. 北京: 华北电力大学(北京),2020. [8] DENSMORE J D, MCKINNEY G W, HENDRICKS J S. Correction to the MCNP perturbation feature for cross-section dependent tallies: LA-13374[R]. Los Alamos, New Mexico: Los Alamos National Laboratory, 1997. [9] KIEDROWSKI B C. MCNP6.1 k-eigenvalue sensitivity capability: a user’s guide: LA-UR-13-22251[R]. Los Alamos: Los Alamos National Laboratory, 2013. [10] MACFARLANE R, MUIR D W, BOICOURT R M, et al. The NJOY nuclear data processing system, version 2016: LA-UR-17-20093[R]. Los Alamos: Los Alamos National Laboratory, 2017. [11] RUSSI T M. Uncertainty quantification with experimental data and complex system models[D]. Berkeley: University of California, Berkeley, 2010. [12] CONSTANTINE P G, DOW E, WANG Q Q. Active subspace methods in theory and practice: applications to Kriging surfaces[J]. SIAM Journal on Scientific Computing, 2014, 36(4): A1500-A1524. doi: 10.1137/130916138 [13] ABDEL-KHALIK H S. Adaptive core simulation[D]. Raleigh: North Carolina State University, 2004. [14] CONSTANTINE P G. Active subspaces: emerging ideas for dimension reduction in parameter studies[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2015: 21-44. [15] HU X Z, CHEN X Q, ZHAO Y, et al. Active subspace approach to reliability and safety assessments of small satellite separation[J]. Acta Astronautica, 2017, 131: 159-165. doi: 10.1016/j.actaastro.2016.10.042 [16] LI J C, CAI J S, QU K. Surrogate-based aerodynamic shape optimization with the active subspace method[J]. Structural and Multidisciplinary Optimization, 2019, 59(2): 403-419. doi: 10.1007/s00158-018-2073-5 [17] ABDEL-KHALIK H S, BANG Y, WANG C J. Overview of hybrid subspace methods for uncertainty quantification, sensitivity analysis[J]. Annals of Nuclear Energy, 2013, 52: 28-46. doi: 10.1016/j.anucene.2012.07.020 [18] LEWIS A, SMITH R, WILLIAMS B. Gradient free active subspace construction using Morris screening elementary effects[J]. Computers & Mathematics with Applications, 2016, 72(6): 1603-1615. [19] KHUWAILEH B A, ABDEL-KHALIK H S. Subspace-based inverse uncertainty quantification for nuclear data assessment[J]. Nuclear Data Sheets, 2015, 123: 57-61. doi: 10.1016/j.nds.2014.12.010 [20] HALKO N, MARTINSSON P G, TROPP J A. Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions[J]. SIAM Review, 2011, 53(2): 217-288. doi: 10.1137/090771806 [21] LUO W, LI B. Combining eigenvalues and variation of eigenvectors for order determination[J]. Biometrika, 2016, 103(4): 875-887. doi: 10.1093/biomet/asw051 [22] JOLLIFFE I T. Principal component analysis[M]. 2nd ed. New York: Springer, 2002: 10-28. [23] ISHIKAWA M, IKEGAMI T, SANDA T. ZPPR benchmarks for large LMFBR core physics from JUPITER cooperative program between United States and Japan[J]. Nuclear Science and Engineering, 2014, 178(3): 335-349. doi: 10.13182/NSE14-9 [24] IWAI T, SUGINO K, ISHIKAWA M. Development of the ZPPR-9 core benchmark problem: PNC TN9410 98-079[R]. Japan: Power Reactor and Nuclear Fuel Development Corporation, 1998. [25] SALVATORES M, PALMIOTTI G, ALIBERTI G, et al. Methods and issues for the combined use of integral experiments and covariance data: NEA-NSC-WPEC-DOC-2013-445[R]. Vienna: OECD/NEA, 2013. [26] TADA K, YAMAMOTO A, KUNIEDA S, et al. Nuclear data processing code FRENDY version 2: JAEA-Data/Code 2022-009[R]. Japan: Japan Atomic Energy Agency, 2023. -
图(6) / 表(4)
计量
- 文章访问数: 19
- HTML全文浏览量: 3
- PDF下载量: 1
- 被引次数: 0
