SST k-ω-γ模型修正及其对螺旋管内层流向湍流转捩过程的预测

蔡昀彤; 赵后剑; 李晓伟; 苏阳; 鹿一鸣; 郭张鹏; 刘芳

doi:10.13832/j.jnpe.2024.06.0055

SST k-ω-γ模型修正及其对螺旋管内层流向湍流转捩过程的预测

doi: 10.13832/j.jnpe.2024.06.0055

1.
华北电力大学核科学与工程学院，北京，102206
2.
清华大学核能与新能源技术研究院，北京，100084

基金项目: 国家重点研发计划资助项目（2022YFB1902503）；国家自然科学基金面上项目（12275084）

详细信息

作者简介:
蔡昀彤（2002—），女，硕士研究生，现主要从事螺旋管管内流动换热方面研究，E-mail: yuntongcai@ncepu.edu.cn

通讯作者:
赵后剑，E-mail: zhaohoujian@ncepu.edu.cn

中图分类号: TK124；TL334
计量
- 文章访问数: 16
- HTML全文浏览量: 4
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2023-12-18
- 修回日期: 2024-10-09
- 刊出日期: 2024-12-17

Modified SST k-ω-γ Model and Prediction of Laminar to Turbulent Flow Transition in Helical Tube

1.
School of Nuclear Science and Engineering, North China Electric Power University, Beijing, 102206, China
2.
Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing, 100084, China

摘要

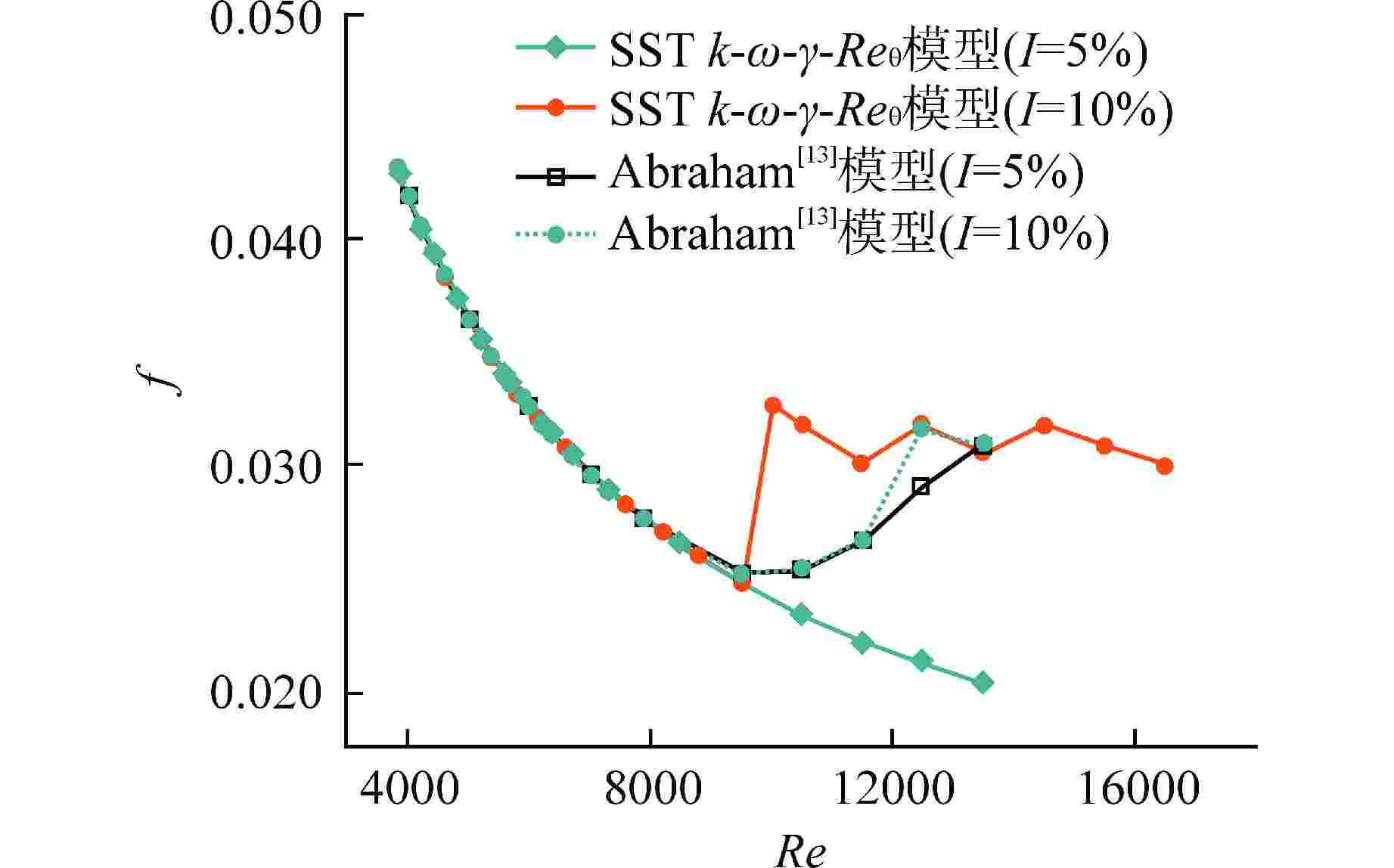
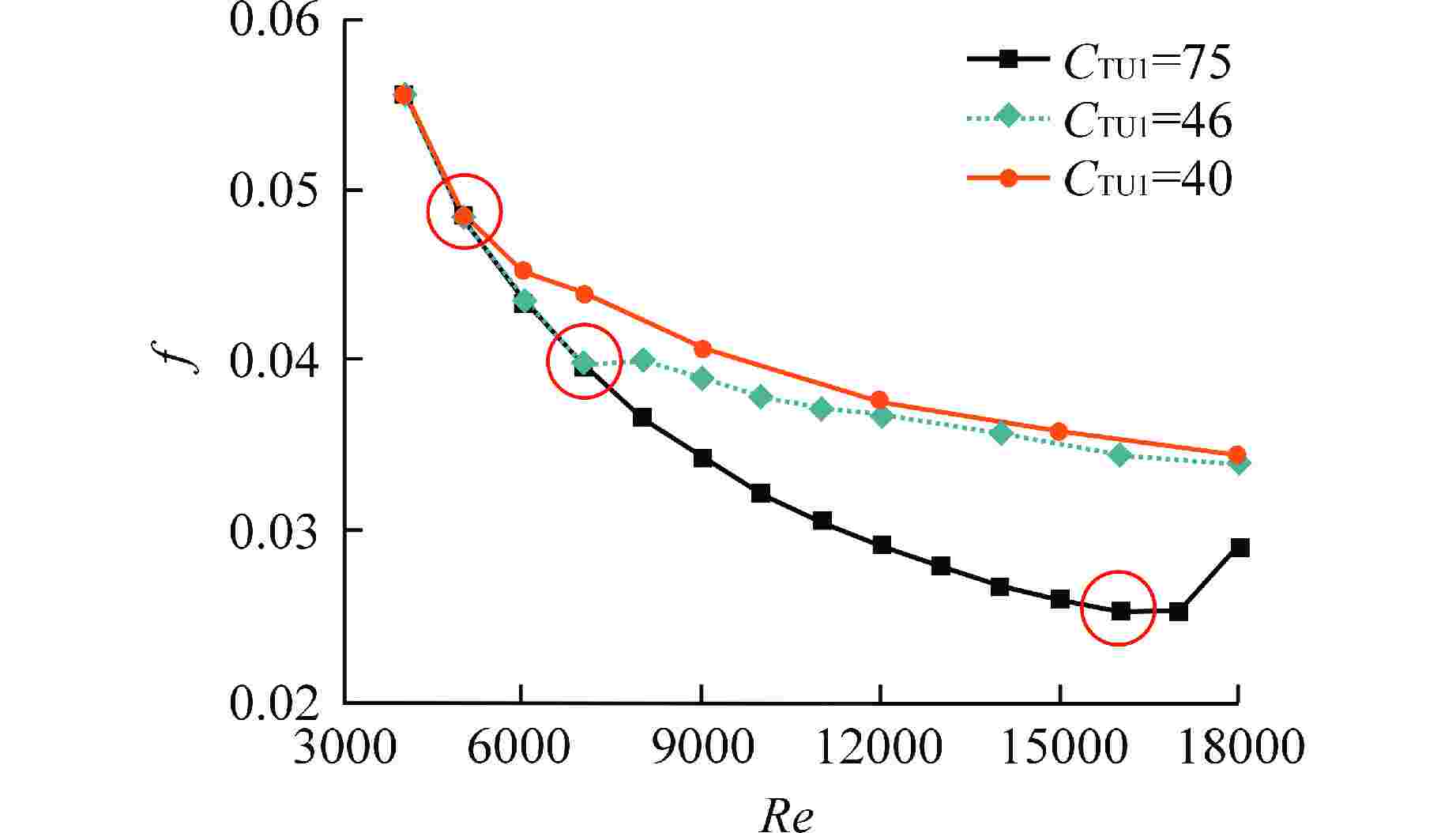
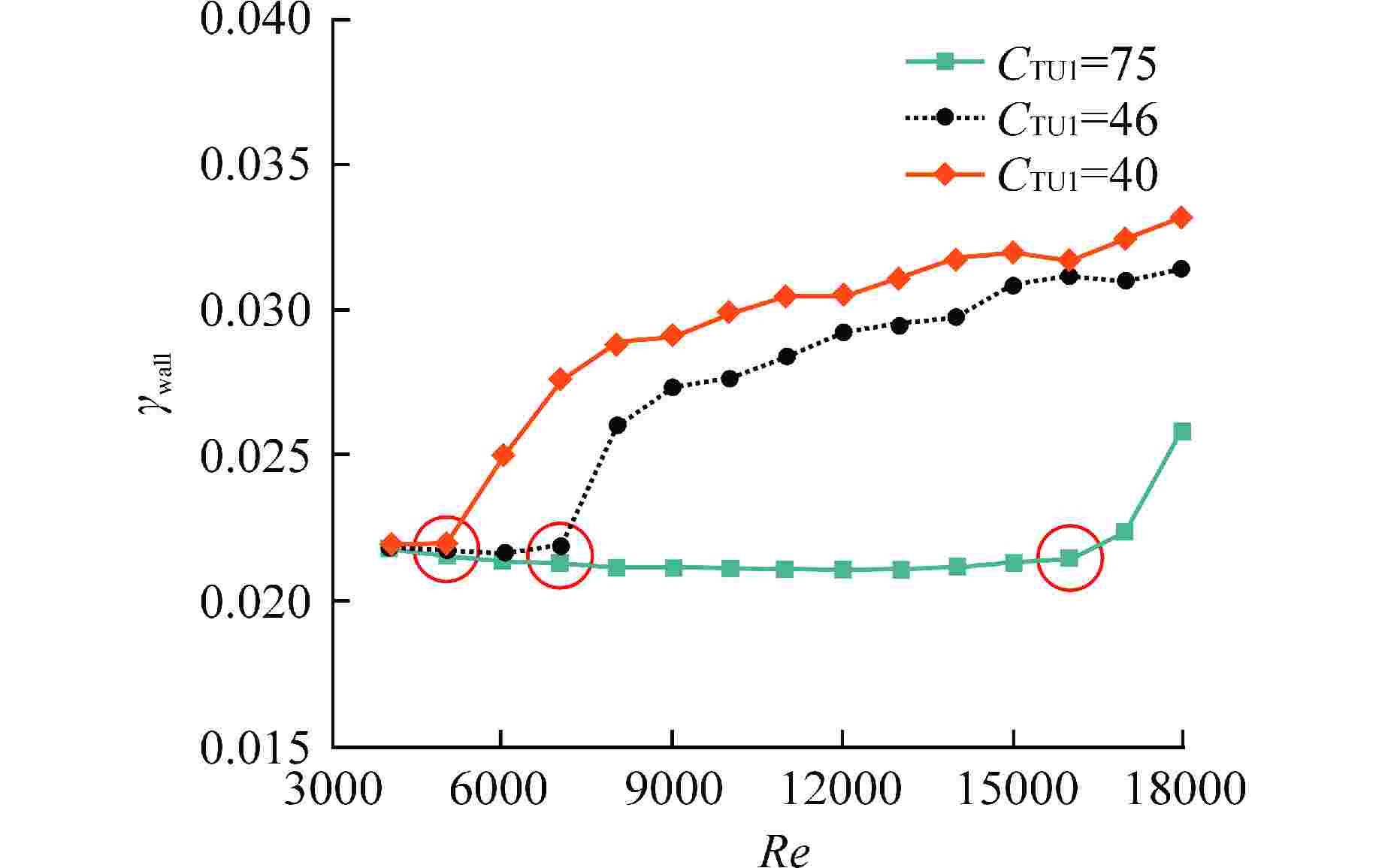
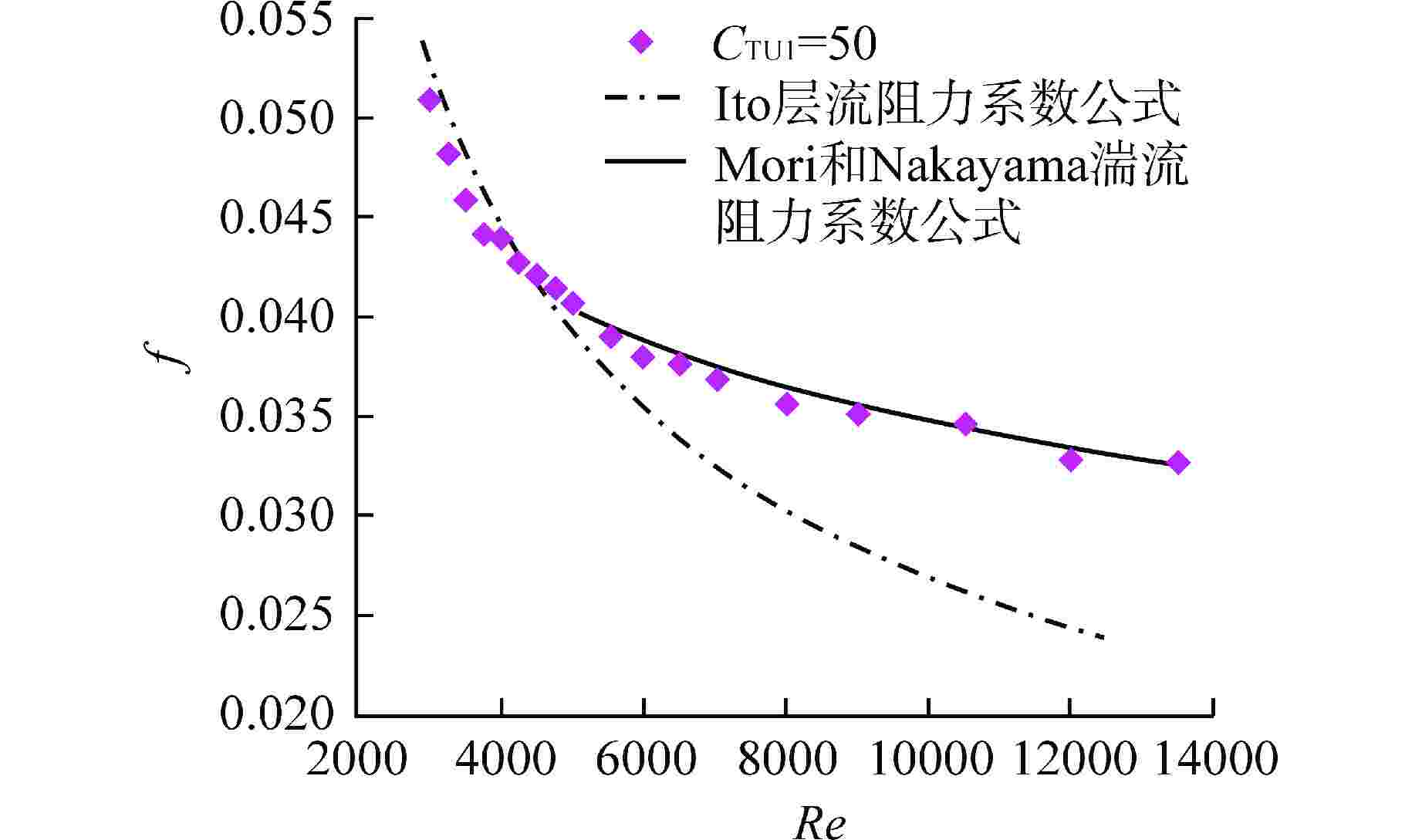
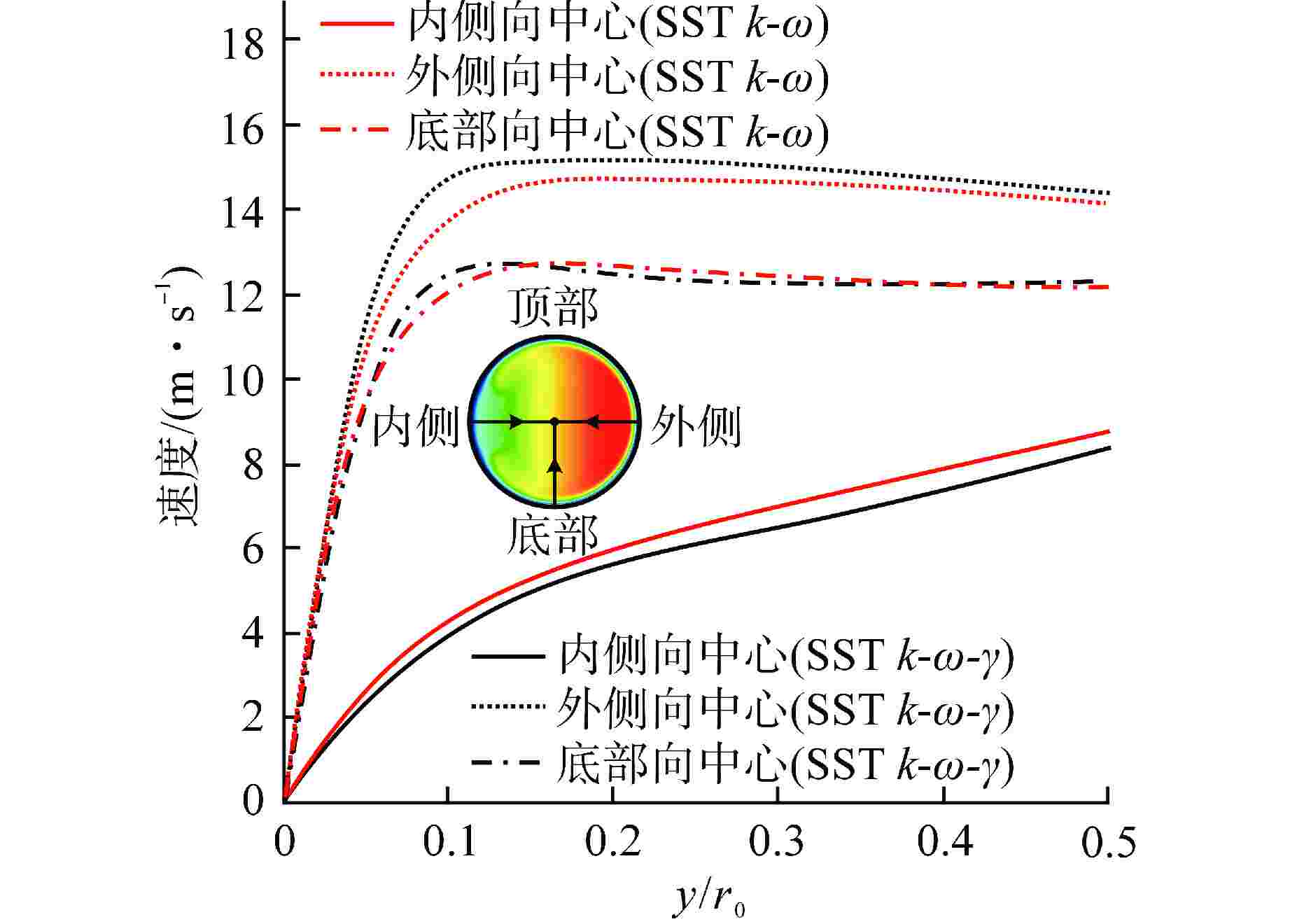
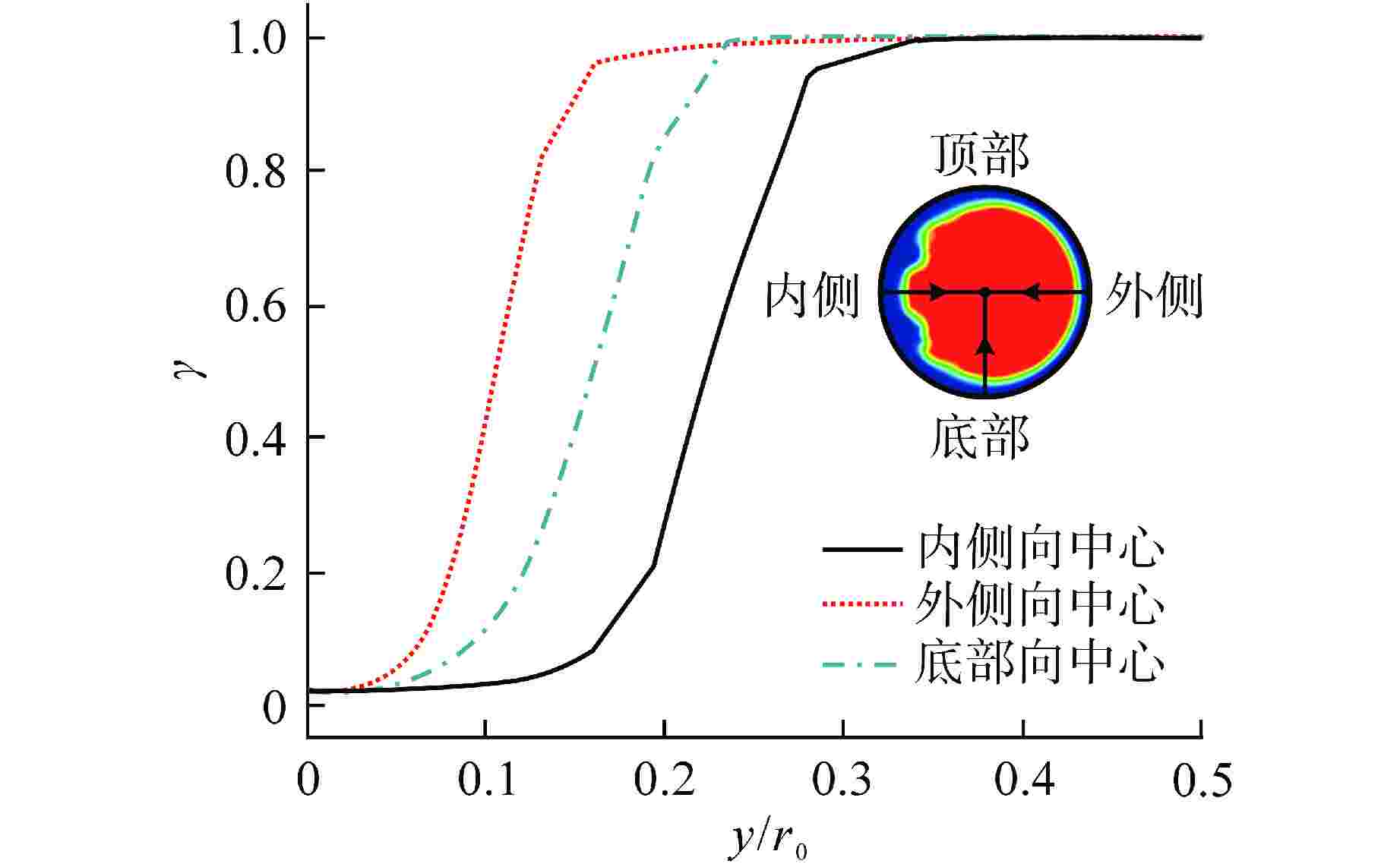
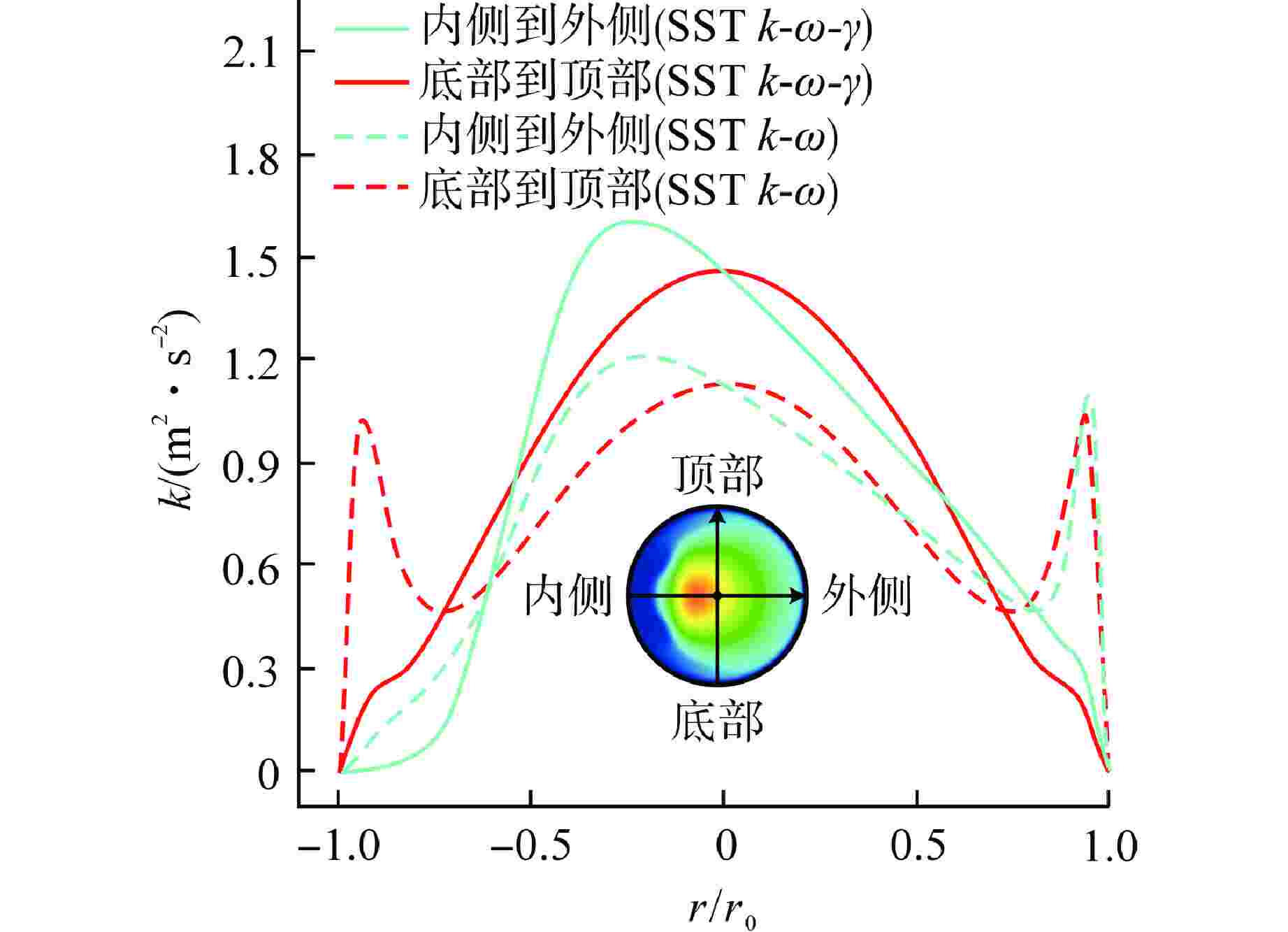
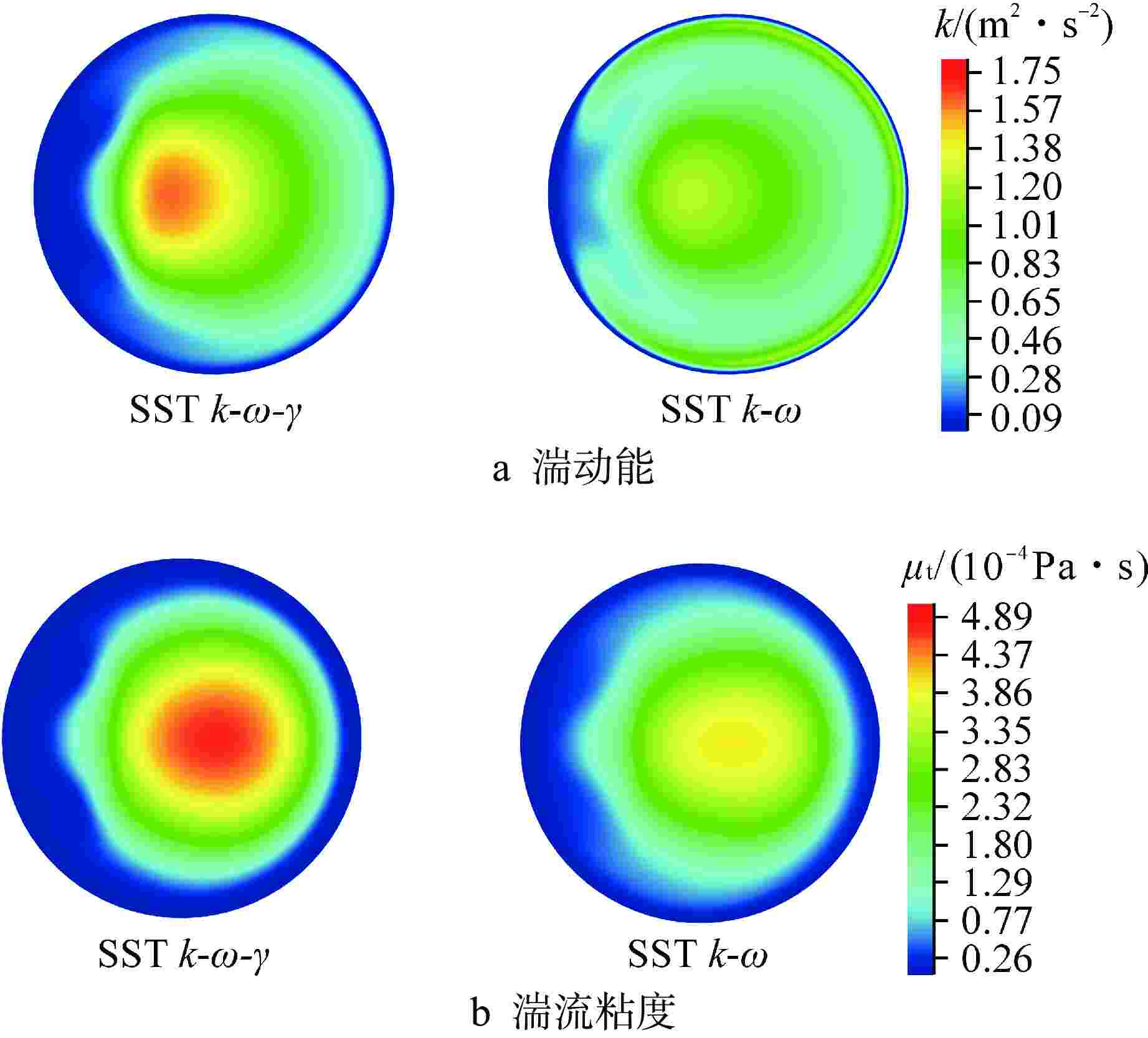
摘要: 螺旋管式换热器因具有结构紧凑和换热性能好等优点，在各领域被广泛应用。区别于直管内流动，流体在螺旋管内流动时会受到离心力作用。由于离心力的存在，螺旋管内层流向湍流转捩的临界雷诺数会随着螺旋曲率的增大而增大。本文采用数值方法研究了螺旋管内层流向湍流的转捩过程，通过分析阻力系数随雷诺数的变化关系，对比剪切应力输运（SST） k-ω-γ-Re_θ模型和SST k-ω-γ模型模拟转捩过程的准确性，分析了不同入口湍流强度（5%、10%）对计算结果的影响。SST k-ω-γ-Re_θ模型对入口湍流强度较敏感，而SST k-ω-γ模型受入口湍流强度影响较小。与前人经验关系式相比，SST k-ω-γ模型模拟得到的临界雷诺数偏大。本文通过调节SST k-ω-γ模型中γ输运方程的经验系数，发现经验系数C_TU1对转捩起始点有较大影响，同一曲率下，临界雷诺数随C_TU1增大而增大。本文基于现有经验公式确定了不同曲率螺旋管（0.02、0.04、0.06、0.11）所对应的C_TU1，并拟合得到螺旋曲率和C_TU1的关联式，验证了修正后SST k-ω-γ模型模拟螺旋管内层流和湍流阻力系数的准确性，比较了SST k-ω模型和修正SST k-ω-γ模型计算结果中速度、湍动能以及湍流粘度等变量的不同。
- 螺旋管 /
- 阻力系数 /
- 层流 /
- 湍流 /
- 转捩
Abstract: Helical tube heat exchangers are widely used in various fields due to compactness and good heat transfer performance. Different from the flow in a straight pipe, the fluid will be subjected to centrifugal force when flowing in a helical tube. Due to the existence of centrifugal force, the critical Reynolds number for the transition from laminar to turbulent flow in the helical tube increases with the increasing of helical curvature ratios. In the current investigation, the transition process from laminar to turbulent flow in the helical tube is studied by numerical method. By analyzing the relationship between the resistance coefficient and Reynolds number, the accuracy of simulating the transition process by the shear stress transport (SST) k-ω-γ-Re_θ model and SST k-ω-γ model is compared, and the effects of different inlet turbulence intensities (5% and 10%) on the calculation results are analyzed. The SST k-ω-γ-Re_θ model is more sensitive to inlet turbulent intensities, while the SST k-ω-γ model is less affected by inlet turbulent intensities. The critical Reynolds number obtained by SST k-ω-γ model is larger than the critical Reynolds number calculated by the empirical correlation in the literature. In this paper, by adjusting the empirical coefficient of γ transport equation in SST k-ω-γ model, it is found that C_TU1 has a significant influence on the onset of the transition process. With the same helical curvature ratio, the critical Reynolds number increases with the increasing of C_TU1. In the current investigation, based on the existing empirical formula, the C_TU1 for different helical curvature ratios (δ=0.02, 0.04, 0.06, and 0.11) are determined, and the correlation between helical curvature and C_TU1 is obtained by fitting. The accuracy of the modified SST k-ω-γ model in simulating the laminar and turbulent friction factors in helical tubes is verified, and the differences of velocity, turbulent kinetic energy and turbulent viscosity in the calculation results of SST k-ω model and modified SST k-ω-γ model are compared.
- Helical tube /
- Friction factor /
- Laminar flow /
- Turbulent flow /
- Transition

HTML全文

图 1 螺旋管结构示意图

Figure 1. Schematic Diagram of Helical Tube Structure

下载: 全尺寸图片幻灯片

图 2 不同入口湍流强度时的阻力系数

Figure 2. Friction Factors with Different Inlet Turbulent Intensities

下载: 全尺寸图片幻灯片

图 3 不同C_TU1对阻力系数的影响

Figure 3. Friction Factors with Different C_TU1

下载: 全尺寸图片幻灯片

图 4 不同C_TU1对γ_wall的影响

Figure 4. γ_wall with Different C_TU1

下载: 全尺寸图片幻灯片

图 5 δ=0.02时阻力系数随雷诺数的变化

Figure 5. Variation of Friction Factor with Reynolds Number (δ=0.02)

下载: 全尺寸图片幻灯片

图 6 δ=0.11时阻力系数随雷诺数的变化

Figure 6. Variation of Friction Factor with Reynolds Number (δ=0.11)

下载: 全尺寸图片幻灯片

图 7 修正SST k-ω-γ模型的阻力系数结果

Figure 7. Friction Factors with Modified SST k-ω-γ Model

下载: 全尺寸图片幻灯片

图 8 不同湍流模型所计算的阻力系数

Figure 8. Friction Factors Calculated by Different Turbulent Models

下载: 全尺寸图片幻灯片

图 9 周向切应力分布

Figure 9. Wall Shear Stress Distributions

下载: 全尺寸图片幻灯片

图 10 δ=0.11、Re=6000时截面内速度分布

Figure 10. Velocity Distribution in Cross Section when δ=0.11 and Re=6000

下载: 全尺寸图片幻灯片

图 11 δ=0.11、Re=6000时截面内湍流间歇性分布

Figure 11. Turbulent Intermittency Distribution in Cross Section when δ=0.11 and Re=6000

下载: 全尺寸图片幻灯片

图 12 δ=0.11、Re=6000时截面内湍动能分布

Figure 12. Turbulent Kinetic Energy Distribution in Cross Section when δ=0.11 and Re=6000

下载: 全尺寸图片幻灯片

图 13 湍动能和湍流粘度云图

Figure 13. Contour of Turbulent Kinetic Energy and Turbulent Viscosity

下载: 全尺寸图片幻灯片

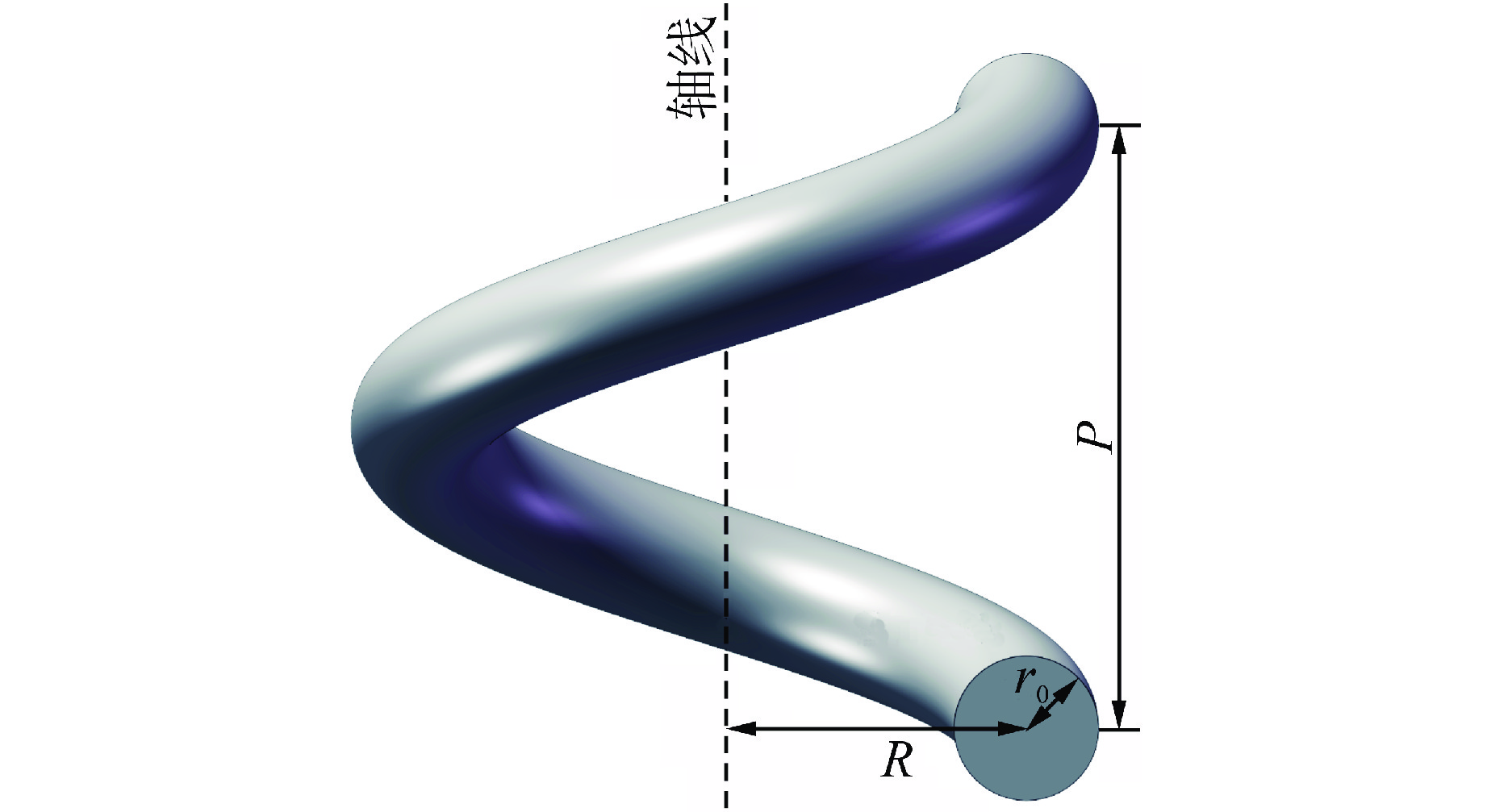
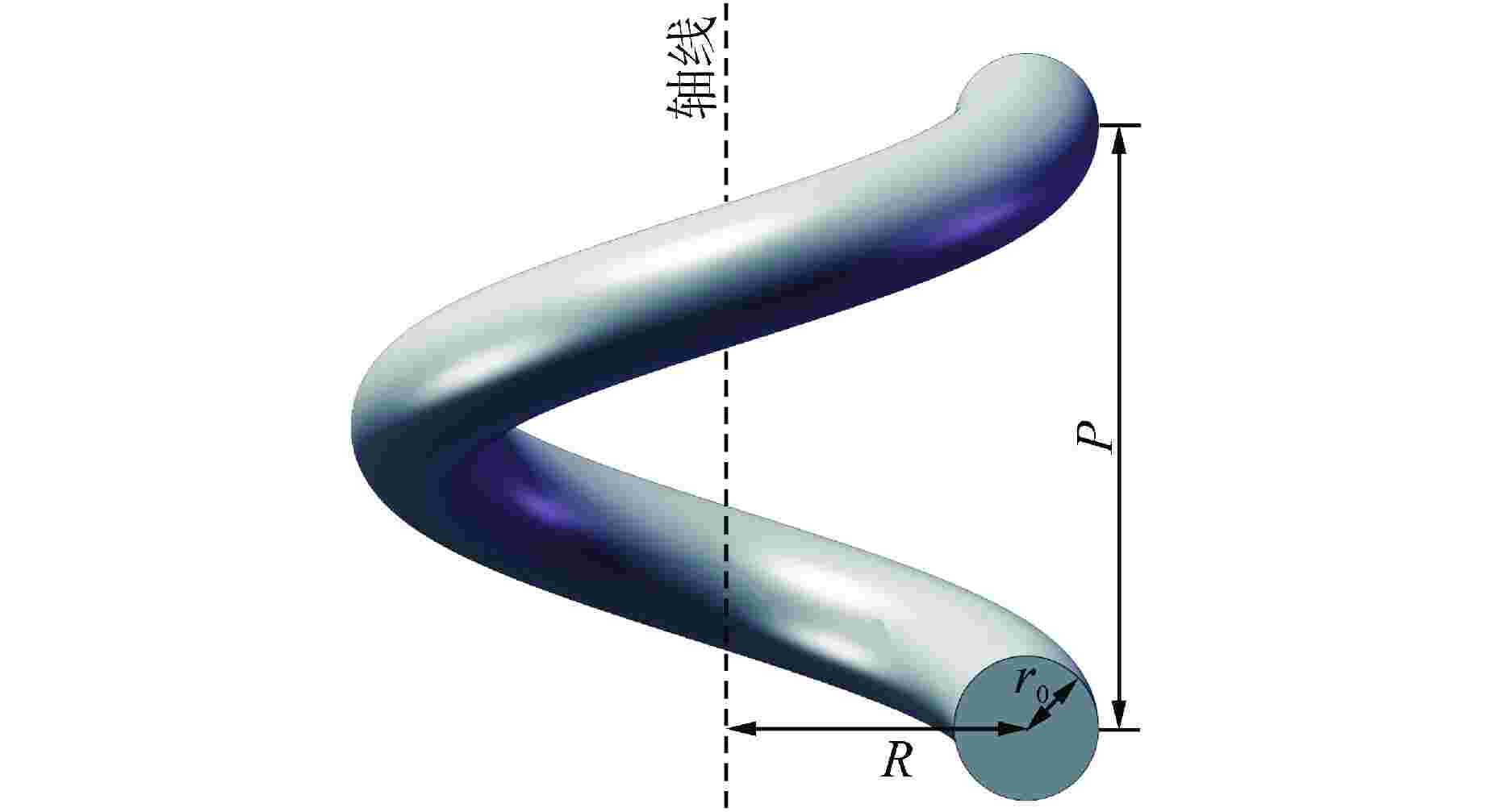
表 1 不同曲率螺旋管几何参数

Table 1. Geometric Parameters of Helical Tubes with Different Curvatures

δ	δ_mod	r₀/mm	R/mm	P/mm
0.02	0.0195	4	200	31
0.04	0.0390	4	100	16.5
0.06	0.0584	6	100	17
0.11	0.1038	4	36	16

下载: 导出CSV

表 2 不同网格间的最大相对误差

Table 2. Maximum Relative Error between Different Grids

δ	低精度网格数量/10⁵	高精度网格数量/10⁵	ζ_max/%
0.02	33.6	80.9	0.96
0.04	25.0	55.6	1.00
0.06	23.6	75.2	0.78

下载: 导出CSV

表 3 不同模型经验系数所计算的阻力系数

Table 3. Friction Factors with Different Model Coefficients

经验系数C_TU1	经验系数C_TU3	经验系数β^*	f
60	1	0.09	0.0334
70	1	0.09	0.0293
80	1	0.09	0.0248
90	1	0.09	0.0248
100	1.1	0.09	0.0248
100	1.2	0.09	0.0248
100	1.3	0.09	0.0248
100	1.4	0.09	0.0248
100	1	0.095	0.0247
100	1	0.098	0.0247
100	1	0.101	0.0247
100	1	0.104	0.0246

下载: 导出CSV

表 4 不同曲率下的C_TU1值

Table 4. C_TU1 for Different δ_mod

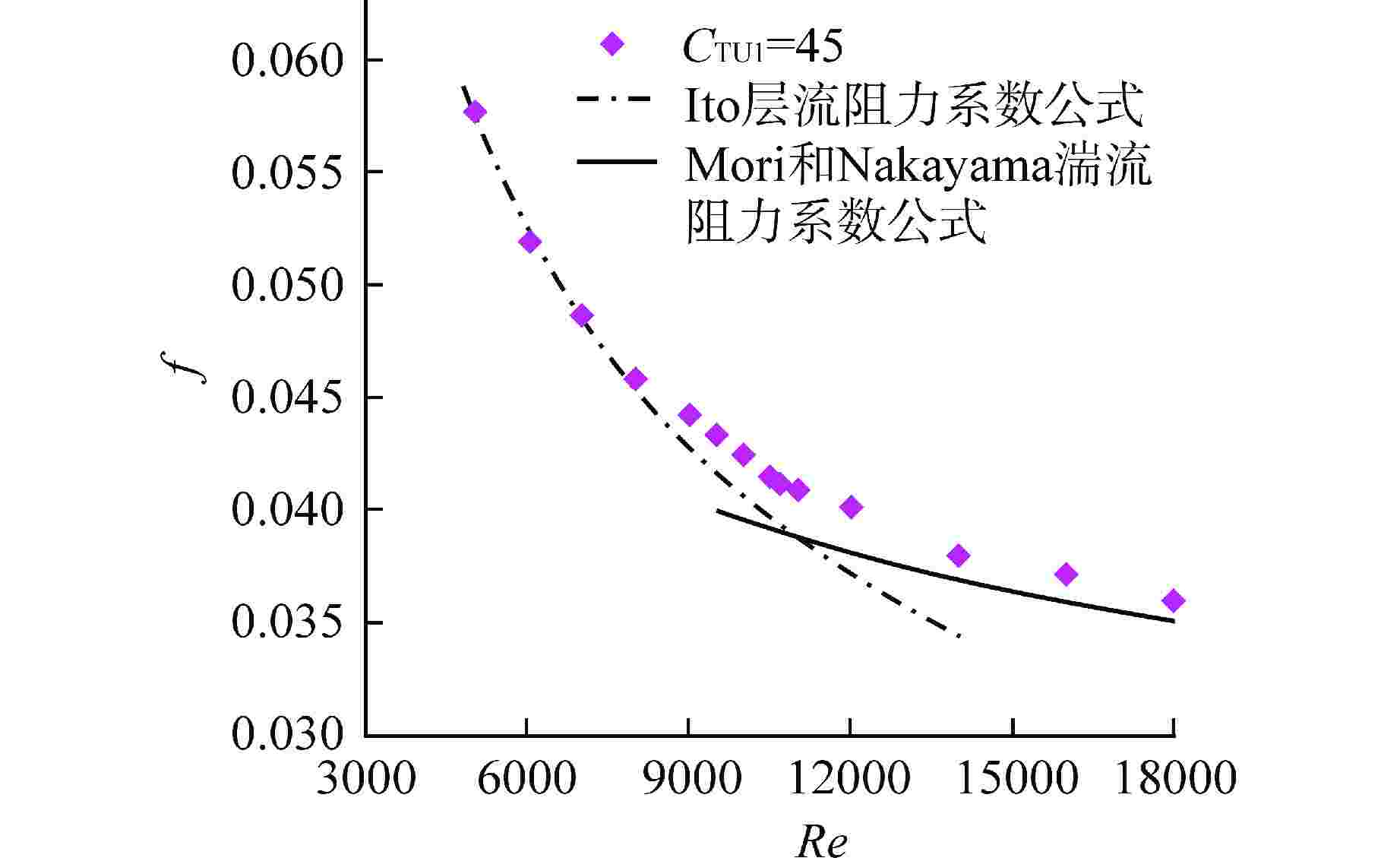
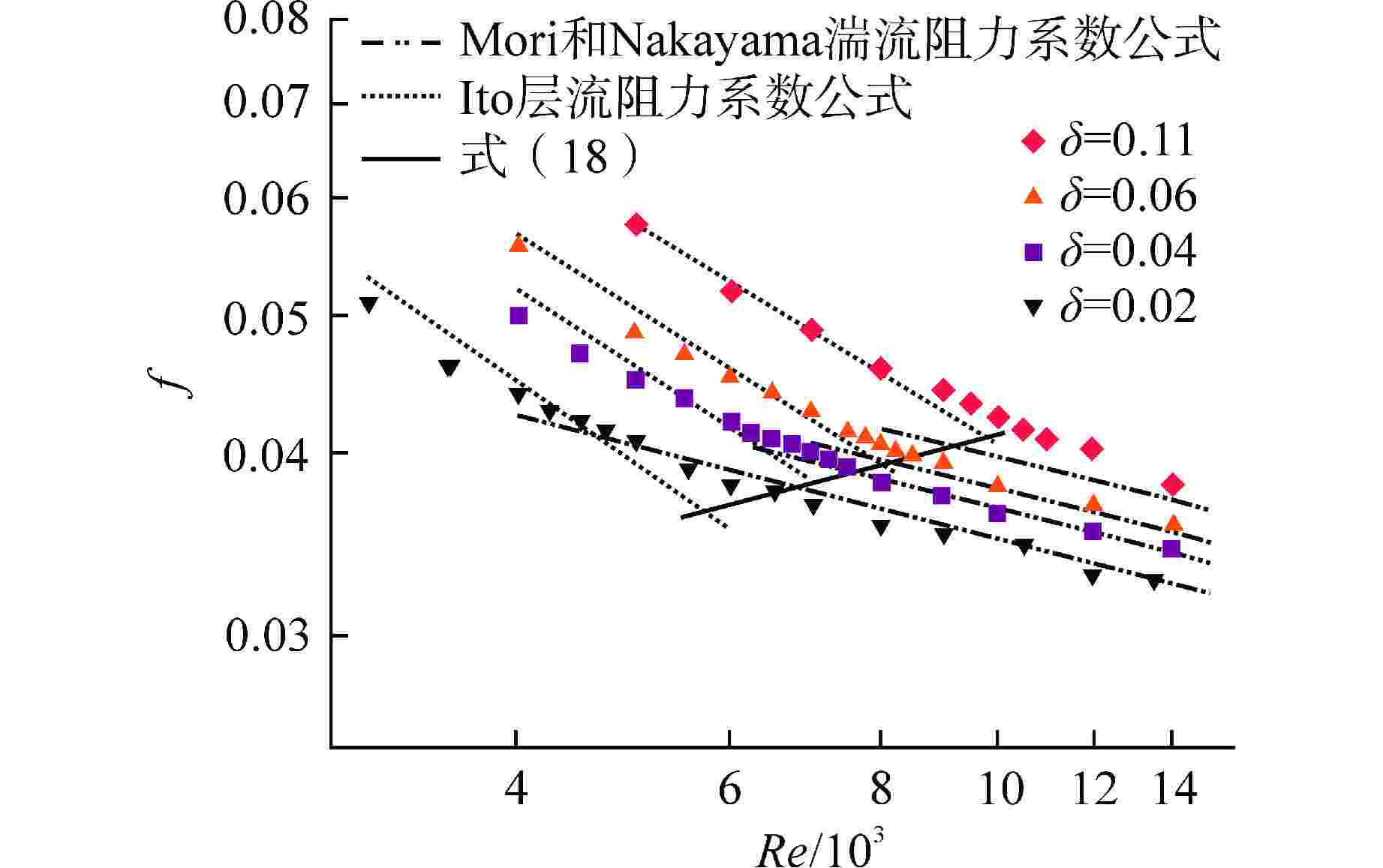
δ_mod	推荐C_TU1	Re_cri
δ_mod	推荐C_TU1	数值结果	式（18）
0.0195	50	5600	5700
0.0390	47	7300	7100
0.0584	46	8500	8100
0.1038	45	10700	9700

下载: 导出CSV

参考文献(16)

[1]	ZHAO H J, LI X W, WU X X. New friction factor equations developed for turbulent flows in rough helical tubes[J]. International Journal of Heat and Mass Transfer, 2016, 95: 525-534. doi: 10.1016/j.ijheatmasstransfer.2015.12.035
[2]	ZHAO H J, LI X W, WU X X. New friction factor and Nusselt number equations for turbulent convection of liquids with variable properties in circular tubes[J]. International Journal of Heat and Mass Transfer, 2018, 124: 454-462. doi: 10.1016/j.ijheatmasstransfer.2018.03.082
[3]	李晓伟,吴莘馨,张作义,等. 高温气冷堆示范工程螺旋管式直流蒸汽发生器工程验证试验[J]. 清华大学学报: 自然科学版,2021, 61(4): 329-337.
[4]	LI X W, GAO W K, SU Y, et al. Thermal analysis of HTGR helical tube once through steam generators using 1D and 2D methods[J]. Nuclear Engineering and Design, 2019, 355: 110352. doi: 10.1016/j.nucengdes.2019.110352
[5]	LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computational fluid dynamics codes[J]. AIAA Journal, 2009, 47(2): 2894-2906.
[6]	CONTENT C, HOUDEVILLE R. Application of the γ-R_θ laminar-turbulent transition model in Navier-Stokes computations[C]//40th Fluid Dynamics Conference and Exhibit. Chicago: AIAA, 2010.
[7]	MALAN P, SULUKSNA K, JUNTASARO E. Calibrating the γ-Re_θ transition model for commercial CFD[C]//47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2009.
[8]	GRABE C, KRUMBEIN A. Extension of the γ-Re_θt model for prediction of crossflow transition[C]//52nd Aerospace Sciences Meeting. National Harbor: AIAA, 2014.
[9]	MEDIDA S, BAEDER J. A new crossflow transition onset criterion for RANS turbulence models[C]//21st AIAA Computational Fluid Dynamics Conference. San Diego: AIAA, 2013.
[10]	DASSLER P, KOZULOVIC D, FIALA A. Transport equation for roughness effects on laminar-turbulent transition[C]//The 15th International Conference on Fluid Flow Technologies. Budapest, Hungary: CMFF, 2012.
[11]	MENTER F R, SMIRNOV P E, LIU T, et al. A one-equation local correlation-based transition model[J]. Flow, Turbulence and Combustion, 2015, 95(4): 583-619. doi: 10.1007/s10494-015-9622-4
[12]	ABRAHAM J P, SPARROW E M, GORMAN J M, et al. Application of an intermittency model for laminar, transitional, and turbulent internal flows[J]. Journal of Fluids Engineering, 2019, 141(7): 071204. doi: 10.1115/1.4042664
[13]	DI PIAZZA I, CIOFALO M. Transition to turbulence in toroidal pipes[J]. Journal of Fluid Mechanics, 2011, 687: 72-117. doi: 10.1017/jfm.2011.321
[14]	ZHAO H J, LI X W, WU Y J, et al. Friction factor and Nusselt number correlations for forced convection in helical tubes[J]. International Journal of Heat and Mass Transfer, 2020, 155: 119759. doi: 10.1016/j.ijheatmasstransfer.2020.119759
[15]	ITO H. Theoretical and experimental investigation concerning the flow through curved pipes[C]//Mem Inst High Speed Mech. Tohoku University, 1959.
[16]	MORI Y, NAKAYAMA W. Study of forced convective heat transfer in curved pipes (2nd report, turbulent region)[J]. International Journal of Heat and Mass Transfer, 1967, 10(1): 37-59.