Research on Optimization Control of Nuclear Power Plant Coordination System Based on ESO-MPC
-
摘要: 核岛与常规岛的调节特性具有较大差异,需要协调核岛与常规岛进行同步控制才能取得较好的控制效果,研究协调控制系统的优化控制策略具有重要意义。本文针对核电厂堆机协调控制系统容易出现扰动的现象,提出了一种基于扩张状态观测器(ESO)的模型预测控制(MPC)算法。所提出的方法通过使用ESO来精确估计外部干扰,然后将扰动估计值整合到MPC的滚动优化过程中,实现预测模型的自适应校正,从而得出所需的优化控制率。在仿真试验中,本文所提算法与比例积分微分控制和多变量模型预测控制器的效果进行了对比,结果显示,本文所提算法具有较好的表现效果。在机组负荷设定值扰动的场景中,本文所提算法的主蒸汽压力与机组负荷均方误差分别为0.06和0.02,明显优于其他两种算法。本文所提算法能够使得核电机组协调控制系统在存在外部干扰情况下实现精确的控制性能。
-
关键词:
- 核电机组 /
- 协调控制 /
- 模型预测控制(MPC) /
- 扩张状态观测器(ESO) /
- 扰动误差
Abstract: The regulation characteristics of nuclear island and conventional island are quite different, so it is necessary to coordinate the synchronous control of nuclear island and conventional island to achieve better control effect. It is of great significance to study the optimal control strategy of coordinated control system. In this paper, a model predictive control (MPC) algorithm based on extended state observer (ESO) is proposed to solve the problem that the coordinated control system of nuclear power plant is prone to disturbance. The proposed method accurately estimates the external disturbance by using ESO, and then integrates the disturbance estimation value into the rolling optimization process of MPC to realize the adaptive correction of the prediction model, thereby obtaining the required optimization control rate. In the simulation experiment, the algorithm proposed in this paper was compared with the performance of proportional integral differential control and multivariable model predictive controller, and the results showed that the algorithm proposed in this paper had good performance. In the scenario of unit load setting disturbance, the mean square error of main steam pressure and unit load by the proposed algorithm is 0.06 and 0.02 respectively, which is significantly better than the other two algorithms. The algorithm proposed in this paper can enable the coordinated control system of nuclear power units to achieve precise control performance in the presence of external disturbances. -
0. 引 言
我国将会积极安全有序地发展核电,到2025年,核电运行装机容量达到7000万千瓦左右,核电机组装机容量将会持续增加[1]。就目前全球核电的运行情况来看,除法国的部分核电机组实现了变负荷调峰运行之外,中美等国的核电机组还是以基本负荷模式运行为主。但是在高比例新能源电力系统需要灵活性时,核电机组改变以往以固定负荷为主的发电运行模式,参与电网的调峰调频,是未来的可能运行情景,并且目前设计的快堆以及海上小型堆已经要求具备较宽的负荷运行能力(20%FP~100%FP,FP表示满功率)[2-3]。压水堆核岛与常规岛的调节特性差异较大,需要研究和优化核电机组协调控制系统,从而实现将反应堆与汽轮机作为一个整体进行控制、满足多种运行方式与工况控制的目的。对协调控制系统进行研究和优化是进一步提升核电机组变负荷响应能力、维持机组运行安全的重要手段。
目前,压水堆核电机组实际运行上普遍以G模式运行为主[4],而G模式是以堆跟机为主的控制模式。在理论研究方面,核电厂协调控制系统目前研究的主流方向是基于现代控制理论的控制系统设计。席原等在参考其他行业的基础上,给出了核动力装置的协调控制系统架构,并论证了其可行性[5]。Eliasi等设计了一种用于负载跟随操作问题的鲁棒非线性模型预测控制器(NMPC),以确保氙振荡保持在可接受的范围内[6]。苏杰研究了汽轮机和直流蒸汽发生器的非线性模型预测控制方法,在工况变化时,所提方法能够较快地稳定核动力装置的输出[7]。张伟等在原有控制逻辑基础上引入了协调控制器,将冷却剂平均温度、出口蒸汽压力以及汽轮机转速作为控制量,与常规比例-积分-微分(PID)控制结构相比,有效提升了核电机组在变负荷下的控制效果[8]。成守宇等提出了专家系统和原控制器结合的协调控制器及其策略,并在全范围核动力装置模拟器上进行了仿真试验[9]。Zhao等提出了一体化压水堆系统的协调控制系统,包括控制策略和控制器设计,仿真结果证明该控制策略在协同控制及低负荷下均具有较高的稳定性[10]。钱虹等建立了核反应堆反应性和一回路平均温度之间的分段参数模型,并研究了多模型动态矩阵控制方法[11-12]。邓志光等提出了一种基于Attention 和 LSTM 组合模型(ALSTM)和广义预测控制(GPC)的协调控制系统优化控制器[13]。李雅君研究了单堆双机核动力装置的运行过程,建立了相应的数学动态模型,设计了基于多变量模型预测控制的协调控制系统[14]。王岱鹏辨识了多个工况下的堆机协调控制模型,然后设计了多变量动态矩阵控制(DMC)控制方案[15]。Dong等提出了一种基于无源性的高温气冷堆功率压力协调控制方法,给出了全局渐近闭环稳定的充分条件,并在仿真模型上进行了验证,其效果优于传统PID控制结构[16]。Cui等基于机理方程给出了面向控制器设计的堆机协调简化模型,并设计了多变量模型预测控制器[17]。Wang等提出了针对小型压水堆的协调控制方案,并在甩负荷场景中进行了验证[18]。核电机组协调控制系统的优化设计方案是当前的研究热点,模型预测控制(MPC)是堆机协调控制中的重要方向。
MPC在工业控制领域获得了广泛的应用,通常包括预测模型、滚动优化与反馈校正等环节,主要有DMC、模型算法控制(MAC)、GPC等几种控制算法[19]。对于可以利用动力学方程较为准确描述动态特性的动力系统来说,可以直接利用控制对象的模型信息,推导出相应的MPC来实现精确控制。然而,实际模型往往存在着模型参数或运行工况偏差导致的扰动,模型方程难以准确描述实时状态时,需要寻找一种合适的观测器来获取扰动信息[20]。扩张状态观测器(ESO)自提出之时便得到了持续的关注。ESO可以同时实现对被观测对象的状态变量及所受扰动的观测功能,且对模型准确性的要求不高,因此在火电、核电、机械等多个工业控制过程中得到了广泛的应用[21-23]。
压水堆核电机组协调控制系统在运行中容易面临氙振荡、给水流量波动、冷却剂流量波动等未知扰动,本文通过使用ESO来精确估计外部干扰,然后分析ESO的估计误差与预测误差之间的关系,进而将扰动估计值整合到MPC的滚动优化过程中,实现预测模型的自适应校正,从而得出所需的优化控制率。本文所提ESO-MPC算法可以在存在外部干扰和约束(包括输入和状态约束)的情况下提升压水堆核电机组协调控制系统的精确控制。
1. 核电机组协调控制模型
1.1 压水堆核电机组运行结构
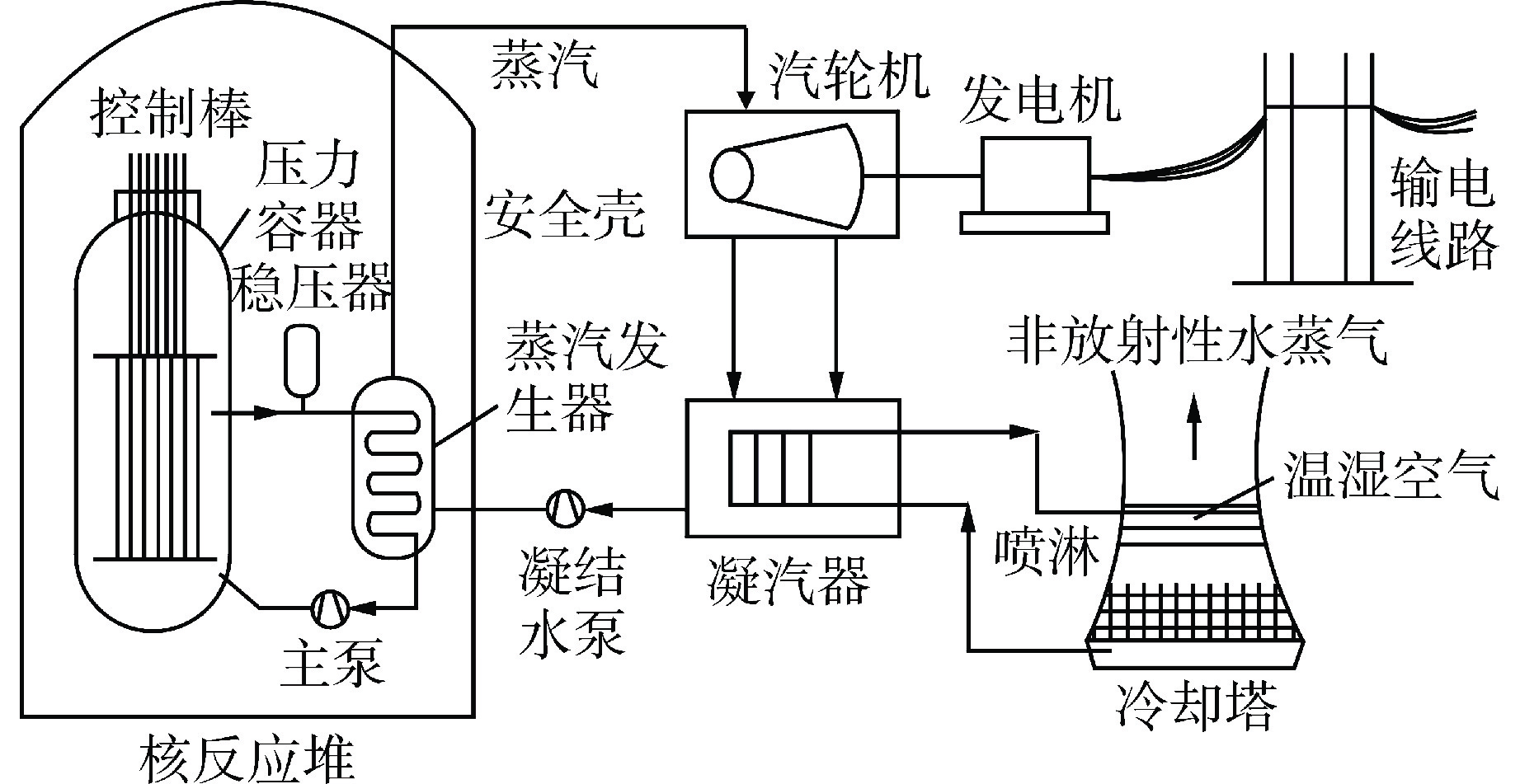
现有压水堆核电机组的运行结构如图1所示,主要由核反应堆、汽轮机、发电机、凝汽器、冷却塔等部分组成。在核反应堆中,堆芯核燃料与中子作用产生核裂变反应,释放出能量,能量的释放可以通过移动控制棒棒位来调节。释放出的能量由冷却剂吸收并带出,在蒸汽发生器中完成热量的传递,热量将传递给二回路的汽水工质,汽水工质在汽轮机中完成做功,产生电能,从而完成能量的转化。
在压水堆核电厂中,控制棒棒位直接控制一回路温度,与给水控制相结合,对主蒸汽压力和蒸汽发生器水位进行控制,汽轮机进汽流量由主蒸汽阀门开度进行控制。由于核反应堆存在着时间迟滞性,而汽轮机响应较快,因此,总体来说,主蒸汽压力与汽轮机负荷组成协调被控对象。被控对象的输入为汽轮机阀门开度(ut)和控制棒位移(uz),被控对象的输出则为主蒸汽压力(ps)和汽轮机功率(Ne)。
1.2 压水堆核电机组协调控制模型
本文所用模型来自于文献[13],该文献在某900 MW 压水堆核电厂模型基础上,开展阶跃仿真试验,利用仿真数据和最小二乘法辨识得到压水堆核电厂协调控制系统的动态传递函数矩阵模型。
核电机组的协调控制模型为:
$$ \left[ {\begin{array}{*{20}{c}} {{p_{\text{s}}}} \\ {{N_{\text{e}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{G_{11}}(s)}&{{G_{12}}(s)} \\ {{G_{21}}(s)}&{{G_{22}}(s)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_{\text{z}}}} \\ {{u_{\text{t}}}} \end{array}} \right] $$ (1) $$ {G_{11}}(s) = \frac{{0.00036}}{{1 + 18s}}{{\text{e}}^{ - 5s}} $$ $$ {G_{12}}(s) = \frac{{ - 0.0435}}{{1 + 5s}} $$ $$ {G_{21}}(s) = \frac{{0.292}}{{(1 + 18s)(1 + 12s)}}{{\text{e}}^{ - 5s}} $$ $$ {G_{22}}(s) = \frac{{42s}}{{(1 + 5s)(1 + 12s)}} $$ 式中,$ s $为复数变量,代表拉普拉斯变换中的变量;G11(s)、G12(s)、G21(s)、G22(s)均为传递函数,由仿真数据拟合得到。
观察该模型具有以下特征:控制棒位移对于主蒸汽压力、机组负荷的作用存在一定的迟延,而阀门开度对主蒸汽压力和机组负荷的影响则相对较快;阀门开度对主蒸汽压力变化呈负相关性;阀门开度对主蒸汽压力的响应较快,而对机组负荷的作用存在一定的惯性。以上特征符合对核电机组运行特性的一般认知。
2. 基于扰动观测器的MPC
2.1 控制系统结构
考虑扰动的压水堆核电机组协调控制系统标称模型为:
$$ x(k + 1) = {\boldsymbol{A}}x(k) + {\boldsymbol{B}}u(k) + d(k) $$ (2) 式中,x(k)为第k个时刻的系统状态;$ {\boldsymbol{A}} $、$ {\boldsymbol{B}} $为线性化后系统模型[式(1)]的参数矩阵;u(k)为系统输入;d(k)为系统未知不确定扰动,其中系统状态可测。
与传统的控制框架不同,MPC在每个采样时刻用当前测量信息更新优化问题,为控制系统提供最优执行指令。MPC的控制率的计算可转化为在线求解二次规划问题得到:
$$ J[x(k),u(k)] = \sum\limits_{i = 0}^N {[\parallel x(k + i|k){\parallel _{\boldsymbol{Q}}}} + \left.\|u(k+i \mid k)\|_{{\boldsymbol{R}}}\right] $$ (3) $$ \mathrm{s}.\mathrm{t}.\ \ x(k+1)=\boldsymbol{A}x(k)+\boldsymbol{B}x(k)+d(k) $$ 式中,$ J $为目标函数;$ N $为预测时域长度;$ i $表示第$ i $个控制时域;$ {\boldsymbol{Q}} $、$ {\boldsymbol{R}} $为正定权重矩阵,$ x(k|k) = x(k) $。
假设d(k)在预测时域内保持不变,可以得到式(4):
$$ x(k + 1|k) = {\boldsymbol{A}}x(k|k) + {\boldsymbol{B}}u(k) + d(k) $$ $$ \begin{gathered} x(k + 2|k) = {{\boldsymbol{A}}^2}x(k|k) + {\boldsymbol{AB}}u(k) + {\text{ }}{\boldsymbol{B}}u(k + 1) + ({\boldsymbol{A}} + {\boldsymbol{I}})d(k) \end{gathered} $$ $$ \begin{gathered} x(k + 3|k) = {{\boldsymbol{A}}^3}x(k|k) + {{\boldsymbol{A}}^2}{\boldsymbol{B}}u(k) + {\boldsymbol{AB}}u(k + 1) + \\ \qquad {\boldsymbol{A}}u(k + 2) + ({{\boldsymbol{A}}^2}{\boldsymbol{ + A + I}})d(k) \\ \vdots \end{gathered} $$ $$ \begin{split} x(k + N|k) = & {{\boldsymbol{A}}^N}x(k|k) + {{\boldsymbol{A}}^{N - 1}}{\boldsymbol{B}}u(k) + \\ & {{\boldsymbol{A}}^{N - 2}}{\boldsymbol{B}}u(k + 1) + \ldots + {\boldsymbol{A}}u(k + N - 1) + \\ & ({{\boldsymbol{A}}^{N - 1}} + {{\boldsymbol{A}}^{N - 2}} + \ldots + {\boldsymbol{I}})d(k) \end{split} $$ (4) 式中,$ I $为单位矩阵。
定义:
$$ \begin{split} {\boldsymbol{X}}(k + 1|k) = & [x(k + 1|k),x(k + 2|k),\\ & x(k + 3|k), \cdots ,x(k + N|k){]^{\text{T}}} \end{split} $$ (5) $$ {\boldsymbol{U}}(k) = [u(k),u(k + 1), u(k + 2), \cdots ,u(k + N - 1){]^{\text{T}}} $$ (6) 式中,$ {\boldsymbol{U}}(k) $表示$ k $时刻的控制量。
式(4)可进一步推导得到:
$$ {\boldsymbol{X}}(k + 1|k) = {{\boldsymbol{H}}_{\text{x}}}x(k) + {{\boldsymbol{H}}_{\text{u}}}{\boldsymbol{U}}(k) + {{\boldsymbol{H}}_{\text{d}}}d(k) $$ (7) $$ {{\boldsymbol{H}}_{\text{x}}} = {[{\boldsymbol{A}},{{\boldsymbol{A}}^2},{{\boldsymbol{A}}^3}, \cdots ,{{\boldsymbol{A}}^N}]^{\mathrm{T}}} $$ $$ \begin{split} {{\boldsymbol{H}}_{\text{u}}} =& [{\boldsymbol{B}},{\boldsymbol{AB}} + {\boldsymbol{B}},{{\boldsymbol{A}}^2}{\boldsymbol{B}} + {\boldsymbol{AB}} + {\boldsymbol{B}},\cdots ,{{\boldsymbol{A}}^{N - 1}}{\boldsymbol{B}} + \\ & {{\boldsymbol{A}}^{N - 2}}{\boldsymbol{B}} + \cdots + {\boldsymbol{AB}} + {\boldsymbol{B}}{]^{\text{T}}} \end{split} $$ $$ \begin{split} {{\boldsymbol{H}}_{\text{d}}} = & [{\boldsymbol{I}},{\boldsymbol{A}} + {\boldsymbol{I}},{{\boldsymbol{A}}^2} + {\boldsymbol{A}} + {\boldsymbol{I}},\cdots ,{{\boldsymbol{A}}^{N - 1}} + \\ & {{\boldsymbol{A}}^{N - 2}} + \cdots + {\boldsymbol{A}} + {\boldsymbol{I}}{]^{\text{T}}} \end{split} $$ 式中,$ {{\boldsymbol{H}}_{\text{x}}} $、$ {{\boldsymbol{H}}_{\text{u}}} $、$ {{\boldsymbol{H}}_{\text{d}}} $均表示与系统状态矩阵等相关的控制器参数矩阵。
将式(7)带入式(3)可求解得:
$$ {\boldsymbol{U}}(k) = ({\boldsymbol{H}}_{\text{u}}^{\text{T}}{{\boldsymbol{R}}^{\text{T}}}{\boldsymbol{R}}{{\boldsymbol{H}}_{\text{u}}} + {{\boldsymbol{Q}}^{\text{T}}}{\boldsymbol{Q}}{)^{ - 1}}{\boldsymbol{H}}_{\text{u}}^{\text{T}}{{\boldsymbol{R}}^{\text{T}}}{\boldsymbol{R}}{{\boldsymbol{E}}_{\text{p}}}(k + 1|k) $$ (8) 式中,$ {{\boldsymbol{E}}_{\text{p}}}(k + 1|k) = - {{\boldsymbol{H}}_{\text{x}}}x(k|k) - {{\boldsymbol{H}}_{{\text{nd}}}}d(k) $,$ {{\boldsymbol{H}}_{{\text{nd}}}} $为扰动项的最优补偿系数矩阵。
由于MPC只应用第一个时刻控制率,即:
$$ u(k)=[1,0,\cdots ,0] \cdot {\boldsymbol{U}}(k) \text={{\boldsymbol{K}}}_{\text{mpc}} \cdot {{\boldsymbol{E}}}_{\text{p}}(k+1|k) $$ (9) $$ {{\boldsymbol{K}}}_{\text{mpc}}=[1,0,\cdots ,0] \cdot ({{\boldsymbol{H}}}_{\text{u}}^{\text{T}}{{\boldsymbol{R}}}^{\text{T}}{\boldsymbol{R}}{{\boldsymbol{H}}}_{\text{u}} {{\boldsymbol{Q}}^{\text{T}}}{\boldsymbol{Q}}{)^{ - 1}}{\boldsymbol{H}}_{\text{u}}^{\text{T}}{{\boldsymbol{R}}^{\text{T}}}{\boldsymbol{R}} $$ (10) 式中,$ {{\boldsymbol{K}}_{{\text{mpc}}}} $表示与系统状态矩阵等相关的控制器参数矩阵。
则控制率可推导为:
$$ u(k) = - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}x(k|k) - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}}d(k) $$ (11) 则系统的闭环方程可推导为:
$$ {x^*}(k + 1) = {\boldsymbol{A}}{x^*}(k) + {\boldsymbol{B}}[ - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}{x^*}(k) - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}}d(k)] + d(k) $$ (12) $${x^*}(k + 1) = ({\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}){x^*}(k) - ({\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}} - {\boldsymbol{I}})d(k) $$ (13) 式中,$ {x^*} $为理想轨迹的系统状态量。
2.2 引入ESO
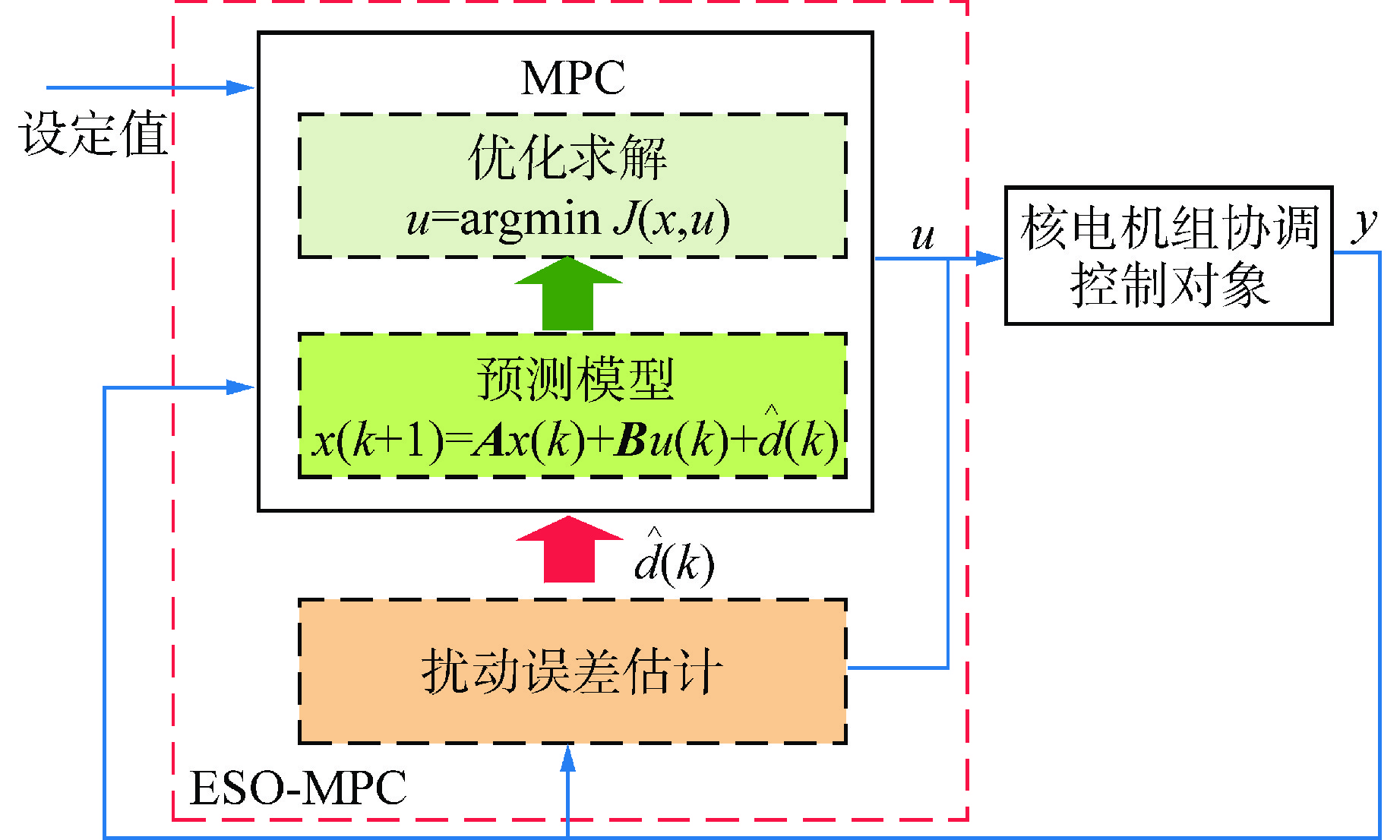
由于实际系统中的扰动往往都是未知的,不可量测的,此时MPC策略中滚动优化过程将无法保证性能的实时最优性。如要实现扰动下的系统的最优控制,可通过设计扰动观测器将系统不确定项估计出来,实现模型的在线更新,降低模型不确定性。如图2所示,首先通过扰动误差估计获得不确定扰动量$\hat d(k)$,然后将其带入MPC的预测模型中,进行MPC的滚动优化求解,从而获得理想的控制量。
设计ESO为:
$$ \begin{split} \hat x(k + 1) = & {\boldsymbol{A}}\hat x(k) + {\boldsymbol{B}}u(k) + \hat d(k) + \\ & {\beta _1}[x(k) - \hat x(k)] \end{split} $$ $$ \hat d(k + 1) = - {\beta _2}[x(k) - \hat x(k)] $$ (14) 式中,$ \hat x $为ESO估计的系统状态量;$\hat d$为不确定扰动估计值;β1和β2为ESO设计参数。
则耦合扰动观测器后的模型预测控制系统方程可描述为:
$$ \left[ {\begin{array}{*{20}{c}} {x(k + 1)} \\ {\hat x(k + 1)} \\ {\hat d(k + 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{A}}&0&{\boldsymbol{I}} \\ {{\beta _1}}&{{\boldsymbol{A}} - {\beta _1}}&1 \\ { - {\beta _2}}&{ - {\beta _2}}&1 \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {x(k)} \\ {\hat x(k)} \\ {\hat d(k)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\boldsymbol{B}} \\ {\boldsymbol{B}} \\ 0 \end{array}} \right]u(k) $$ (15) $$ u(k) = - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}x(k|k) - {{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}}\hat d(k) $$ 闭环系统方程表示为:
$$\begin{split}& \left[ {\begin{array}{*{20}{c}} {x(k + 1)} \\ {\hat x(k + 1)} \\ {\hat d(k + 1)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}}&0&{{\boldsymbol{I}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{d}}}} \\ {{\boldsymbol{A}} + {\beta _1} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}}&{ - {\beta _1}}&{{\boldsymbol{I}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{d}}}} \\ { - {\beta _2}}&{ - {\beta _2}}&0 \end{array}} \right] \cdot \\ & \qquad\qquad\qquad\qquad\quad \left[ {\begin{array}{*{20}{c}} {x(k)} \\ {\hat x(k)} \\ {\hat d(k)} \end{array}} \right] \\[-67pt] \end{split}$$ (16) 将系统的理想轨迹与实际轨迹作差:
$$ \begin{split} & {x^*}(k + 1) - x(k + 1){\text{ = }}({\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}}){x^*}(k) + \\ &\qquad ({\boldsymbol{I}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}})d(k) - ({\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}})x(k) - \\ &\qquad ({\boldsymbol{I}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}})\hat d(k) \end{split} $$ (17) 令$ e(k + 1) = {x^*}(k + 1) - x(k + 1) $,则:
$$ e(k + 1) = ({\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}})e(k) + ({\boldsymbol{I}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{{\text{nd}}}})[d(k) - \hat d(k)] $$ (18) 式中,$ e(k) $代表$ k $时刻的误差。由于$ {\boldsymbol{A}} - {\boldsymbol{B}}{{\boldsymbol{K}}_{{\text{mpc}}}}{{\boldsymbol{H}}_{\text{x}}} $是赫尔维兹矩阵,且扰动估计误差有界,则误差$ e(k) $系统关于原点渐进稳定,即$ \mathop {\lim }\limits_{k \to \infty } e(k) \to 0 $。
3. 仿真与结果分析
3.1 单一工况下的控制效果分析
为对所提算法的有效性进行验证,在式(1)所示模型上开展仿真验证。仿真采样时间为0.1 s,对比组为PID控制器以及MPC,ESO-MPC为本文所提算法。设置以下3个工况进行仿真试验:
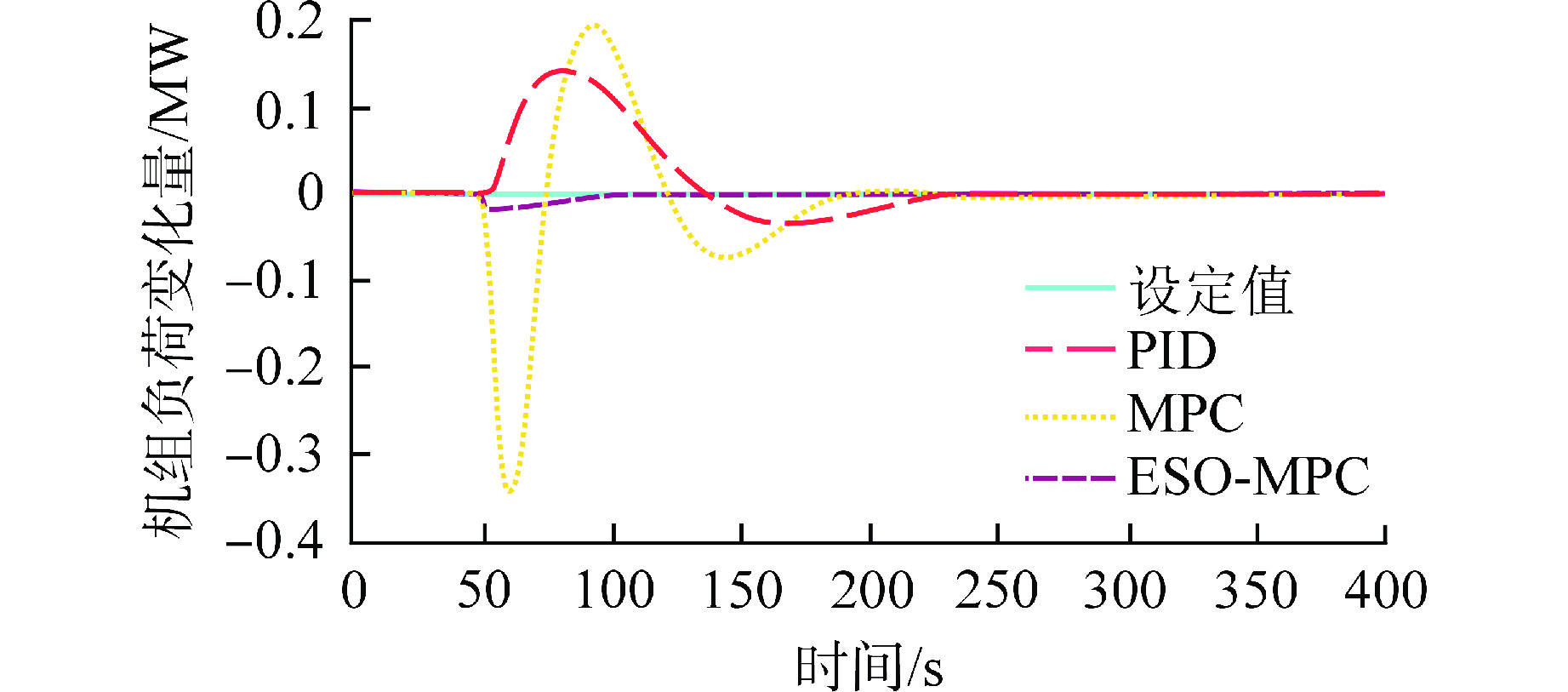
工况1:在50 s处对机组负荷设定值添加一个斜坡信号,设定值信号限速为0.5 MW/s,幅度为5 MW,主蒸汽压力设定值不变。
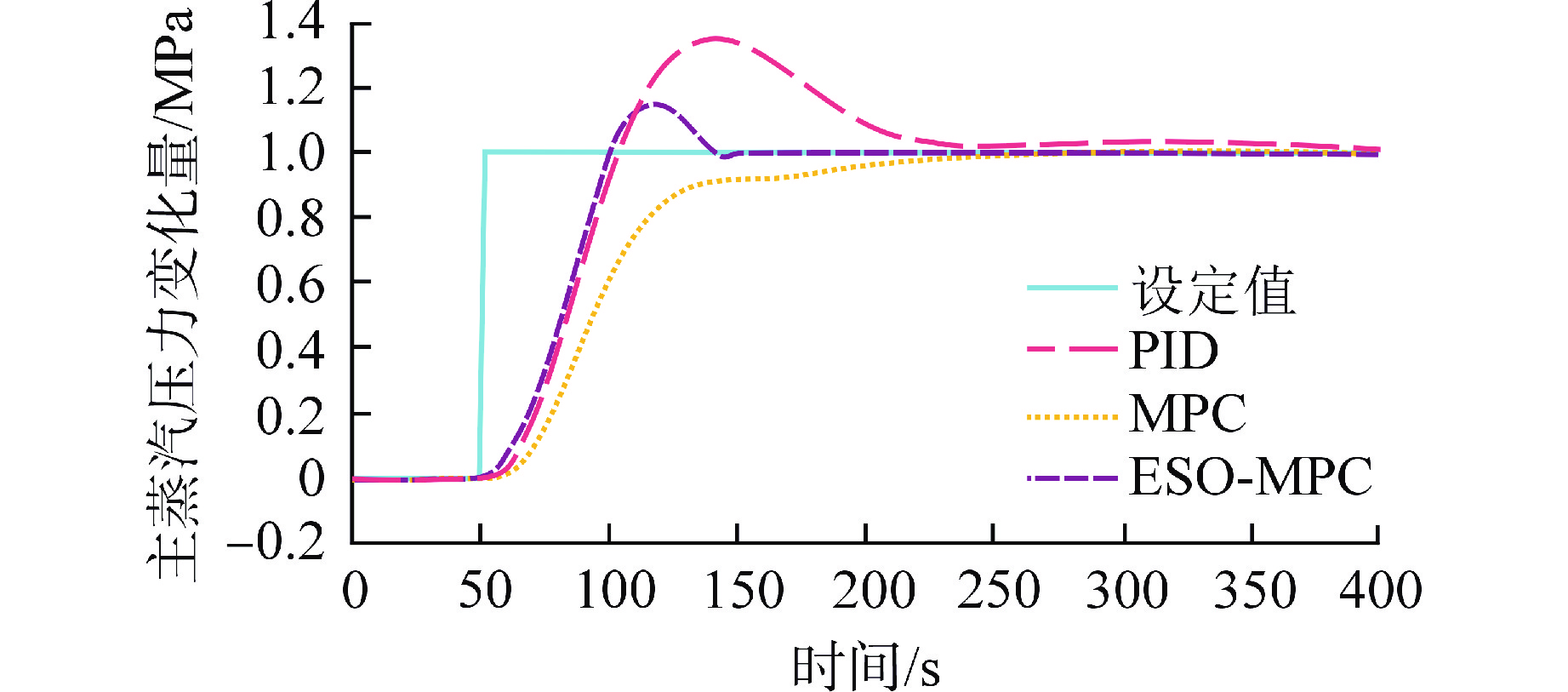
工况2:在50 s处对主蒸汽压力设定值添加一个斜坡信号,设定值信号限速为0.5 MPa/s,幅度为1 MPa,机组负荷设定值不变。
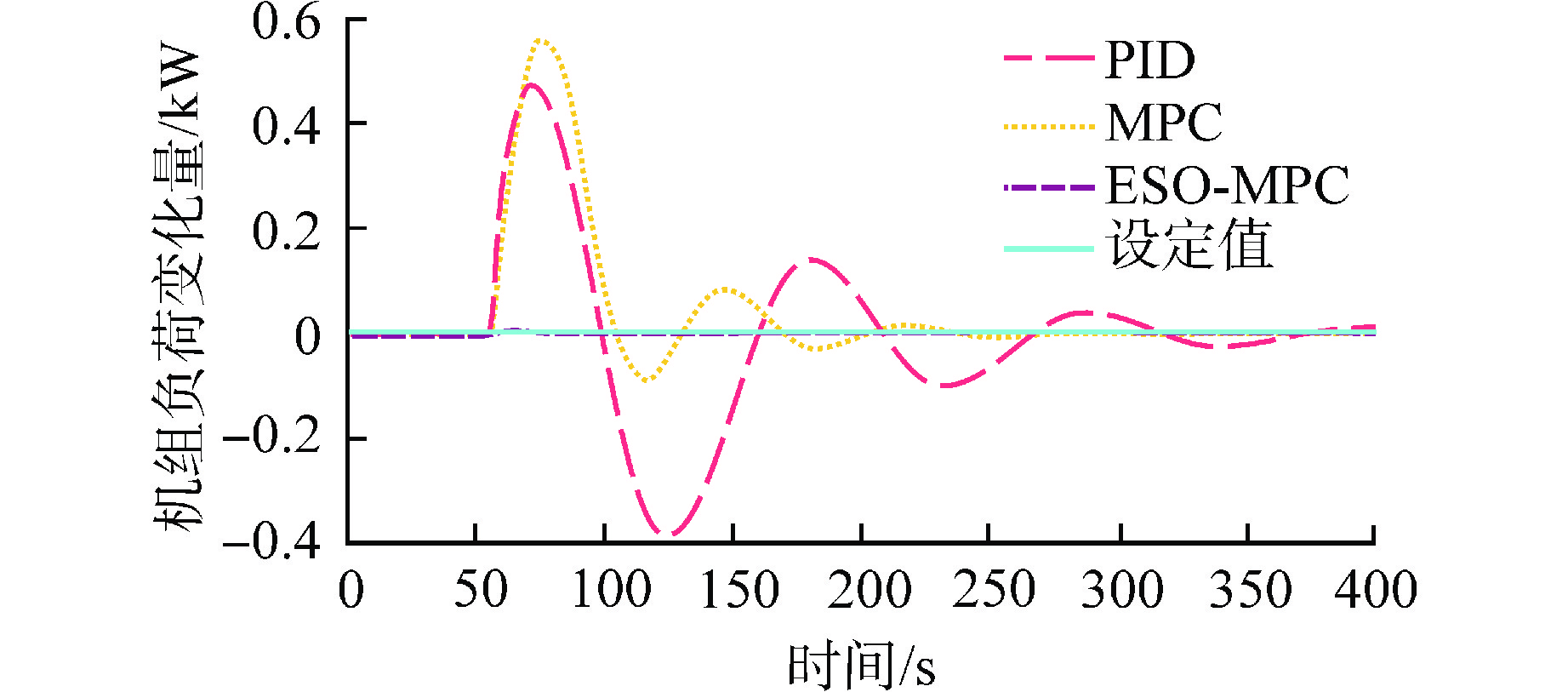
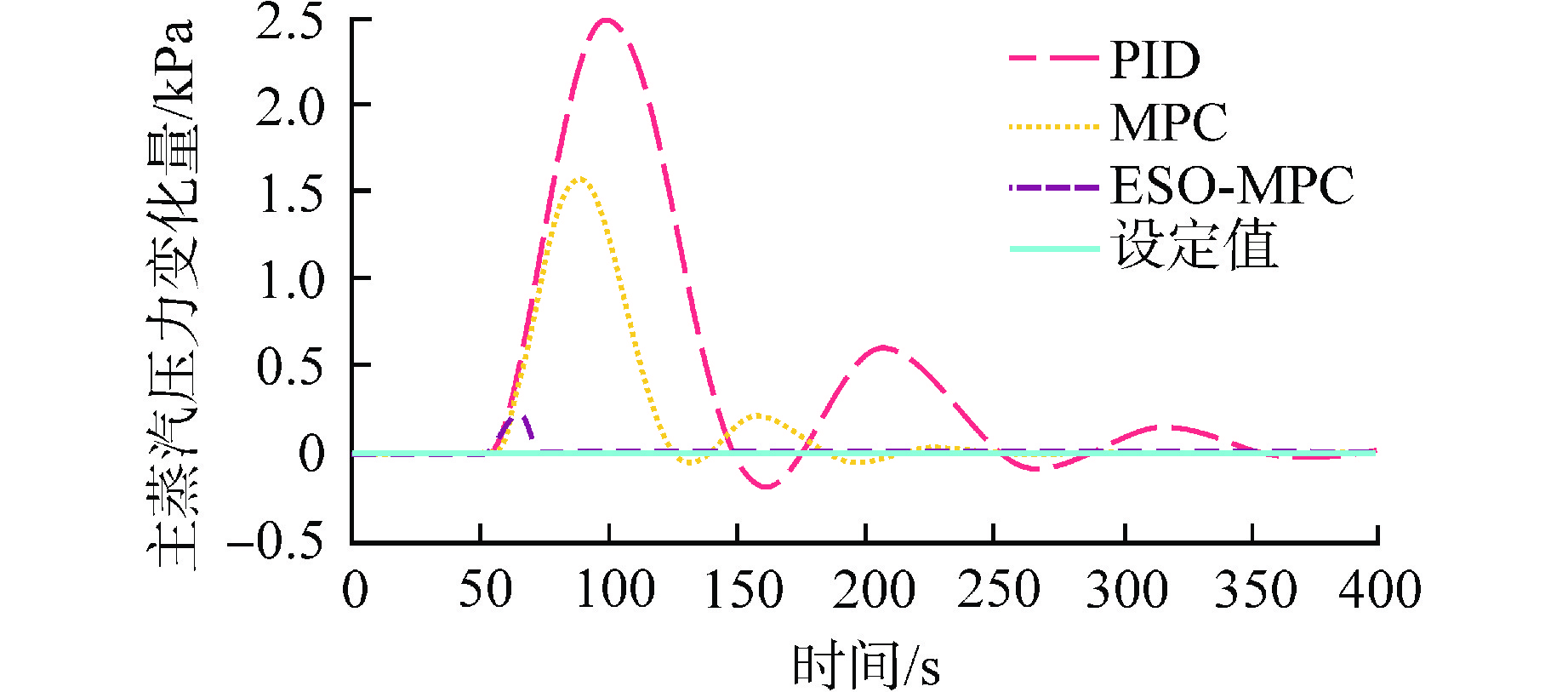
工况3:在50 s处给控制棒棒位添加一个10 cm的扰动。机组负荷与主蒸汽压力的设定值均保持为0。
控制效果的评价采用与设定值的均方误差(MSE),MSE的计算方法如下所示:
$$ {\mathrm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({y_i} - {{\tilde y}_i})}^2}} $$ (19) 式中,n为数据段的长度;yi为模型输出;$ {\tilde y_i} $为设定值。
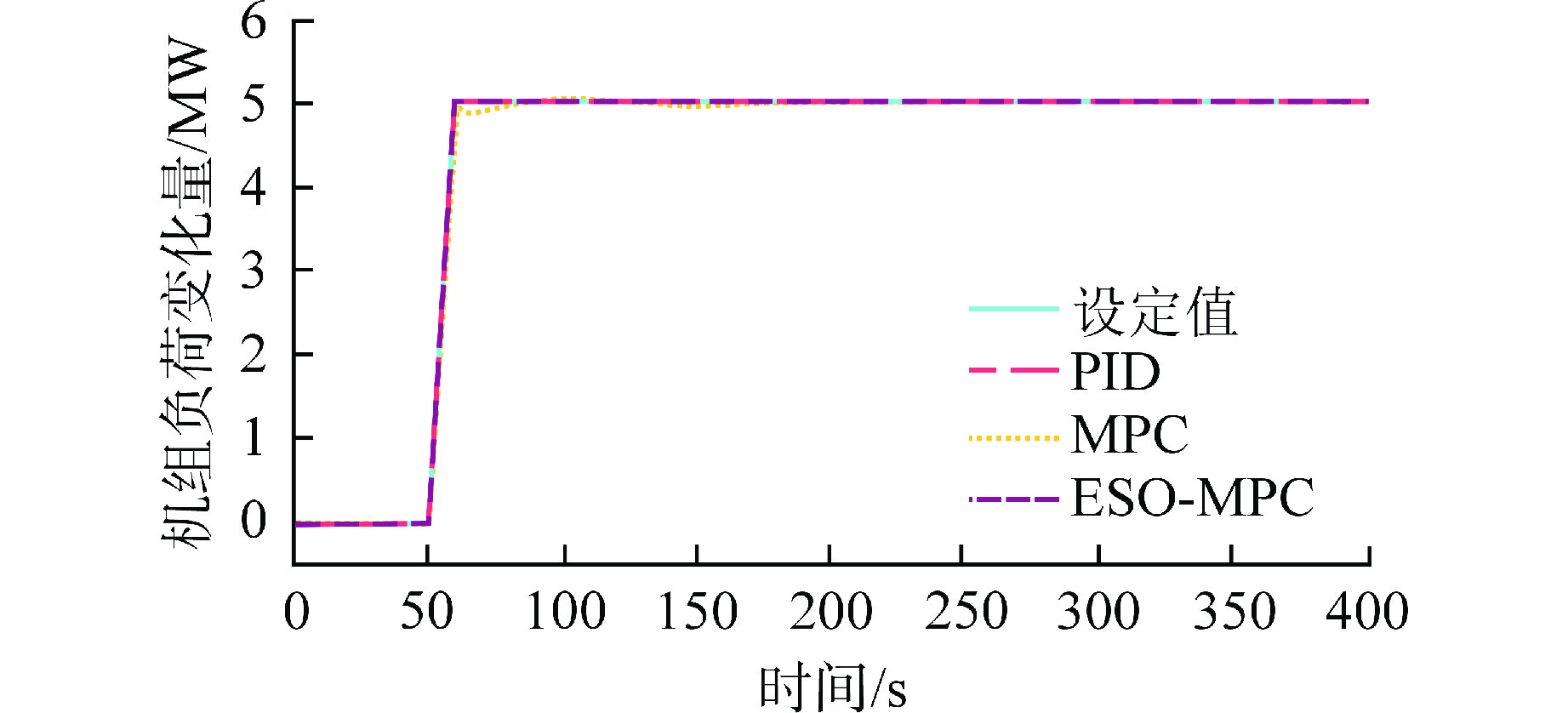
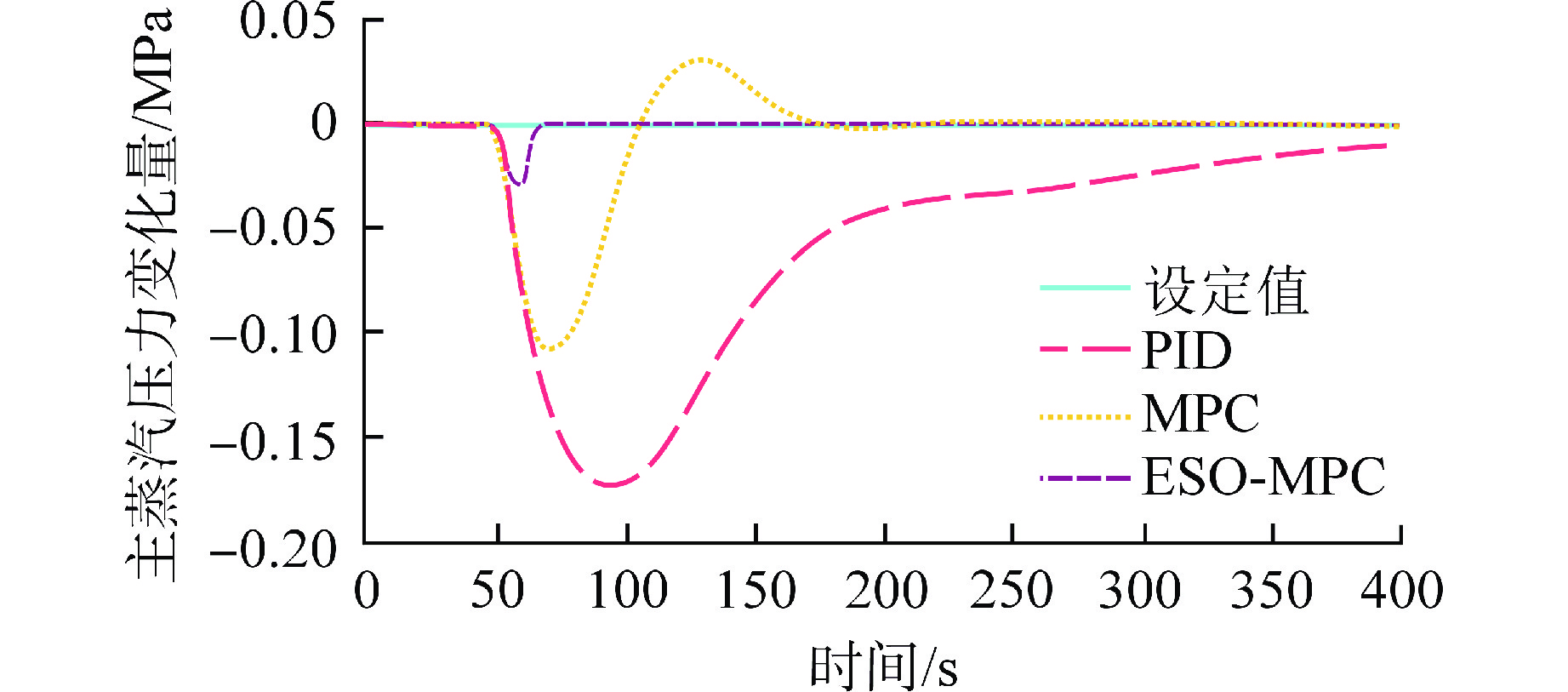
工况1的仿真结果如图3和图4所示,工况2的仿真结果如图5和6所示,工况3的仿真结果如图7和8所示。所有仿真结果的数值评价结果如表1所示。
表 1 控制效果分析Table 1. Control Effect Analysis算法 工况 1 工况 2 工况 3 MSE(Ne) MSE(ps) MSE(Ne) MSE(ps) MSE(Ne) MSE(ps) PID 0.52 21.05 8.61 310.16 1.1×10−4 2.5×10−3 MPC 1.24 3.35 26.55 305.58 7.5×10−5 6.8×10−4 ESO-MPC 0.02 0.06 0.07 277.40 1.5×10−8 5.1×10−6 在工况1中,机组负荷设定值添加了5 MW的一个扰动信号,但是由于汽轮机阀门响应相对较快,汽轮机阀门的快速动作使得机组负荷能够快速响应设定值要求,在不同控制算法中均能达到满意的效果,如图3所示。因此工况1中的机组负荷MSE都相对较小。然而由于棒位的控制相对滞后,主蒸汽压力不可避免地出现较大的偏差,如图4所示。但是本文所提的算法能够较快地使棒位动作,尽快克服扰动,从而使主蒸汽压力最快返回设定值。从主蒸汽压力的MSE结果上看,PID控制器的偏差最大,达到了21.05,MPC能改善效果,达到了3.35,而本文所提算法的结果仅为0.06。以上试验说明了本文所提算法在克服机组负荷扰动时的有效性。
在工况2中,机组的主蒸汽压力设定值添加了1 MPa的扰动信号,接收到主蒸汽压力设定值变化时,控制棒棒位开始变化,同时由于主蒸汽压力的上升,同步引起机组负荷的变化。如图5所示,本文所提算法在抑制扰动上具有明显的效果,能够较快地调节返回至0功率数值处,机组负荷的MSE为0.07,与其他两种算法的比较中具有明显的优势。如图6所示,本文算法同样能较快地使主蒸汽压力跟踪设定值,MSE达到228.43,具有明显优势。
在工况3中,在50 s时对控制棒棒位添加了10 cm的扰动,可以看到扰动添加后机组主蒸汽压力与机组负荷均出现了扰动,以上控制算法均能抑制扰动,使被控量返回至设定值。但是,ESO-MPC的控制效果最佳,产生的偏差最小,扰动消除的时间最短,MSE最小,说明ESO-MPC对内部扰动具有良好的抑制能力。
4. 结 论
针对核电机组堆机协调控制问题,本文提出了一种基于ESO的MPC方法。所提出的方法通过使用ESO来精确估计外部干扰,同时本文还分析了观测器的估计误差与预测误差之间的关系,然后将扰动估计值整合到MPC的滚动优化过程中,实现预测模型的自适应校正,从而得出所需的优化控制率。这种设计理念使本文所提方法有别于现有的扰动估计补偿方法。除此之外,递归可行性和输入到状态的稳定性得到了严格的证明,放松了紧缩约束和终端约束的条件,保证了控制器的稳定性和最优性。
为对所提算法的有效性进行验证,本文基于压水堆核电机组协调控制模型开展了仿真试验。结果显示,在主蒸汽压力、机组负荷设定值扰动以及控制棒、阀门开度的扰动试验中,本文所提方法具有更快的响应速度、更小的被控量波动。其中在机组负荷设定值扰动中,本文所提方法在主蒸汽压力的MSE结果为0.06,明显优于PID控制器的21.05以及多变量模型预测控制器的3.35。
然而本文所提算法依然依赖于内部更新模型的准确性,内部更新模型若误差较大将严重影响控制效果。核电机组是一个典型的非线性系统,在宽负荷运行时,核电机组的调节特性具有明显的差异性。因此,下一步将研究与验证ESO-MPC在核电机组多工况模型下的适应性。
-
表 1 控制效果分析
Table 1. Control Effect Analysis
算法 工况 1 工况 2 工况 3 MSE(Ne) MSE(ps) MSE(Ne) MSE(ps) MSE(Ne) MSE(ps) PID 0.52 21.05 8.61 310.16 1.1×10−4 2.5×10−3 MPC 1.24 3.35 26.55 305.58 7.5×10−5 6.8×10−4 ESO-MPC 0.02 0.06 0.07 277.40 1.5×10−8 5.1×10−6 -
[1] 杜祥琬,叶奇蓁,徐銤,等. 核能技术方向研究及发展路线图[J]. 中国工程科学,2018, 20(3): 17-24. [2] 郑洁,余凡,朱军民,等. 海洋核动力装备国内外发展现况与前景展望[J]. 中国工程科学,2023, 25(3): 62-73. [3] 陈智,廖龙涛,张英,等. ACP100S浮动核电站核蒸汽供应系统控制系统分析与仿真研究[J]. 南华大学学报(自然科学版),2018, 32(6): 9-14. [4] 刘同先,李庆,王晨琳,等. Mode-C运行与控制模式设计技术研究[J]. 原子能科学技术,2021, 55(1): 121-127. doi: 10.7538/yzk.2020.youxian.0085 [5] 席原,刘景宾. 单元机组协调控制系统研究进展[J]. 工业仪表与自动化装置,2011(5): 10-16,101. doi: 10.3969/j.issn.1000-0682.2011.05.003 [6] ELIASI H, MENHAJ M B, DAVILU H. Robust nonlinear model predictive control for nuclear power plants in load following operations with bounded xenon oscillations[J]. Nuclear Engineering and Design, 2011, 241(2): 533-543. doi: 10.1016/j.nucengdes.2010.12.004 [7] 苏杰. 核动力装置非线性模型预测协调控制仿真研究[J]. 核科学与工程,2011, 31(2): 104-110. [8] 张伟,丁宗华,夏国清,等. 协调控制技术在核动力系统中的应用研究[J]. 核科学与工程,2006, 26(4): 337-342. doi: 10.3321/j.issn:0258-0918.2006.04.010 [9] 成守宇,彭敏俊,刘新凯,等. 基于数字化仪控技术的核动力装置协调控制器的设计[J]. 原子能科学技术,2014, 48(S1): 576-581. [10] ZHAO Y X, DU X, XIA G L, et al. A novel coordinated control for integrated pressurized water reactor[J]. Annals of Nuclear Energy, 2015, 85: 1029-1034. doi: 10.1016/j.anucene.2015.07.022 [11] 钱虹,金蔚霄. 基于多模型动态矩阵预测的冷却剂平均温度控制[J]. 热力发电,2015, 44(11): 98-103,108. doi: 10.3969/j.issn.1002-3364.2015.11.098 [12] 钱虹,房振鲁,金蔚霄,等. 核电厂反应堆冷却剂平均温度预测控制及仿真研究[J]. 核动力工程,2016, 37(2): 91-96. [13] 邓志光,青先国,吴茜,等. ALSTM-GPC在核电厂协调控制系统中的应用[J]. 核动力工程,2021, 42(S2): 41-47. [14] 李雅君. 单堆双机核动力装置建模与控制方法研究[D]. 南京: 东南大学,2020. [15] 王岱鹏. 动态矩阵控制在核动力系统堆机协调中的应用研究[D]. 保定: 华北电力大学,2022. [16] DONG Z, LI B W, HUANG X J, et al. Power-pressure coordinated control of modular high temperature gas-cooled reactors[J]. Energy, 2022, 252: 124042. doi: 10.1016/j.energy.2022.124042 [17] CUI C C, ZHANG J L, SHEN J. System-level modeling, analysis and coordinated control design for the pressurized water reactor nuclear power system[J]. Energy, 2023, 283: 128472. doi: 10.1016/j.energy.2023.128472 [18] WANG L N, CHEN C Q, CHEN L K, et al. A coordinated control methodology for small pressurized water reactor with steam dump control system[J]. Energy, 2023, 282: 129008. doi: 10.1016/j.energy.2023.129008 [19] CASTELLETTI A, FICCHÌ A, COMINOLA A, et al. Model predictive control of water resources systems: a review and research agenda[J]. Annual Reviews in Control, 2023, 55: 442-465. doi: 10.1016/j.arcontrol.2023.03.013 [20] LI P, TONG X S, JIN W T, et al. Observer based model predictive current control of distorted grid connected single phase rectifier without AC voltage sensor[J]. Control Engineering Practice, 2023, 138: 105589. doi: 10.1016/j.conengprac.2023.105589 [21] 杨志军,高忠义,王丽君,等. 面向刚柔耦合定位平台的模型预测控制算法[J]. 吉林大学学报(工学版),2022, 52(12): 2806-2815. [22] CHEN C, PAN L, SUN L, et al. Generalized ESO based stable predictive tracking control for micro gas turbine cogeneration system[J]. Journal of the Franklin Institute, 2022, 359(11): 5148-5173. doi: 10.1016/j.jfranklin.2022.05.051 [23] HUI J W, LEE Y K, YUAN J Q. ESO-based adaptive event-triggered load following control design for a pressurized water reactor with samarium–promethium dynamics[J]. Energy, 2023, 271: 127058. doi: 10.1016/j.energy.2023.127058 -







 下载:
下载:








 下载:
下载: