A Preliminary Study on Aerosol Transport Characteristics in Containment Based on DPM Method
-
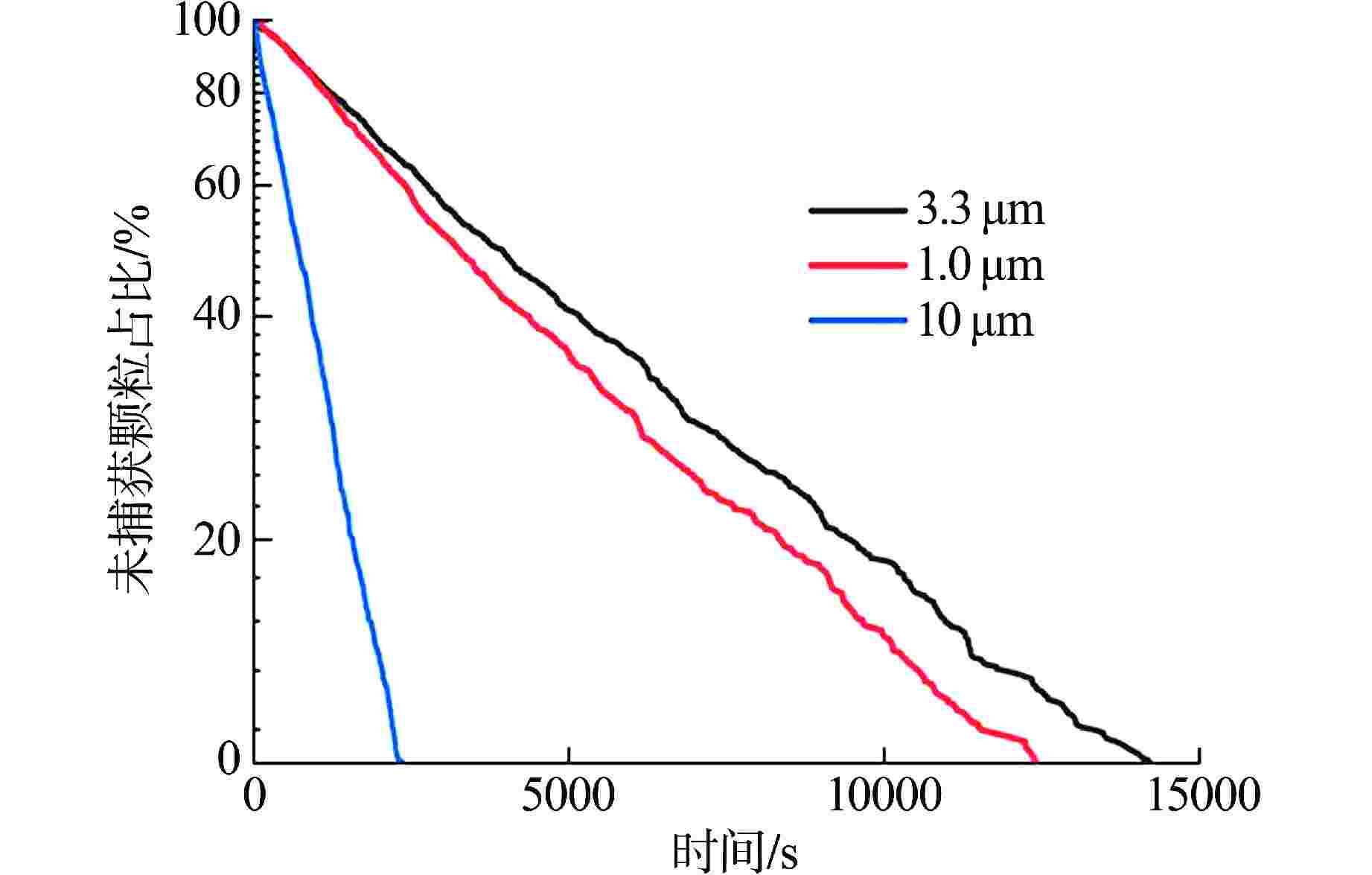
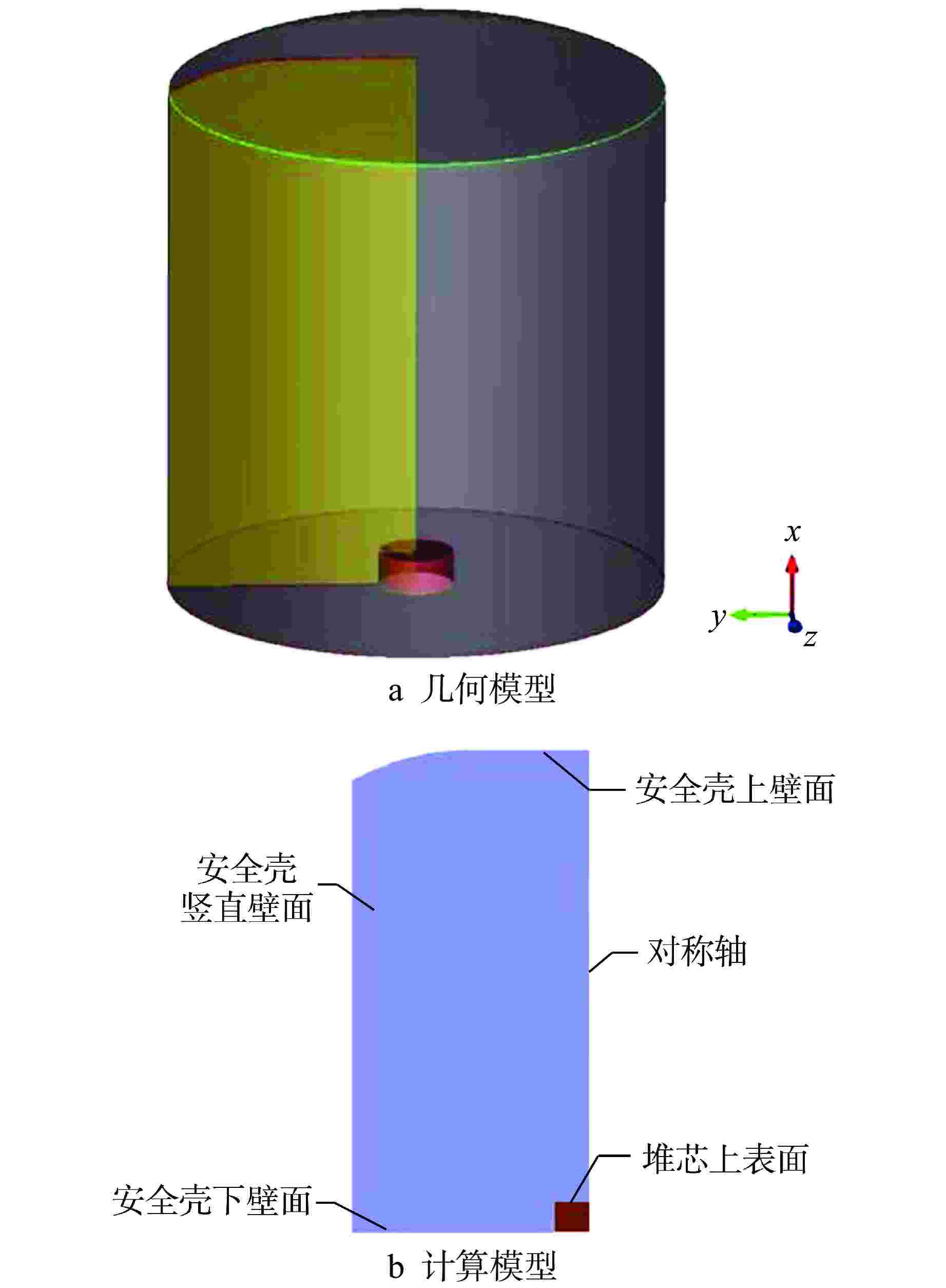
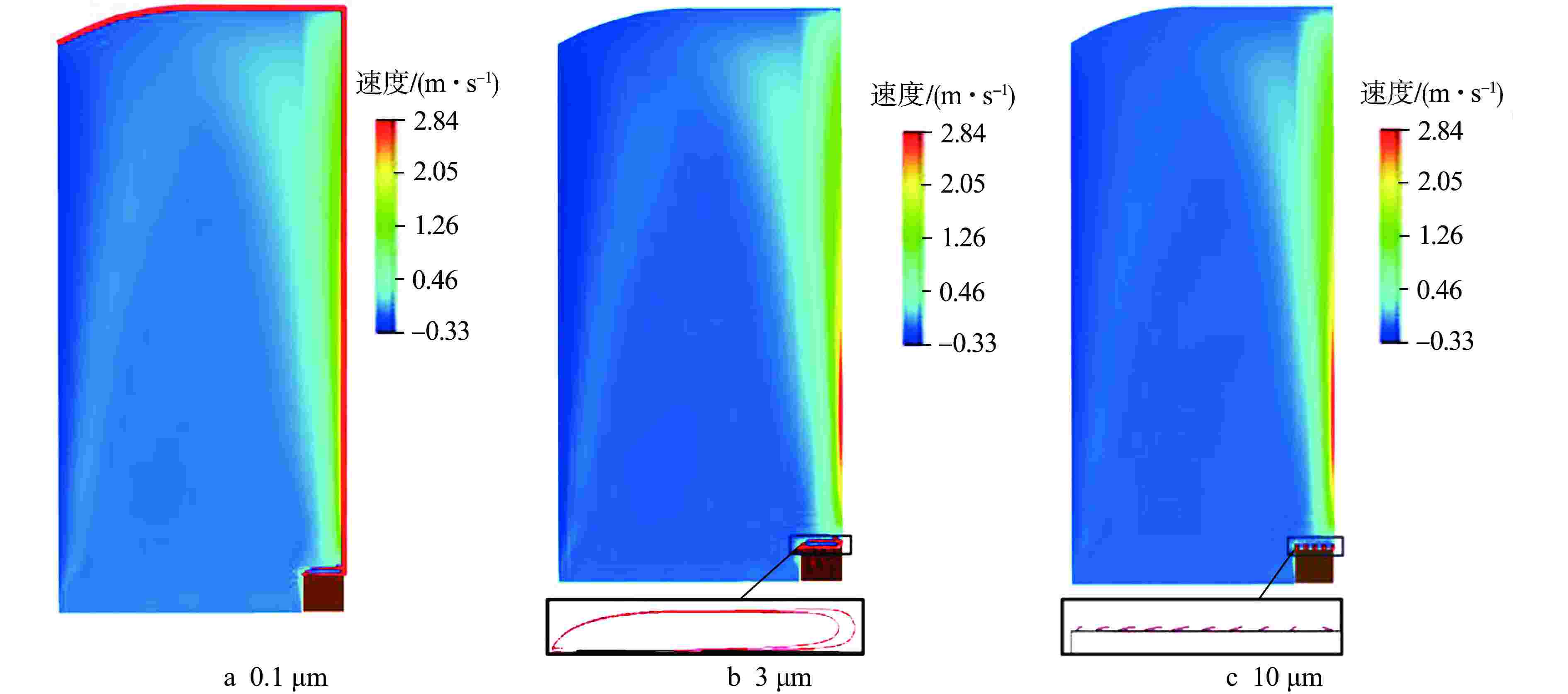
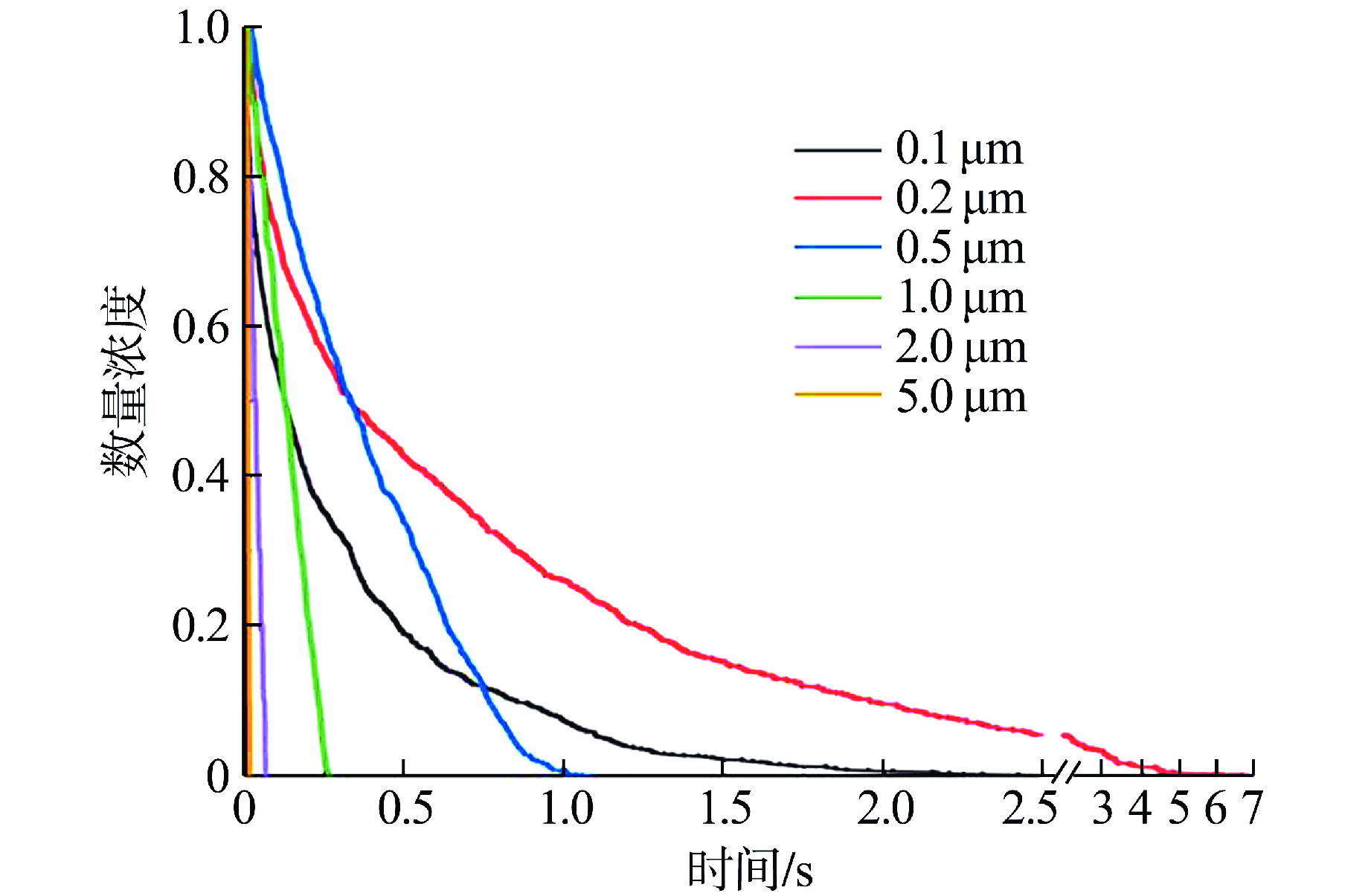
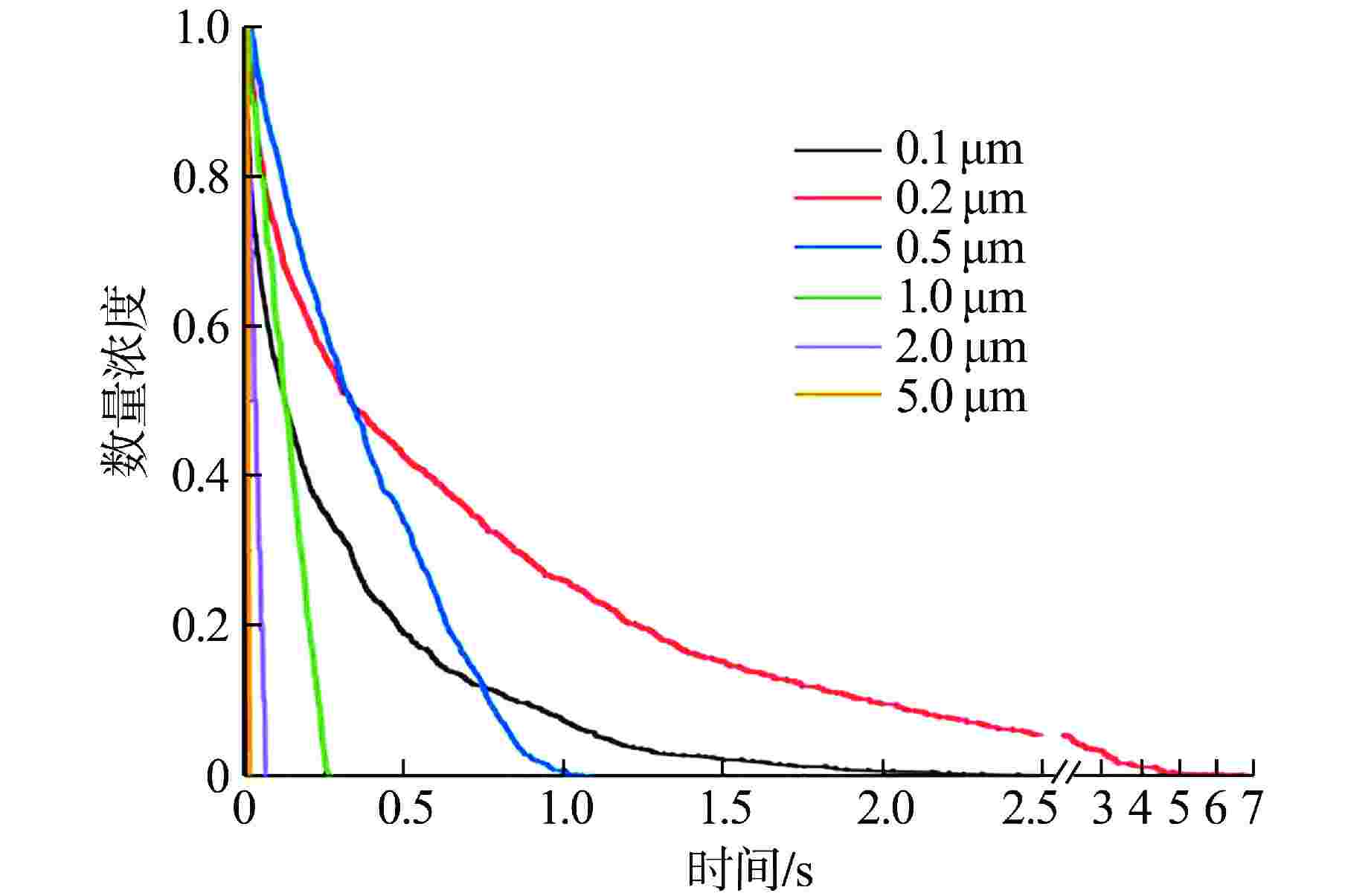
摘要: 核电厂在正常运行和发生严重事故时，气溶胶是放射性物质的主要泄漏途径。本文基于流体仿真软件FLUENT中欧拉-拉格朗日方法的离散相模型（DPM），针对铅基堆安全壳内气溶胶输运特性开展数值模拟研究。模拟结果显示静止流场中气溶胶小粒径颗粒受布朗力的驱动在不同壁面的沉降数量分布较均匀；大粒径颗粒受重力的驱动在不同壁面的沉降数量分布不均匀。同时，以PHEBUS FP T0实验的沉降阶段作为基准工况，验证了模型方法在安全壳环境下的适用性与准确性。最后，基于安全壳的二维轴对称简化模型，模拟了反应堆正常运行工况下从堆芯表面到安全壳中的气溶胶迁移和沉降过程。研究发现，在正常运行工况下，粒径0.1 μm的气溶胶会随流线进行大范围的迁移并在安全壳上壁面和竖直壁面的交界附近被捕获，粒径3 μm和10 μm的气溶胶会滞留在安全壳下壁面附近或沉降到安全壳下壁面。基于本模型研究得到的初步结论，可为后续开展的气溶胶受力分析实验和安全壳内气溶胶迁移实验提供参考。
-
关键词:
- 气溶胶 /
- 离散相模型（DPM） /
- 安全壳 /
- 压水堆 /
- 铅基堆
Abstract: Aerosols are the main leakage pathway of radioactive materials in nuclear power plants during normal operation and severe accidents. In this thesis, a numerical simulation study is carried out based on the Discrete Phase Model (DPM) of the Euler-Lagrange method in FLUENT for the aerosol transport characteristics in the containment of a lead-based reactor. The simulation results show that the number of aerosol small-size particles in the static flow field is uniformly distributed by Brownian force on different walls, and the number of large-size particles is unevenly distributed by gravity on different walls. Meanwhile, the applicability and accuracy of the modeling approach in the containment environment are verified by using the settling phase of the PHEBUS FPT0 experiment as a benchmark condition. Finally, based on a two-dimensional axisymmetric simplified model of a typical containment, the aerosol migration and settling processes from the core surface to the containment are simulated under the normal operating conditions of the reactor. It is found that under normal operating conditions, 0.1 μm aerosols will migrate widely with the flow line and be captured near the junction of the upper and vertical containment walls, while 3 μm and 10 μm aerosols will be retained near the lower containment wall or settle to the lower containment wall. The preliminary conclusions based on this modeling study can provide reference for the subsequent aerosol force analysis experiments and aerosol migration experiments in containment.-
Key words:
- Aerosol /
- Discrete phase model (DPM) /
- Containment /
- Pressurized water reactor /
- Lead-based reactor
-
图 1 不同粒径气溶胶颗粒的数量衰减曲线
Figure 1. Number Attenuation Curves of Aerosol Particles with Different Particle Sizes
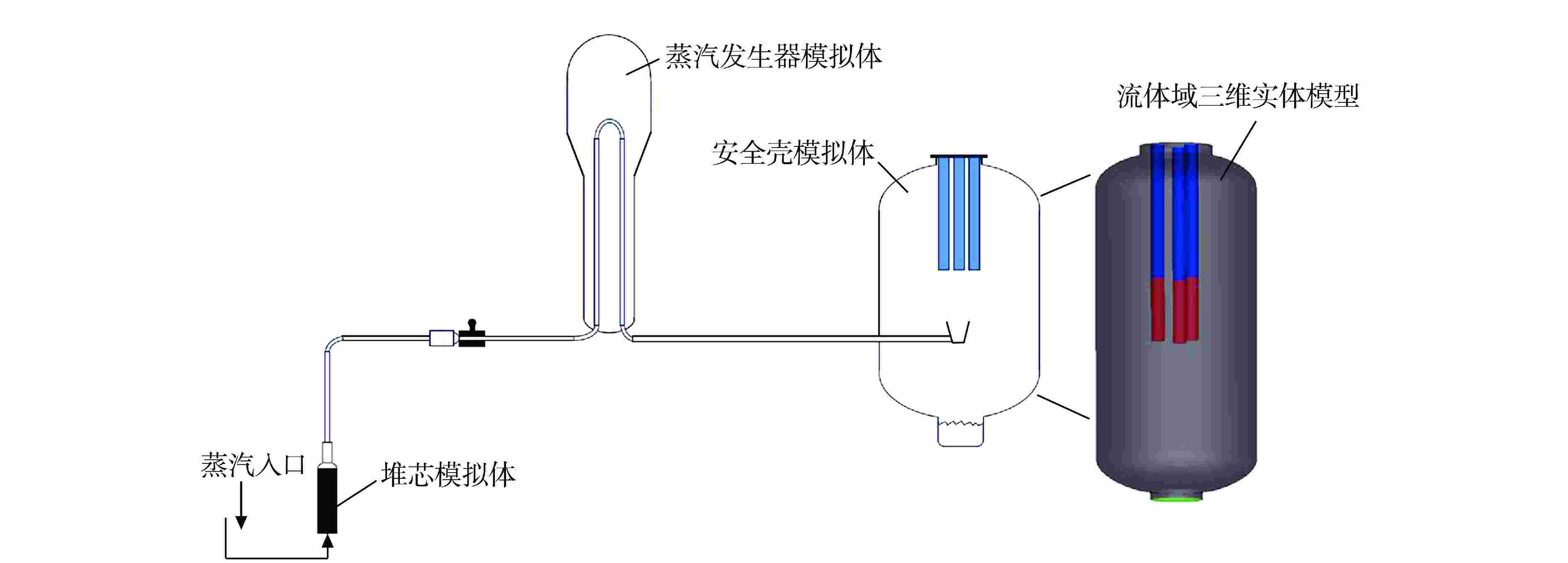
图 2 PHEBUS FP实验装置简化图[11]以及流体域三维实体模型
Figure 2. Simplified Diagram of PHEBUS FP Experimental Device and Fluid Field 3D Computational Model
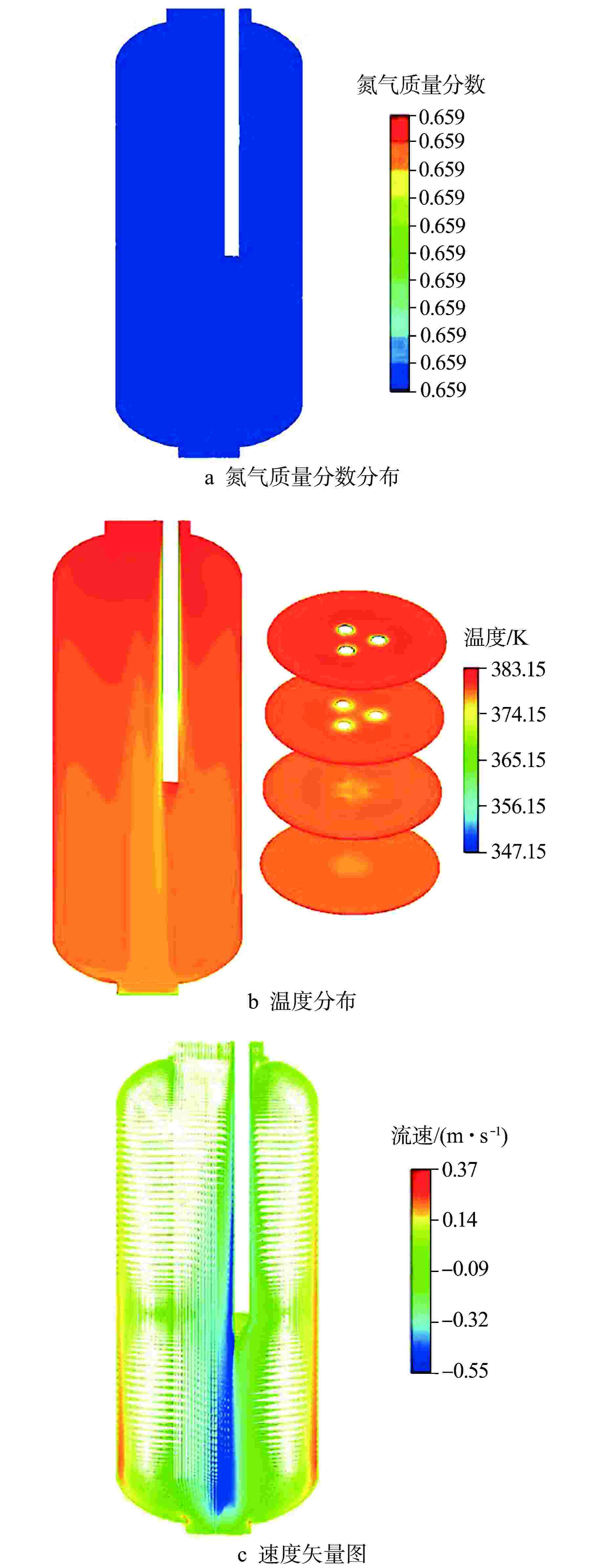
图 3 安全壳模拟体中的各参数分布云图[1]
Figure 3. Distribution Nephogram of Parameters in Containment Simulator
图 4 不同粒径气溶胶的衰减曲线
Figure 4. Attenuation Curves of Aerosols with Different Particle Sizes
图 6 正常工况下安全壳内不同粒径的气溶胶典型轨迹
Figure 6. Typical Trajectories of Aerosols with Different Particle Sizes in Containment under Normal Conditions
-
[1] 肖增光,孙雪霆,陈林林,等. 安全壳内气溶胶沉积试验的浓度测点设计[J]. 核安全,2017, 16(1): 82-85,94. [2] 王雨晴,邓理邻,倪木一,等. 铅铋气溶胶动力学实验平台研制与初步参数测量[J]. 核动力工程,2024, 45(1): 178-185. [3] CLÉMENT B, CANTREL L, DUCROS G, et al. State of the art report on iodine chemistry[Z]. Le Seine Saint-Germain: Organisation for Economic Co-Operation and Development, 2007. [4] 李应治. 池式水洗条件下气溶胶去除特性研究[D]. 哈尔滨: 哈尔滨工程大学,2022. [5] 田家铭,王跃社,李彪,等. 安全壳内放射性气溶胶输运特性模拟研究[J]. 核动力工程,2024, 45(2): 88-95. [6] 彭红花,涂传火,王帅,等. 放射性气溶胶测量腔室内颗粒输运沉积模拟研究[J]. 核技术,2018, 41(11): 5-11. [7] HASTE T, PAYOT F, BOTTOMLEY P D W. Transport and deposition in the Phébus FP circuit[J]. Annals of Nuclear Energy, 2013, 61: 102-121. doi: 10.1016/j.anucene.2012.10.032 [8] MARCH P, SIMONDI-TEISSEIRE B. Overview of the facility and experiments performed in Phébus FP[J]. Annals of Nuclear Energy, 2013, 61: 11-22. doi: 10.1016/j.anucene.2013.03.040 [9] CLÉMENT B, ZEYEN R. The objectives of the Phébus FP experimental programme and main findings[J]. Annals of Nuclear Energy, 2013, 61: 4-10. doi: 10.1016/j.anucene.2013.03.037 [10] CLÉMENT B, HANNIET-GIRAULT N, REPETTO G, et al. LWR severe accident simulation: synthesis of the results and interpretation of the first Phebus FP experiment FPT0[J]. Nuclear Engineering and Design, 2003, 226(1): 5-82. doi: 10.1016/S0029-5493(03)00157-2 [11] GYENES G, AMMIRABILE L. Containment analysis on the PHEBUS FPT-0, FPT-1 and FPT-2 experiments[J]. Nuclear Engineering and Design, 2011, 241(3): 854-864. doi: 10.1016/j.nucengdes.2010.12.007 [12] SCHWARZ M, HACHE G, VON DER HARDT P. PHEBUS FP: a severe accident research programme for current and advanced light water reactors[J]. Nuclear Engineering and Design, 1999, 187(1): 47-69. doi: 10.1016/S0029-5493(98)00257-X [13] DEHBI A. Tracking aerosols in large volumes with the help of CFD[C]//12th International Conference on Nuclear Engineering. Arlington: ASME, 2004: 853-860. [14] 王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社,2004: 78. [15] DEHBI A. Assessment of a new fluent model for particle dispersion in turbulent flows[C]//Workshop on Benchmarking of CFD Codes for Application to Nuclear Reactor Safety (CFD4NRS). Garching: Nuclear Energy Agency of the OECD (NEA), 2006: 703-720. [16] LAURIE M, MARCH P, SIMONDI-TEISSEIRE B, et al. Containment behaviour in Phébus FP[J]. Annals of Nuclear Energy, 2013, 60: 15-27. doi: 10.1016/j.anucene.2013.03.032 [17] JONES A V, ZEYEN R, SANGIORGI M. Circuit and containment aspects of PHÉBUS experiments FPT0 and FPT1[EB/OL].(2015-10-20) [2021-03-15]. http://citeseerx.ist.psu.edu/viewdoc. [18] 江舸航. 安全壳内气溶胶的去除实验研究[D]. 哈尔滨: 哈尔滨工程大学,2023. -
下载:
计量
- 文章访问数: 22
- HTML全文浏览量: 3
- PDF下载量: 4
- 被引次数: 0
