Research on Thermoelectric Coupling Characteristics of a 100 kW Silent Heat Pipe Cooled Reactor Based on Finite Element Method
-
摘要: 静默式热管冷却反应堆(简称热管堆)因其采用高温热管耦合温差发电的能量传输及热电转换系统,具有非能动安全、高可靠、超静音等特点,是未来海陆空天多领域可移动式小型核电源的优选堆型。本文基于多物理场耦合分析平台COMSOL Multiphysics,针对百千瓦级静默式热管堆设计方案,建立了热管堆全系统四分之一模型,包括燃料棒、堆芯基体、热管、反射层、控制棒、滑动反射层、温差发电等系统,开展了稳态工况、单根热管失效工况以及单排热电器件脱载工况下的系统热电耦合特性分析。研究结果表明,由于堆芯基体以及热电系统基体的温度展平特性,单根热管失效不会对反应堆运行以及热电系统输出电功率产生显著影响,热管堆在出现局部热电器件脱载事故时,堆芯温度会因热电系统传热能力下降而升高,未脱载的热电系统仍可以正常工作,保证有效电能输出。Abstract: The silent heat pipe reactor adopts a energy transmission and thermoelectric conversion system that couples high-temperature heat pipes with thermoelectric power generation. It is a preferred reactor type of portable small nuclear power source in various fields such as sea, land, air, and space in the future due to its passive safety, high reliability and ultra silence. Based on the multi physical field coupling analysis platform COMSOL Multiphysics, this paper establishes a quarter model of the whole system of the heat pipe reactor according to the design scheme of a 100-kilowatt level silent heat pipe reactor, including fuel rods, core matrix, heat pipes, reflectors, control rods, sliding reflectors, thermoelectric generations and other systems. Steady-state operating conditions, single heat pipe failure conditions, and single-row thermoelectric system unloading conditions are analyzed to investigate system thermoelectric coupling characteristics. The research results indicate that due to the temperature flattening characteristics of the core matrix and the thermoelectric system matrix, the failure of a single heat pipe will not have a significant impact on the operation of the reactor and the output power of the thermoelectric system. When the local thermoelectric system unloading accident occurs in a heat pipe reactor, the core temperature will increase due to the decrease in the heat transfer capacity of the thermoelectric system. The thermoelectric system that has not been unloaded can still work normally, ensuring effective electrical energy output.
-
0. 引 言
热管冷却反应堆(简称热管堆)依靠热管带走反应堆裂变热,可实现堆本体高度紧凑和较高的可靠性[1]。配合较为成熟的静态热电转换技术,可实现反应堆静默运行[2]。美国先后设计研发了多款热管式核反应堆电源,通常采用碱金属高温热管冷却,根据功率需求的不同,可采用温差发电[3-4]、碱金属转换[5]、斯特林[6]或布雷顿循环[7-8]完成能量转换。美国洛斯阿拉莫斯实验室(LANL)开展的千瓦级裂变核电源Kilopower项目采用钠热管反应堆技术,已完成带核测试,实现满功率运行28 d,具有小型化、模块化、可扩展等技术特点[9]。此外,静默式能量转换技术当前已经较为成熟,在多个领域已经得到应用,我国在器件材料研究方面已具备较好的研究基础。
目前,最具发展潜力、研究最为广泛的一类小型核反应堆电源是采用热管作为热量传递装置的热管堆。与传统反应堆相比,热管堆主要具有以下特点和优势:①具有固态属性,能量传输系统具有非能动特性,固有安全性高;②能量转换系统具有纯静态、静默式的特点,反应堆系统结构简单;③堆芯反应性反馈机制简化,便于自动控制和多模块协同运行;④反应堆系统采用模块化设计思路,灵活性高;⑤结构紧凑,可以拓展应用于不同需求场景。基于以上特性,热管堆在深海装备领域具有巨大的应用价值[10]。
固态热管堆的仿真模拟主要包括一维系统程序和三维多物理耦合分析程序两种手段。WANG C L[11]、ZHANG W W[12]、LIU X[13]等学者通过构建点堆动力学模型、热管热阻网络模型、固体传热模型、静态温差发电模型以及其他辅助模型的方式搭建起热管堆一维系统分析程序,对不同功率等级的热管堆开展了一系列设计分析以及瞬态安全特性分析。ZHANG Z Q[14]等学者对热管模型进行了进一步优化,对百千瓦级和兆瓦级固态热管堆开展了一系列安全特性分析。针对热管堆仿真模拟的三维多物理耦合分析程序分为两大类,一类为外耦合接口多物理场程序:MA Y G[15]等学者利用接口程序耦合了物理分析程序RMC、有限元分析程序ANSYS以及热管分析,实现了热管堆的核-热-力多场耦合分析;另一类为基于统一架构的多物理场耦合平台:TANG S M[16]、ZHANG Y[17]等学者基于多物理场分析平台COMSOL Multiphysics,通过定义偏微分方程组及物理场间的耦合关系,对百千瓦级热管堆开展了核-热-电耦合特性分析。
本文针对百千瓦级静默式热管堆(NUSTER-100)设计方案,基于多物理场耦合分析平台COMSOL Multiphysics,建立了热管堆全系统四分之一模型,包括燃料棒、堆芯基体、热管、反射层、控制棒、滑动反射层、温差发电等系统,开展了稳态工况、单根热管失效工况以及单排热电器件脱载工况下的系统热电耦合响应特性分析。
1. 模型建立
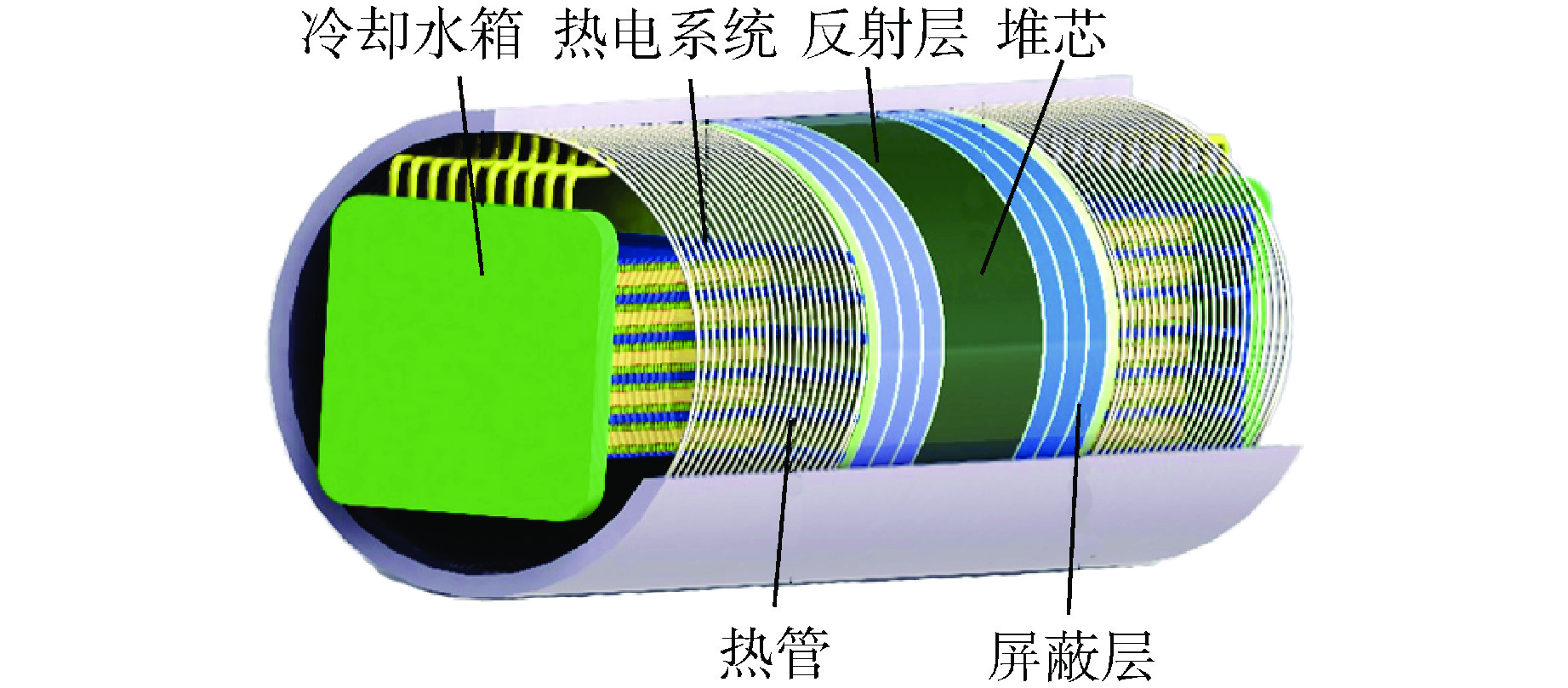
图1展示了一种典型静默式热管堆系统[18],主要由堆芯及其外围两段包裹的反射层、热管以及热电系统构成,总体设计参数如表1所示。
表 1 NUSTER-100热管堆总体设计参数Table 1. Overall Design Parameters of NUSTER-100 Heat Pipe Cooled Reactor参数 数值及类型 反应堆热功率/MW 1 反应堆电功率/kW 100 反应堆寿期/a 5 冷却系统 钠热管 能量转换系统 温差发电器 堆芯活性区体积/L 58.94 热管数目/根 109 燃料棒数目/根 480 富集度/% 73/55/19.75 3种UO2燃料棒数目 332/108/40 活性区基体材料 Mo 上下反射层材料 BeO 滑动反射层/控制棒数目 4/4 滑动反射层/控制棒材料 BeO(不锈钢)/ BeO(B4C) 燃料区外围区域反射层材料 Be 反射层外部材料 B4C 其中,堆芯通常由多个燃料组件紧凑布置成固态基体,并在燃料外围设有控制装置,通过控制棒可以实现对反应堆反应性和功率的调节。燃料组件由数个燃料元件、高温热管和包裹其的基体材料组成,通常也设计成矩阵形式以便实现模块化扩展。整个反应堆中不存在回路式冷却剂,热管冷却反应堆在运行时,堆芯裂变产生的热量通过堆芯基体传递至热管蒸发段,通过热管内部工质的相变过程以及闭式循环实现堆芯冷却,可将热量高效地传递至热电转换系统热端,通过静态热电转换过程实现发电过程,剩余废热通过散热器排至最终热阱。
1.1 高温热管传热模型
由于整堆系统计算量很大,在整堆系统计算中热管使用热阻模型,热管管壁的轴向热阻Rwall为:
$$ R_{\text{wall}}=\frac{\ln(d_0\mathord{\left/\vphantom{d_0d_i}\right.}d\mathrm{_i})}{2\text{π}k_{\text{w}}L_1} $$ (1) 式中,$ {L_1} $为蒸发段长度;$ {d_0} $为管壁外径;$ d\mathrm{_i} $为管壁内径;$ {k_{\text{w}}} $为管壁热导率。
吸液芯区域的轴向热阻Rwick为:
$$ {R_{{\text{wick}}}} = \frac{{\ln ({{{d_{\text{i}}}} \mathord{\left/ {\vphantom {{{d_{\text{i}}}} {{d_{\text{v}}}}}} \right. } {{d_{\text{v}}}}})}}{{2{\text{π}}{k_{{\text{eff}}}}{L_1}}} $$ (2) 式中,$ {d_{\text{v}}} $为吸液芯内径;$ {k_{{\text{eff}}}} $为吸液芯等效热导率。
蒸发段中在气液交界面产生相变带来的热阻Rface为:
$$ {R_{{\text{face}}}} = \frac{{{R_{\text{n}}}T_{\text{v}}^{\text{2}}\sqrt {2{\text{π}}{R_{\text{n}}}{T_{\text{v}}}} }}{{{r^2}p{\text{π}}{d_{\text{v}}}{L_1}}} $$ (3) 式中,$ {R_{\text{n}}} $为蒸汽气体常数;$ r $为汽化潜热;$ p $为蒸汽压力;$ {T_{\text{v}}} $为蒸汽温度。
碱金属气相热阻Rvapor为:
$$ {R_{{\text{vapor}}}} = \frac{{128{L_{{\text{eq}}}}{\mu _{\text{v}}}{T_{\text{v}}}}}{{{\text{π}}d_{\text{v}}^4\rho _{\text{v}}^{\text{2}}{L^2}}} $$ (4) 式中,$ {L_{{\text{eq}}}} $为热管有效长度;$ {\mu _{\text{v}}} $为蒸汽动力粘度;$ {\rho _{\text{v}}} $为蒸汽密度;L为热管的真实长度。
1.2 温差发电模型
热电器件的能量控制方程为:
$$ \rho c_p\frac{\partial T}{\partial t}+\nabla\cdot\left(\alpha TJ\right)-\nabla\cdot\left(k\nabla T\right)=s $$ (5) 式中,$ \rho $为热电材料的密度;$ T $为热电材料的温度;$ c_p $为比热容;$ \alpha $为塞贝克系数;$ J $为电流密度;$ k $为热导率;$ s $为发热量。
电场控制方程为:
$$ J = \frac{1}{{{\rho _{\text{e}}}}}\left( {E - \alpha \nabla T} \right) $$ (6) 式中,$ E $为电场强度;ρe为电阻率。
由电流守恒可得:
$$ \nabla \cdot J = - \nabla \cdot \left( {\frac{{\nabla \varphi }}{{{\rho _{\text{e}}}}}} \right) - \nabla \cdot \left( {\frac{{\alpha \nabla T}}{{{\rho _{\text{e}}}}}} \right){\text{ = }}0 $$ (7) 式中,$ \varphi $为标量电位。
高温热管和温差发电通过热流密度耦合,通过热电器件的热流密度q为:
$$ q = \alpha TJ - k\nabla T $$ (8) 热-电耦合控制方程为:
$$ \nabla\cdot\left(k\nabla T\right)+\frac{J^2}{\sigma}-TJ\cdot\left[\left(\frac{\partial\alpha}{\partial T}\right)\nabla T+\left(\nabla\alpha\right)\right]=0 $$ (9) 三级梯联热电器件依次由低温碲化铋材料、中温方钴矿材料以及高温半赫斯勒材料(HH)串联组成,其热电物性如下:
低温区域采用的是碲化铋热电材料:N极热电材料为Bi2Te2.7Se0.3,P极热电材料为Bi0.5Sb1.5Te3。
N极热电材料塞贝克系数αBiTe-n为:
$$ \begin{split} {\alpha _{{\text{BiTe-n}}}} = & 1.71 \times {10^{ - 3}} - 1.523 \times {10^{ - 5}}T + 3.76 \times {10^{ - 8}}{T^2}- \\ & 2.915 \times {10^{ - 11}}{T^3} \\[-1pt] \end{split} $$ (10) P极热电材料塞贝克系数αBiTe-p为:
$$ \begin{split} {\alpha _{{\text{BiTe-p}}}} =& - 4.236 \times {10^{ - 3}} + 3.5823 \times {10^{ - 5}}T - \\ & 1.036 \times {10^{ - 7}}{T^2} + 1.257 \times {10^{ - 10}}{T^3} \end{split} $$ (11) 中温区域匹配的是方钴矿热电材料:N极热电材料为Yb0.3Co4Sb12,P极热电材料为CeFe3CoSb12。
N极热电材料塞贝克系数αn-skt为:
$$ \begin{split} {\alpha _{{\text{n-skt}}}} =& 3.18 \times {10^{ - 6}} - 6.88 \times {10^{ - 7}}T + \\ & 1.48 \times {10^{ - 9}}{T^2} - 1.92 \times {10^{ - 12}}{T^3} \end{split} $$ (12) P极热电材料塞贝克系数αp-skt为:
$$ \begin{split} {\alpha _{{\text{p-skt}}}} = & - 2.74 \times {10^{ - 5}} + 5.48 \times {10^{ - 7}}T - \\ & 4.1 \times {10^{ - 10}}{T^2} + 4.3 \times {10^{ - 14}}{T^3} \end{split} $$ (13) 高温区域采用的是HH:N极材料为ZrNiSn,P极材料为ZrCoSb。
N极热电材料塞贝克系数为:
$$ \begin{split} {\alpha _{{\text{HH-n}}}} = & 3.658 \times {10^{ - 5}} - 4.04 \times {10^{ - 7}}T + \\ & 2.472 \times {10^{ - 10}}{T^2} \end{split} $$ (14) P极热电材料塞贝克系数为:
$$ \begin{split} {\alpha _{{\text{HH-p}}}} = & 1.576 \times {10^{ - 5}} + 2.616 \times {10^{ - 7}}T - \\ & 8.109 \times {10^{ - 11}}{T^2} \end{split} $$ (15) 1.3 其他模型
燃料棒功率分布通过蒙卡程序MCNP计算获得,作为热源输入边界。
燃料芯块内节点的控制方程为:
$$ {\rho _{\text{U}}}{c_{\text{U}}}\frac{{\partial {T_{\text{U}}}}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {{k_{\text{U}}}r\frac{{\partial {T_{\text{U}}}}}{{\partial r}}} \right) + {Q_{\text{V}}} $$ (16) 式中,${\rho _{\text{U}}}$为燃料芯块的密度;${c_{\text{U}}}$为燃料芯块的比热;${T_{\text{U}}}$为燃料芯块的温度;${k_{\text{U}}}$为燃料芯块的导热系数;${Q_{\text{V}}}$为燃料控制体的热源密度。
包壳控制衡方程为:
$$ \begin{split} \rho_{\text{C}}c_{\text{C}}\frac{\partial T_{\text{C}}}{\partial t}= & A_{\text{Ci}}\left[\varepsilon_{\text{C}}\sigma(T_{\text{U}}^{\text{4}}-T_{\text{C}}^{\text{4}})+\frac{k_{\text{G}}}{\delta_{\text{G}}}(T_{\text{U}}-T_{\text{C}})\right]- \\ &A_{\text{Co}}\frac{k_{\text{M}}}{\delta_{\text{M}}}\left(T_{\mathrm{C}}-T_{\text{M}}\right) \end{split} $$ (17) 式中,${T_{\text{M}}}$为基体的温度;$ {k_{\text{M}}} $为基体的热导率;${\delta _{\text{M}}}$为基体厚度;$ A_{\text{Ci}} $和$ A_{\text{Co}} $为包壳的内表面和外表面面积;下标C表示包壳。
基体导热热平衡方程为:
$$ \rho_{\text{M}}c_{\text{M}}\frac{\partial T_{\text{M}}}{\partial t}=A_{\text{Mi}}\frac{k_{\text{M}}}{\delta_{\text{M}}}(T_{\text{C}}-T_{\text{M}})-A_{\text{Mo}}\frac{k_{\text{h}}}{\delta_{\text{h}}}\left(T_{\text{M}}-T_{\text{hp}}\right) $$ (18) 式中,${T_{{\text{hp}}}}$为热管管壁的温度;${k_{\text{h}}}$为热管管壁的热导率;${\delta _{\text{h}}}$为热管管壁厚度;$ {A_{{\text{Mi}}}} $和$ {A_{{\text{Mo}}}} $为基体的内表面和外表面面积;下标M表示基体。
2. 模型验证
为了验证热电耦合分析平台的准确性以及适用性,本文利用开发的高温热管及温差发电器多物理场耦合分析平台对搭建的原理样机进行建模仿真,并与传热及热电转换实验数据进行对比。
如图2所示为原理样机实物图,实验装置采用6根电加热棒模拟堆芯燃料棒,通过电加热形式模拟堆芯燃料产热,热管采用7根高温钾热管,用于实现非能动热量传输功能,高温热管参数如表2所示。高温热管与加热棒通过紫铜基体连接,模拟热管堆中燃料棒与热管之间通过基体导热过程;利用同为碱金属热管、传热性能相似的钾热管模拟热管堆中高温钠热管的非能动传热特性;利用与钾热管运行温度区间相匹配的方钴矿温差发电器实现热电转换功能。数值模型几何的网格划分如图3所示。联立热管传热、温差发电以及固体导热等方程,利用COMSOL Multiphysics求解器求解。具体而言,电加热棒、铜块和热管壁的传热采用固体传热模型,热管中钾液体和蒸汽的流动传热过程采用流体传热模块实现,热管蒸汽区域的蒸汽流动采用层流模型,热管吸液芯区域的钾液体流动采用Darcy流模型,吸液芯区域采用多孔介质模型进行建模,热电模块用于计算热电转换过程,AC/DC模块与热电模块连接以获取热电器件的外部负载特性,在电加热棒中输入体积热源,热电器件与冷却水板的冷却边界采用强制对流传热模型。数值模型网格划分采用四面体网格,对不同部件之间接触面以及热电器件进行局部加密处理。
表 2 高温热管参数Table 2. Parameters of High Temperature Heat Pipe参数 数值及类型 工质 钾 热管类型 吸液芯 热管管壳材质 304不锈钢 热管工质充液量/g 20 外径/mm 28 长度/mm 800 (蒸发段/绝热段/冷凝段长度)/mm 200/150/250 内径/mm 22 吸液芯目数 300 2.1 传热特性验证
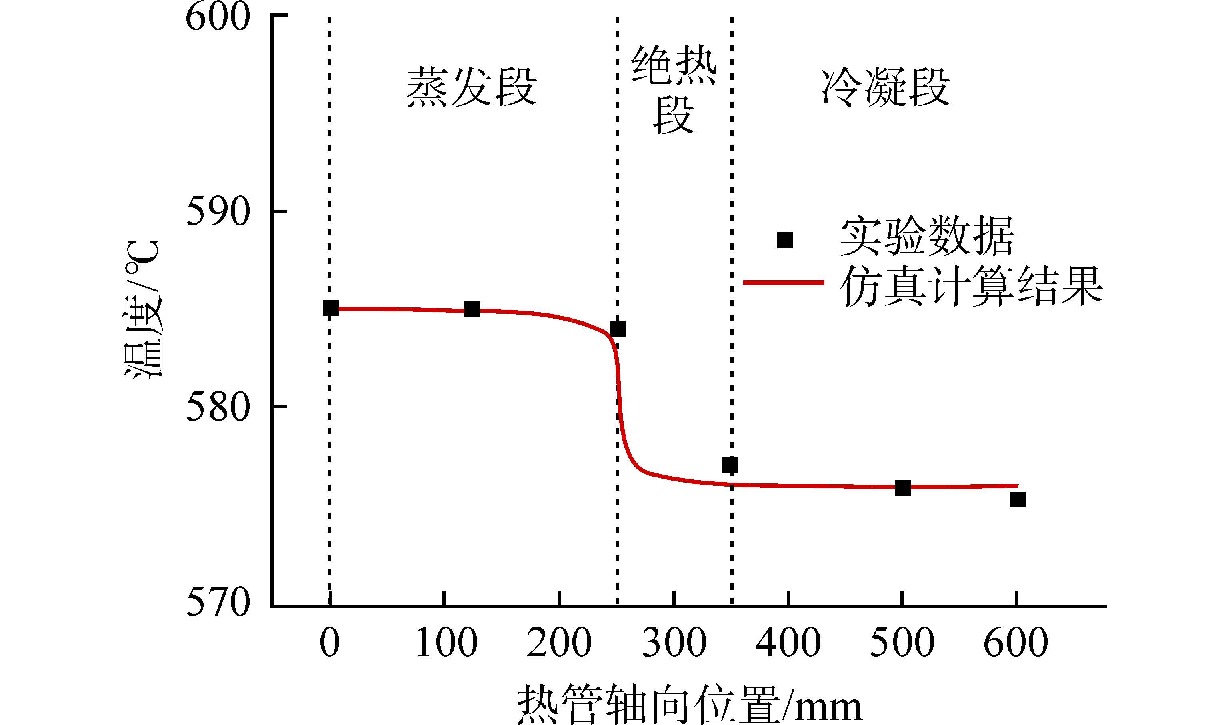
图4为热管传热特性数值模拟结果与实验数据的对比,重点对比了稳态工况下热管蒸发段、冷凝段的温度分布情况。数值模拟结果与实验数据符合良好,验证了高温热管传热模型的可靠性,模型可用于热管堆的系统安全特性计算分析。
2.2 热电特性验证
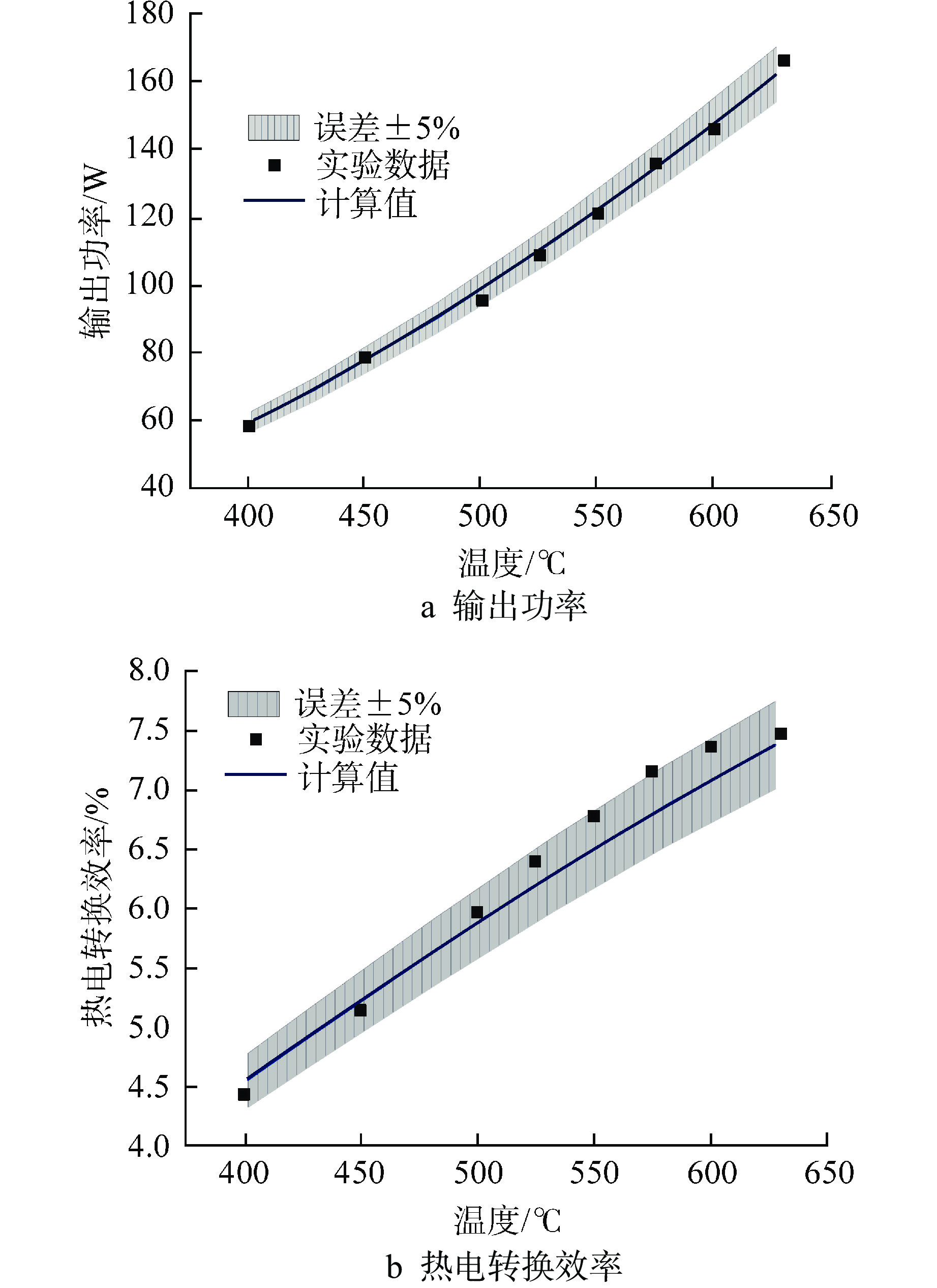
图5展示的是实验装置中10组温差发电器输出热电性能随温度变化的数值模拟计算值与实验数据的对比。其中图5a展示的是热电系统输出功率随热端温度的变化情况,图5b展示的是热电系统热电转换效率随热端温度的变化情况。计算值与实验数据符合良好,可以看出针对实验装置热电系统建立的数值模型可以准确模拟其热电输出性能。通过原理样机实验数据验证,证明了开发的热电模型的准确性及适用性。
3. 热电及安全特性
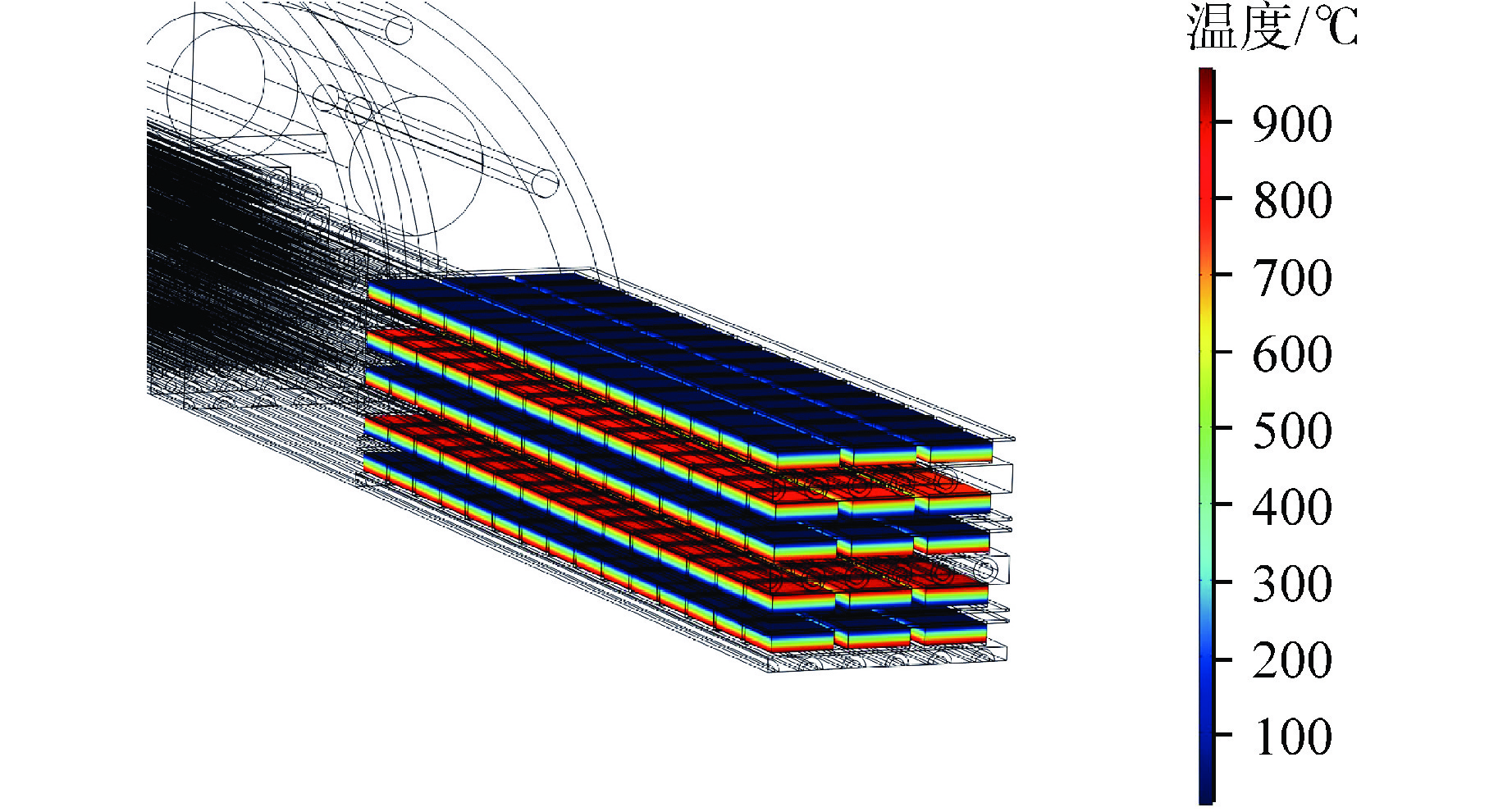
由于NUSTER-100结构的对称性,利用有限元分析软件COMSOL Multiphysics建立1/4模型。该模型包括燃料棒、堆芯基体、热管、反射层、控制棒、滑动反射层和热电系统。热场和电场通过温度相关参数耦合。燃料棒的体积功率密度设置为热功率边界条件,集成的外部电路连接到热电转换系统用以模拟系统负载跟随特性,对称平面设置对称边界条件,除冷却水板外,仿真模型的外边界使用绝热边界条件。模型采用四面体网格进行网格划分,并在不同部件的接触面上进行局部网格细化,以提高网格质量和收敛性。NUSTER-100仿真模型的几何模型和网格划分分别如图6和图7所示。
3.1 稳态工况
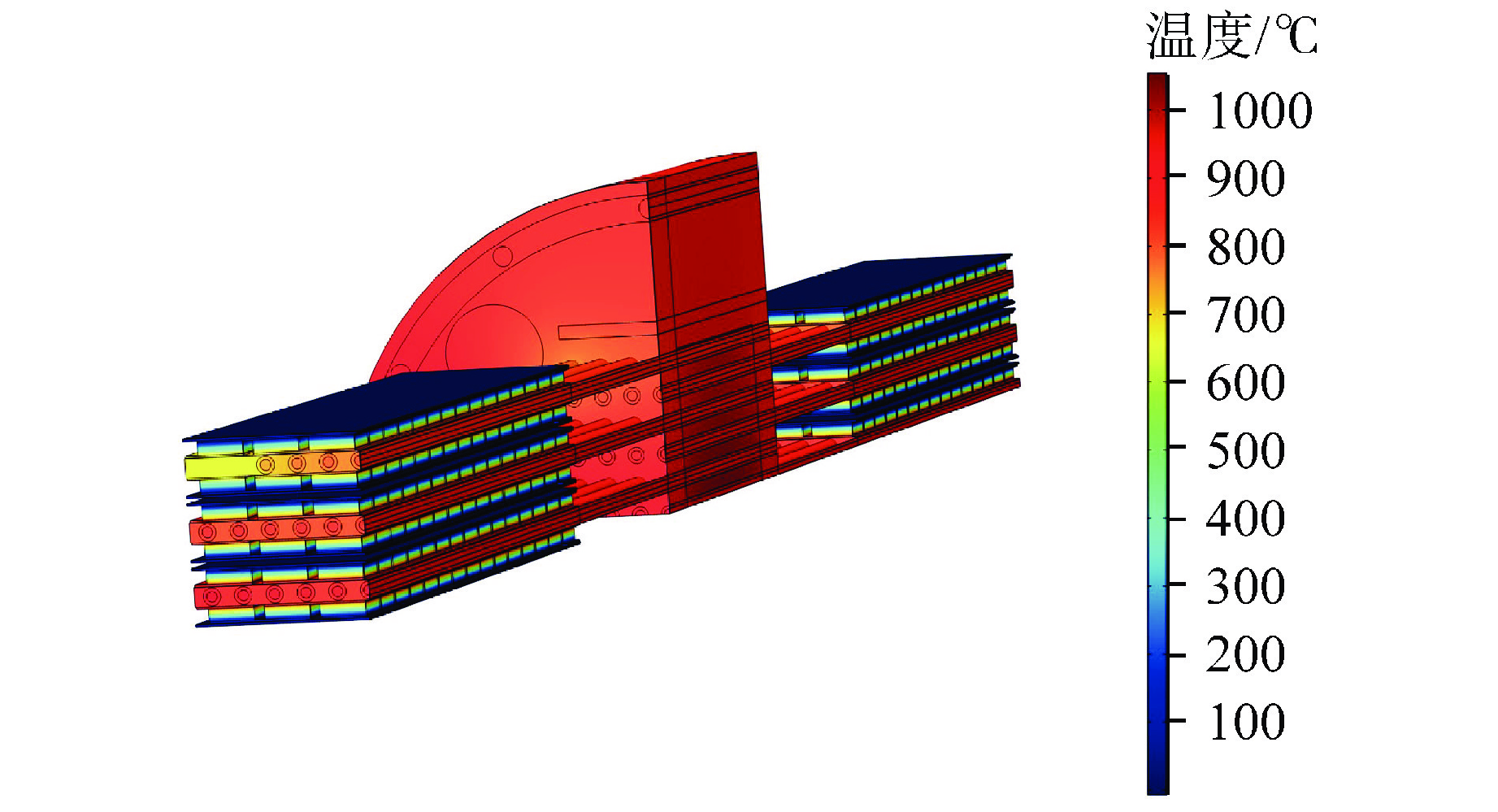
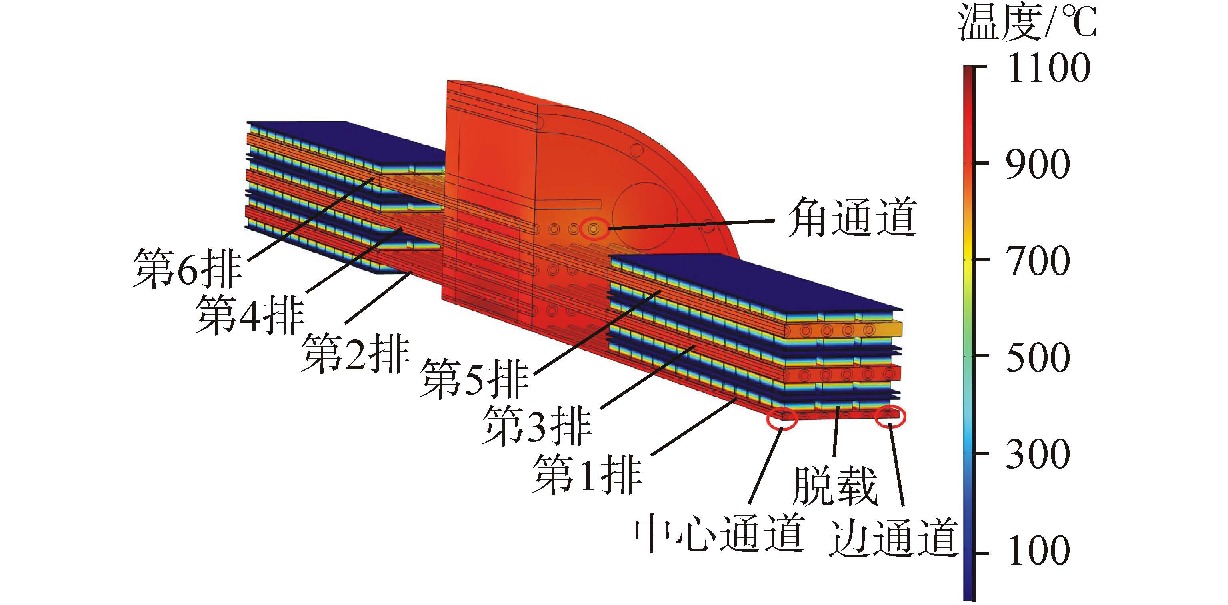
图8所示的是稳态工况下NUSTER-100的整体温度分布。由于热电材料的热阻远大于其他组件材料的热阻,因此在热电系统冷热端两侧之间的温度梯度可达853.2℃。基体的最高温度为1052.3℃,燃料棒最高温度1312.2℃出现在中心燃料棒中心位置处,堆芯基体的平均温度为906.8℃。由于热管对应的燃料棒数量以及功率分布的不同,各个热管的传热功率以及运行温度也有所不同,堆中热管的运行温度分布在712.3~1022.5℃。热管具有良好的等温性和传热性能,可以实现堆芯的有效冷却。热管冷凝段通过基体集成,一方面具有温度展平的作用,另一方面可以为热电系统提供平整的安装平面。由于最外侧热管数量布置较少,因此最外侧热电系统热端温度相对较低,热电系统热端温度分布在685.2~923.6℃,可为热电系统提供足够的热流密度。热电系统冷端通过冷却水强制对流冷却,温度可保持在20.0℃。反应堆堆芯温度在800.0℃以上运行,高于常规反应堆的运行温度,因此堆芯各部件的高温机械性能对于热管堆堆芯的安全特性意义重大。
图9所示为燃料棒的轴向功率分布。图10所示为燃料棒的径向功率分布。堆芯轴向两端和径向外围分别布置有反射层,由于堆芯周围反射层的中子反射效应以及燃料富集度的不同,反射层附近燃料棒的功率密度高于中心区域燃料棒的功率密度。
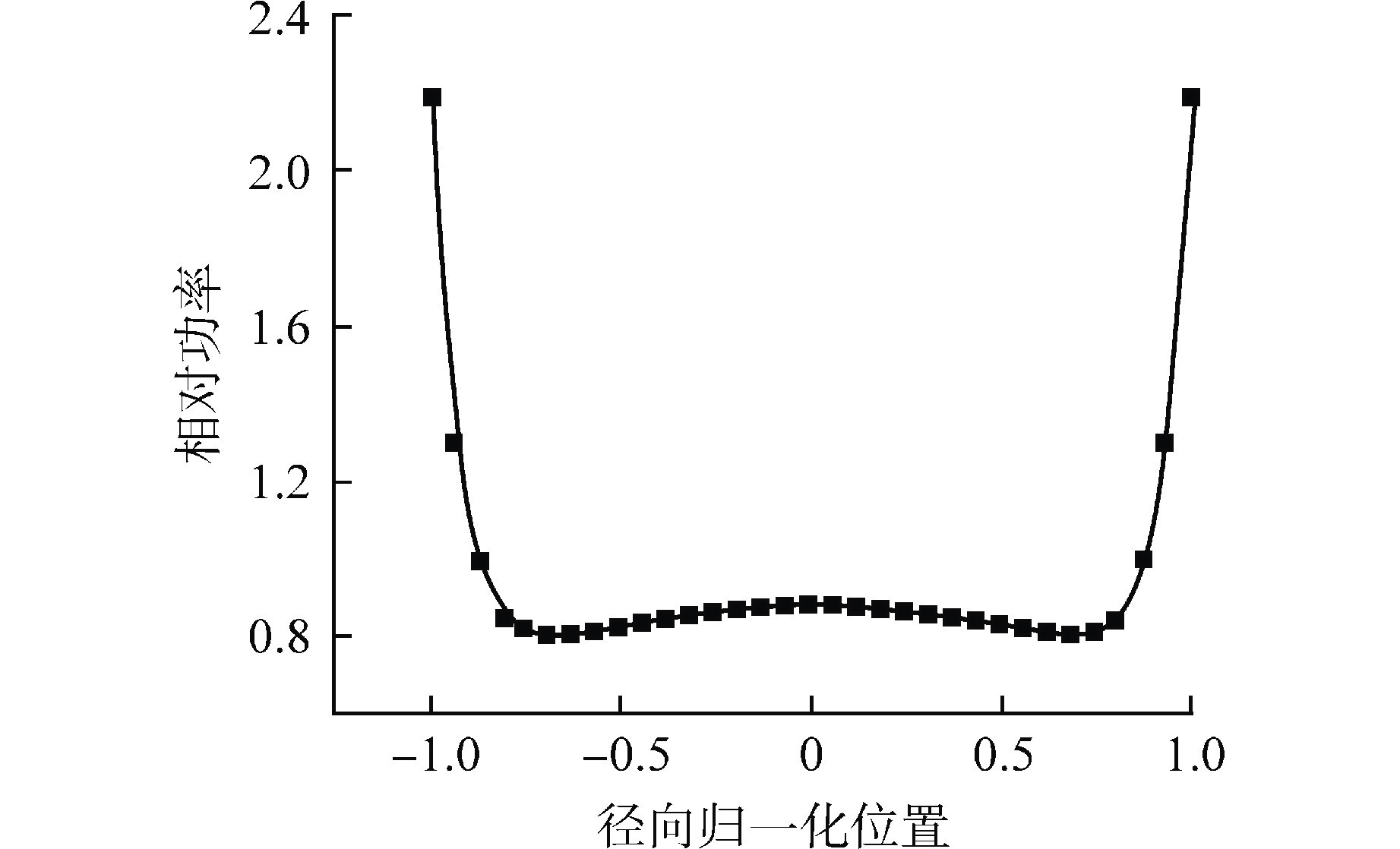
燃料棒功率密度分布在2.87×107~1.13×108 W·m−3。由于轴向反射层的中子反射效应,轴向相对功率分布呈W形。由于堆芯在轴向方向呈对称结构,因此燃料棒功率密度在轴向方向也呈对称分布。相对功率因子最小值为0.87,出现在距离堆芯中心对称面17.8 cm位置处,相对因子最大值为1.082,出现在燃料棒的两端,堆芯中心对称面处相对功率因子为1.071。
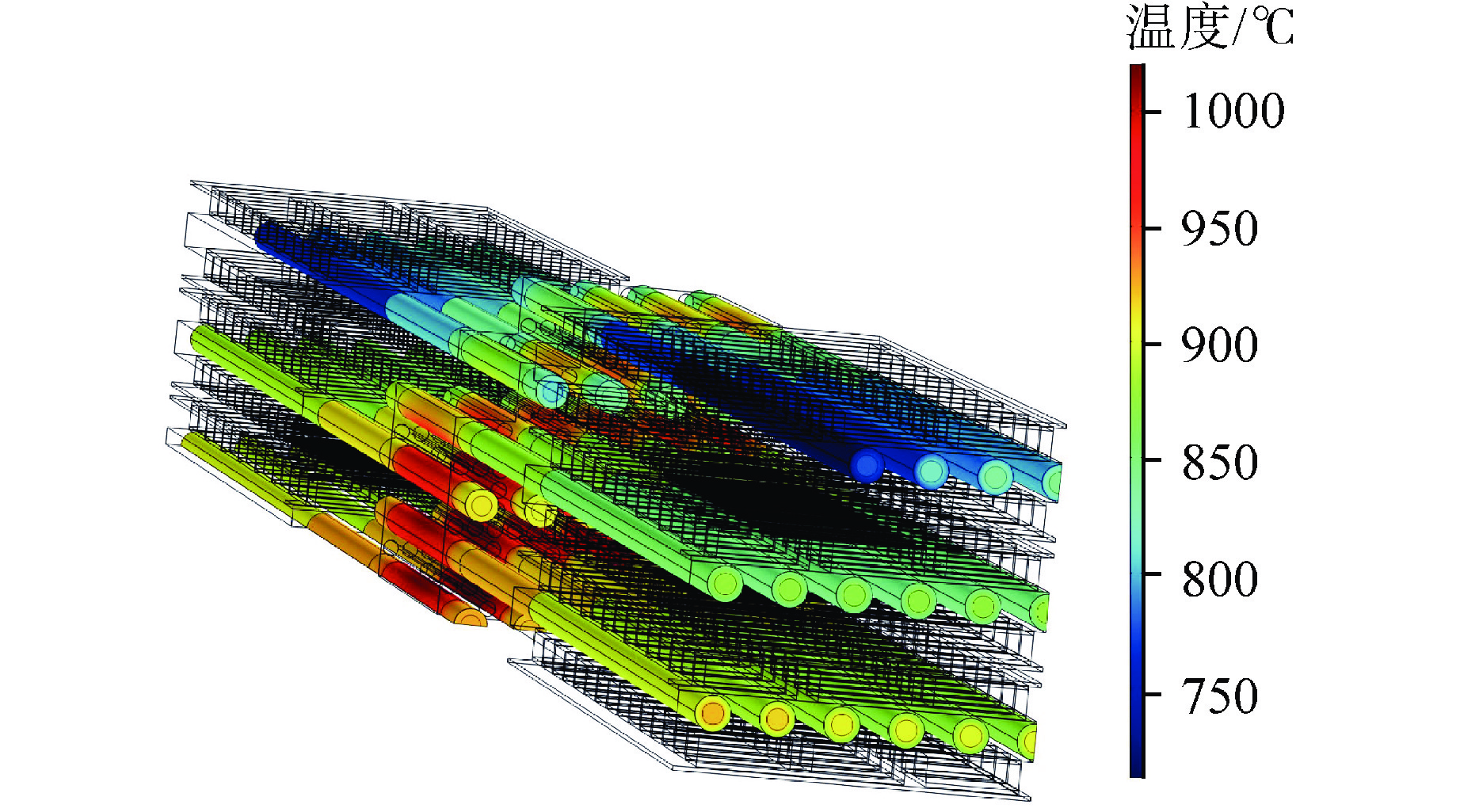
高温热管的温度分布如图11所示。热管的工作温度由堆芯温度以及热电系统温度共同决定。由于堆芯基体和用于连接热管及热电系统的基体的温度展平综合作用,同一排热管的温度分布相似。单根热管蒸发段和冷凝段之间温度梯度稳定在110.0℃左右。热管冷凝段温度分布在710.0~885.0℃,与高性能三段式热电器件的工作温度区间相匹配。
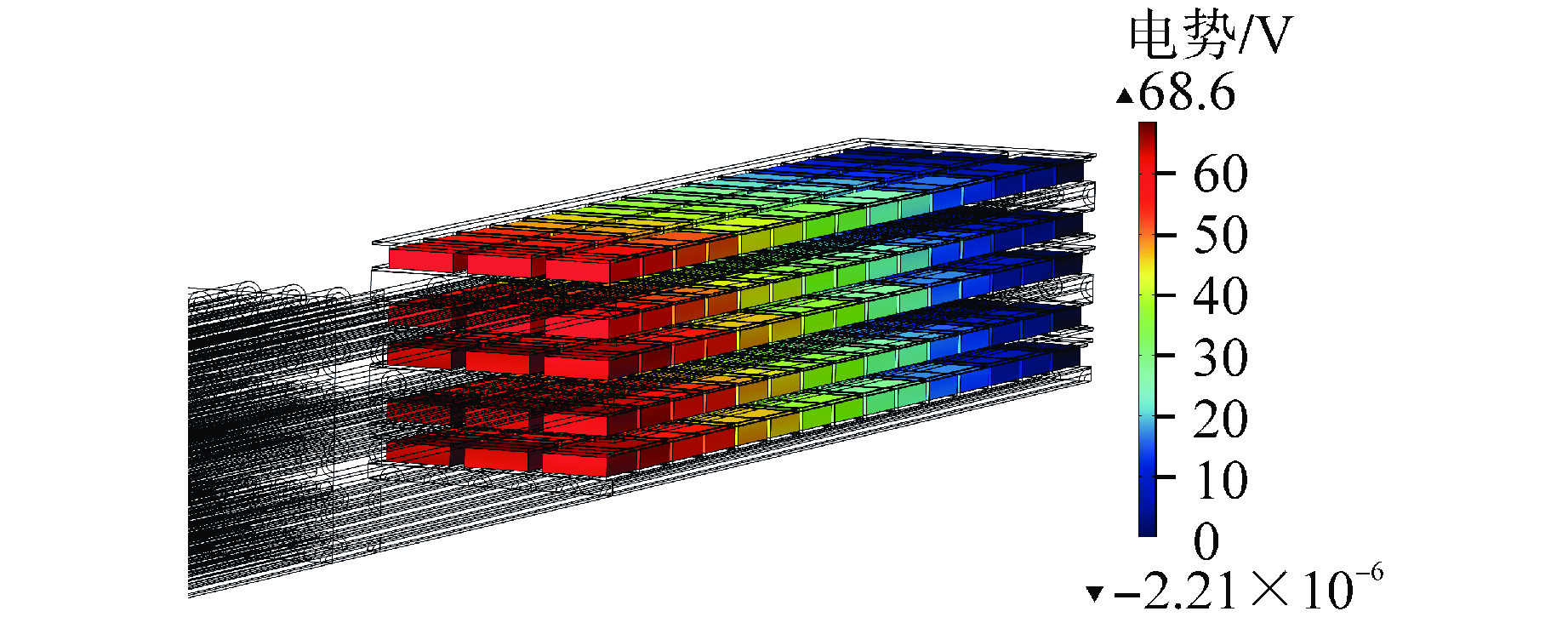
热电系统匹配外部负载时的电势分布如图12所示。同一排的热电器件以串联的方式连接外部负载,不同排的热电器件分别连接到独立的外部负载,用于观察每一排热电系统的详细输出特性。闭合电路的接地端均设置在位于热管冷凝段末端处的热电器件端口,不同排之间热管数量以及热管传递的热量有所不同,不同排之间热电系统电势分布趋势虽一致,但端口输出电压以及输出功率仍存在一定差异。不同排之间的热电系统输出电压分布在58.3~69.1 V,回路电流分布在40.1~57.6 A,输出功率分布在2.3~3.3 kW。NUSTER系统总输出功率为123.2 kW,系统热电转换效率为12.3%。不同排的热电系统可以根据具体的任务需求灵活串联或并联。
3.2 中心单根热管失效工况
图13所示为热管堆中心单根热管失效工况下的系统温度分布。由于失效热管丧失了高效的传热性能,热管失效工况会引起失效热管随连接的堆芯温度升高,该工况下堆芯基体最高温度为1063.8℃,相比于稳态工况最高温度升高11.5℃。失效热管随连接的热电器件热端输入热流密度和温度降低,会进一步影响热电器件的局部输出特性。热管失效引起的温度变化主要是局部效应,由于堆芯基体以及热电系统热端基体的温度展平效应,热管失效不会引起其周围燃料棒的包壳破损及燃料熔化的风险,失效热管周围的热量会通过基体导热传递至周围其他热管,进而实现堆芯有效冷却。
图14所示是热管堆中心单根热管失效工况下堆芯燃料棒包壳温度分布。不同位置处燃料棒功率密度分布以及对应的热管传热能力不同,燃料棒包壳温度由中心位置向边角方向逐渐降低,温度分布区间为879.8~1099.5℃。由于中间通道所对应热管失效,其导热能力基本丧失,无法直接带走其周围燃料棒产生的热量,因此中心通道位置处堆芯温度升高,其对应燃料芯块最高温度达1361.8℃,比稳态工况升高49.6℃。失效热管所对应位置处燃料棒释放的热量可被其周围热管有效带走,因此其他通道所对应的堆芯温度未发生显著变化。
图15所示为热管堆中心单根热管失效工况下热管温度分布。由于中间通道所对应热管失效,热管等温性明显变差,其蒸发段平均温度为1079.4℃,蒸发段前端和末端内置于轴向反射层,使得蒸发段前端和末端温度未出现显著升高。失效热管无法通过内部工质的相变和闭式循环高效传热,仅依靠热管管壁和吸液芯的导热传热,因此其绝热段也无法保持均匀的温度分布,绝热段温度梯度达168.1℃。其冷凝段内置于基体中,由于基体良好的导热性能以及温度展平作用,因此冷凝段温度梯度较小,仅为42.6℃。由于失效热管冷凝段温度分布主要取决于冷凝段基体加热,其冷凝段温度最低达到868.7℃。
图16所示是热管堆中心单根热管失效工况下热电系统一侧的电势分布。由于堆芯基体良好的导热性能,失效热管周围的燃料棒释放的热量可以通过堆芯基体传递至其附近的热管,热管冷凝段释放的热量通过热电系统热端布置的基体收集起来并传递至热电器件热端,因此对于热电系统来说,局部热管失效不会引起热电系统剧烈的热电性能变化。在单根热管失效工况下,热电系统仍可以正常运行,热电系统输出电压最大为68.6 V,与稳态数据相当。该工况下整堆热电系统输出功率仍可达122.1 kW,整堆热电转换效率仍可达12.2%。
3.3 单排热电器件脱载工况
热电器件脱载工况是指由于热电器件损坏或者与外部负载连接断开造成的运行事故工况,局部热电器件脱载会造成局部热电系统的电输出丧失,并会引起热电系统局部传热性能的改变,进而影响系统的安全特性。
图17所示的是单排热电器件脱载工况下热管堆系统温度分布图。为了便于表述,将图17中热管自下向上依次升序排列,分别标注为第1排~第6排。发生脱载工况的是位于堆芯中心位置的第1排热管随连接的一排热电器件。
相比于稳态条件下的热管堆系统温度分布,单排热电器件脱载工况会引起堆芯温度的整体升高。该工况下包括燃料棒、基体以及热管蒸发段在内的堆芯温度均超过了800.0℃,基体的最高温度为1103.5℃,燃料棒最高温度为1371.7℃,比稳态工况下的最高温度高59.5℃。由于第5排和第6排热管的数量分别为4根和3根,比其他排少1根和2根,并且第5排和第6排所对应堆芯区域燃料棒数量少,堆芯传递至第5排和第6排的总热量相比于其他排的热管更少,热电系统布置的热电器件数量相同,因此第5排和第6排热管对于堆芯的冷却效果更好,第5排和第6排的整体温度分布相比于其他排低。
图18所示是单排热电器件脱载工况下热管以及堆芯的温度分布。高温热管温度分布由堆芯燃料棒功率密度以及热电系统传热特性共同决定。由于第1排热管连接的热电器件发生脱载工况,该排热电器件传热性能降低,因此第1排热管整体温度最高,蒸发段温度为1051.5℃,冷凝段温度为960.3℃。由于堆芯基体以及热电系统热端基体的温度展平效应,同一排的热管温度分布一致。自第1排开始,热管温度随着排数的升高逐渐降低。热管冷凝段温度直接决定了热电系统的热端热流密度,进而决定了热电系统的热电转换性能,因此对于各排热管所连接的热电系统,随着热管所在排数的升高,对应的热电系统热电转换性能逐渐降低。边、中心通道所在位置处热管蒸发段温度分别为1051.5℃和998.7℃,因所连热电器件脱载导致整体运行温度分别升高40.0℃和34.4℃。角通道所在位置处热管运行温度未发生显著变化。
图19所示为单排热电器件脱载工况下热电系统的温度分布。热电器件为热管堆中最大的热阻,直接决定了热管堆堆芯以及热管的运行温度,同时热管的传热性能也决定了热电器件的热端输入热流密度,决定了热电器件所建立的温度梯度,进而决定热电器件的热电输出特性。对于第1排热管对应的热电器件,由于发生热电器件脱载工况,温度梯度相比于其他热电器件更大,温度梯度可达965.8℃,而第3排和第5排热管所对应的热电器件建立的平均温度梯度分别为848.4℃和794.1℃。
图20所示为单排热电器件脱载工况下热电系统的电势分布。由于第1排热电器件脱载,无输出电特性,该排热电系统处于断路状态,因此第1排热电器件的输出端口电压为开路电压114.0 V。其他排的热电器件运行正常,输出端口电压为电回路中的输出电压,自下向上,随着热管排数的升高,所对应的热电器件输出电压逐渐降低,第3排和第5排的热电器件输出电压分别为59.1 V和52.1 V,输出电流分别为52.2 A和48.3 A,输出功率分别为3085.0 W和2530.9 W。在该工况下,整堆热电系统输出功率为119.1 kW,整堆热电转换效率仍可达11.91%。
4. 结 论
本文针对百千瓦级静默式热管堆设计方案,基于多物理场耦合分析平台COMSOL Multiphysics,建立了热管堆全系统四分之一模型,构建了高温热管传热模型、温差发电模型以及堆芯传热等核心模型,利用热管耦合温差发电器原理样机实验数据对数值方法进行了验证。研究结果表明,由于堆芯基体以及热电系统基体的温度展平特性,单根热管失效不会对反应堆运行以及热电系统输出电功率产生显著影响,整堆热电系统输出功率仍可达122.1 kW,整堆热电转换效率仍可达12.2%。热管堆在出现局部热电器件脱载事故时,堆芯温度会因热电系统传热能力下降而升高,未脱载的热电系统仍可以正常工作,保证有效电能输出,整堆热电系统输出功率为119.1 kW,整堆热电转换效率仍可达11.91%。
-
表 1 NUSTER-100热管堆总体设计参数
Table 1. Overall Design Parameters of NUSTER-100 Heat Pipe Cooled Reactor
参数 数值及类型 反应堆热功率/MW 1 反应堆电功率/kW 100 反应堆寿期/a 5 冷却系统 钠热管 能量转换系统 温差发电器 堆芯活性区体积/L 58.94 热管数目/根 109 燃料棒数目/根 480 富集度/% 73/55/19.75 3种UO2燃料棒数目 332/108/40 活性区基体材料 Mo 上下反射层材料 BeO 滑动反射层/控制棒数目 4/4 滑动反射层/控制棒材料 BeO(不锈钢)/ BeO(B4C) 燃料区外围区域反射层材料 Be 反射层外部材料 B4C 表 2 高温热管参数
Table 2. Parameters of High Temperature Heat Pipe
参数 数值及类型 工质 钾 热管类型 吸液芯 热管管壳材质 304不锈钢 热管工质充液量/g 20 外径/mm 28 长度/mm 800 (蒸发段/绝热段/冷凝段长度)/mm 200/150/250 内径/mm 22 吸液芯目数 300 -
[1] GUO K L, ZHANG Y, LIN X Y, et al. Transient thermoelectric characteristics of the principle prototype for the heat pipe cooled nuclear Silent themoelectirc reactor (NUSTER)[J]. Annals of Nuclear Energy, 2023, 189: 109818. doi: 10.1016/j.anucene.2023.109818 [2] SUN H, MA P, LIU X, et al. Conceptual design and analysis of a multipurpose micro nuclear reactor power source[J]. Annals of Nuclear Energy, 2018, 121: 118-127. doi: 10.1016/j.anucene.2018.07.025 [3] TANG S M, LIU X, WANG C L, et al. Thermal-electrical coupling characteristic analysis of the heat pipe cooled reactor with static thermoelectric conversion[J]. Annals of Nuclear Energy, 2022, 168: 108870. doi: 10.1016/j.anucene.2021.108870 [4] TANG S M, WANG C L, ZHANG D L, et al. Thermoelectric performance study on a heat pipe thermoelectric generator for micro nuclear reactor application[J]. International Journal of Energy Research, 2021, 45(8): 12301-12316. doi: 10.1002/er.6450 [5] PETERSON P F. Multiple-reheat Brayton cycles for nuclear power conversion with molten coolants[J]. Nuclear Technology, 2003, 144(3): 279-288. doi: 10.13182/NT144-279 [6] DAI Z W, WANG C L, ZHANG D L, et al. Design and analysis of a free-piston stirling engine for space nuclear power reactor[J]. Nuclear Engineering and Technology, 2021, 53(2): 637-646. doi: 10.1016/j.net.2020.07.011 [7] WANG C L, ZHANG R, GUO K L, et al. Dynamic simulation of a space gas-cooled reactor power system with a closed Brayton cycle[J]. Frontiers in Energy, 2021, 15(4): 916-929. doi: 10.1007/s11708-021-0757-9 [8] ZHANG R, GUO K L, WANG C L, et al. Thermal-hydraulic analysis of gas-cooled space nuclear reactor power system with closed Brayton cycle[J]. International Journal of Energy Research, 2021, 45(8): 11851-11867. doi: 10.1002/er.5813 [9] MCCLURE P R, POSTON D I, GIBSON M A, et al. Kilopower project: the KRUSTY fission power experiment and potential missions[J]. Nuclear Technology, 2020, 206(S1): S1-S12. [10] 余红星,马誉高,张卓华,等. 热管冷却反应堆的兴起和发展[J]. 核动力工程,2019, 40(4): 1-8. [11] WANG C L, SUN H, TANG S M, et al. Thermal-hydraulic analysis of a new conceptual heat pipe cooled small nuclear reactor system[J]. Nuclear Engineering and Technology, 2020, 52(1): 19-26. [12] ZHANG W W, ZHANG D L, WANG C L, et al. Conceptual design and analysis of a megawatt power level heat pipe cooled space reactor power system[J]. Annals of Nuclear Energy, 2020, 144: 107576. doi: 10.1016/j.anucene.2020.107576 [13] LIU X, ZHANG R, LIANG Y, et al. Core thermal-hydraulic evaluation of a heat pipe cooled nuclear reactor[J]. Annals of Nuclear Energy, 2020, 142: 107412. doi: 10.1016/j.anucene.2020.107412 [14] ZHANG Z Q, CHAI X M, WANG C L, et al. Numerical investigation on startup characteristics of high temperature heat pipe for nuclear reactor[J]. Nuclear Engineering and Design, 2021, 378: 111180. doi: 10.1016/j.nucengdes.2021.111180 [15] MA Y G, LIU J S, YU H X, et al. Coupled irradiation-thermal-mechanical analysis of the solid-state core in a heat pipe cooled reactor[J]. Nuclear Engineering and Technology, 2022, 54(6): 2094-2106. doi: 10.1016/j.net.2022.01.002 [16] TANG S M, LIAN Q, ZHU L X, et al. Thermal-electrical coupling analysis of the static heat pipe cooled reactor under heat pipe failure condition[J]. Nuclear Engineering and Design, 2024, 417: 112812. doi: 10.1016/j.nucengdes.2023.112812 [17] ZHANG Y, GUO K L, WANG C L, et al. Numerical analysis of segmented thermoelectric generators applied in the heat pipe cooled nuclear reactor[J]. Applied Thermal Engineering, 2022, 204: 117949. doi: 10.1016/j.applthermaleng.2021.117949 [18] HUANG J L, WANG C L, TIAN Z X, et al. Preliminary conceptual design and analysis of a 100 kWe level Nuclear Silent Thermal-Electrical Reactor (NUSTER-100)[J]. International Journal of Energy Research, 2022, 46(14): 19653-19666. doi: 10.1002/er.8542 -







 下载:
下载:




















 下载:
下载: