Research on Parameter Prediction for Transient Conditions in Rod Bundle Subchannel Based on POD-ML Method
-
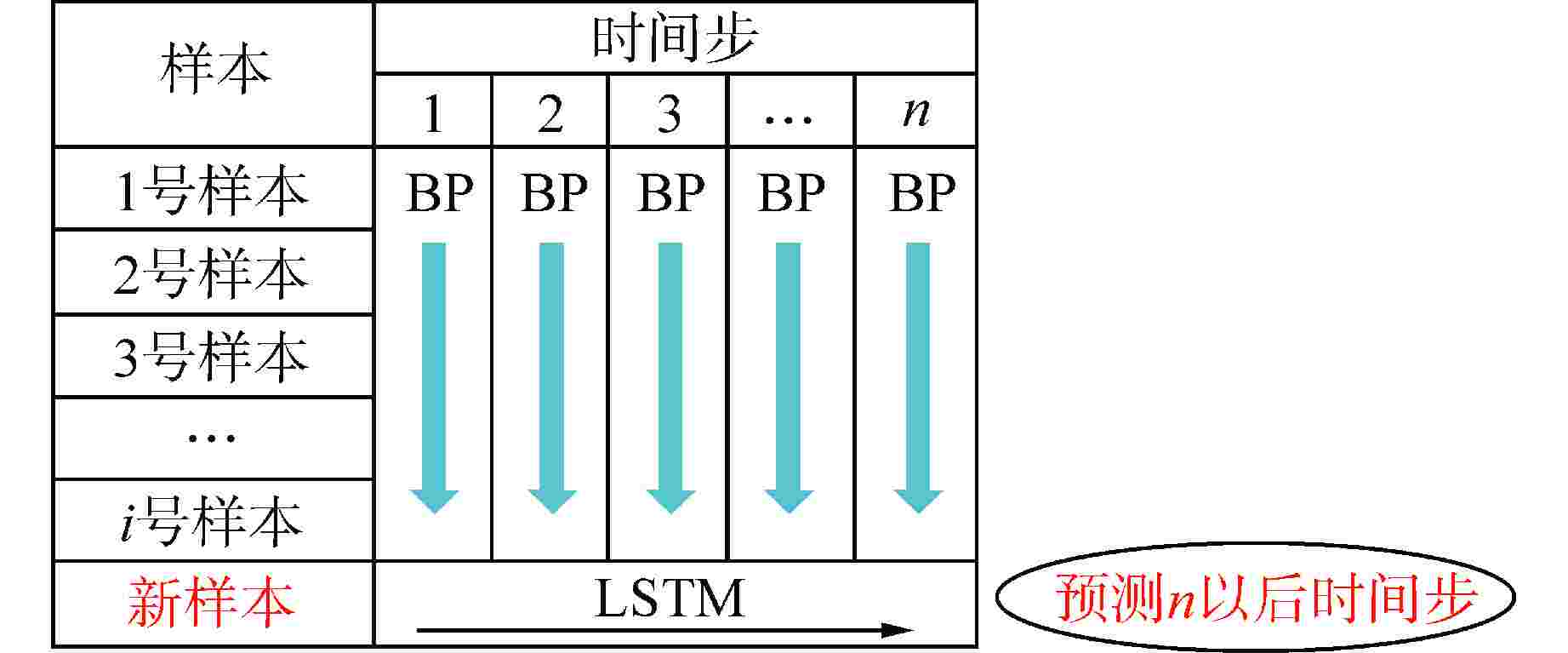
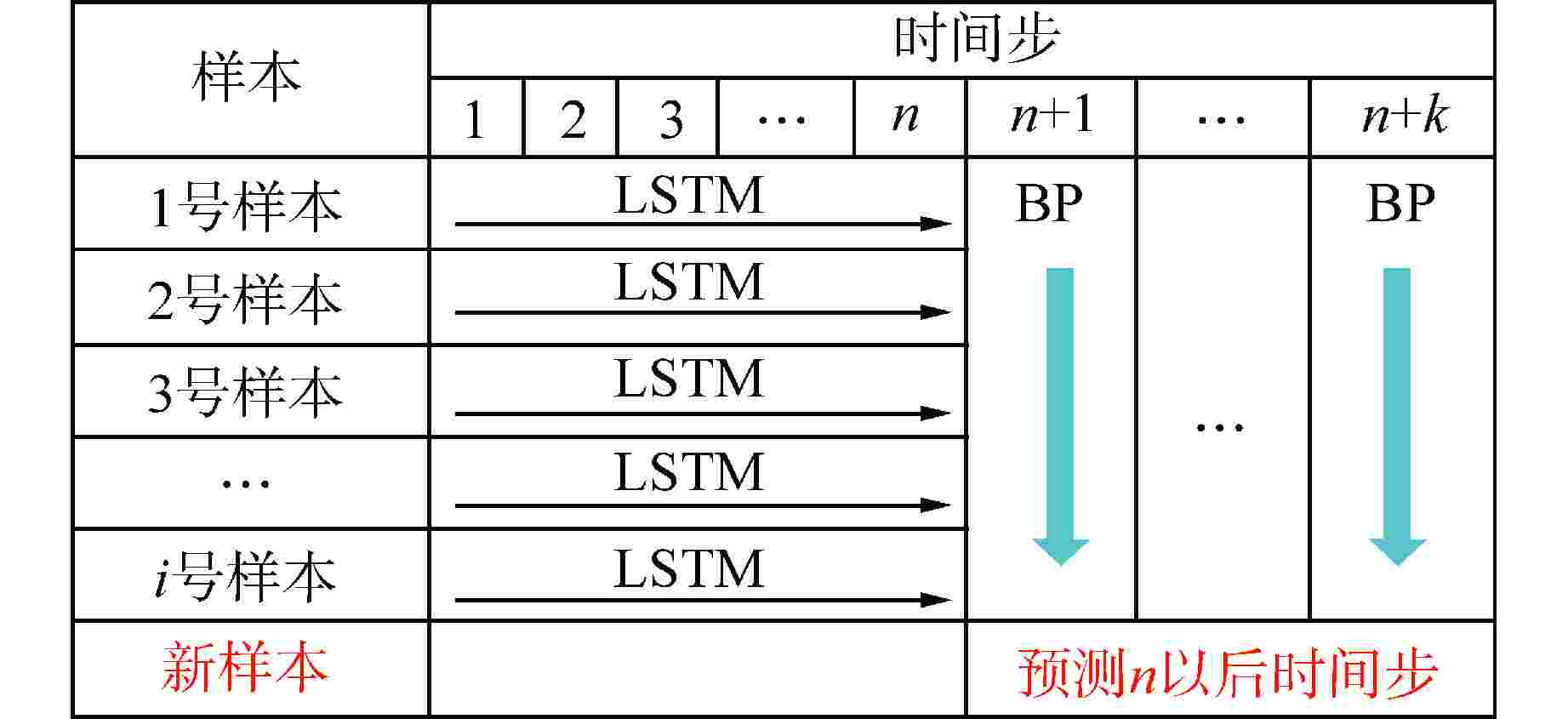
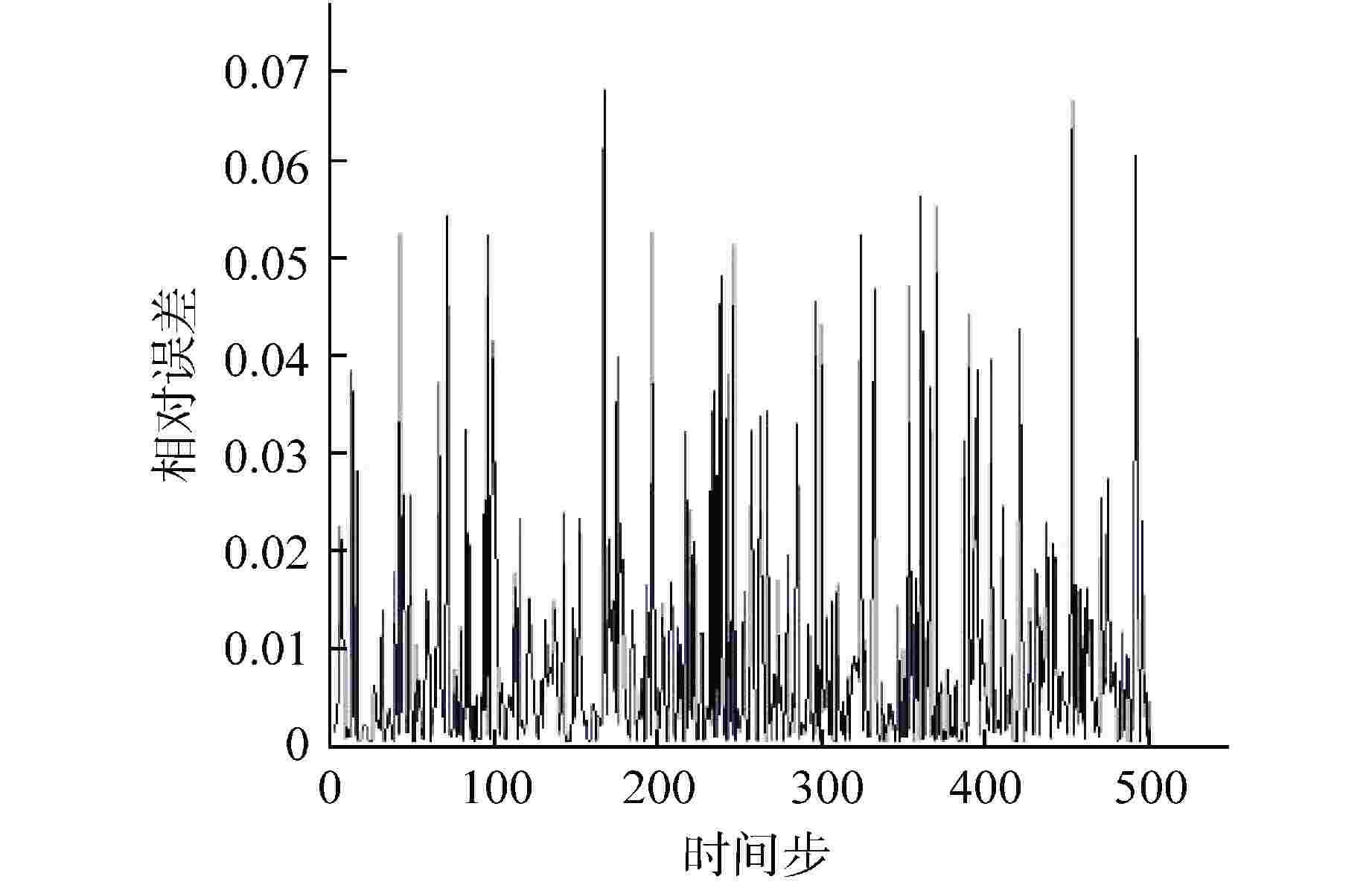
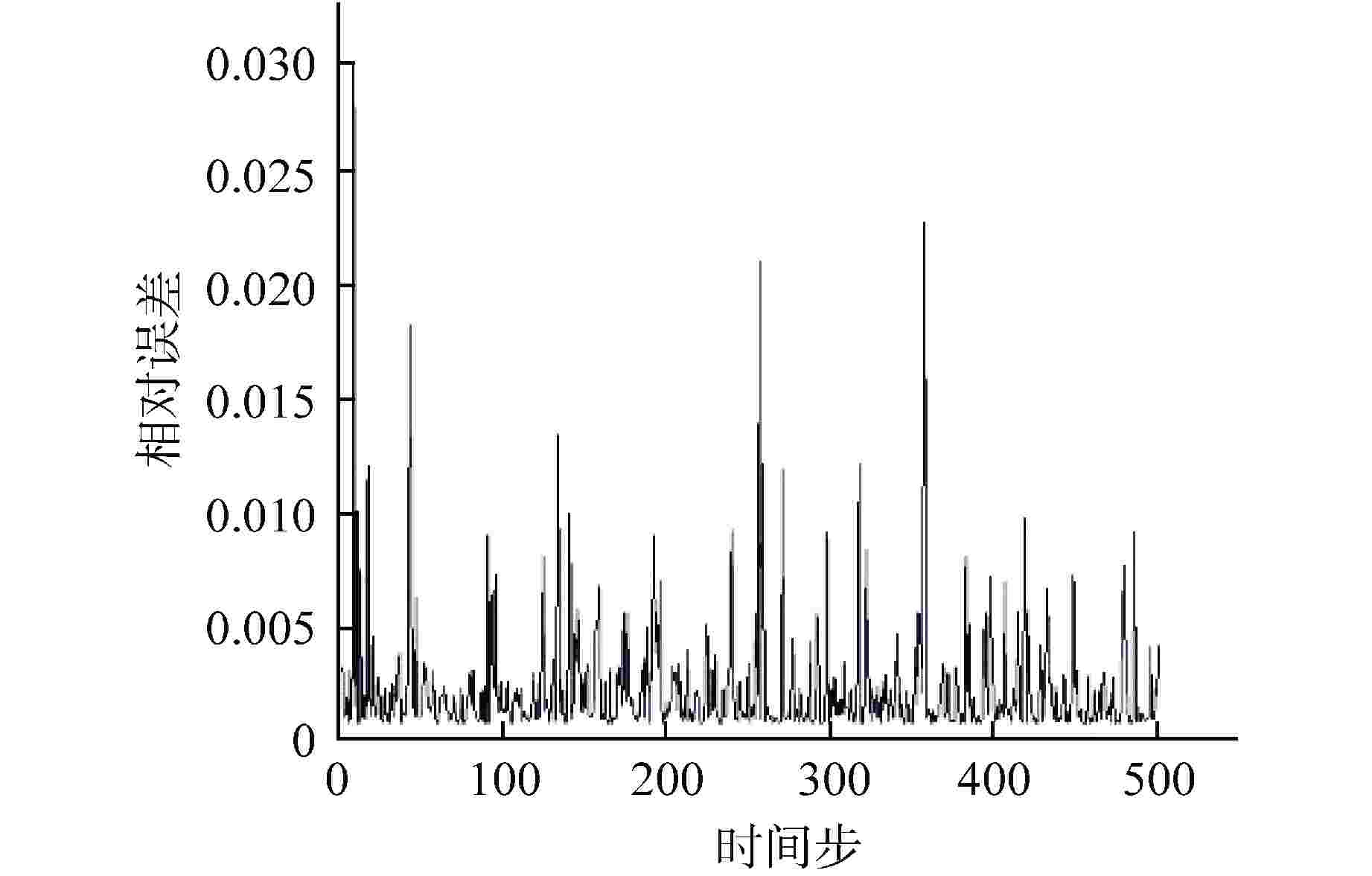
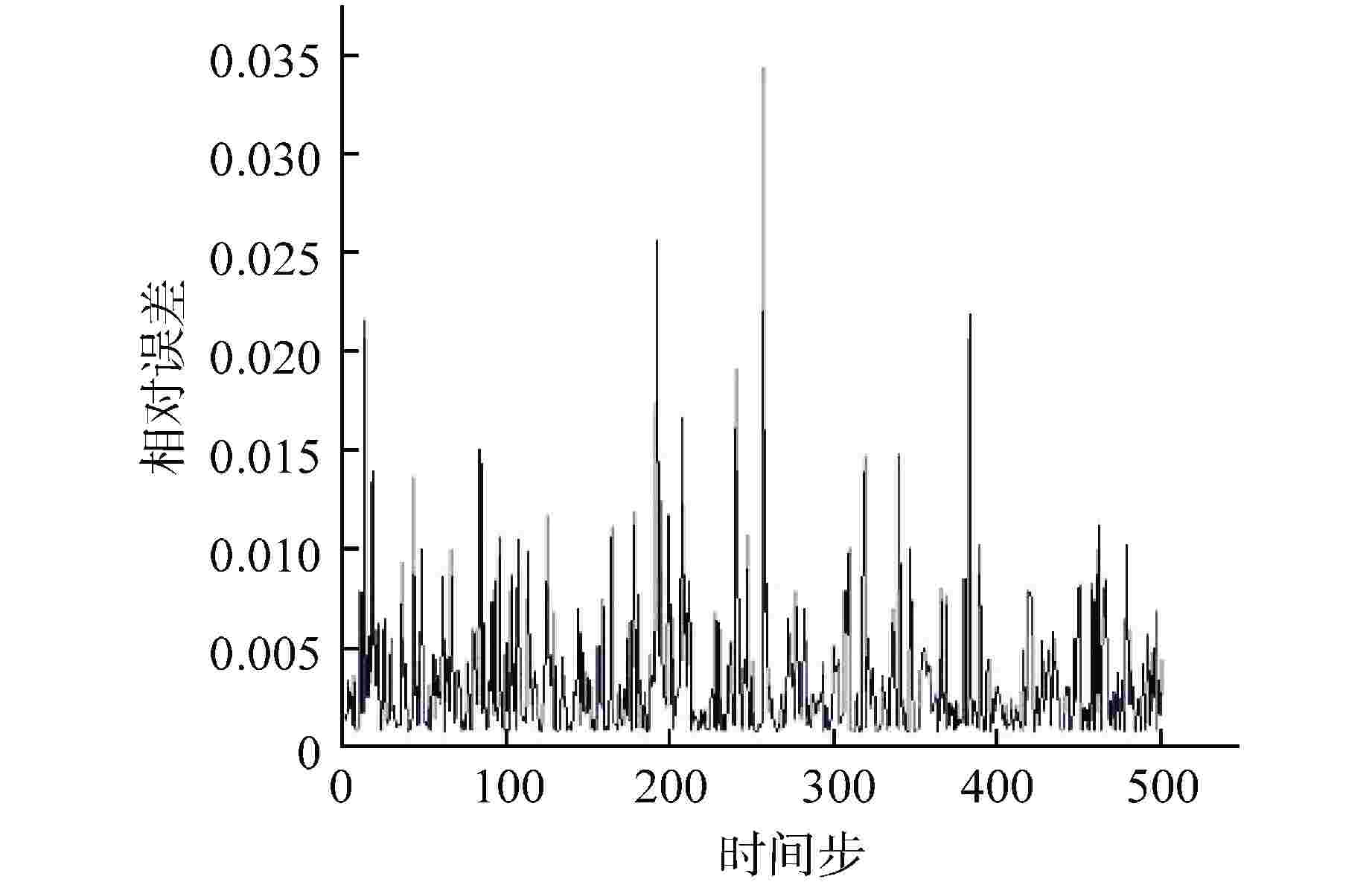
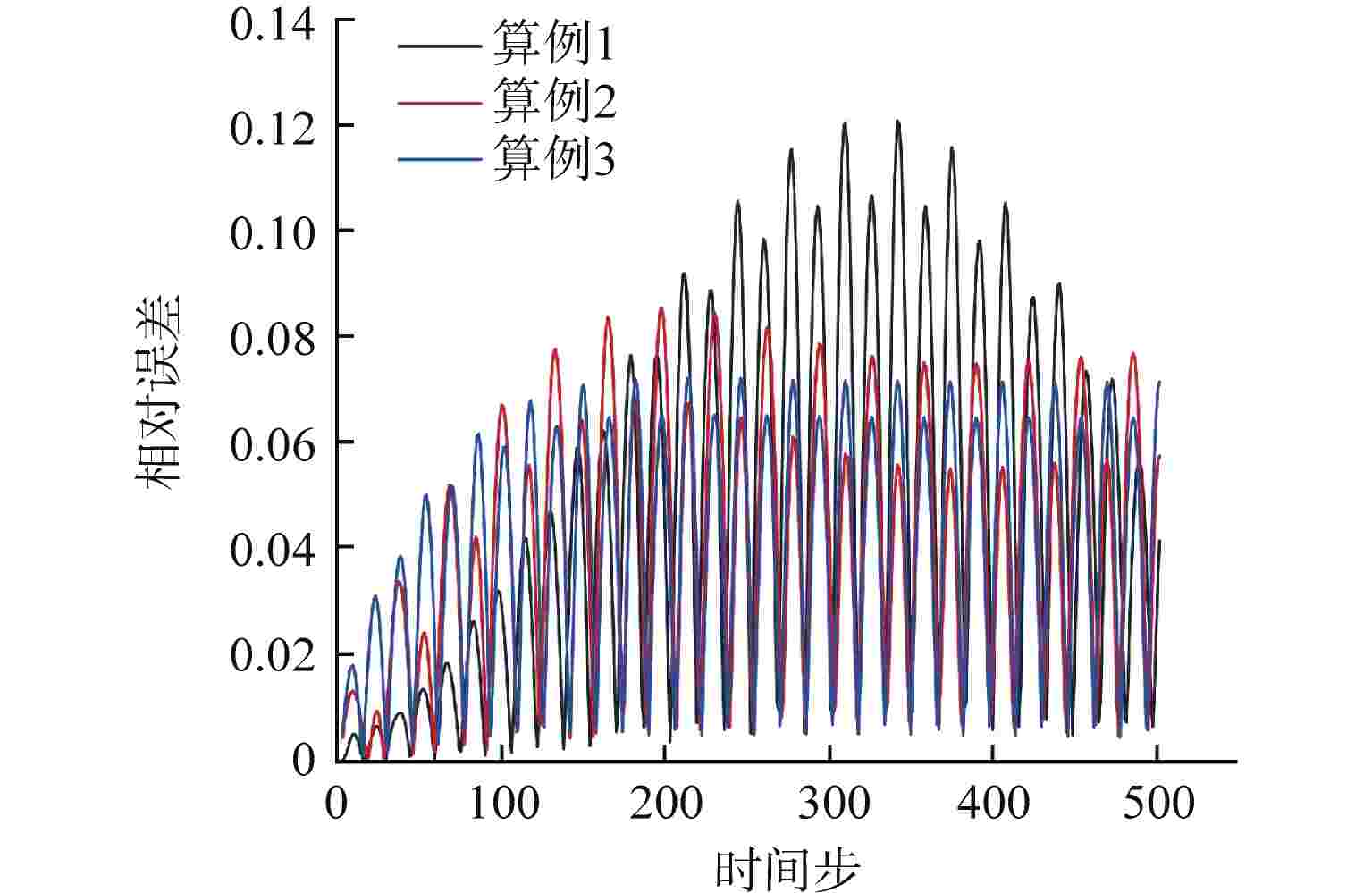
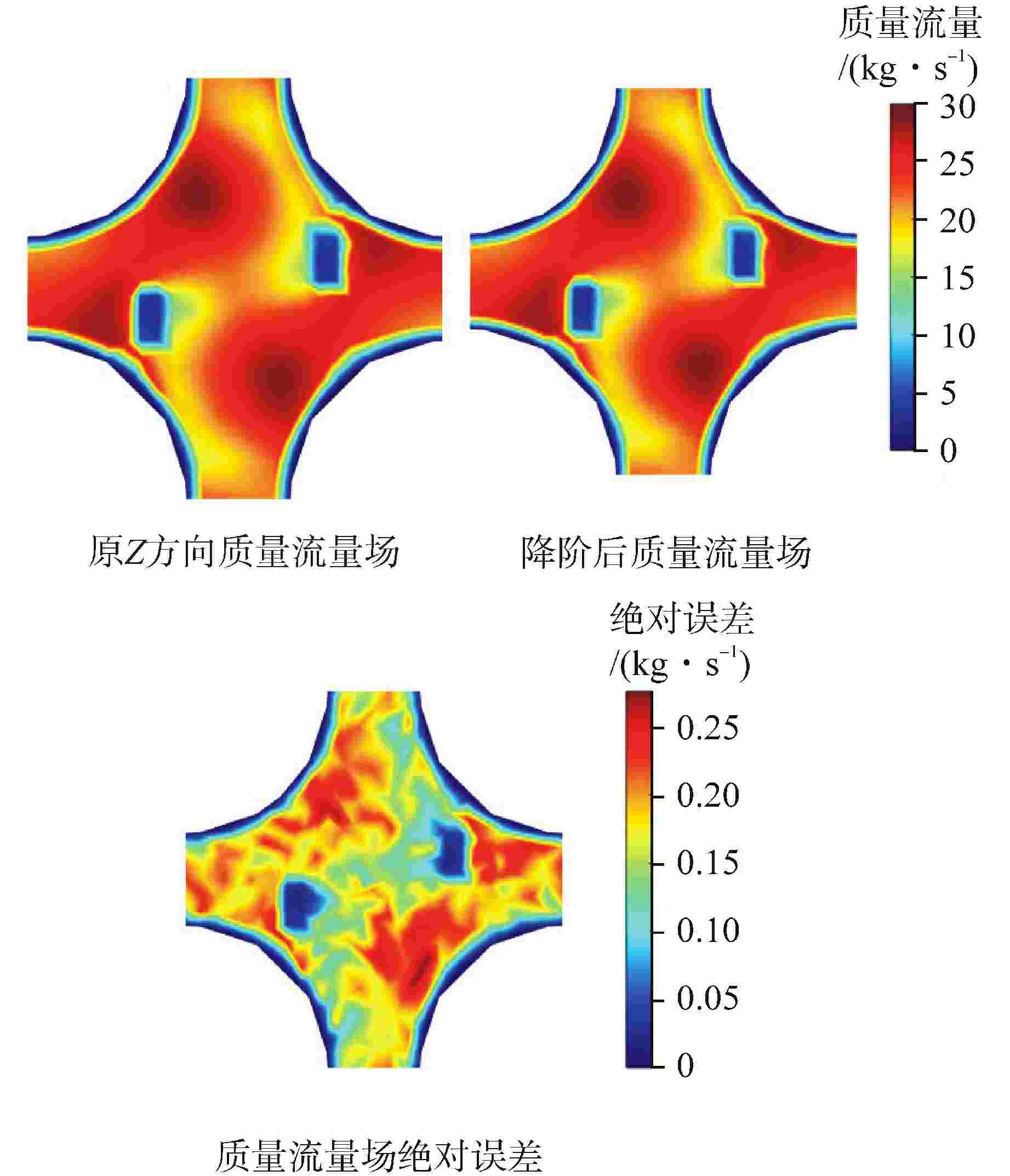
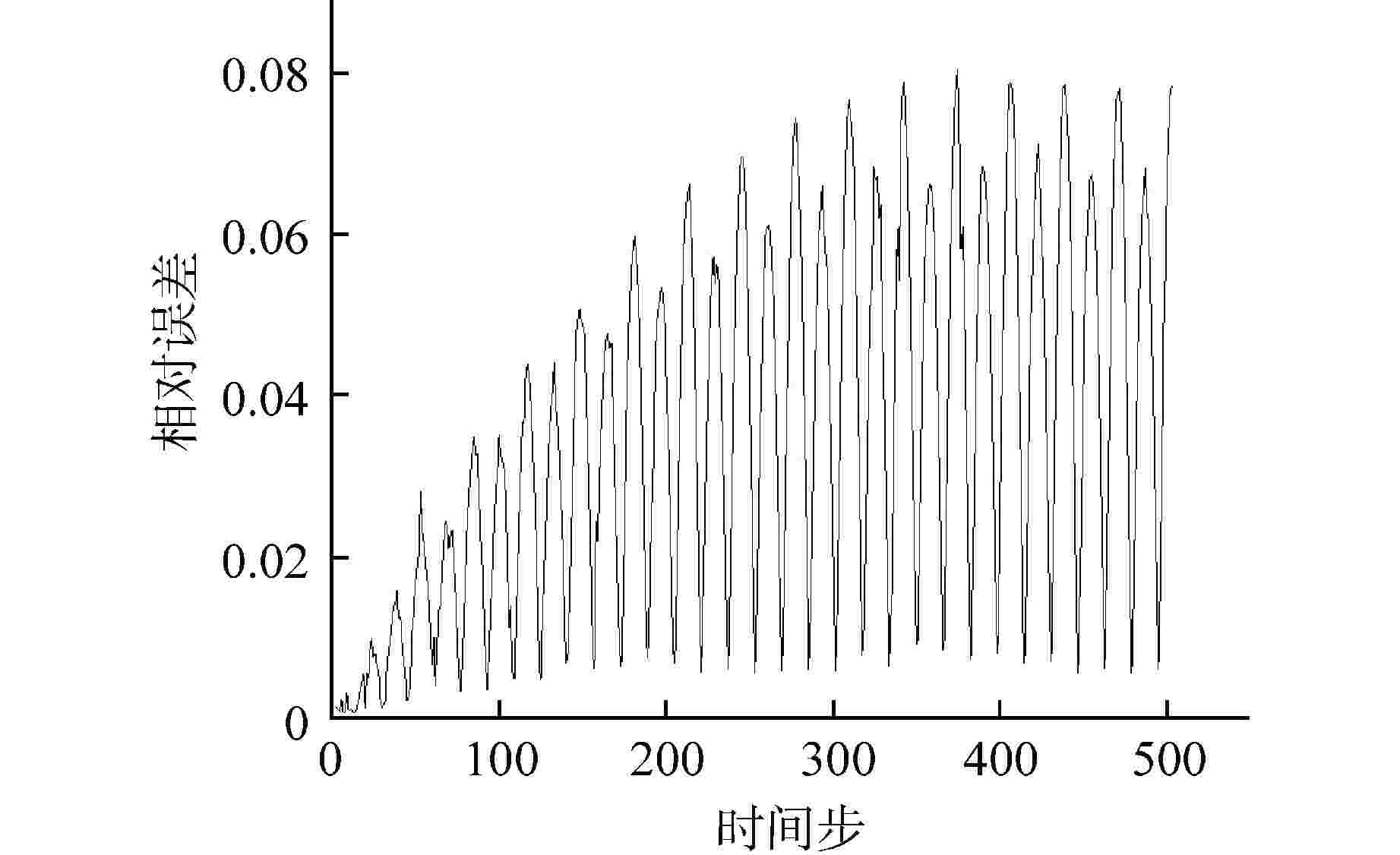
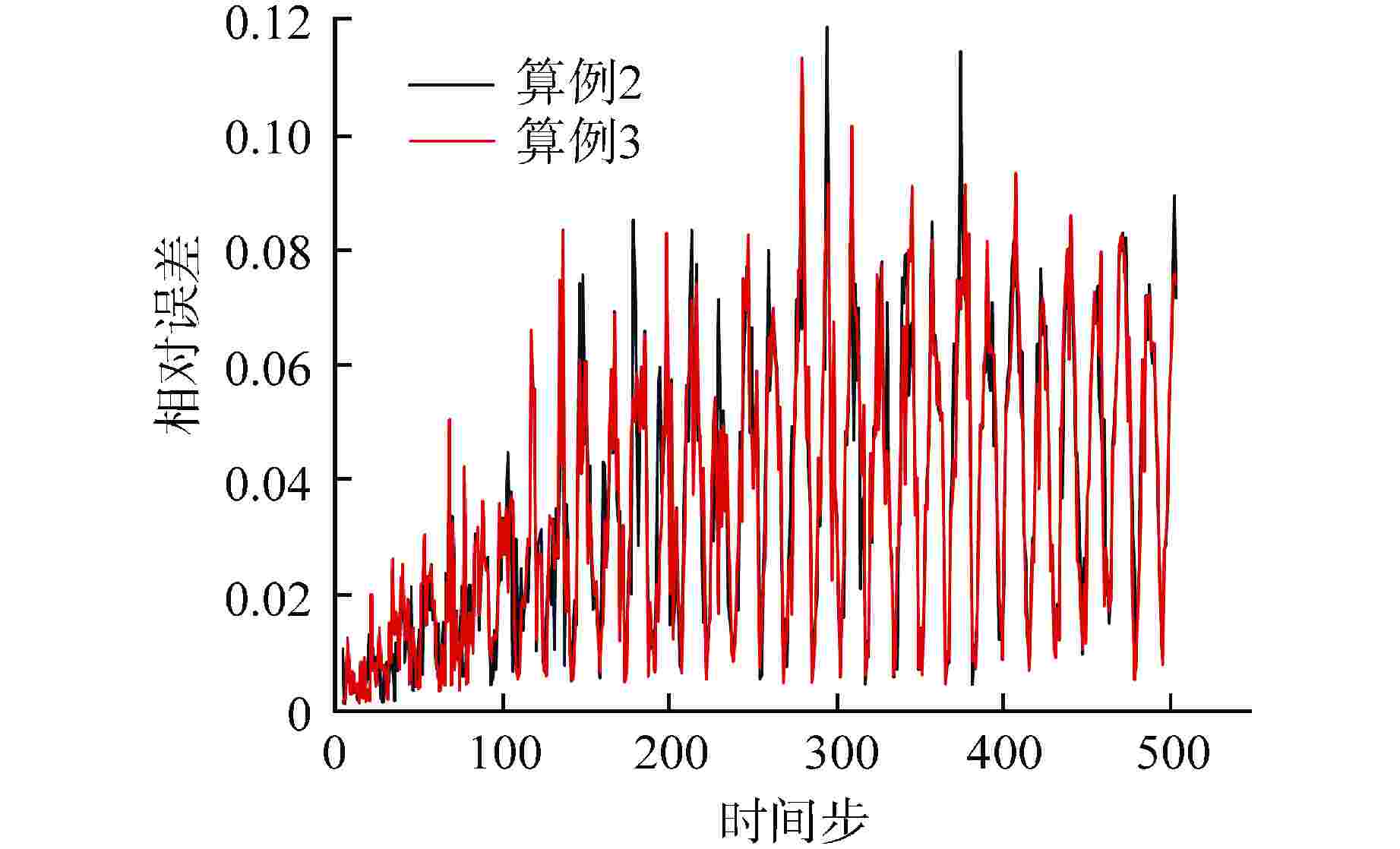
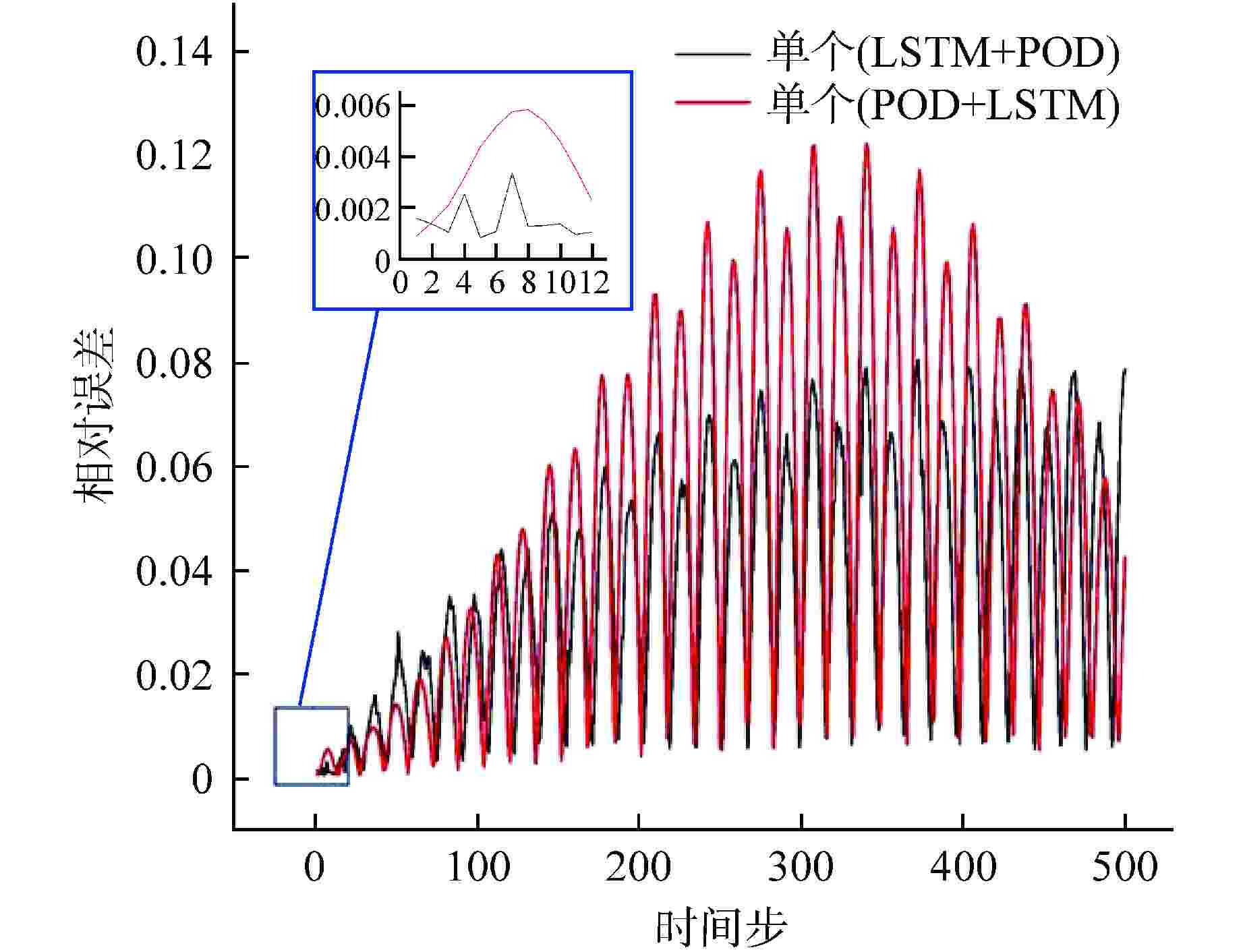
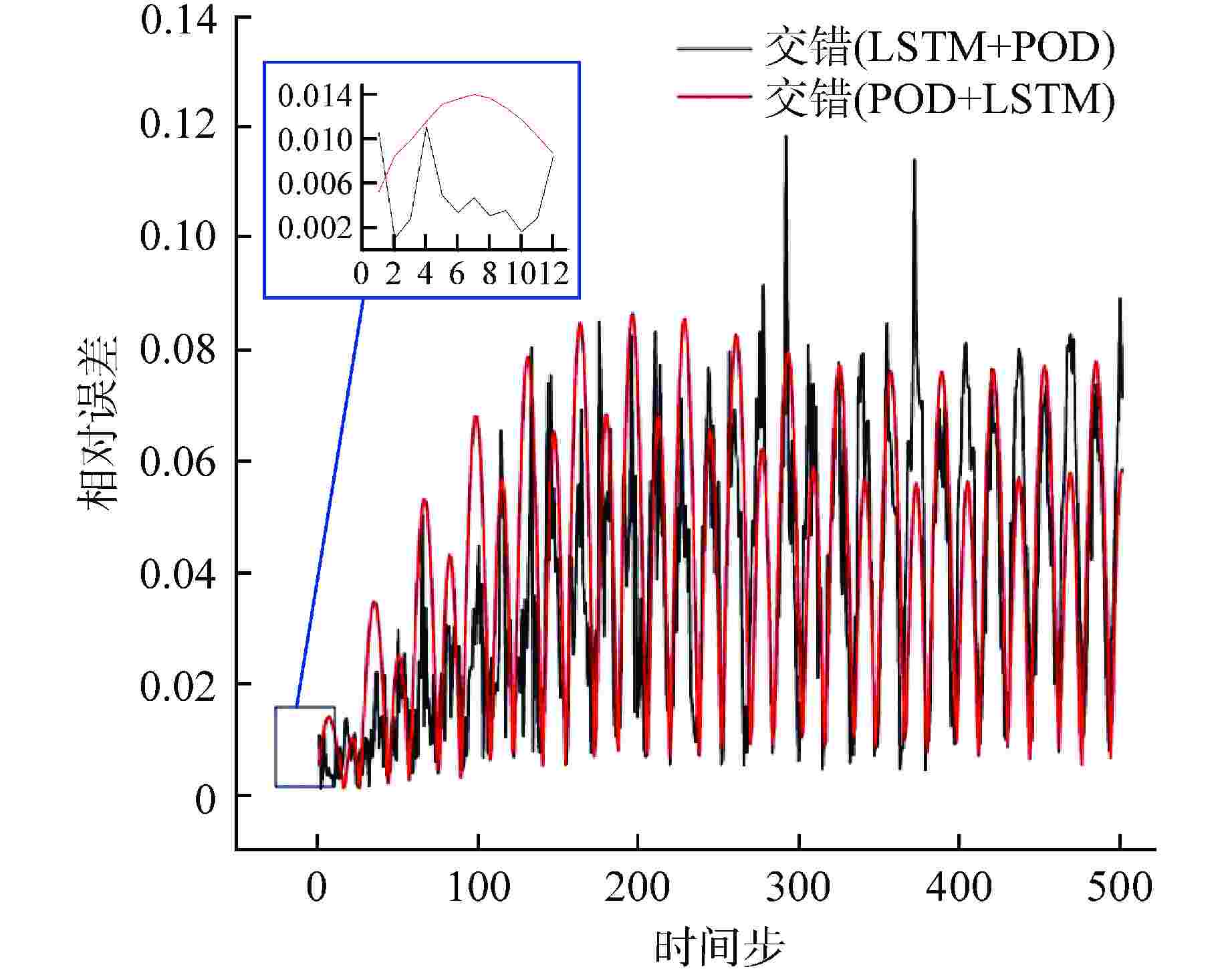
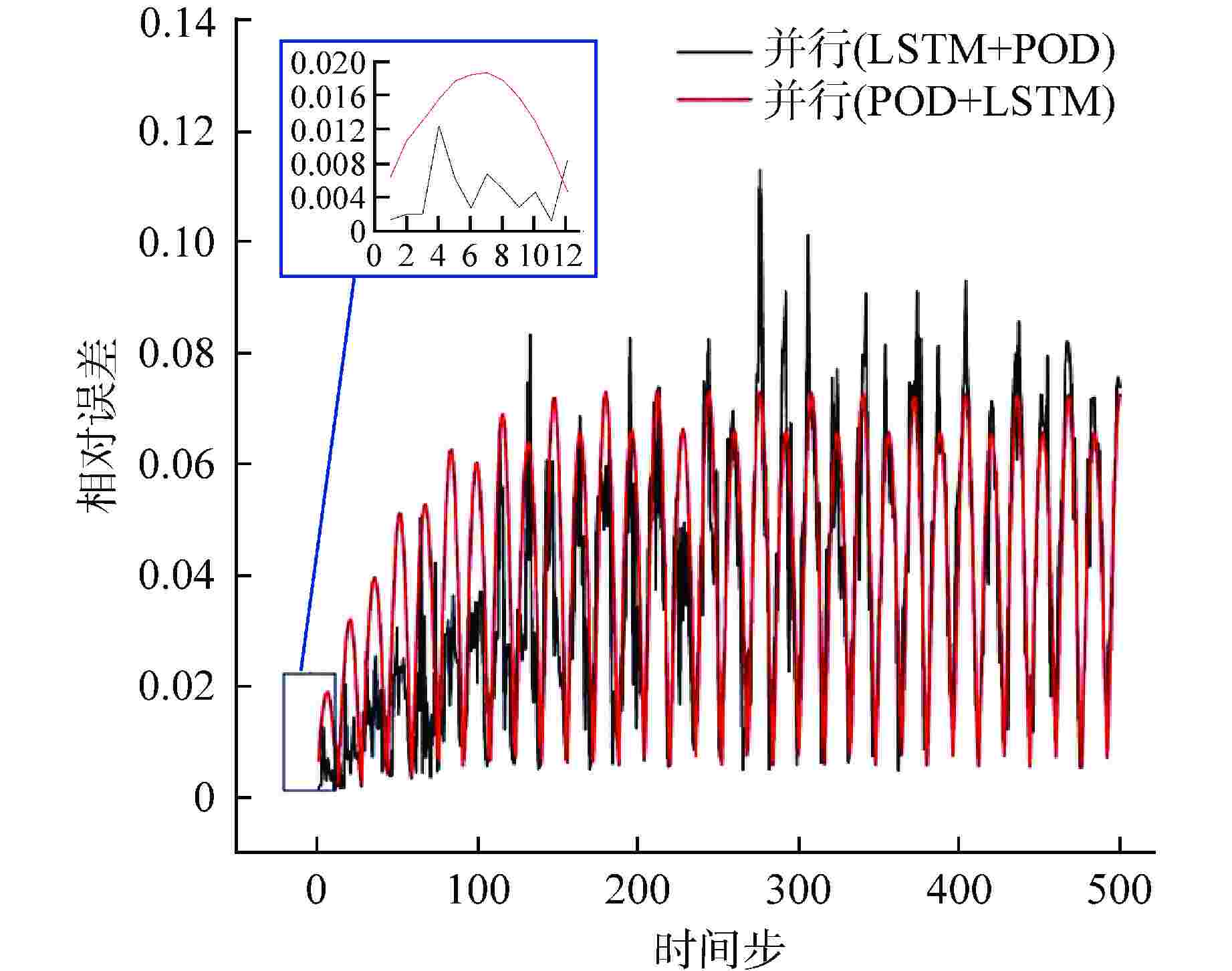
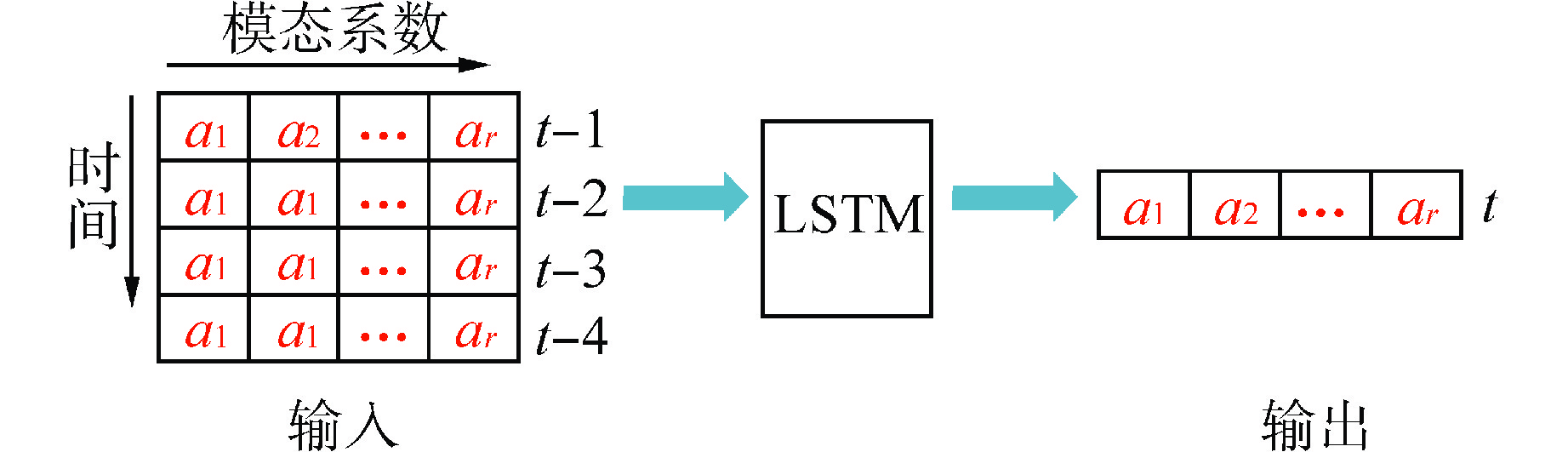
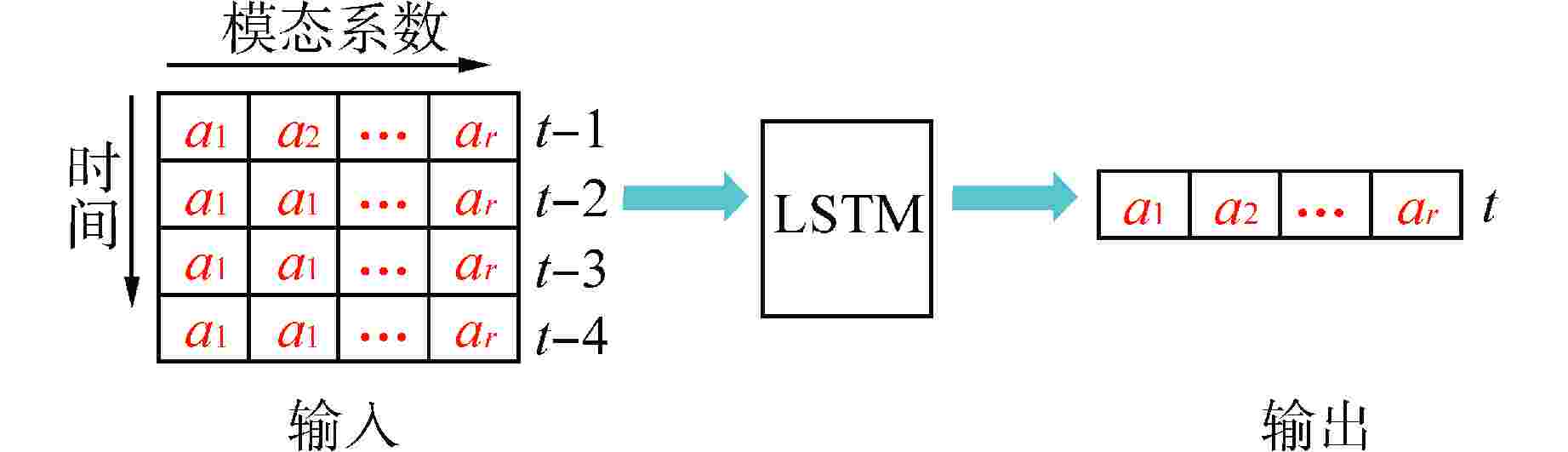
摘要: 降阶模型（ROM）通过将全阶守恒方程映射至低阶子空间或构建数据驱动的代理模型，有效降低了物理模型的复杂性。相比传统的计算流体动力学（CFD）仿真，ROM在大规模仿真计算中计算效率更高。本文利用本征正交分解（POD）结合机器学习（ML），提出了一种适用于瞬态工况的ROM框架，并以此实现棒束子通道内质量流量参数瞬态预测。针对POD和ML不同方式结合的预测方法进行对比，结果显示长短期记忆神经网络（LSTM）+POD方法更适合短期预测，而在长期预测时POD+LSTM方法误差更小，可为未来进行其他复杂系统的预测提供方案。
-
关键词:
- 降阶模型（ROM）技术 /
- 棒束子通道 /
- 机器学习
Abstract: The Reduced Order Model (ROM) effectively reduces the complexity of physical models by mapping full-order conservation equations to lower-order subspaces or building data-driven surrogate models. Compared with traditional computational fluid dynamics (CFD) simulation, ROM is more efficient in large-scale simulation. In this paper, a ROM framework is proposed by combining Proper Orthogonal Decomposition (POD) with machine learning (ML) to predict mass flow parameters in rod bundle subchannels. Comparison of prediction methods for different ways of combining POD and ML shows that the LSTM+POD method is more suitable for short-term prediction, while the POD+LSTM method has less error in long-term prediction, which can provide a solution for making predictions of other complex systems in the future. -
图 5 搅混翼及搅混翼出口流体处网格情况
Figure 5. Mesh Configuration at the Mixing Vane and the Fluid Outlet of Mixing Vane
图 11 POD+LSTM方法算例1、算例2和算例3预测的相对误差
Figure 11. Relative Errors Predicted by POD+LSTM Method for Case 1, Case 2 and Case 3
图 12 算例2在搅混翼出口处预测的第64 s情况
Figure 12. Predicted Condition at 64th Second at the Mixing Vane Outlet for Case 2
图 13 LSTM+POD方法算例1预测的相对误差
Figure 13. Relative Error Predicted by LSTM+POD Method for Case 1
图 14 LSTM+POD方法算例2和算例3预测的相对误差
Figure 14. Relative Errors Predicted by LSTM+POD Method for Case 2 and Case 3
图 15 算例1分别进行两种方法相对误差对比
Figure 15. Comparison of Relative Errors Between Two Methods for Case 1
图 16 算例2分别进行两种方法相对误差对比
Figure 16. Comparison of Relative Errors Between Two Methods for Case 2
图 17 算例3分别进行两种方法相对误差对比
Figure 17. Comparison of Relative Errors Between Two Methods for Case 3
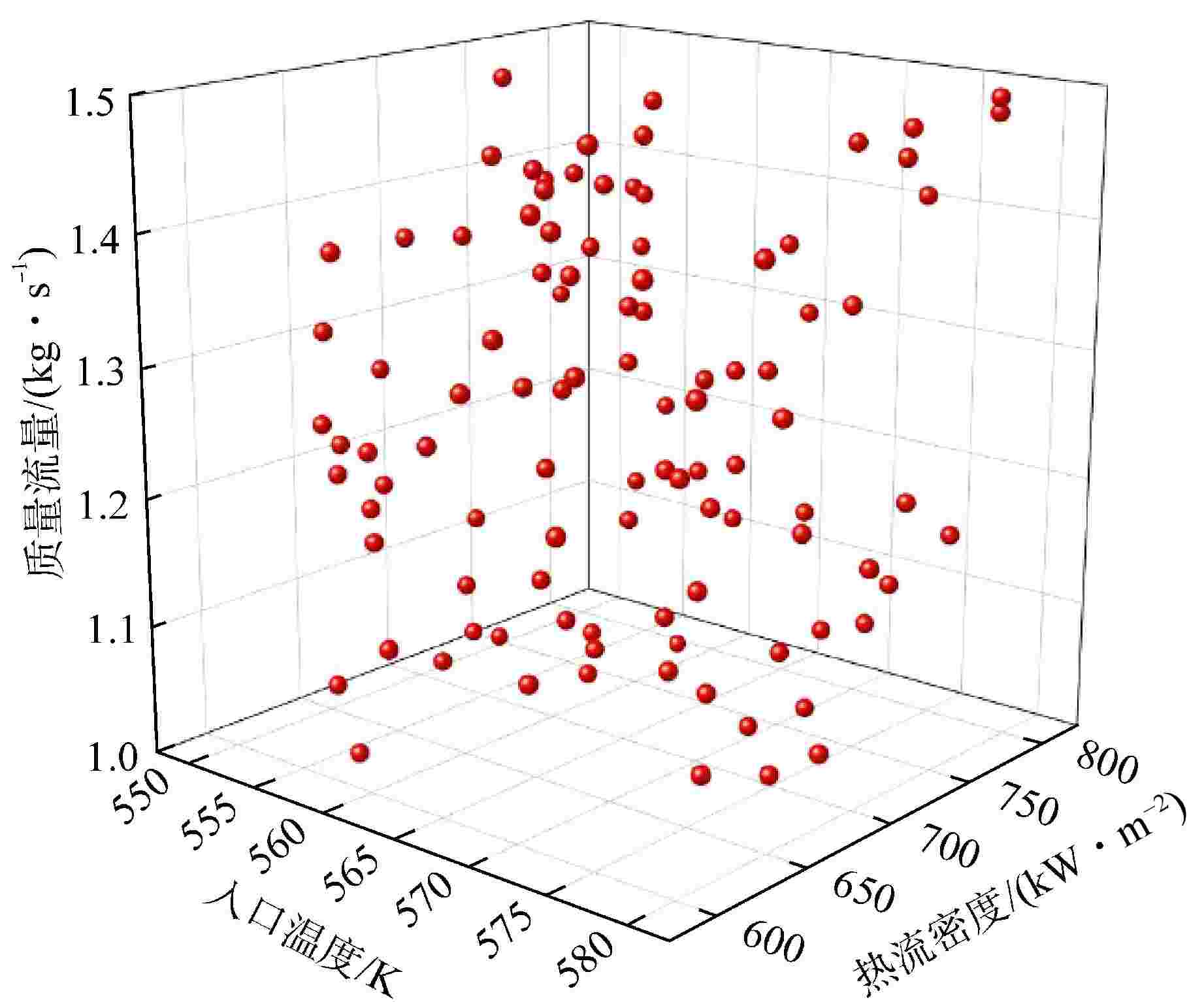
表 1 边界条件参数变化范围
Table 1. Variation Range of Boundary Condition Parameters
参数名 取值范围 入口温度/K （550, 580） 壁面热流密度/(W·m−2) （6×105, 8×105） 入口质量流量/(kg·s−1) （1.0, 1.5） 压力/MPa 14.71 
下载: 导出CSV
-
[1] 高勇,程毅,崔军,等. 基于CFD的绕丝元件棒束通道内流动传热特性研究[J]. 核科学与工程,2024,44(2): 395-403. [2] HE T J, LIU J, YE S J, et al. A novel model order reduction technique for solving horizontal refraction equations in the modeling of three-dimensional underwater acoustic propagation[J]. Journal of Sound and Vibration, 2024, 591: 118617. doi: 10.1016/j.jsv.2024.118617 [3] LUO H, ZHANG X, CUI K E, et al. A multi-scale model-order reduction strategy for vibration analysis of coupled structures with local inhomogeneities[J]. Computers & Structures, 2024, 290: 107191. [4] HE S P, WANG M J, ZHANG J, et al. A deep-learning reduced-order model for thermal hydraulic characteristics rapid estimation of steam generators[J]. International Journal of Heat and Mass Transfer, 2022, 198: 123424. doi: 10.1016/j.ijheatmasstransfer.2022.123424 [5] 温晓,刘琪,高振,等. 局部非侵入式约化基模型在瑞利-泰勒不稳定中的应用[J]. 山东大学学报(理学版),2020,55(2): 109-117. [6] 杨迪,段承杰,丁鹏,等. 参数化流动传热问题的模型降阶方法研究[J]. 原子能科学技术,2024,58(7): 1440-1451. [7] PEARSON K. LIII. On lines and planes of closest fit to systems of points in space[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1901, 2(11): 559-572. doi: 10.1080/14786440109462720 [8] SIROVICH L. Turbulence and the dynamics of coherent structures. I. Coherent structures[J]. Quarterly of Applied Mathematics, 1987, 45(3): 561-571. doi: 10.1090/qam/910462 [9] 王烨,朱欣悦,孙振东. 基于POD降阶模型的正弦波翅片扁管管翅式换热器流动与传热特性分析[J]. 化工学报,2022,73(5): 1986-1994. [10] HAZENBERG M, ASTRID P, WEILAND S. Low order modeling and optimal control design of a heated plate[C]//Proceedings of 2003 European Control Conference. Cambridge: IEEE, 2015: 1240-1245, doi: 10.23919/ECC.2003.7085130. [11] JIANG G H, KANG M, CAI Z W, et al. Data-driven temperature estimation of non-contact solids using deep-learning reduced-order models[J]. International Journal of Heat and Mass Transfer, 2022, 185: 122383. doi: 10.1016/j.ijheatmasstransfer.2021.122383 -
计量
- 文章访问数: 38
- HTML全文浏览量: 14
- PDF下载量: 3
- 被引次数: 0
