Fluid-structure Interaction Dynamic Modeling of Tube Bundle Based on Data-driven
-
摘要: 传热管束是压水堆蒸汽发生器的核心部件，容易发生流致振动问题。在流致振动机理中，漩涡脱落和流弹失稳是典型的强流固耦合问题，无法将结构场与流场解耦求解。为更好地完成蒸汽发生器中管束结构的力学设计，本文通过数据驱动的方式，完成了漩涡脱落和流弹失稳2种流致振动机理的流固耦合动力学建模，并用现有试验数据进行验证，预测结果与试验符合较好。本文方法结合了理论模型的严谨性和计算流体动力学（CFD）计算可考虑实际结构动力学特征的优点，既避免了复杂管束三维流固耦合模拟对海量计算资源的需求，又降低了传统理论模型对于试验数据的依赖，有利于在工程中推广应用。Abstract: The tube bundle is the core component in the pressurized water reactor steam generator, which is prone to flow-induced vibration. In the mechanism of flow-induced vibration, vortex shedding and fluidelastic instability are typical strong fluid-structure interaction problems, which cannot be solved by decoupling the structural field and flow field. In order to better carry out the mechanical design of tube bundle in steam generator, the present work completed the fluid-structure interaction dynamic modeling of two flow-induced vibration mechanisms, vortex shedding and fluidelastic instability, using data-driven method. The prediction results were verified with existing experimental data, and they were in good agreement with the literature results. This method combines the advantages of the theoretical models and the consideration of actual structural dynamics characteristics in CFD calculations. It not only avoids the need for massive computing resources of three-dimensional fluid-structure interaction simulation in complex tube bundle, but also reduces the dependence of traditional theoretical models on experimental data, which is conducive to promoting application in engineering.
-
Key words:
- Data-driven /
- Fluid-structure interaction /
- Tube bundle /
- Dynamic modeling
-
图 1 两端支撑管模型
L—管长度；U—外流流速；D—管外径
Figure 1. Schematic Representation of A Flexible Tube Supported at Both Ends
图 6 管的运动轨迹
η—无量纲横向（升力方向）位移，η=y/D；χ—无量纲流向位移，χ=x/D(x、y—流向、横向位移)
Figure 6. Trajectory of Tube Motion
图 8 基于准稳态模型的动力学建模流程
P/D—管束节径比；Re—雷诺数；Δx、Δy—中心管在x向、y向的位移偏移量；m*—无量纲质量，$ {m^*} = m/\rho {D^2} $；δ—对数衰减率；$ C\mathrm{_{L0}} $、$ C_{\mathrm{D}0} $—升力系数、阻力系数的平均值；CL、CD—升力系数、阻力系数；F—流体力；Ucr—临界流速
Figure 8. Dynamic Modeling Process Based on Quasi-steady Model
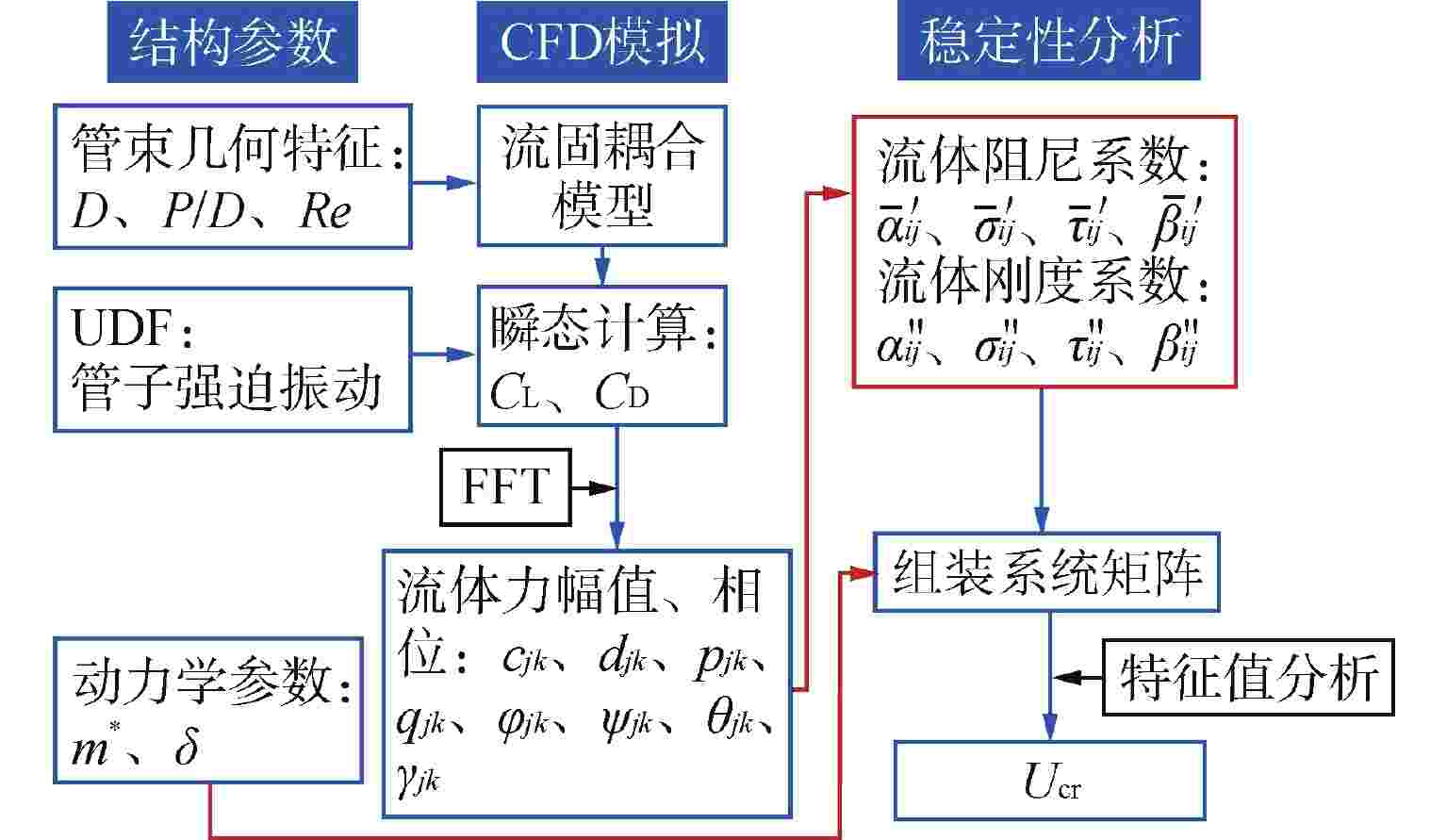
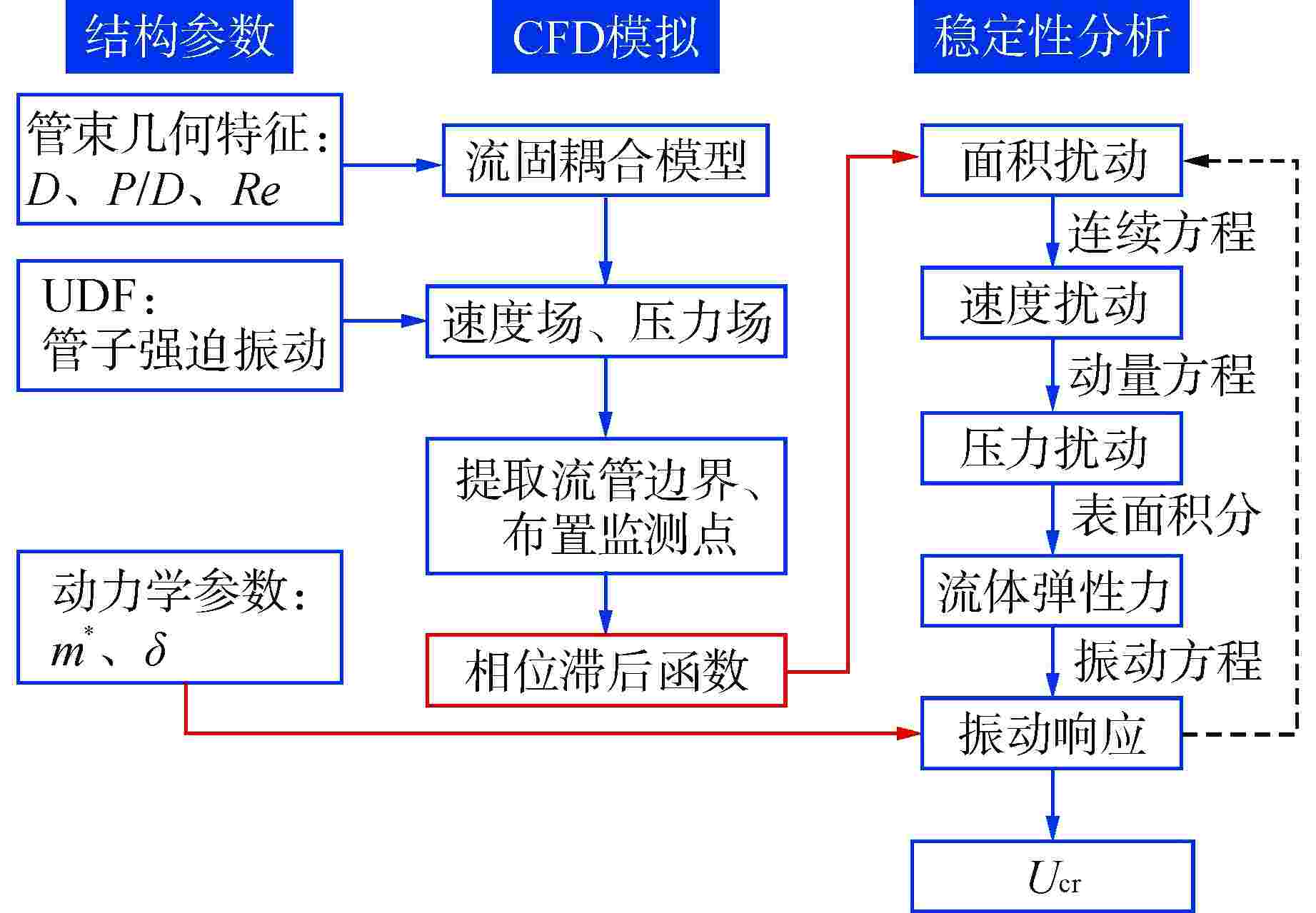
图 9 基于非稳态模型的动力学建模流程
$ c_{jk} $、$ d_{j k} $、$ p_{j k} $、$ q_{j k} $—流体力系数的幅值；$ \varphi_{jk} $、$ \psi_{j k} $、$ \theta_{jk} $、$ \gamma_{f k} $—流体力与位移间的相位角；$ {\bar \alpha _{ij}}^\prime $、$ {\bar \sigma _{ij}}^\prime $、$ {\bar \tau _{ij}}^\prime $、$ {\bar \beta _{ij}}^\prime $—流体阻尼系数；$ {\alpha ''_{ij}} $、$ {\sigma ''_{ij}} $、$ {\tau ''_{ij}} $、$ {\beta ''_{ij}} $—流体刚度系数；UDF—用户自定义函数；FFT—快速傅里叶变换
Figure 9. Dynamic Modeling Process Based on Unsteady Model
-
[1] 姜乃斌,冯志鹏,臧峰刚,等. 核工程中的流致振动理论与应用[M]. 上海: 上海交通大学出版社,2018: 3-203. [2] GABBAI R D, BENAROYA H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J]. Journal of Sound and Vibration, 2005, 282(3-5): 575-616. doi: 10.1016/j.jsv.2004.04.017 [3] FENG Z P, ZANG F G, QI H H, et al. Modeling of vortex-induced vibrations for a flexible tube subjected to both internal fluid flow and external cross-flow[J]. Annals of Nuclear Energy, 2022, 175: 109203. doi: 10.1016/j.anucene.2022.109203 [4] 冯志鹏,张毅雄,臧峰刚,等. 三维弹性管的涡致振动特性分析[J]. 应用数学和力学,2013, 34(9): 976-985. doi: 10.3879/j.issn.1000-0887.2013.09.011 [5] PRICE S J. A review of theoretical models for fluidelastic instability of cylinder arrays in cross-flow[J]. Journal of Fluids and Structures, 1995, 9(5): 463-518. doi: 10.1006/jfls.1995.1028 [6] 冯志鹏,蔡逢春,臧峰刚,等. 管束结构流弹失稳的数值预测方法研究[J]. 振动与冲击,2023, 42(23): 49-54. [7] AUSTERMANN R, POPP K. Stability behaviour of a single flexible cylinder in rigid tube arrays of different geometry subjected to cross-flow[J]. Journal of Fluids and Structures, 1995, 9(3): 303-322. doi: 10.1006/jfls.1995.1017 [8] MAHON J, MESKELL C. Surface pressure survey in a parallel triangular tube array[J]. Journal of Fluids and Structures, 2012, 34: 123-137. doi: 10.1016/j.jfluidstructs.2012.05.005 [9] PRICE S J, ZAHN M L. Fluidelastic behaviour of a normal triangular array subject to cross-flow[J]. Journal of Fluids and Structures, 1991, 5(3): 259-278. doi: 10.1016/0889-9746(91)90485-8 [10] CHEN S S. Instability mechanisms and stability criteria of a group of circular cylinders subjected to cross-flow-Part 2: numerical results and discussions[J]. Journal of Vibration and Acoustics, 1983, 105(2): 253-260. doi: 10.1115/1.3269095 [11] WEAVER D S, El-KASHLAN M. The effect of damping and mass ratio on the stability of a tube bank[J]. Journal of Sound and Vibration, 1981, 76(2): 283-294. doi: 10.1016/0022-460X(81)90355-2 -
下载:
计量
- 文章访问数: 71
- HTML全文浏览量: 13
- PDF下载量: 16
- 被引次数: 0
