Development and Application of a Mechanical Model for Multilayer Anisotropic Cladding
-
摘要: 由高致密度纯SiC和SiC纤维/基体复合材料(SiCf/SiC)组成的多层SiC复合包壳是当前事故容错燃料(ATF)包壳的热门选型,当前应用的典型燃料性能分析程序缺乏对于SiCf/SiC材料各向异性力学行为的建模能力,为提高燃料性能分析中复合SiC包壳力学计算的准确性,本文开发了一套适用于多层各向异性材料的力学模型,并将其集成到燃料性能分析程序FRAPCON4.0中,采用多层SiC包壳热力耦合算例对模型正确性进行了验证。实现了对具有正交各向异性力学特性和多轴类塑性行为的SiC复合包壳的力学计算功能,分析了双层SiC包壳燃料元件堆内稳态运行工况的性能。本研究建立的力学模型适用于任意多层圆柱结构燃料元件,并具备正交各向异性力学参数及行为的分析能力,可应用于多种新型燃料元件分析。
-
关键词:
- SiC包壳 /
- 事故容错燃料(ATF) /
- 芯块-包壳机械相互作用(PCMI) /
- 各向异性材料
Abstract: The multilayer SiC composites cladding composed of monolithic SiC and SiC fiber/matrix composite (SiCf/SiC) is a popular choice for accident-tolerant fuel cladding. However, typical fuel performance analysis codes currently lack the modeling capability for the anisotropic mechanical behavior of SiCf/SiC materials. In order to enhance the precision of mechanical calculations for composite SiC cladding in fuel performance analysis, a mechanical model was developed for multilayer anisotropic materials and integrated into the fuel performance analysis code FRAPCON4.0. Validation of the model's accuracy was conducted using a multilayer SiC cladding thermal-mechanical coupling case. The mechanical calculation capability for SiC composite cladding with orthotropic mechanical properties and multiaxial pseudoplastic behavior was achieved, and the performance of duplex-layer SiC cladding fuel elements under normal operation condition was analyzed. The developed mechanical model in this study is adaptable to arbitrary multilayer cylindrical structure fuel elements and has the capability to analyze orthotropic mechanical parameters and behaviors, rendering it applicable to various types of novel fuel element analyses. -
0. 引 言
日本福岛核事故后,事故容错燃料(ATF)成为研究热点,研究人员进行了大量的理论和实验研究,并提出了多种ATF包壳选型[1]。其中,碳化硅(SiC)包壳由于其良好的中子经济性、高温下机械强度、耐腐蚀能力等优势,成为当前ATF包壳材料的热门选型[2-4]。当前有2种典型的用于核燃料包壳的SiC材料,分别是通过化学气相沉积(CVD)制备的高致密度纯SiC(mSiC)[5]和通过化学气相渗透方法[6]制备的SiC纤维增强陶瓷基复合材料(CMC)SiCf/SiC。由于CVD型SiC天然的高脆性,在压水堆(PWR)运行条件下难以保持完整性。CMC型SiC具有高孔隙率,不能确保包壳材料的气密性,但具有较强的抗拉性能。相关研究分析了单CVD、单CMC和多层SiC复合包壳的力学性能,提出了双层CMC/CVD和3层CVD/CMC/EBC(EBC表示环境障涂层)等多层SiC包壳设计[7]。
目前国内外已有许多研究计算并分析了不同结构SiC包壳的热力行为和失效概率等。Ben-Belgacem等[8]建立了二维SiC/SiC包壳分析程序,并对SiC/SiC辐照的应力和应变分布进行了初步计算。Lee等[3]建立了多层SiC包壳热力行为及失效模型,对双层和三层SiC设计进行了分析和比较。Deng等[9]添加了基于FRAPCON4.0的多层SiC包壳模型,以实现SiC复合包壳燃料的稳态性能分析。Hyuntaek Rho等[10]开发了一个用于稳态和大破口失水事故(LBLOCA)分析的二维轴对称SiC包壳力学模型,分析了多轴类塑性对失效的影响。当前针对SiC包壳的力学性能分析大多采用各向同性假设,部分考虑了各向异性物性的分析仅针对单独CMC型SiC包壳。当前工程中应用的典型燃料性能分析程序不具备计算多层各向异性包壳力学行为的能力。
鉴于此,本文自主开发了一个考虑各向异性材料特性的1.5维轴对称力学模型,并将其集成到燃料性能分析程序FRAPCON4.0中。所建立的力学模型通过有限差分法求解,可用于分析单层正交各向异性材料、多层各向异性包壳的层间以及芯块-包壳之间机械相互作用(PCMI)。比较了SiC复合包壳和Zr-4包壳在正常运行工况下的性能。分析了多层各向异性材料模型在先进燃料建模和分析中的潜在应用。
1. 多层各向异性包壳力学模型
1.1 单层各向异性包壳建模
对于各向同性材料,应力和应变之间的关系可以用轴对称坐标下的广义胡克定律来描述:
$$ \left\{ {\begin{array}{*{20}{c}} {{\varepsilon _r} = \dfrac{1}{E}[{\sigma _r} - v({\sigma _\theta } + {\sigma _{\textit{z}}})] + \varepsilon _r^{^{{\prime}}}} \\ {{\varepsilon _\theta } = \dfrac{1}{E}[{\sigma _\theta } - v({\sigma _r} + {\sigma _{\textit{z}}})] + \varepsilon _\theta ^{^{{\prime}}}} \\ {{\varepsilon _{\textit{z}}} = \dfrac{1}{E}[{\sigma _{\textit{z}}} - v({\sigma _\theta } + {\sigma _r})] + \varepsilon _{\textit{z}}^{^{{\prime}}}} \end{array}} \right. $$ (1) 式中,ε为应变;E 为杨氏模量,Pa;ν为泊松比;σ为应力,Pa;${\varepsilon ^{^{{\prime}}}}$为其他本征应变项(热膨胀、辐照肿胀等)及塑性应变项之和;下标r、θ、z分别为径向、环向、轴向。
对于CMC型SiC,由于其微观纤维编织方式,表现出正交各向异性的力学特性。对于正交各向异性材料,其应力-应变关系可以用以下本构方程描述:
$$ \left[ \begin{gathered} {\varepsilon _r} \\ {\varepsilon _\theta } \\ {\varepsilon _{\textit{z}}} \\ {\gamma _{\theta {\textit{z}}}} \\ {\gamma _{r{\textit{z}}}} \\ {\gamma _{r\theta }} \\ \end{gathered} \right] = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{E_r}}}}&{\dfrac{{ - {\nu _{\theta r}}}}{{{E_\theta }}}}&{\dfrac{{ - {\nu _{{\textit{z}}r}}}}{{{E_{\textit{z}}}}}}&0&0&0 \\ {\dfrac{{ - {\nu _{r\theta }}}}{{{E_r}}}}&{\dfrac{1}{{{E_\theta }}}}&{\dfrac{{ - {\nu _{{\textit{z}}\theta }}}}{{{E_{\textit{z}}}}}}&0&0&0 \\ {\dfrac{{ - {\nu _{r{\textit{z}}}}}}{{{E_r}}}}&{\dfrac{{ - {\nu _{\theta {\textit{z}}}}}}{{{E_\theta }}}}&{\dfrac{1}{{{E_{\textit{z}}}}}}&0&0&0 \\ 0&0&0&{\dfrac{1}{{{G_{\theta {\textit{z}}}}}}}&0&0 \\ 0&0&0&0&{\dfrac{1}{{{G_{r{\textit{z}}}}}}}&0 \\ 0&0&0&0&0&{\dfrac{1}{{{G_{r\theta }}}}} \end{array}} \right]\left[ \begin{gathered} {\sigma _r} \\ {\sigma _\theta } \\ {\sigma _{\textit{z}}} \\ {\tau _{\theta {\textit{z}}}} \\ {\tau _{r{\textit{z}}}} \\ {\tau _{r\theta }} \\ \end{gathered} \right] $$ (2) 式中,G为剪切模量,Pa;γ为切应变;τ为剪切应力,Pa。
根据对称性有:
$$ \dfrac{\nu_{ij}}{E_i}=\dfrac{\nu_{ji}}{E_j}\qquad\left(i,j=r,\ \theta,\ z\right) $$ (3) 由于燃料棒的轴向尺寸远大于其他2个方向,因此可以将其简化为具有均匀轴向应变的广义平面应变问题,并忽略切应变和切应力。柱坐标下的平衡方程为:
$$ \left\{ \begin{gathered} \dfrac{{{\text{d}}{\sigma _r}}}{{{\text{d}}r}} + \dfrac{{{\sigma _r} - {\sigma _\theta }}}{r} = 0 \\ \dfrac{{{\text{d}}{\varepsilon _\theta }}}{{{\text{d}}r}} + \dfrac{{{\varepsilon _\theta } - {\varepsilon _r}}}{r} = 0 \\ \dfrac{{{\text{d}}{\varepsilon _{\textit{z}}}}}{{{\text{d}}r}} = 0 \\ \end{gathered} \right. $$ (4) 将正交各向异性材料的本构关系带入式(4),可以得到与各向异性物性相关的平衡方程:
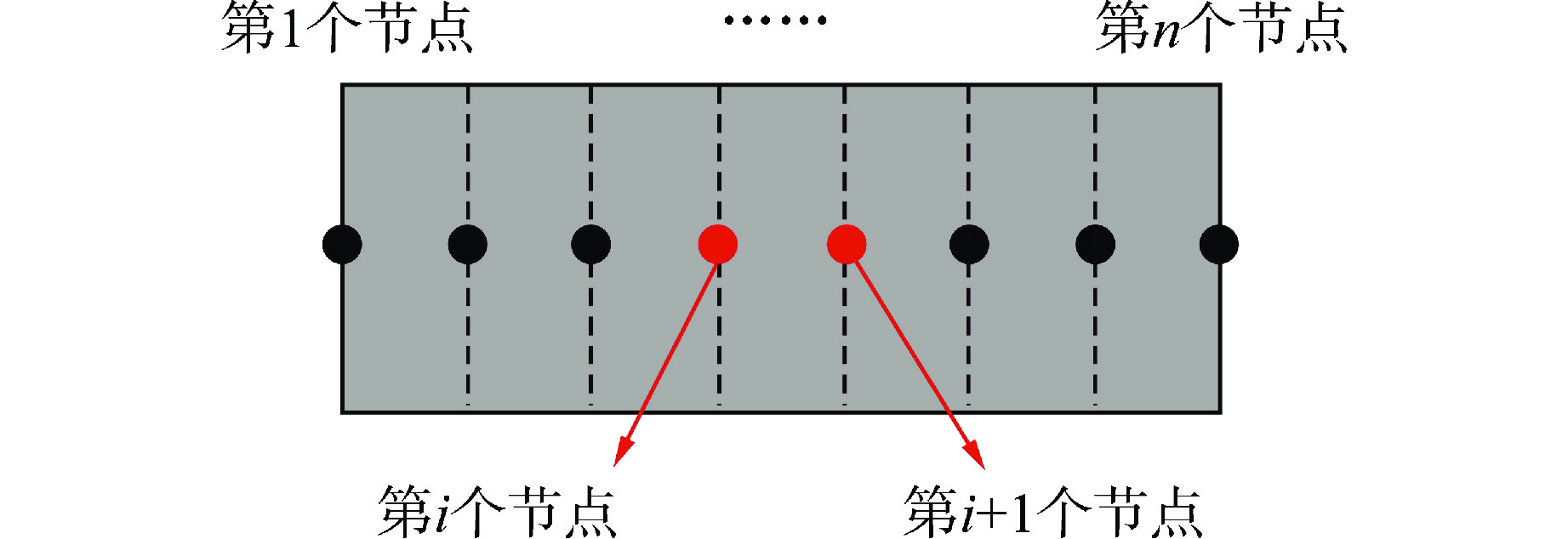
$$ -\dfrac{\nu_{r\text{z}}}{E_r}\dfrac{\text{d}\sigma_r}{\text{d}r}-\dfrac{\nu_{\theta\text{z}}}{E_{\theta}}\dfrac{\text{d}\sigma_{\theta}}{\text{d}r}+\dfrac{1}{E_{\text{z}}}\dfrac{\text{d}\sigma_{\text{z}}}{\text{d}r}+\dfrac{\text{d}\varepsilon_{\text{z}}^{^{{\prime}}}}{\text{d}r}=0 $$ (5) $$ \begin{gathered}- \dfrac{\text{d}\sigma_{\theta}}{\text{d}r} = \dfrac{E_{\theta}\left(1 - \nu_{r\text{z}}\nu_{{\textit{z}}\theta}\right)}{rE_r\left(1 - \nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_r + \dfrac{E_{\theta}\left(\nu_{r\theta} + \nu_{r\text{z}}\nu_{{\textit{z}}\theta}\right) - E_r\left(1+\nu_{\theta r}\right)}{rE_r\left(1 - \nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_{\theta}+ \\ \qquad \dfrac{E_{\theta}\left(\nu_{{\textit{z}}\theta}-\nu_{{\textit{z}}r}\right)}{rE_{\text{z}}\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_{\text{z}}+\dfrac{E_{\theta}\left(\varepsilon_r^{^{{\prime}}}-\varepsilon_{\theta}^{^{{\prime}}}\right)}{r\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}-\dfrac{E_{\theta}}{1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}}\dfrac{\text{d}\varepsilon_{\theta}^{^{{\prime}}}}{\text{d}r}- \\ \qquad \dfrac{E_{\theta}\nu_{{\textit{z}}\theta}}{1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}}\dfrac{\text{d}\varepsilon_{\text{z}}^{^{{\prime}}}}{\text{d}r} \dfrac{\text{d}\sigma_{\text{z}}}{\text{d}r}=\dfrac{E_{\text{z}}\left(\nu_{\theta\text{z}}-\nu_{r\text{z}}\right)}{rE_r\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_r+ \\ \qquad \dfrac{E_{\text{z}}E_{\theta}\left(\nu_{r\theta}\nu_{\theta\text{z}}+\nu_{r\text{z}}\right)-E_{\text{z}}E_r\left(\nu_{\theta\text{z}}+\nu_{\theta r}\nu_{\theta\text{z}}\right)}{rE_rE_{\theta}\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_{\theta}+ \\ \qquad \dfrac{\nu_{\theta\text{z}}\left(\nu_{{\textit{z}}\theta}-\nu_{{\textit{z}}r}\right)}{r\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}\sigma_{\text{z}}+\dfrac{\nu_{\theta\text{z}}E_{\text{z}}\left(\varepsilon_r^{^{{\prime}}}-\varepsilon_{\theta}^{^{{\prime}}}\right)}{r\left(1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}\right)}- \dfrac{E_{\text{z}}\nu_{\theta\text{z}}}{1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}}\dfrac{\text{d}\varepsilon_{\theta}^{^{{\prime}}}}{\text{d}r}- \\ \qquad \dfrac{E_{\text{z}}}{1-\nu_{\theta\text{z}}\nu_{{\textit{z}}\theta}}\dfrac{\text{d}\varepsilon_{\text{z}}^{^{{\prime}}}}{\text{d}r} \\ \end{gathered} $$ 对单层材料划分n个径向节点(图1),基于有限差分法,形成径向方向相邻节点间的应力关系,如式(6)所示,其中矩阵a和向量b中元素均可由材料物性参数及节点几何位置对式(5)进行差分处理得到,其中下标i为径向节点编号。对式(6)继续递推计算,即可获得任意节点处应力与边界节点应力关系。
$$ {\left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}} \\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}} \\ {{a_{31}}}&{{a_{32}}}&{{a_{33}}} \end{array}} \right]_i} \cdot {\left\{ \begin{gathered} {\sigma _r} \\ {\sigma _\theta } \\ {\sigma _{\textit{z}}} \\ \end{gathered} \right\}_i} + {\left\{ \begin{gathered} {b_1} \\ {b_2} \\ {b_3} \\ \end{gathered} \right\}_i} = {\left\{ \begin{gathered} {\sigma _r} \\ {\sigma _\theta } \\ {\sigma _{\textit{z}}} \\ \end{gathered} \right\}_{i + 1}} $$ (6) 1.2 边界条件
边界上的应力分量求解需要使用3个定解条件,包括2个边界条件和1个宏观力学平衡条件[11]。
1.2.1 内表面边界条件
如果第1个节点半径为0,即固体为实心,则为原点边界条件,在该位置径向应力与环向应力相等;若第1个节点半径不为0,即固体为空心,则为压力边界条件。
1.2.2 外表面边界条件
对于典型燃料包壳,外表面边界条件为冷却剂压力边界条件。
1.2.3 轴向宏观力学平衡条件
在轴向上,需要满足力学平衡,即每一个横截面上的应力与面积乘积的积分要与轴向所受宏观合力相等。由于燃料芯块和包壳具有多层结构,并且芯块和包壳可能发生接触,因此轴向力学平衡边界条件需要分情况进行讨论。
芯块和包壳未接触时则单独计算包壳或芯块,宏观轴向合力等于内外压差乘以元件横截面积,由式(7)可建立轴向合力与包壳各节点轴向应力的关系;芯块和包壳发生接触后,则将芯块和包壳作为整体计算轴向力,或根据接触压力获得轴向摩擦力,作为芯块和包壳轴向力的一部分进行计算。
$$ \iint_{ }^{ }\sigma_{\textit{z}}\text{d}A=F_{\textit{z}}=\sum\limits_{i=1}^{n-1}\left[\dfrac{\text{d}A_i}{2}\cdot\left(\sigma_{{{\textit{z}},i}}+\sigma_{ {{\textit{z}},i+1}}\right)\right] $$ (7) 式中,A为沿径向节点划分圆环的面积,m2;Fz为轴向合力,N。
通过式(6)的递推关系,可将一侧的边界条件转移至另一侧边界节点上,求解该节点应力,并递推至其他节点,完成整体力学计算。
1.3 复合包壳层间力学建模
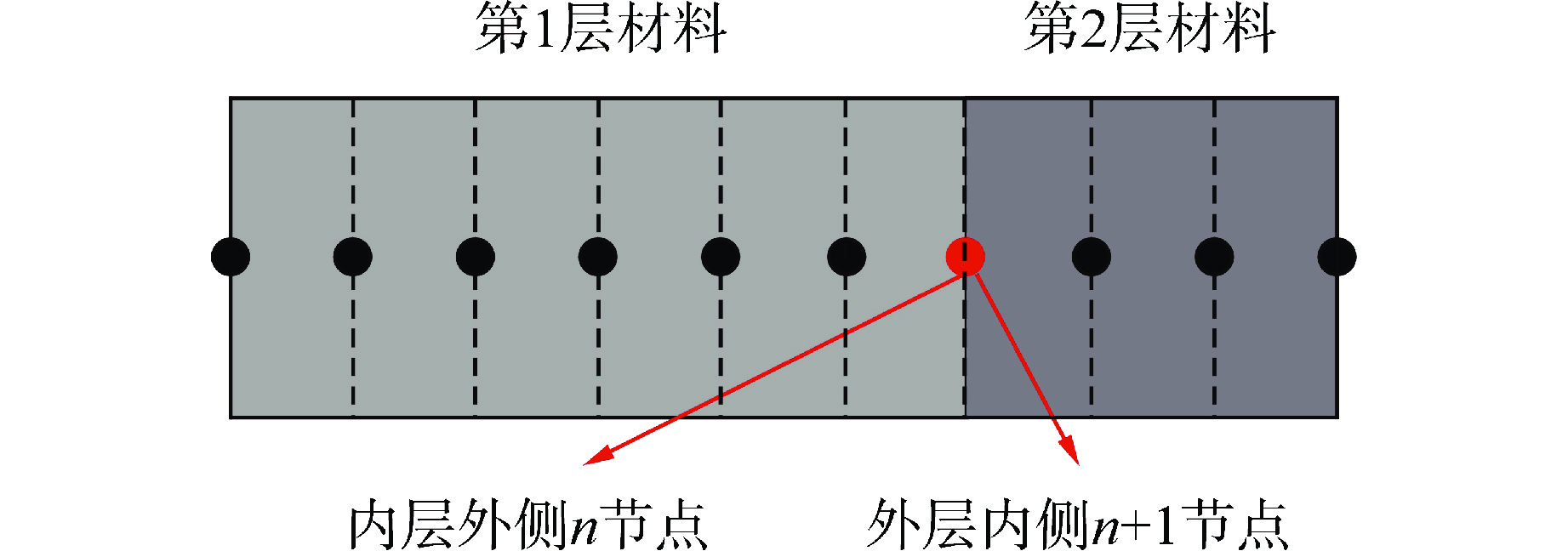
对于多层结构的复合材料,由于界面处材料性能、本征应变等不连续,即各物理量在界面处不可导,无法通过1.1节中的方法直接建立关系,需要对复合材料界面进行单独处理。对材料界面位置划分2个节点,这2个节点分别位于2层材料上,在空间位置上重合,但具有不同的材料性能和物理量,如图2所示。
在不考虑多层材料界面分离的情况下,始终满足以下力学关系:①径向应力相等;②空间位置重合;③环向和轴向变形一致。
$$ \left\{ \begin{gathered} {\sigma _{r,n}} = {\sigma _{r,n + 1}} \\ {\varepsilon _{\theta ,n}} = {\varepsilon _{\theta ,n + 1}} \\ {\varepsilon _{{\textit{z}},n}} = {\varepsilon _{{\textit{z}},n + 1}} \\ \end{gathered} \right. $$ (8) 为将界面处2个节点间的应力应变关系式(8)转换为式(6)的形式,将内外层的本构关系带入式(8),可得到第n+1个节点和第n个节点间的应力关系。完成层间关系建立后即可通过递推方式对多层包壳进行力学求解。
$$ \begin{split} & {\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ { - \dfrac{{{\nu _{r\theta ,n + 1}}}}{{{E_{r,n + 1}}}}}&{\dfrac{1}{{{E_{\theta ,n + 1}}}}}&{ - \dfrac{{{\nu _{{\textit{z}}\theta ,n + 1}}}}{{{E_{{\textit{z}},n + 1}}}}} \\ { - \dfrac{{{\nu _{r{\textit{z}},n + 1}}}}{{{E_{r,n + 1}}}}}&{ - \dfrac{{{\nu _{\theta {\textit{z}},n + 1}}}}{{{E_{\theta ,n + 1}}}}}&{\dfrac{1}{{{E_{{\textit{z}},n + 1}}}}} \end{array}} \right]} \left[ \begin{gathered} {\sigma _{r,n + 1}} \\ {\sigma _{\theta ,n + 1}} \\ {\sigma _{{\textit{z}},n + 1}} \\ \end{gathered} \right] = \\ &\quad \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ { - \dfrac{{{\nu _{r\theta ,n}}}}{{{E_{r,n}}}}}&{\dfrac{1}{{{E_{\theta ,n}}}}}&{ - \dfrac{{{\nu _{{\textit{z}}\theta ,n}}}}{{{E_{{\textit{z}},n}}}}} \\ { - \dfrac{{{\nu _{r{\textit{z}},n}}}}{{{E_{r,n}}}}}&{ - \dfrac{{{\nu _{\theta {\textit{z}},n}}}}{{{E_{\theta ,n}}}}}&{\dfrac{1}{{{E_{{\textit{z}},n}}}}} \end{array}} \right]\left[ \begin{gathered} {\sigma _{r,n}} \\ {\sigma _{\theta ,n}} \\ {\sigma _{{\textit{z}},n}} \\ \end{gathered} \right] + \left[ \begin{array}{*{20}{c}} 0 \\ \varepsilon {^{^{{\prime}}}_{\theta ,n}} - \varepsilon {^{^{{\prime}}}_{\theta ,n + 1}} \\ \varepsilon {^{^{{\prime}}}_{{\textit{z}},n}} - \varepsilon {^{^{{\prime}}}_{{\textit{z}},n + 1}} \\ \end{array} \right] \end{split} $$ (9) 1.4 芯块-包壳接触力学建模
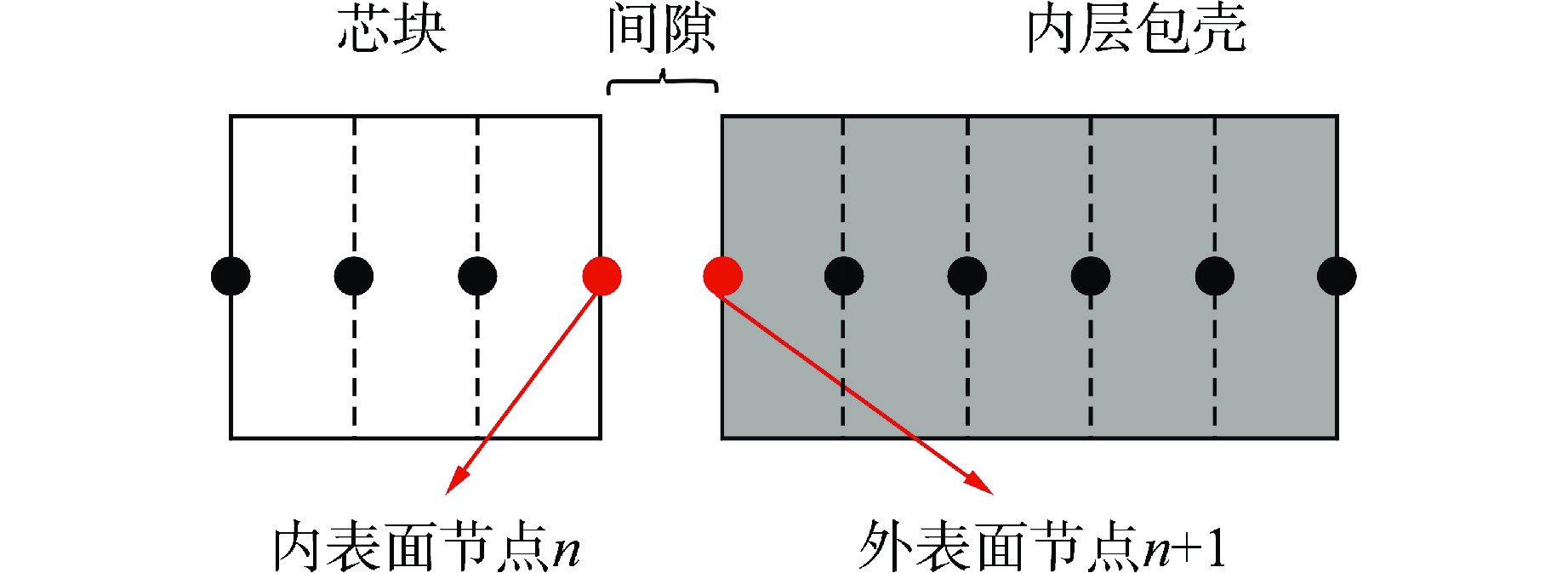
对于单独的芯块或多层包壳,可采用前文所述进行建模计算。然而在燃料棒运行过程中可能会发生PCMI,芯块与包壳发生接触后变形存在耦合作用,边界条件由压力边界条件转变为位移边界条件,需要作为整体进行联合求解。
芯块与包壳接触节点划分如图3所示。与式(8)形式类似,建立接触后的界面应力应变关系:①径向应力相等;②空间位置重合;③接触后的轴向变形一致。
$$ \left\{ \begin{gathered} {\sigma _{r,n}} = {\sigma _{r,n + 1}} \\ {r_n} \cdot \left( {1 + {\varepsilon _{\theta ,n}}} \right) = {r_{n + 1}} \cdot \left( {1 + {\varepsilon _{\theta ,n + 1}}} \right) \\ {\varepsilon _{{\textit{z}},n}} - \varepsilon _{{\textit{z}},n}^0 = {\varepsilon _{{\textit{z}},n + 1}} - \varepsilon _{{\textit{z}},n + 1}^0 \\ \end{gathered} \right. $$ (10) 式中,rn和rn+1分别为芯块和包壳接触节点初始半径;上标0表示发生接触的时刻。
同样将式(10)中的应变关系转换为应力关系,建立矩阵形式的两节点应力关系,即可对PCMI后芯块-包壳的应力应变进行整体求解。
$$ \begin{split} & {\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ { - \dfrac{{{\nu _{r\theta ,n + 1}}}}{{{E_{r,n + 1}}}}}&{\dfrac{1}{{{E_{\theta ,n + 1}}}}}&{ - \dfrac{{{\nu _{{\textit{z}}\theta ,n + 1}}}}{{{E_{{\textit{z}},n + 1}}}}} \\ { - \dfrac{{{\nu _{r{\textit{z}},n + 1}}}}{{{E_{r,n + 1}}}}}&{ - \dfrac{{{\nu _{\theta {\textit{z}},n + 1}}}}{{{E_{\theta ,n + 1}}}}}&{\dfrac{1}{{{E_{{\textit{z}},n + 1}}}}} \end{array}} \right] } \left[ \begin{gathered} {\sigma _{r,n + 1}} \\ {\sigma _{\theta ,n + 1}} \\ {\sigma _{{\textit{z}},n + 1}} \\ \end{gathered} \right] =\\ &\qquad \left[ {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\dfrac{{{r_n}}}{{{r_{n + 1}}}}}&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0&0 \\ { - \dfrac{\nu }{E}}&{\dfrac{1}{E}}&{ - \dfrac{\nu }{E}} \\ { - \dfrac{\nu }{E}}&{ - \dfrac{\nu }{E}}&{\dfrac{1}{E}} \end{array}} \right]\left[ \begin{gathered} {\sigma _{r,n}} \\ {\sigma _{\theta ,n}} \\ {\sigma _{{\textit{z}},n}} \\ \end{gathered} \right] + \\ &\qquad \left[ \begin{array}{c} 0 \\ \dfrac{{{r_n}}}{{{r_{n + 1}}}}\left( {1 + \varepsilon {^{^{{\prime}}}_{\theta ,n}}} \right) - \left( {1 + \varepsilon {^{^{{\prime}}}_{\theta ,n + 1}}} \right) \\ \varepsilon _{{\textit{z}},n + 1}^0 - \varepsilon _{{\textit{z}},n}^0 + \varepsilon {^{^{{\prime}}}_{{\textit{z}},n}} - \varepsilon {^{^{{\prime}}}_{{\textit{z}},n + 1}} \\ \end{array} \right] \\[-58pt] \end{split} $$ (11) 2. 模型应用与验证
2.1 FRAPCON 4.0程序改进
FRAPCON是美国核管会用于轻水堆燃料性能分析的主要工具,具有速度快、可靠性高、鲁棒性强等优点。该程序已通过大量堆内外实验数据的验证,广泛应用于燃料性能分析与安全评审。
本研究基于西安交通大学二次开发的FRAPCON-SiC[12-13]程序,将上述开发的力学模型植入,在计算中替换原机械力学计算模块。并在原本各向同性材料模型和多层包壳模型的基础上,增加了CMC型SiC的各向异性力学模型和多轴类塑性模型。改进后的FRAPCON程序在力学计算部分计算量有所增加,但仍保持了FRAPCON程序的计算速度快、稳定性强等优势,计算耗时远小于BISON、ABAQUS等精细有限元计算工具,可用于大规模分析计算和优化设计等。
2.2 模型验证
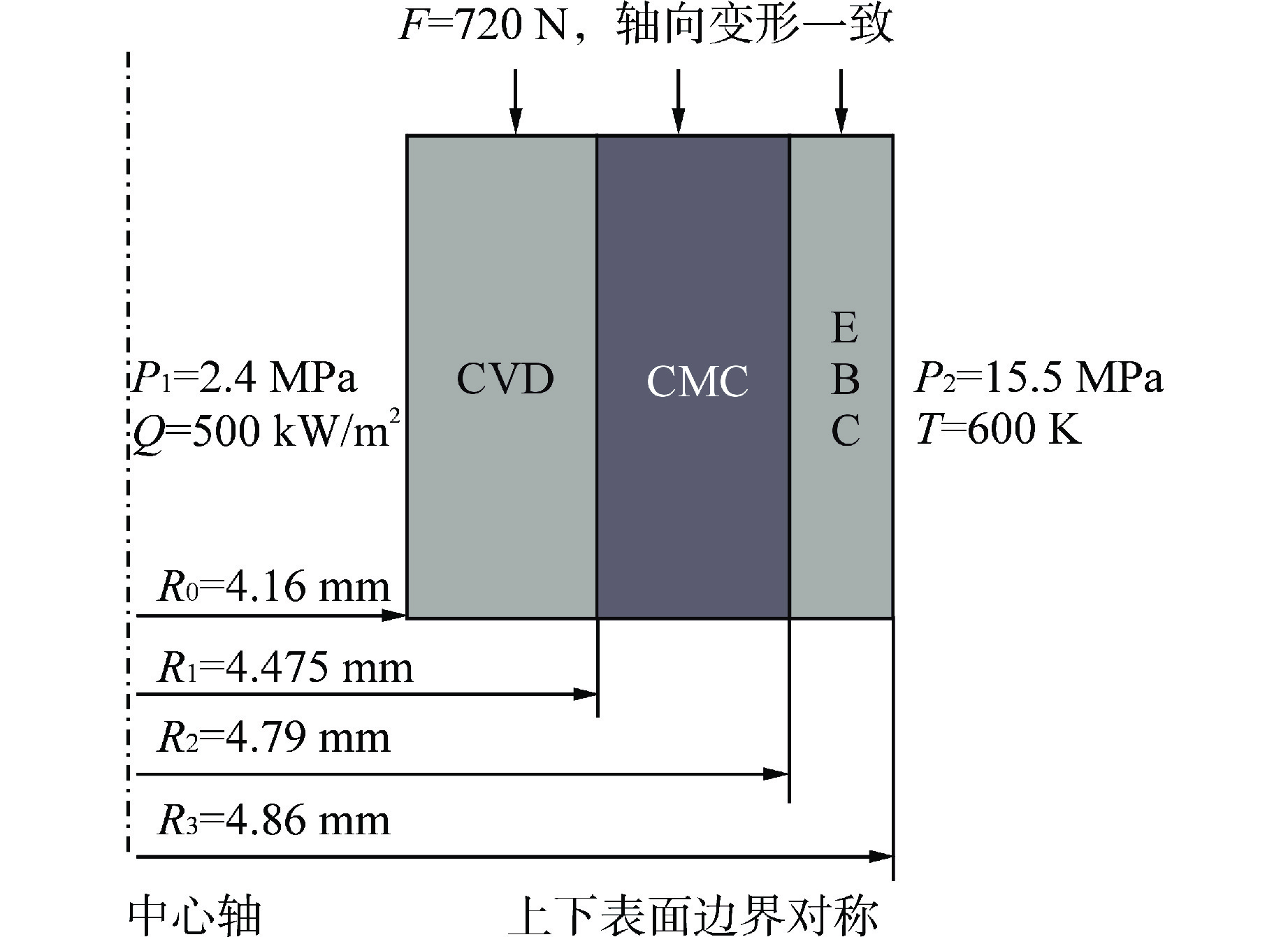
为验证模型开发的正确性,采用3层SiC包壳结构作为计算对象,分别使用本研究中开发的力学模型和商用有限元计算软件ABAQUS计算在热力耦合作用下的应力应变。算例对象及边界条件如图4所示,其中,R0、R3分别为包壳内外表面半径;R1、R2为多层包壳界面位置半径;P1、P2分别为包壳内、外表面压力;Q为径向热流密度;T为包壳外表面温度;F为轴向压力。采用的SiC材料力学参数如表1所示,EBC层采用CVD型SiC物性。
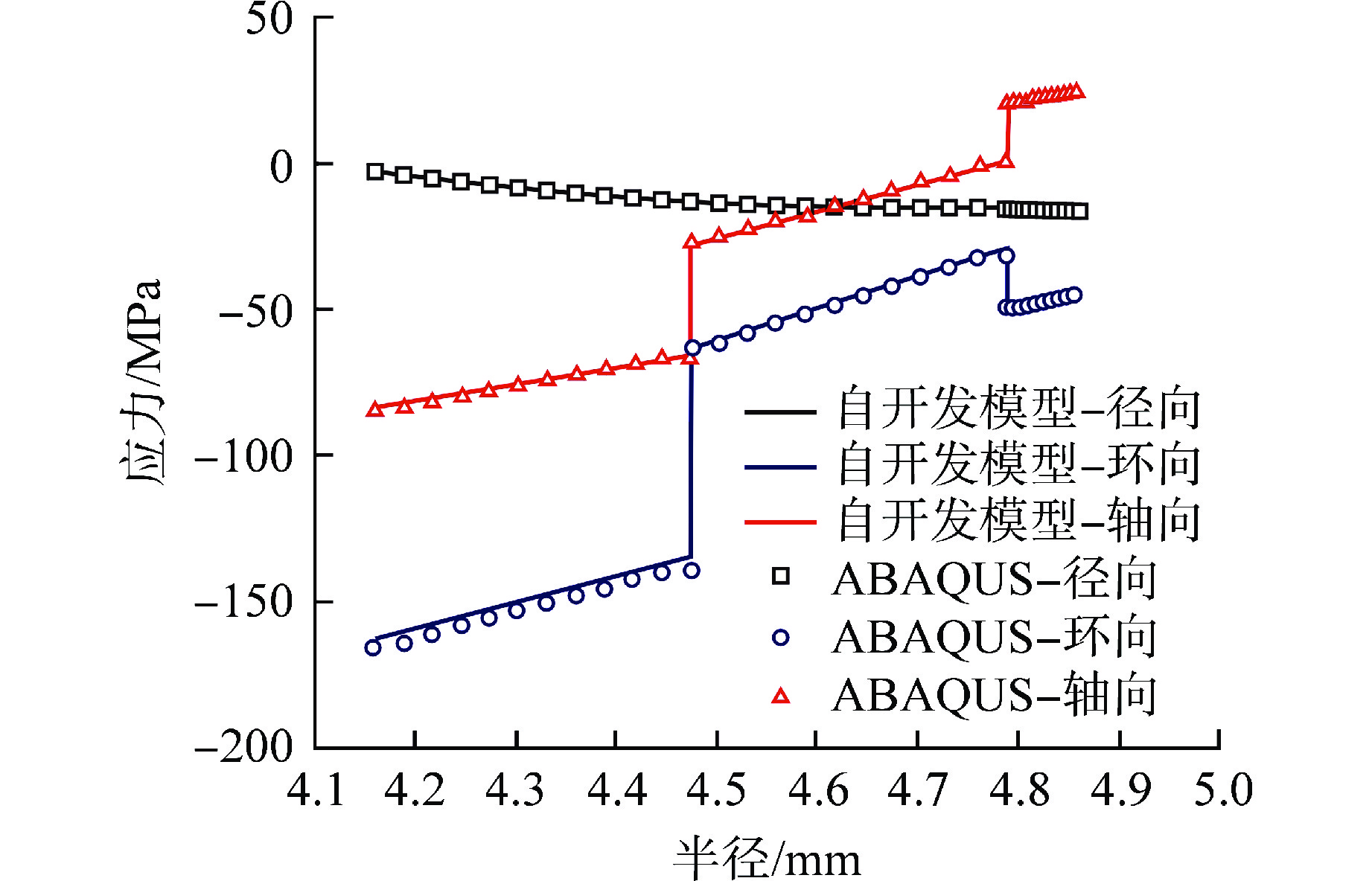
表 1 验证算例采用的CMC及CVD型SiC材料参数Table 1. Material Prameters of CMC and CVD SiC in Validation Case材料 参数 数值 CMC型SiC Er/GPa 95.5 Eθ/GPa 201 Ez/GPa 173 νrθ 0.248 νrz 0.242 νθz 0.175 G/GPa 62.4 热导率/(W·m–1·K−1) 2 热膨胀系数 2×10−6 CVD型SiC E/GPa 460 ν 0.21 热导率/(W·m–1·K−1) 10 热膨胀系数 2×10−6 图5为应力计算结果对比,在各层界面上的环向应力和轴向应力均存在突变。程序计算结果与ABAQUS软件计算结果符合良好,少许差异由建模和数值求解方法不同引起,证明了模型适用于各向异性材料多层复合结构的力学分析。
3. 堆内性能模拟
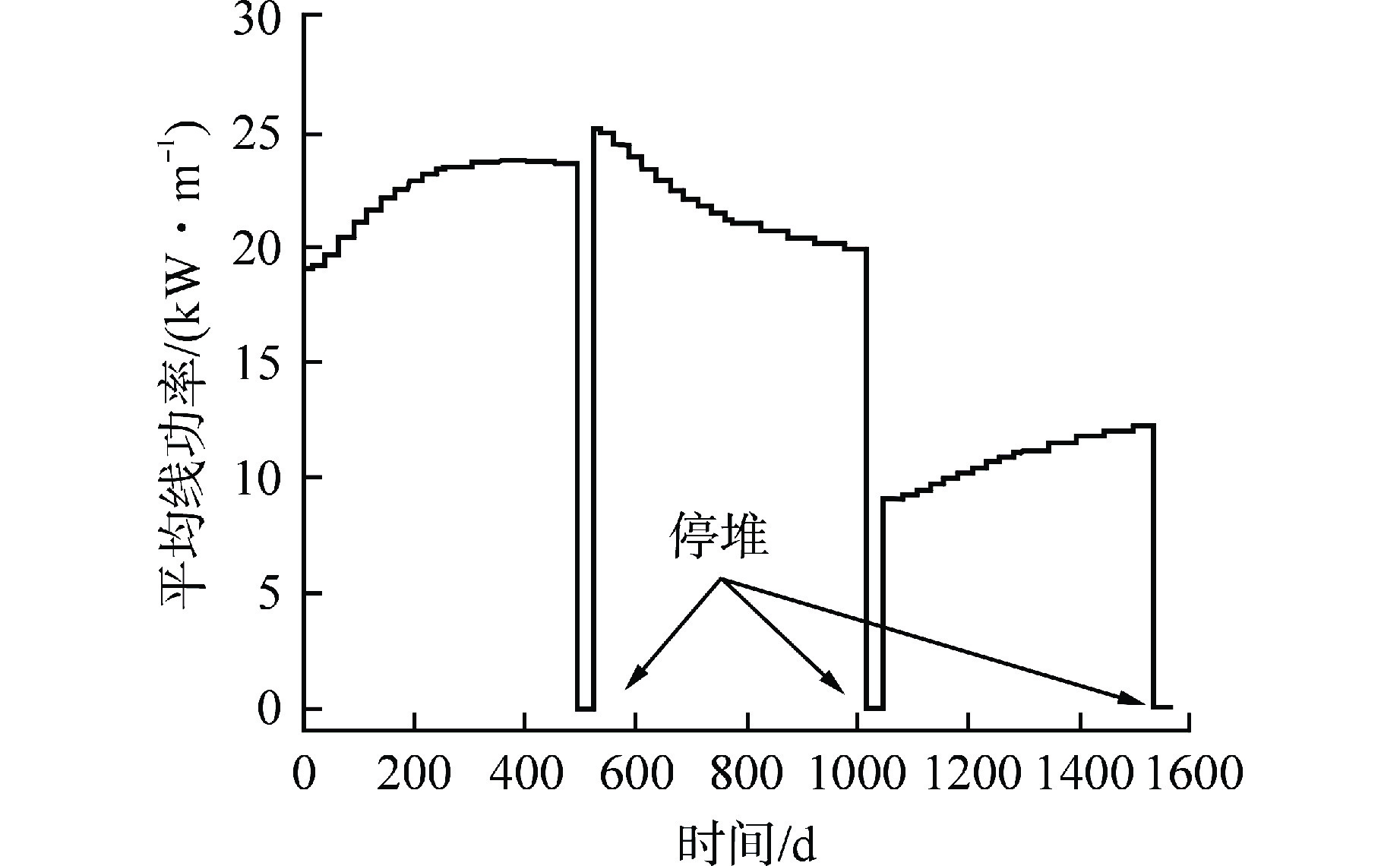
使用改进后的FRAPCON程序对CMC/CVD双层SiC复合包壳燃料棒稳态运行性能进行计算,并与Zr-4包壳燃料棒进行对比。部分关键运行条件和燃料棒设计参数如表2所示,功率历史如图6所示。
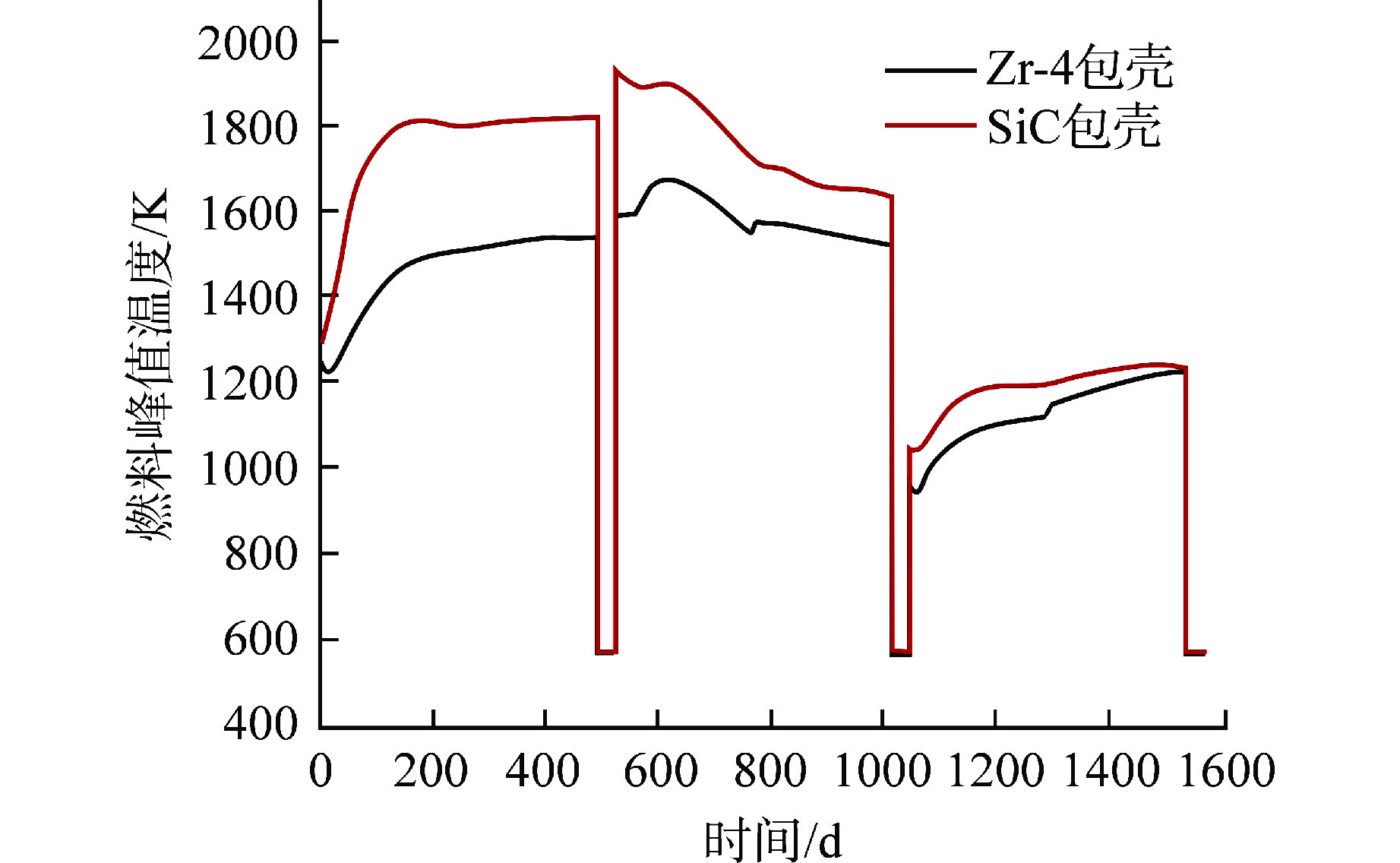
表 2 燃料棒设计参数和运行条件Table 2. Design Parameters and Operation Conditions of Fuel Rod参数 数值 Zr-4包壳外径/mm 9.48 Zr-4包壳厚度/mm 0.56 SiC包壳外径/mm 9.76 SiC包壳(CMC/CVD)厚度/mm 0.45/0.25 芯块直径/mm 8.192 活性区高度/m 3.6576 气腔长度/m 0.175 初始内压/MPa 2.41 冷却剂压力/MPa 15.51 冷却剂入口温度/K 565.7 冷却剂质量流量/(kg·m–2·s−1) 3434.5 燃料峰值温度随时间变化曲线如图7所示,2种包壳燃料棒燃料温度变化趋势基本相同,但由于SiC辐照后热导率迅速降低,且气隙宽度更大,运行较短时间后其燃料温度显著高于Zr-4包壳燃料棒。
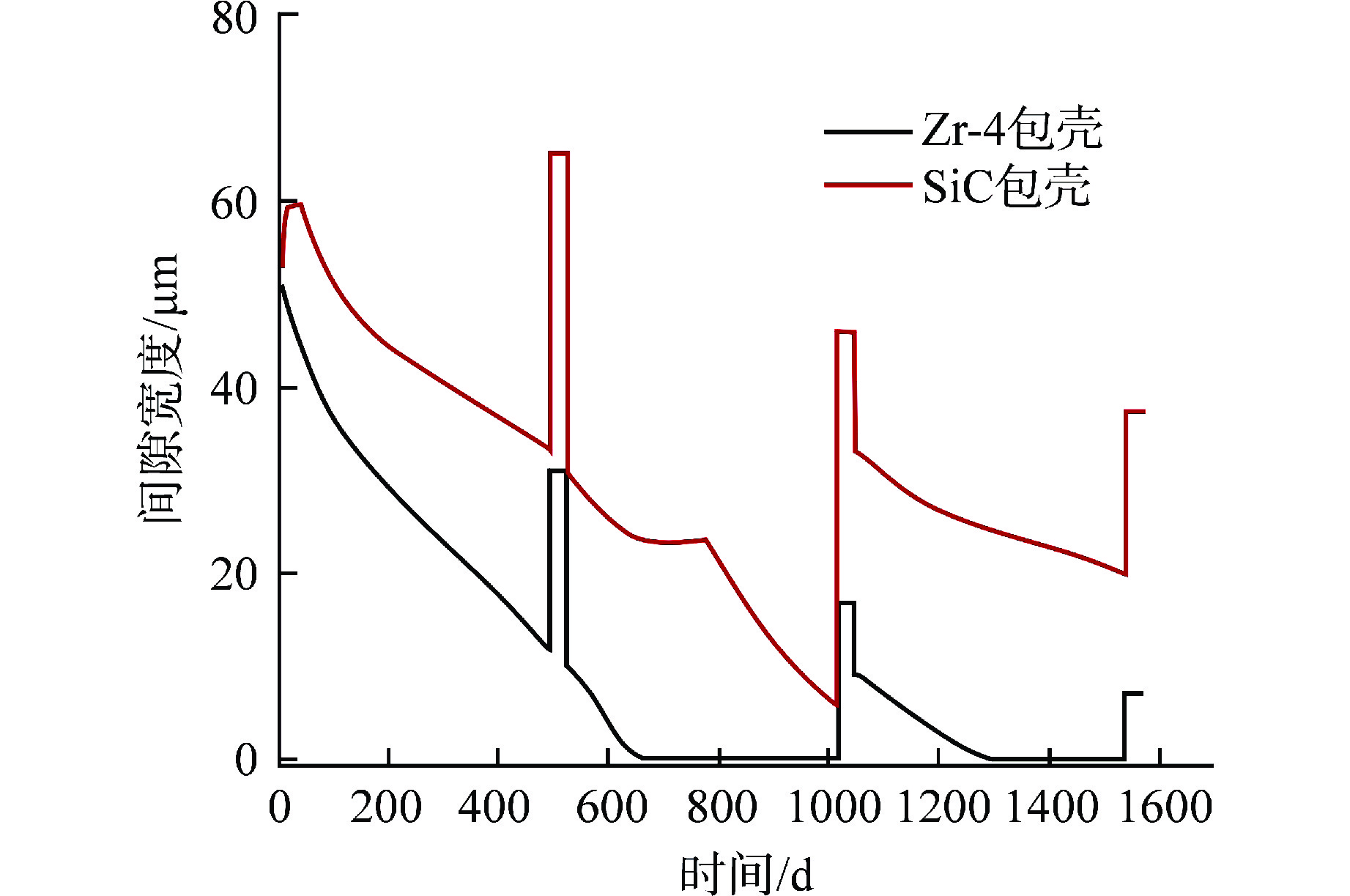
间隙宽度对比如图8所示,SiC包壳燃料棒间隙远大于同时期Zr-4包壳中的间隙,其在整个运行期间未出现闭合,而Zr-4包壳在第2和第3循环后期发生了PCMI。造成SiC包壳燃料中的气隙宽度相对Zr-4包壳更大的因素有2个:①SiC包壳投入运行后,迅速发生辐照肿胀,造成包壳尺寸变大,而Zr-4包壳在辐照中没有辐照肿胀发生;②SiC包壳蠕变速率几乎可以忽略,不会在外部冷却剂压力下发生蠕变坍塌,而此现象是在Zr-4包壳变形中的重要因素。
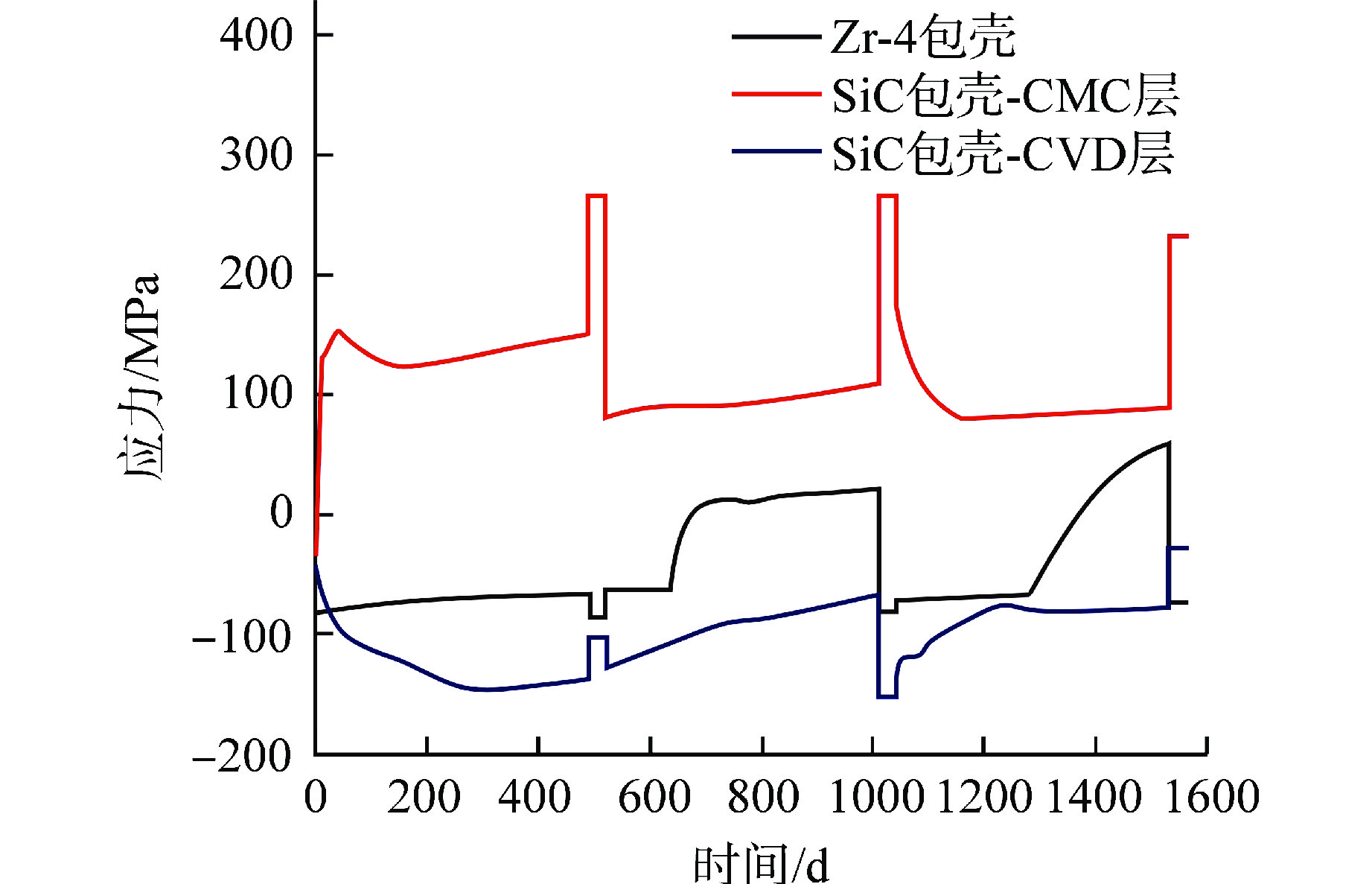
包壳环向应力对比如图9所示,Zr-4包壳最大的环向应力发生在PCMI阶段,其他时间由于内压始终小于冷却剂压力,其环向应力为负。而SiC包壳未发生PCMI,CMC层最大应力发生在停堆期间,主要是由于辐照肿胀梯度引起的。CMC层应力为正,但处于较低水平,运行期间始终小于150 MPa,停堆期间最大值约为265 MPa,小于其极限抗拉强度,而CVD层环向应力始终为负,保证了包壳的气密性和结构完整性。
4. 各向异性力学模型的潜在应用
当前工程应用的典型燃料性能分析程序(如FRAPCON、FRAPTRAN、TRANSURANUS、COPERNIC等)中力学模型通常采用各项同性、薄壁包壳等假设,对于新型材料及结构(如复合包壳、各向异性材料、多孔材料等)不适用。而基于有限元方法的三维精细燃料分析程序(如BISON、BEEs)虽然能够对复杂燃料结构进行模拟,但难以满足工程应用的计算速度和稳定性要求。本研究建立的力学模型采用有限差分法求解,在保持计算速度和稳定性的基础上,扩展了燃料性能分析程序可建模的材料和结构范围,具有较大应用前景。
(1)多层各向异性材料建模。本模型可应用于任意多层圆柱结构,并且考虑材料各向异性物性的燃料元件建模,例如SiCf/SiC材料、泡沫金属材料等。
(2)各向异性行为模拟。某些材料虽然其初始为各向同性材料,但在运行期间可能表现出某些各向异性行为,如各向异性肿胀、孔隙、裂纹分布等。本模型可考虑各向异性行为对材料性能产生的影响。
(3)ATF设计与优化研究。基于本模型改进的燃料性能分析程序保持了较快的计算速度,可用于ATF设计中大规模的敏感性分析、全堆芯计算、优化设计等。
5. 结 论
本研究针对各向异性SiC复合包壳,开发了适用于多层各向异性材料的1.5维轴对称力学模型,并将该模型植入FRAPCON4.0程序后对SiC包壳燃料元件堆内性能进行计算分析,得到如下结论:
(1)本研究中建立的模型具有较强通用性,可用于建立任意多层结构、任意材料(包括正交各向异性材料)的圆柱结构燃料元件模型。
(2)模型可用于采用新型结构或材料的燃料元件分析计算,特别是当前ATF设计中涂层包壳、SiC复合包壳、掺杂芯块材料等分析。
(3)开发了针对各向异性SiC复合包壳的分析程序,对模型进行了验证,改进了SiC复合包壳燃料元件的堆内性能分析工具。
-
表 1 验证算例采用的CMC及CVD型SiC材料参数
Table 1. Material Prameters of CMC and CVD SiC in Validation Case
材料 参数 数值 CMC型SiC Er/GPa 95.5 Eθ/GPa 201 Ez/GPa 173 νrθ 0.248 νrz 0.242 νθz 0.175 G/GPa 62.4 热导率/(W·m–1·K−1) 2 热膨胀系数 2×10−6 CVD型SiC E/GPa 460 ν 0.21 热导率/(W·m–1·K−1) 10 热膨胀系数 2×10−6 表 2 燃料棒设计参数和运行条件
Table 2. Design Parameters and Operation Conditions of Fuel Rod
参数 数值 Zr-4包壳外径/mm 9.48 Zr-4包壳厚度/mm 0.56 SiC包壳外径/mm 9.76 SiC包壳(CMC/CVD)厚度/mm 0.45/0.25 芯块直径/mm 8.192 活性区高度/m 3.6576 气腔长度/m 0.175 初始内压/MPa 2.41 冷却剂压力/MPa 15.51 冷却剂入口温度/K 565.7 冷却剂质量流量/(kg·m–2·s−1) 3434.5 -
[1] TERRANI K A. Accident tolerant fuel cladding development: promise, status, and challenges[J]. Journal of Nuclear Materials, 2018, 501: 13-30. [2] KATOH Y, OZAWA K, SHIH C, et al. Continuous SiC fiber, CVI SiC matrix composites for nuclear applications: properties and irradiation effects[J]. Journal of Nuclear Materials, 2014, 448(1-3): 448-476. [3] LEE Y, KAZIMI M S. A structural model for multi-layered ceramic cylinders and its application to silicon carbide cladding of light water reactor fuel[J]. Journal of Nuclear Materials, 2015, 458: 87-105. [4] KATOH Y, SNEAD L L. Silicon carbide and its composites for nuclear applications - Historical overview[J]. Journal of Nuclear Materials, 2019, 526: 151849. [5] SNEAD L L, NOZAWA T, KATOH Y, et al. Handbook of SiC properties for fuel performance modeling[J]. Journal of Nuclear Materials, 2007, 371(1-3): 329-377. [6] KATOH Y, NOZAWA T, SNEAD L L, et al. Stability of SiC and its composites at high neutron fluence[J]. Journal of Nuclear Materials, 2011, 417(1-3): 400-405. [7] SUKJAI Y. Silicon carbide performance as cladding for advanced uranium and thorium fuels for light water reactors[D]. Cambridge: Massachusetts Institute of Technology, 2014. [8] BEN-BELGACEM M, RICHET V, TERRANI K A, et al. Thermo-mechanical analysis of LWR SiC/SiC composite cladding[J]. Journal of Nuclear Materials, 2014, 447(1-3): 125-142. [9] DENG Y B, SHIRVAN K, WU Y W, et al. Probabilistic view of SiC/SiC composite cladding failure based on full core thermo-mechanical response[J]. Journal of Nuclear Materials, 2018, 507: 24-37. [10] RHO H, LEE Y. Development of a 2D axisymmetric SiC cladding mechanical model and its applications for steady-state and LBLOCA analysis[J]. Journal of Nuclear Materials, 2022, 558: 153311. [11] 邓阳斌,贺亚男,巫英伟,等. 多层结构包壳和非刚体芯块力学建模及应用[J]. 原子能科学技术,2018, 52(7): 1308-1315. doi: 10.7538/yzk.2017.youxian.0611 [12] DENG Y B, WU Y W, QIU B W, et al. Development of a new Pellet-Clad Mechanical Interaction (PCMI) model and its application in ATFs[J]. Annals of Nuclear Energy, 2017, 104: 146-156. [13] HE Y N, SHIRVAN K, WU Y W, et al. Fuel performance optimization of U3Si2-SiC design during normal, power ramp and RIA conditions[J]. Nuclear Engineering and Design, 2019, 353: 110276. 期刊类型引用(1)
1. 刘华年,王静,李超群. 基于多重网格法的多晶各向异性轴承钢热弹流润滑耦合算法. 摩擦学学报(中英文). 2025(01): 58-66 .  百度学术
百度学术其他类型引用(0)
-







 下载:
下载:









 下载:
下载:








 百度学术
百度学术