Validation of HPR1000 Core Modeling and Startup Test with Three-dimensional Characteristic Neutronics Calculation Code SHARK
-
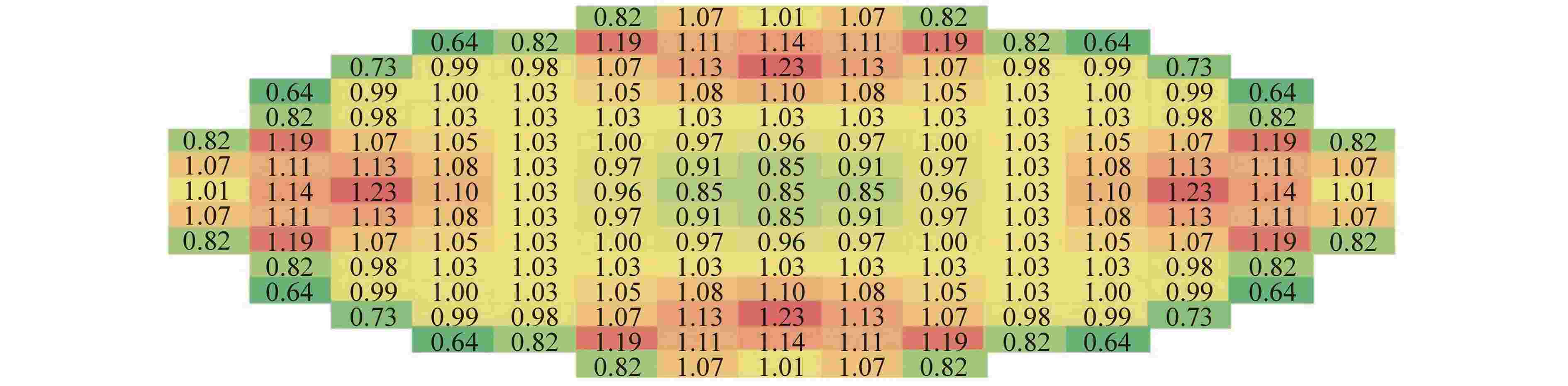
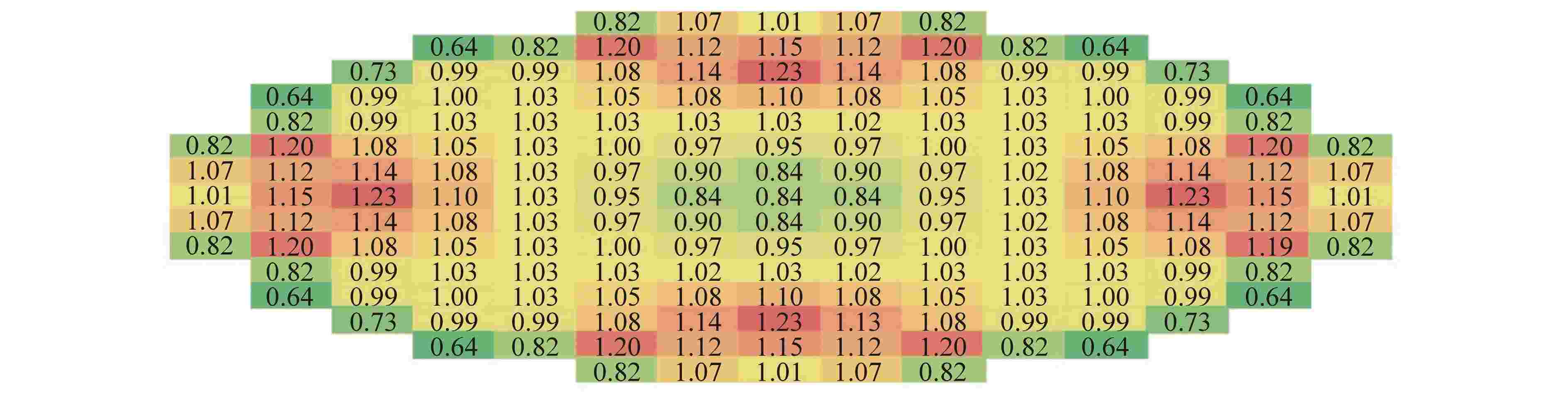
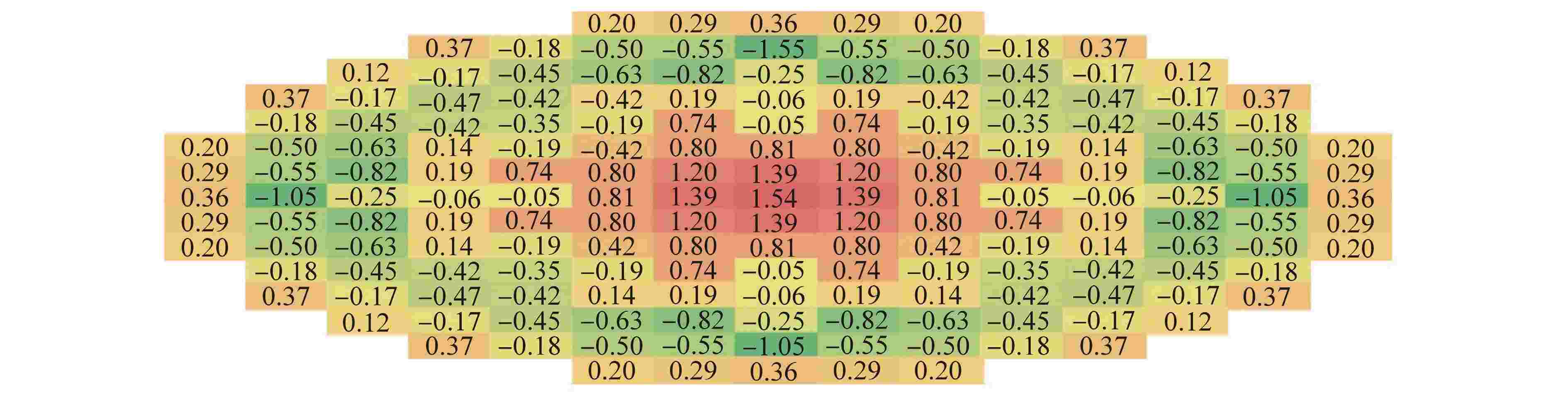
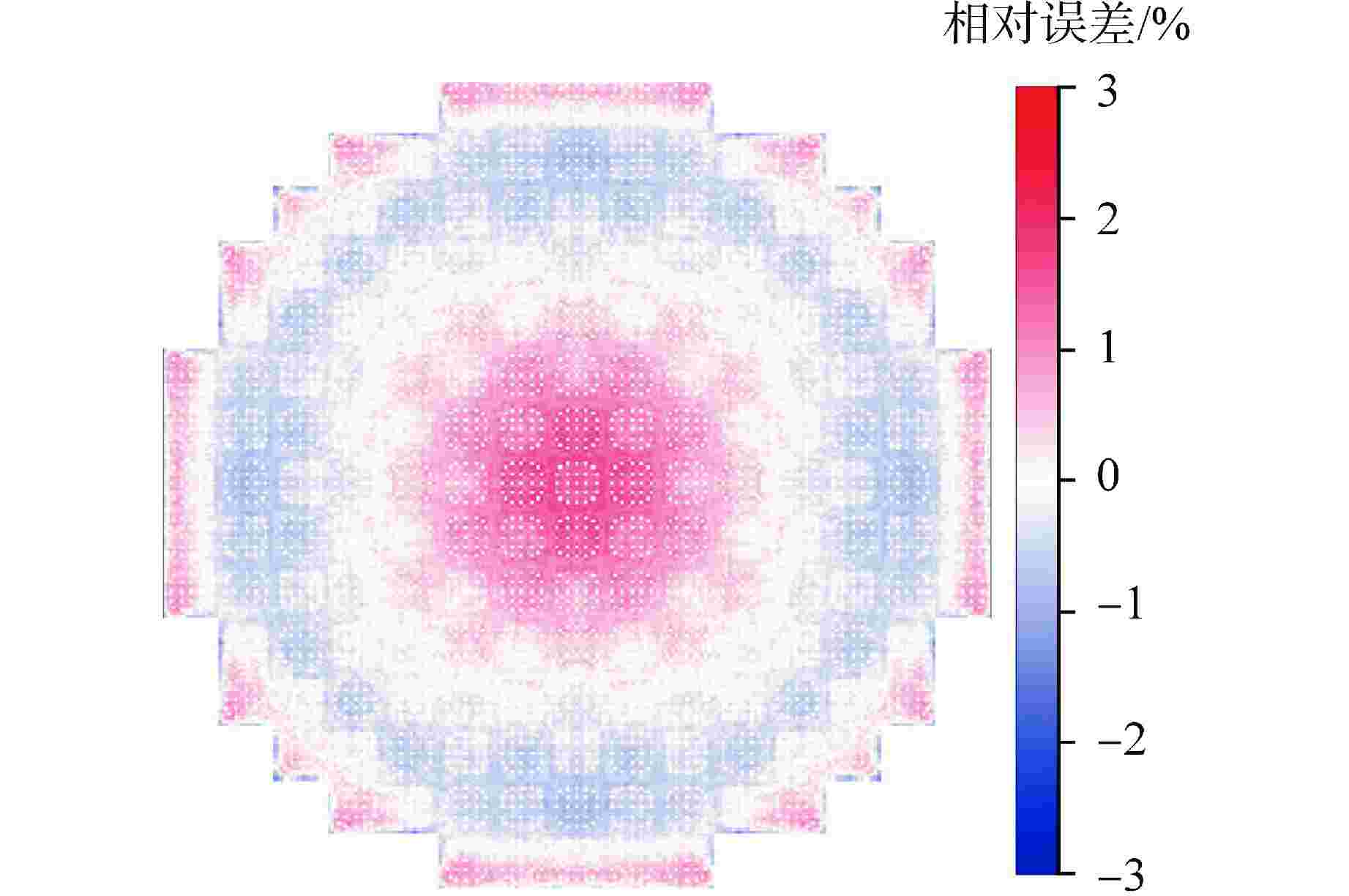
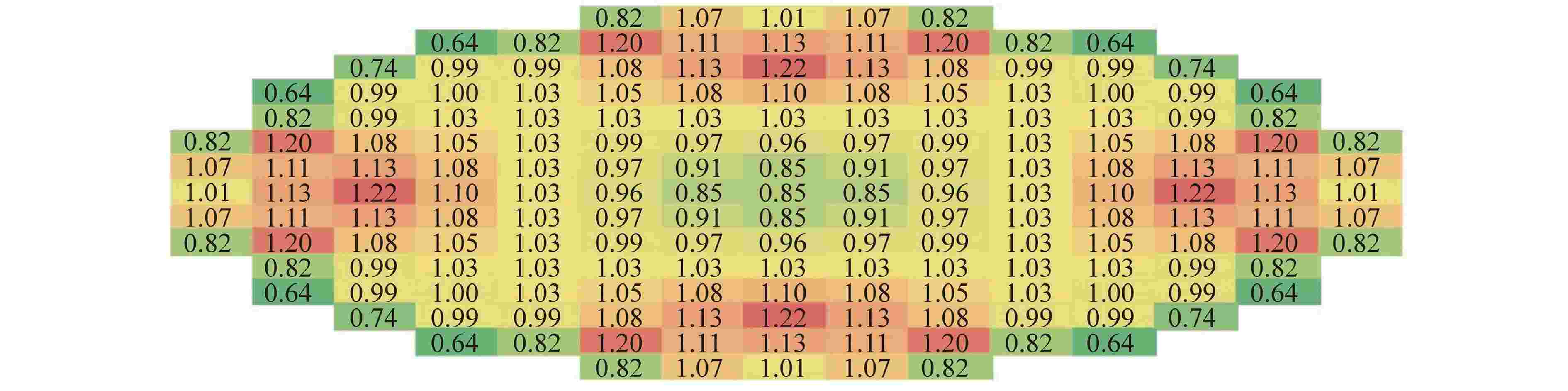
摘要: 为验证三维特征线中子学计算程序SHARK在大型压水堆上的准确性和适用性，以华龙一号的启动物理试验对SHARK程序进行验证。华龙一号是我国具有自主知识产权的三代核电压水堆堆型，验证内容包括临界有效增殖系数keff、控制棒积分价值以及组件功率分布。研究结果表明，临界有效增殖系数keff、组件功率分布结果与控制棒积分价值均与实测值符合良好。因此SHARK能够应用于数字化反应堆物理计算，具有良好的计算精度。Abstract: To validate the accuracy and applicability of the three-dimensional characteristic neutronics calculation code SHARK for large PWRs, the startup test of HPR1000 is selected. The HPR1000 is a third-generation nuclear pressurized water reactor with independent intellectual property rights in China. The validation contents include critical effective multiplication coefficient keff, control rod integral value and assembly power distribution. The results show that the critical effective multiplication coefficient keff, assembly power distribution and control rod integral value are in good agreement with the measured values. Therefore, the code SHARK can be applied to the physical calculation of digital reactors with good calculation accuracy.
-
Key words:
- Digital reactor /
- HPR1000 /
- SHARK /
- Startup test
-
图 3 华龙一号首循环堆芯装载和可燃毒物棒布置图
18000—富集度1.8%；24000—富集度为2.4%，不含硼可燃毒物棒；24012—富集度为2.4%，含12根硼可燃毒物棒；24016—富集度为2.4%，含16根硼可燃毒物棒；24020—富集度为2.4%，含20根硼可燃毒物棒；31000—富集度为3.1%，不含硼可燃毒物棒；31008—富集度为3.1%，含8根硼可燃毒物棒；31016—富集度为3.1%，含16根硼可燃毒物棒
Figure 3. Layout for the First Cycle and Burnable Poison of HPR1000
图 4 华龙一号首循环控制棒布置图
SA、SB、SC—停堆棒组；G1、G2、N1、N2—功率补偿棒组；R—温度调节棒组
Figure 4. Layout of Control Rod for the First Cycle of HPR1000
图 7 SHARK堆芯功率分布（BOL、HZP、0Xe、ARO）
Figure 7. Core Power Distribution of SHARK (BOL, HZP, 0Xe, ARO)
图 8 RMC堆芯功率分布（BOL、HZP、0Xe、ARO）
Figure 8. Core Power Distribution of RMC (BOL, HZP, 0Xe, ARO)
图 9 组件功率相对偏差（BOL、HZP、0Xe、ARO）
Figure 9. Assembly Power Difference (BOL, HZP, 0Xe, ARO)
图 13 SHARK与实测值组件功率相对偏差
Figure 13. Assembly Power Distribution Difference between SHARK and Measured Value
表 1 SHARK数值离散计算参数
Table 1. SHARK Numerical Discrete Calculation Parameters
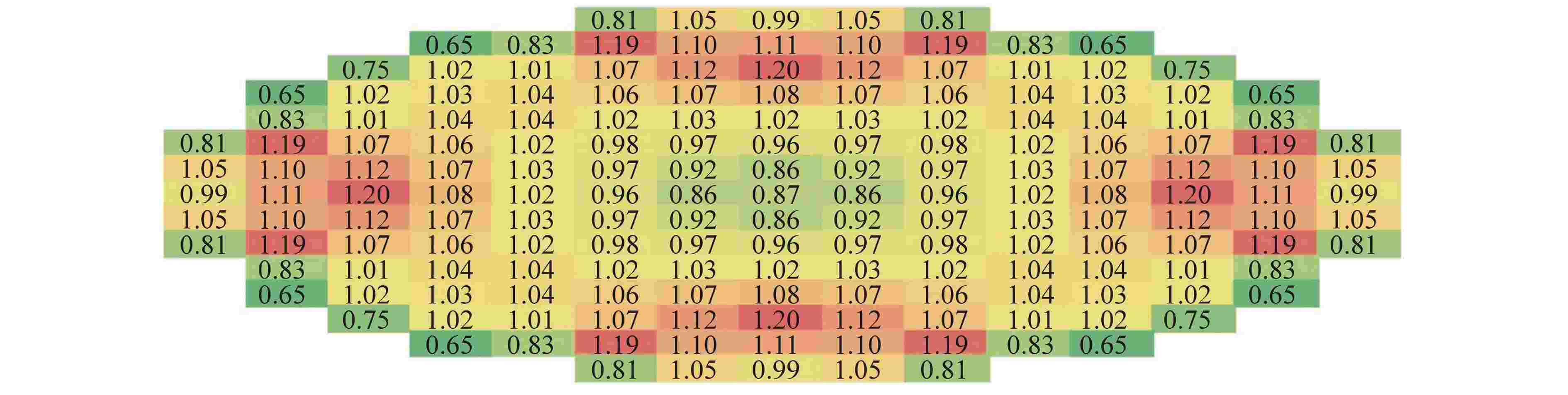
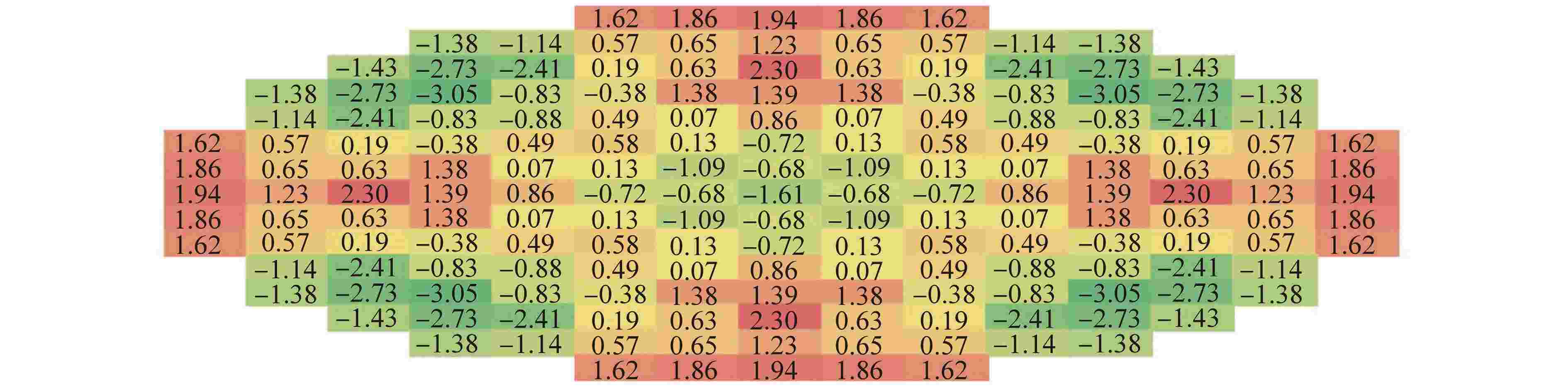
参数 数值 燃料芯块圈数 2 燃料栅元中包壳圈数 1 燃料栅元中冷却剂圈数 1 周向划分个数 4 辐角个数 32 极角个数 6 特征线宽/cm 0.03 裂变率收敛限 10−4 keff收敛限/pcm 1 径向并行区域分解数 289 轴向并行区域分解数 18 能群 45 平源区数量 51598888 1pcm=10−5 
下载: 导出CSV
表 2 临界结果比较
Table 2. Comparison of Critical Results
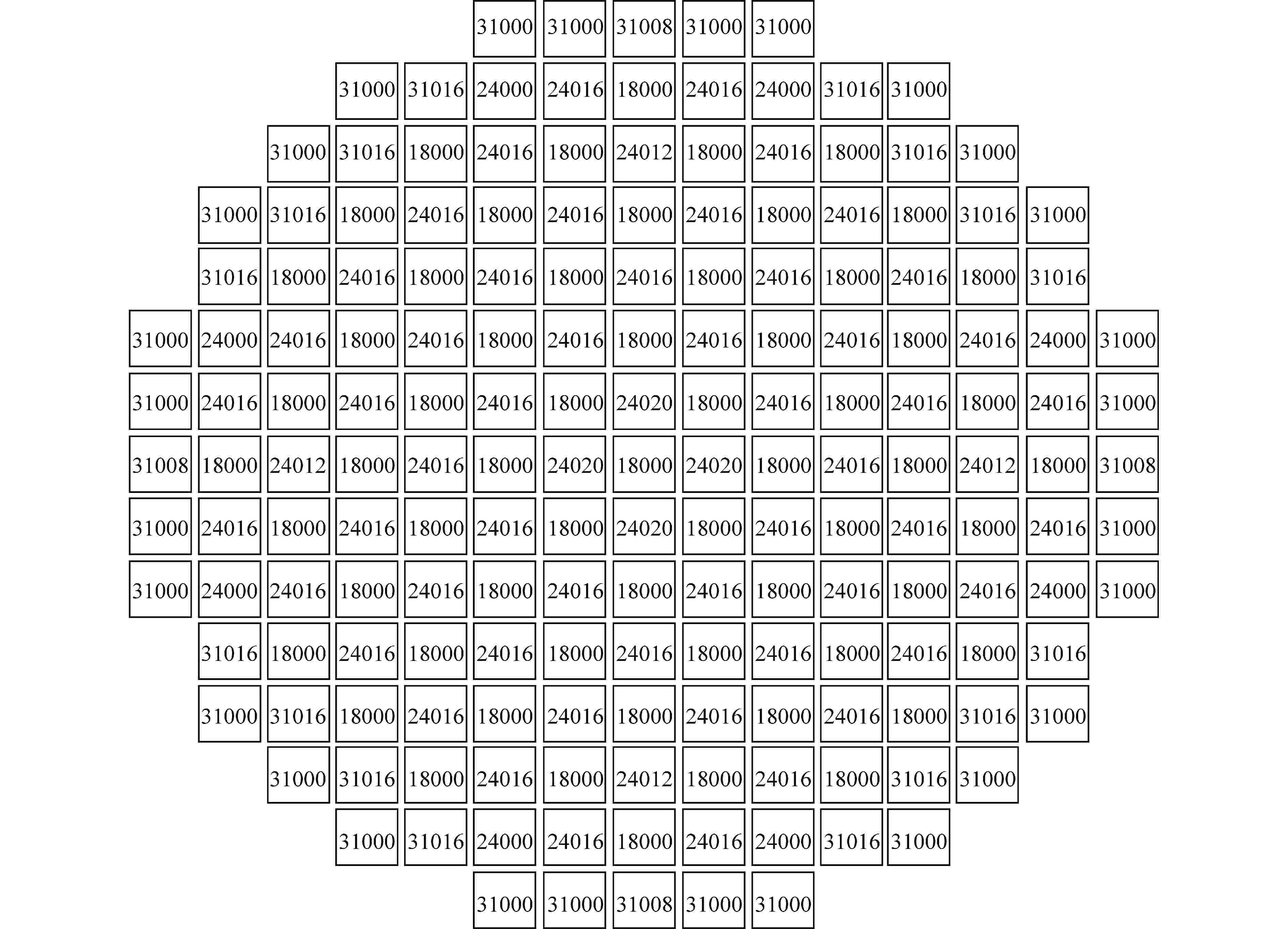
状态 实测临界硼浓度值/ppm SHARK计算的 keff 偏差/pcm ARO 1074.9 0.99843 −157 RG1in 932.2 0.99681 −319 Rin 967.7 0.99720 −280 ppm=μg/g
下载: 导出CSV
表 3 控制棒组积分价值结果与偏差比较
Table 3. Comparison of Control Rod Worth Results and Relative Deviation
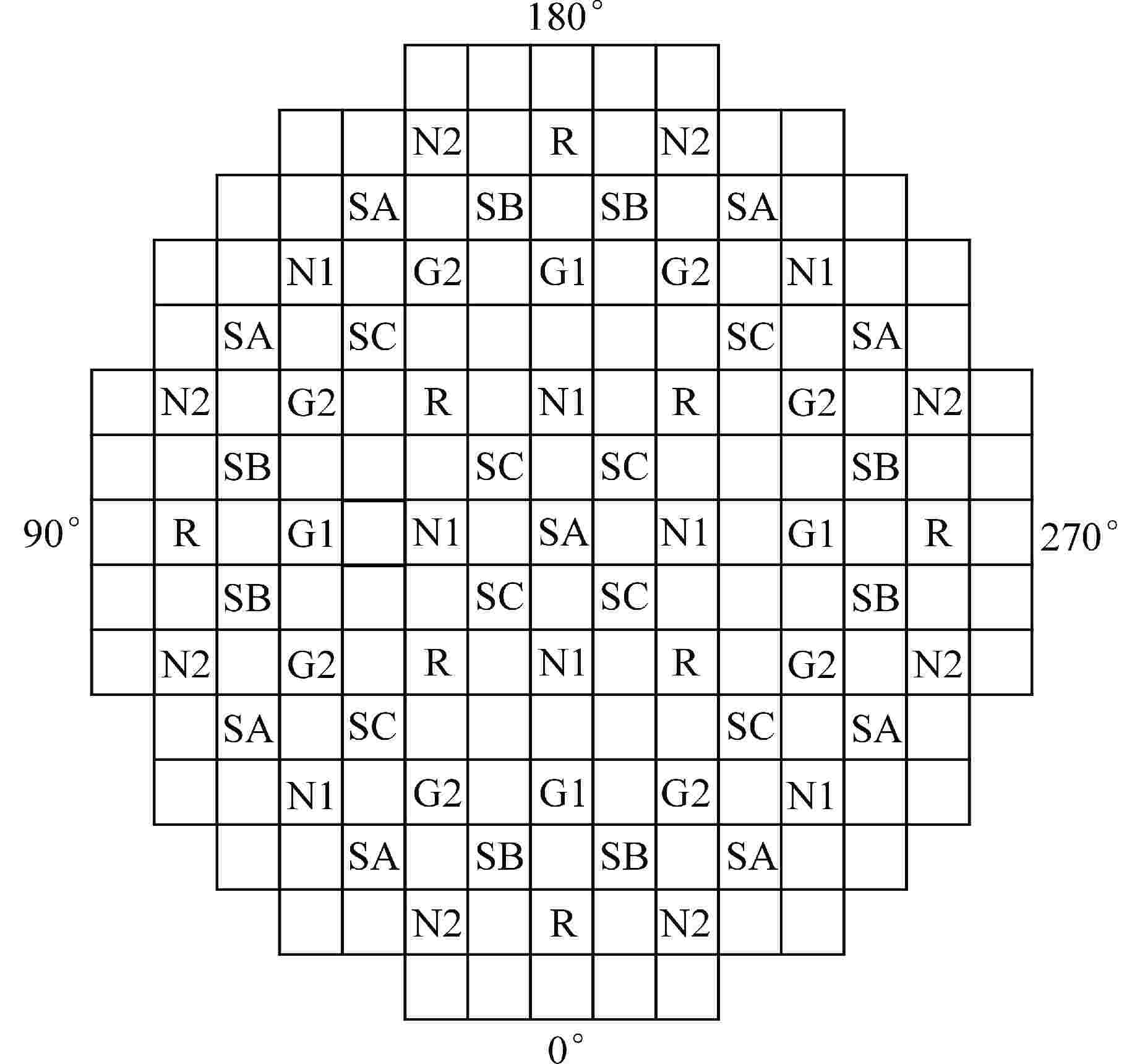
棒组 实测值/pcm SHARK/pcm 相对偏差/% 稀释法测R棒（ARO） 1213.9 1236.9 1.89 稀释法测G1棒（Rin） 403.7 404.6 0.22 稀释法测SB 1242.6 1244.1 0.12 换棒法测SA 1029.4 1055.3 2.52 换棒法测N2 950.8 977.5 2.81 换棒法测N1 889.7 903.9 1.60 换棒法测G2 843.7 847.7 0.47 换棒法测SC 777.1 791.7 1.88 换棒法测G1 450.6 445.4 −1.15
下载: 导出CSV
-
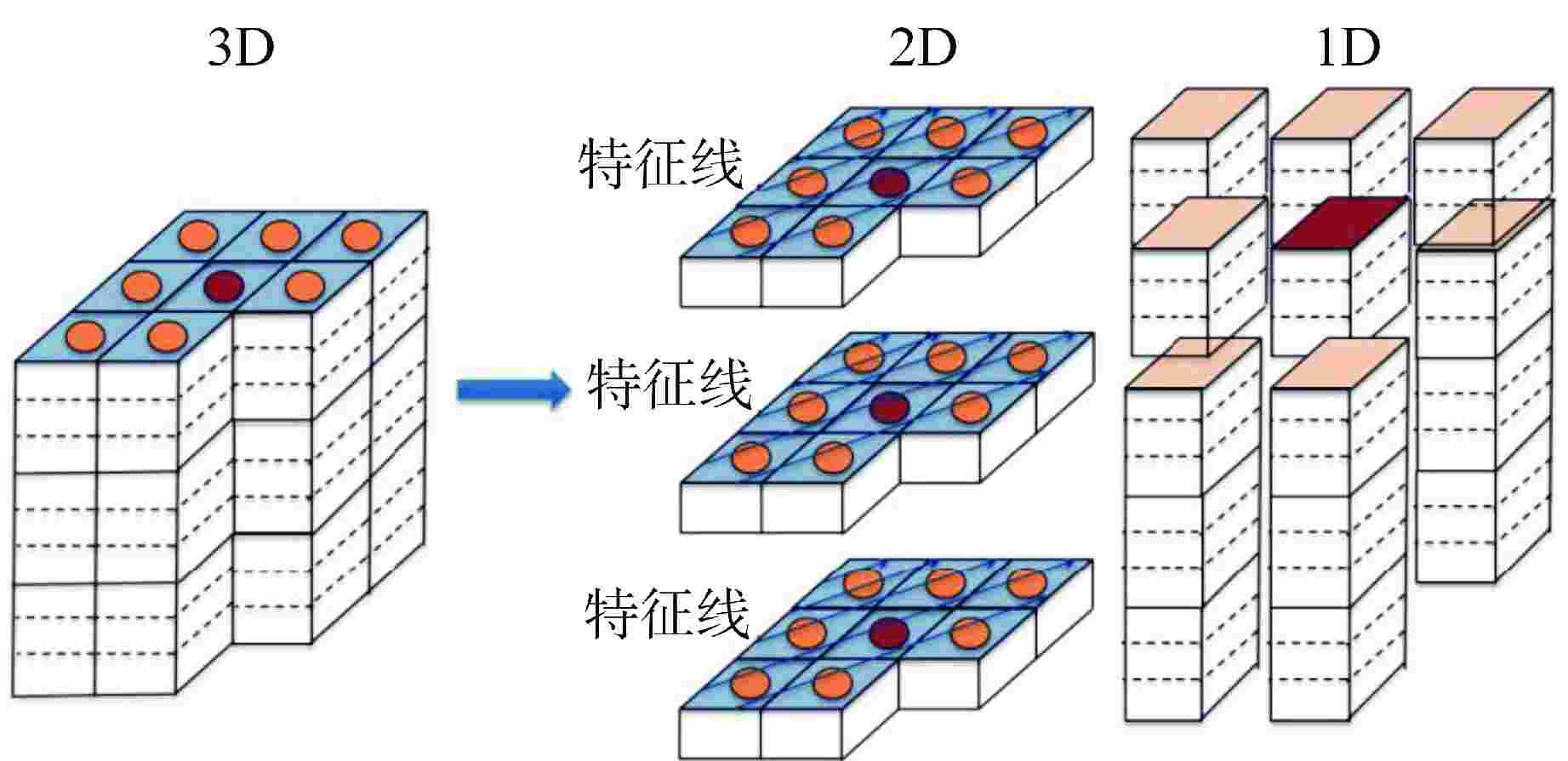
[1] 梁亮. 基于特征线方法的2D/1D及2D/3D耦合中子输运计算方法研究[D]. 西安: 西安交通大学,2017. [2] 赵晨. 二维/一维耦合特征线方法的改进及在数值反应堆物理计算中的应用[D]. 西安: 西安交通大学,2019. [3] HURSIN M. Full core, heterogeneous, time dependent neutron transport calculations with the 3D code DeCART[D]. U.S.: University of California at Berkeley, 2010. [4] JUNG Y S. Development of practical numerical nuclear reactor for high fidelity core analysis[D]. Korea: Seoul National University, 2013. [5] Choi S, Choe J, Nguyen K, et al. Recent development status of neutron transport code STREAM[C]//Transactions of the Korean Nuclear Society Spring Meeting. Jeju:Korean Nuclear Society, 2019. [6] KELLEY B W, LARSEN E W. 2D/1D approximations to the 3D neutron transport equation. I: theory[C]//2013 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering. Sun Valley: U. S. Department of Energy, 2013. [7] CHEN J, LIU Z Y, ZHAO C, et al. A new high-fidelity neutronics code NECP-X[J]. Annals of Nuclear Energy, 2018, 116: 417-428. doi: 10.1016/j.anucene.2018.02.049 [8] ZHANG H B, PENG X J, ZHAO C, et al. Subgroup method for the high fidelity neutronics code SHARK and preliminary benchmarking[J]. Nuclear Engineering and Design, 2023, 408: 112308. doi: 10.1016/j.nucengdes.2023.112308 [9] 赵晨,赵文博,张宏博,等. 基于数字化反应堆物理计算程序SHARK的一步法输运计算方法研究[J]. 核动力工程,2023, 44(4): 33-40, doi: 10.13832/j.jnpe.2023.04.0033. [10] 张知竹,廖鸿宽,李庆,等. 华龙一号LPD在线监测系统误差分析[J]. 核动力工程,2020, 41(2): 11-15. -
计量
- 文章访问数: 36
- HTML全文浏览量: 15
- PDF下载量: 22
- 被引次数: 0
