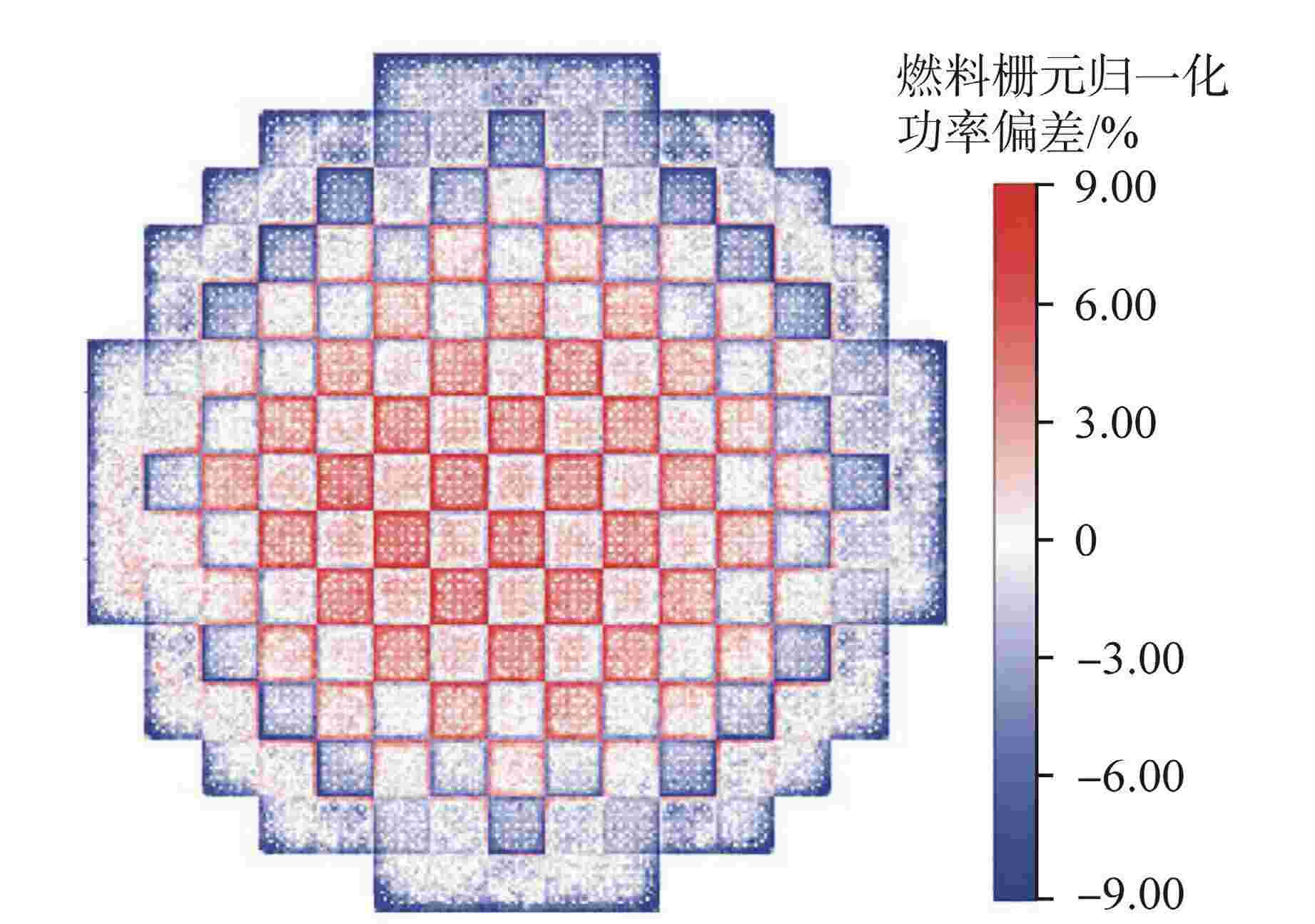
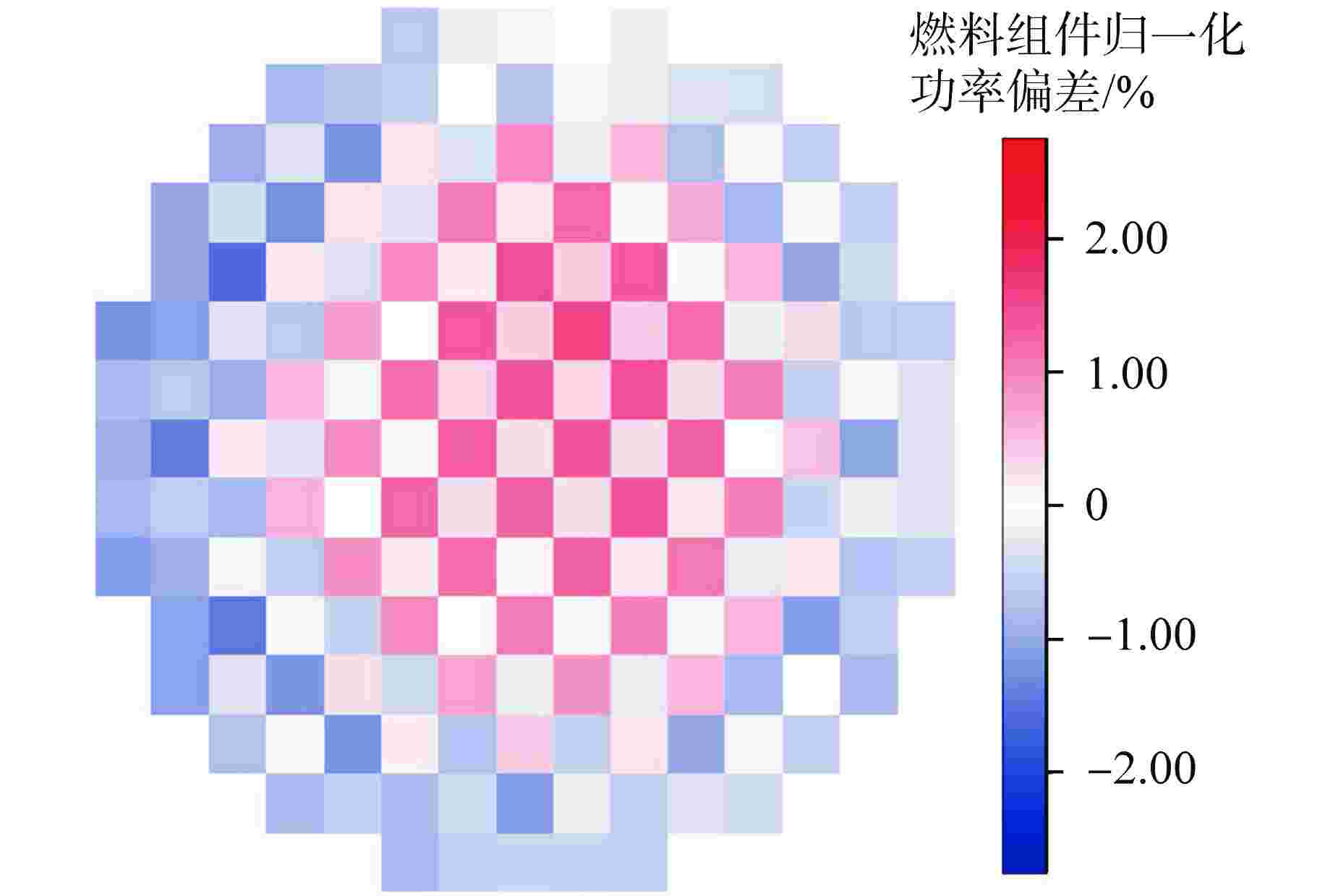
Numerical Verification of SP3 Based Computational Physics Code for Rod-type PWRs
-
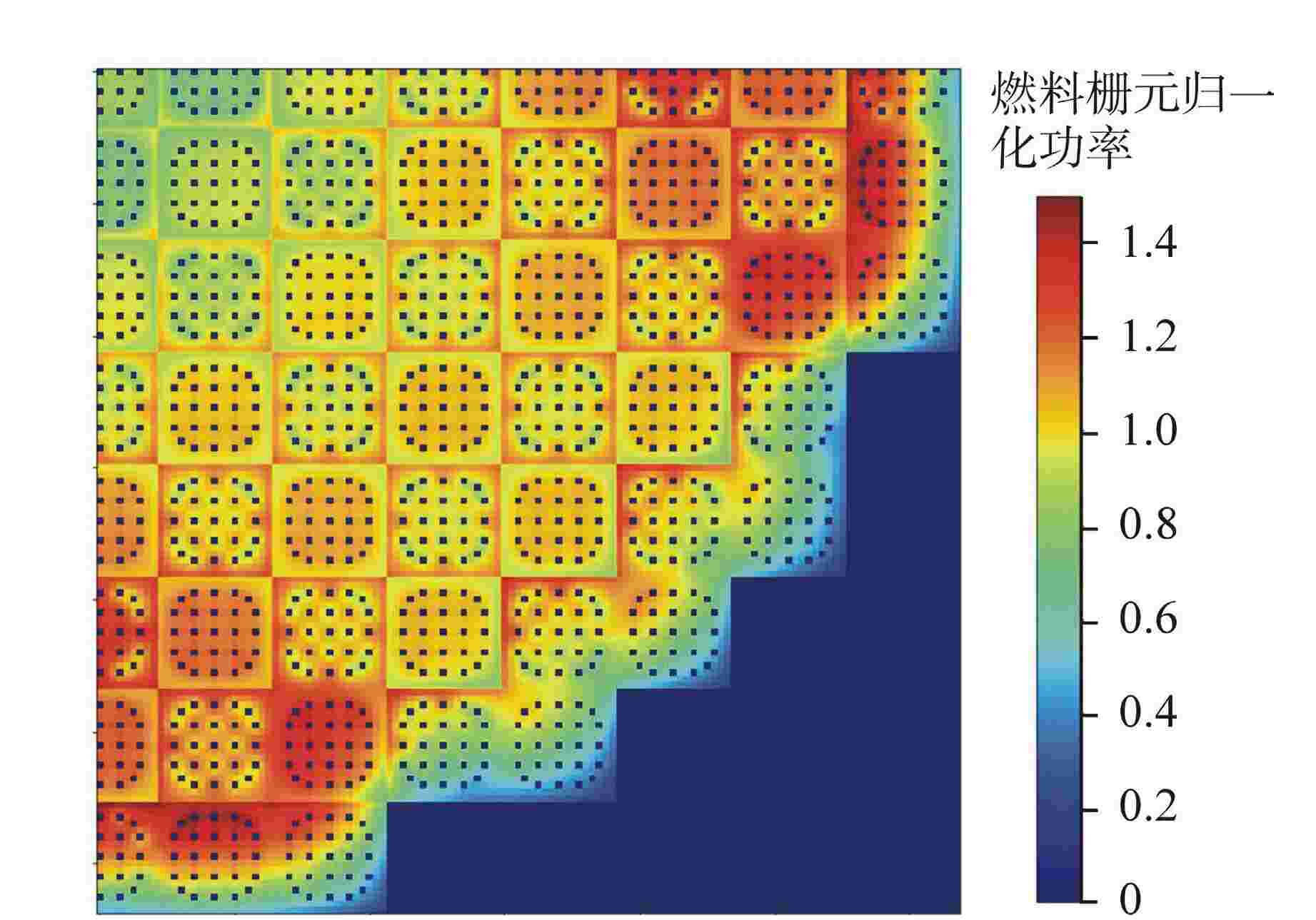
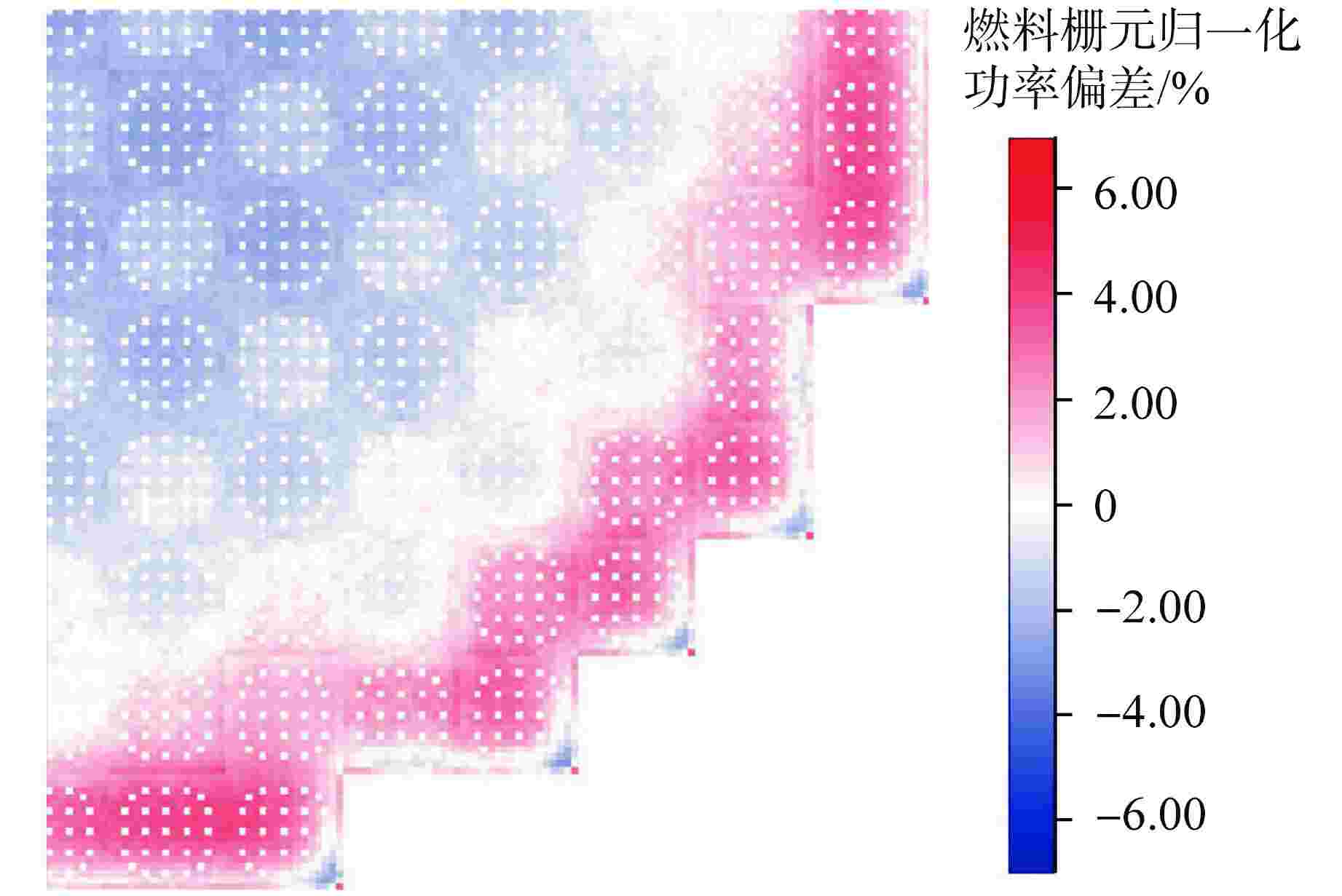
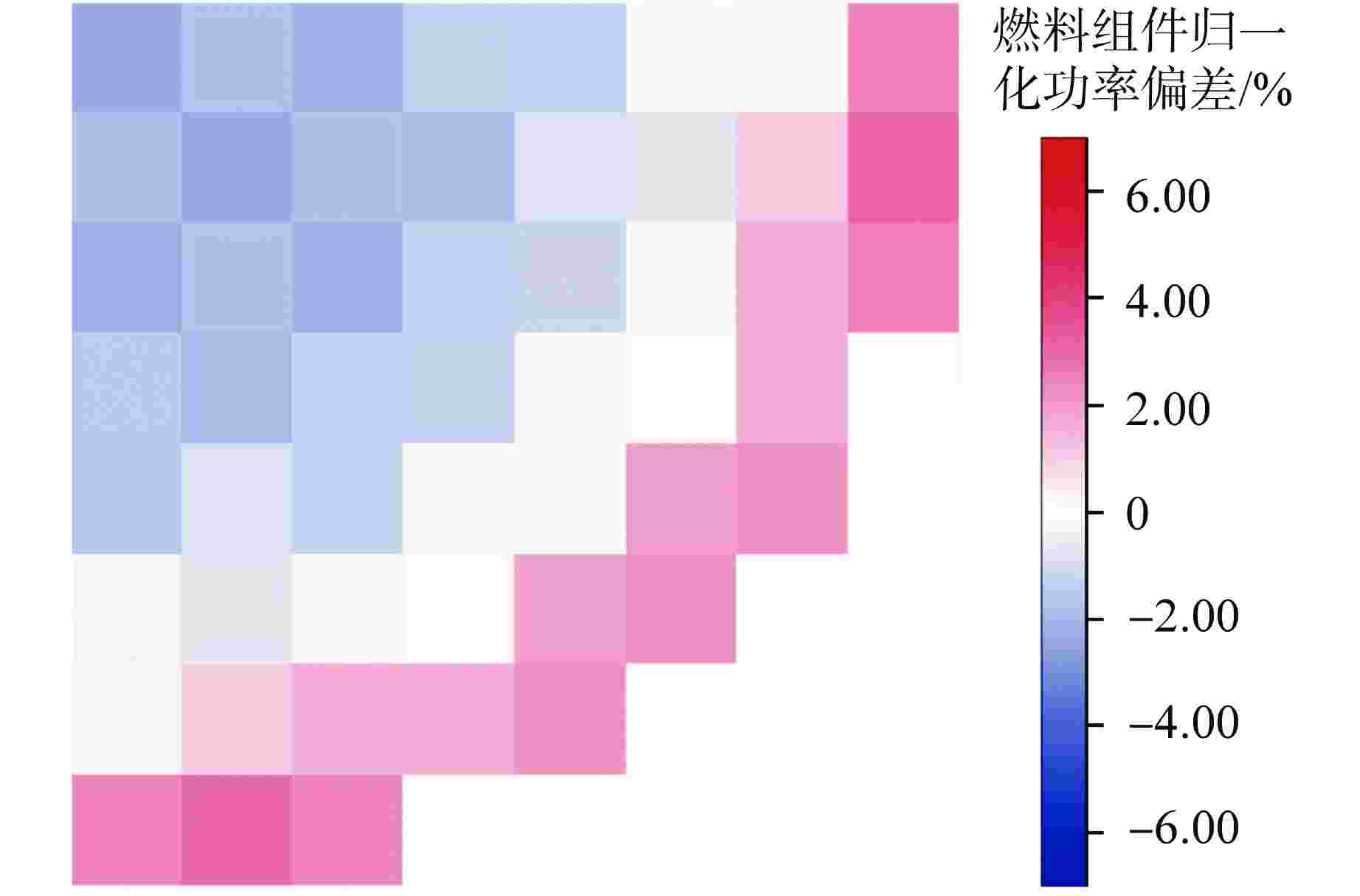
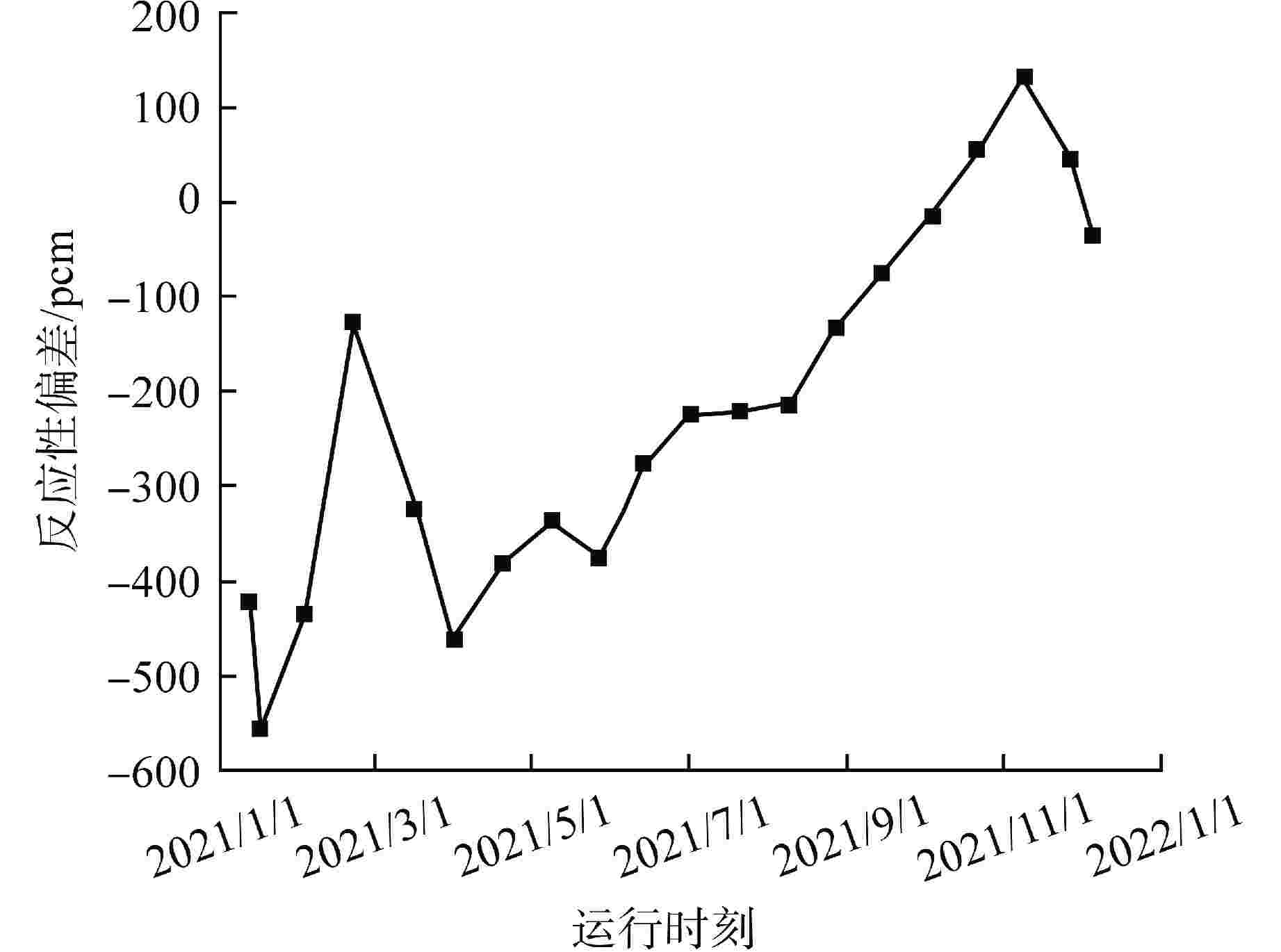
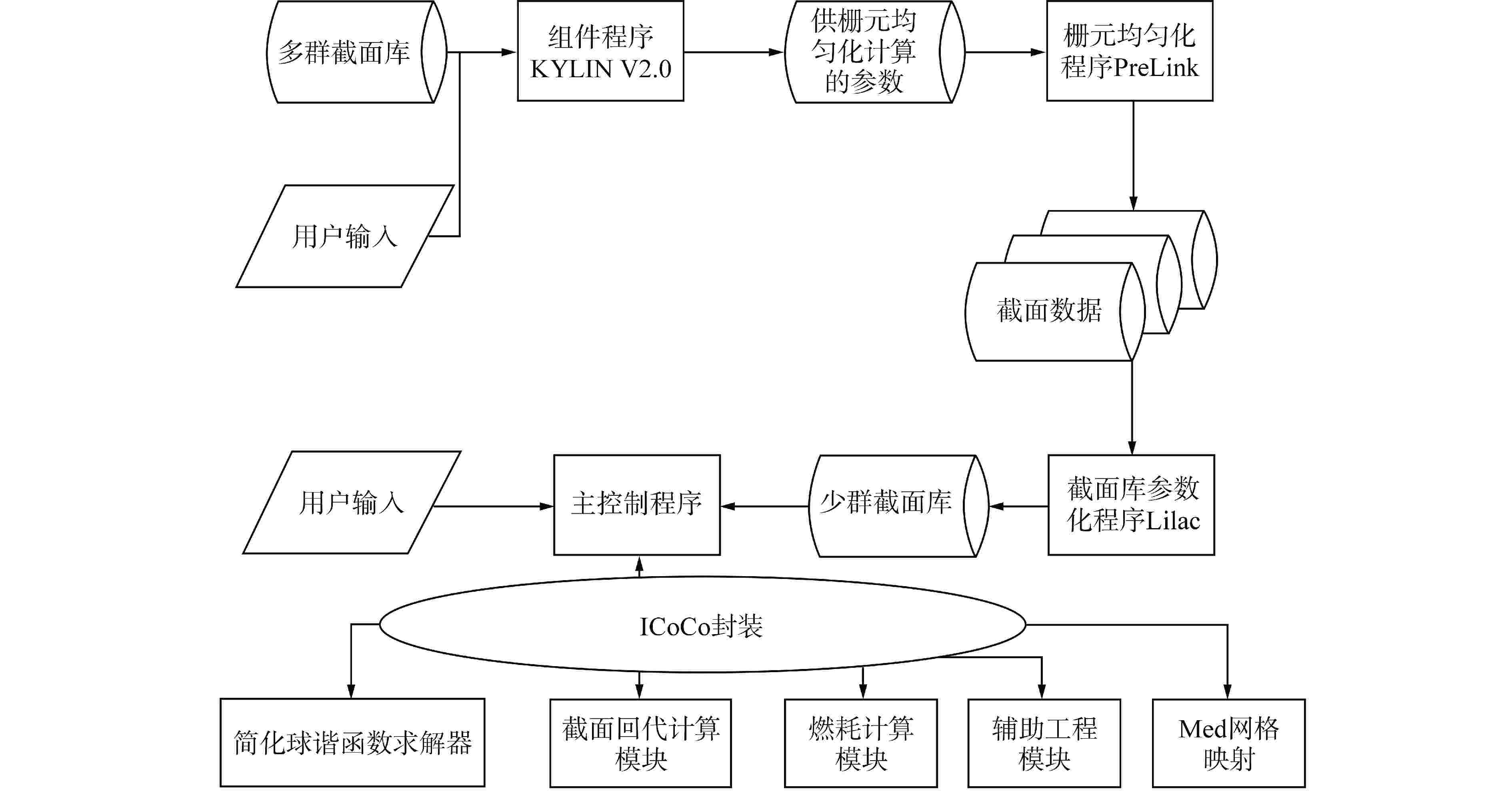
摘要: 为验证新研发程序,采用新一代的Pin-by-Pin求解程序包KYLIN V2.0-CORCA-SPn,开展了针对福清核电厂5号机组首循环实测数据的验证分析。研究结果表明,控制棒价值最大相对偏差为N2棒组,为7.17%,其余棒组相对偏差均小于5%,循环内的临界反应性误差最大为−0.559%;燃料栅元功率与堆用蒙特卡罗程序RMC的偏差在8%以内。本文提出的数值模型离散精度高、计算稳定性好,相关验证工作能够为新一代压水堆堆芯程序设计提供技术支撑,进而满足新型复杂反应堆的研发设计需求。
-
关键词:
- 简化球谐函数方法 /
- Pin-by-pin /
- 压水堆 /
- 堆芯计算 /
- 华龙一号
Abstract: In order to verify the new R&D code, a new generation of Pin-by-pin solution package KYLIN V2.0-CORCA-SPn is used to verify and analyze the measured data of the first cycle of Fuqing Unit 5. The results show that the maximum integral rod worth difference is 7.17%, which occurs in N2 rod bank, while the others are lower than 5%. The maximum critical reactivity difference in the cycle is −0.559%. The deviation between fuel pin power and RMC code is within 8%. The numerical model proposed in this paper has high discrete accuracy and good computational stability, and the relevant verification work can provide technical support for the core code design of a new generation of pressurized water reactors, thus meeting the research and development design requirements of new complex reactors.-
Key words:
- SP3 method /
- Pin-by-pin /
- PWR /
- Reactor core calculation /
- HPR1000
-
表 1 控制棒价值计算结果比较
Table 1. Comparison of Control Rod Bank Integral Worth
棒组 计算值/pcm 绝对偏差/pcm 相对偏差/% 功率补偿棒组 G1 455 4 0.94 G2 873 30 3.52 N1 876 −13 −1.49 N2 1019 68 7.17 温度调节棒组 R 1230 16 1.30 停堆棒组 SA 1071 41 4.01 SB 1258 16 1.25 SC 749 −28 −3.60 表 2 功率运行期间keff比较
Table 2. Comparison of Effective Multiple Factors During the Reactor Operation
燃耗/
[MW·d·t−1·(U)]keff/pcm 反应性偏差/pcm RMC CORCA-SPn 0 1.000076 0.99820 −188 150 0.966124 0.96715 103 500 0.965816 0.96572 −10 1000 0.967884 0.96747 −41 2000 0.968268 0.96789 −38 3000 0.965827 0.96523 −60 4000 0.962257 0.96150 −76 5000 0.958070 0.95720 −87 6000 0.953224 0.95250 −72 7000 0.947867 0.94745 −42 8000 0.942032 0.94208 5 9000 0.935736 0.93641 67 10000 0.929174 0.93049 132 11000 0.922321 0.92436 204 12000 0.915389 0.91806 267 12585 0.911194 0.91439 320 注:反应性偏差= (1/keff, RMC−1/keff, CORCA-SPn)×105 -
[1] ZHANG B C, MAYHUE L, HURIA H, et al. Development of a three-dimensional pseudo pin-by-pin calculation methodology in ANC[J]. Nuclear Technology, 2013, 183(3): 527-534. doi: 10.13182/NT13-A19439 [2] HÉBERT A. A consistent technique for the pin-by-pin homogenization of a pressurized water reactor assembly[J]. Nuclear Science and Engineering, 1993, 113(3): 227-238. doi: 10.13182/NSE92-10 [3] YAMAMOTO A, SAKAMOTO T, ENDO T. Discontinuity factors for simplified P3 theory[J]. Nuclear Science and Engineering, 2016, 183(1): 39-51. doi: 10.13182/NSE15-102 [4] TATSUMI M, YAMAMOTO A. Advanced PWR core calculation based on multi-group nodal-transport method in three-dimensional pin-by-pin geometry[J]. Journal of Nuclear Science and Technology, 2003, 40(6): 376-387. doi: 10.1080/18811248.2003.9715369 [5] Calloo A, Couyras D, Fevotte F, et al. COCAGNE: EDF New Neutronic Core Code for ANDROMEDE Calculation Chain[C]//Mathematics and Computational Methods in Nuclear Science and Engineering 2017. Jeju: ANS, 2017. [6] ZHAO W B, CHAI X M, ZHANG B, et al. A nodal method based on CMFD for pin-by-pin SP3 calculation[J]. Annals of Nuclear Energy, 2022, 167: 108849. doi: 10.1016/j.anucene.2021.108849 [7] 柴晓明. KYLIN-Ⅱ软件理论手册: NESTOR2E-400301-SC03[Z]. 成都:中国核动力研究设计院,2016. [8] 王武, 安南, 王侃. RMC软件用户手册: REAL-NPIC-2021-2-06[R]. 北京: 清华大学,2022. -





 下载:
下载: