RMC基于CAD几何输运功能的拓展开发应用

申鹏飞; 王侃; 刘召远; 梁金刚; 刘仕倡

doi:10.13832/j.jnpe.2024.S2.0055

RMC基于CAD几何输运功能的拓展开发应用

doi: 10.13832/j.jnpe.2024.S2.0055

1.
清华大学工程物理系，北京，100084
2.
清华大学核能与新能源技术研究院，北京，100084
3.
华北电力大学核科学与工程学院，北京，100096

基金项目: 国家自然科学基金（123B2085）

详细信息

作者简介:
申鹏飞（1996—），男，博士研究生，现主要从事蒙特卡罗方法研究，E-mail: spf20@mails.tsinghua.edu.cn

通讯作者:
王　侃，E-mail: wangkan@mail.tsinghua.edu.cn

中图分类号: TL329⁺.2
计量
- 文章访问数: 24
- HTML全文浏览量: 10
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2024-07-24
- 修回日期: 2024-09-11
- 刊出日期: 2025-01-06

Extended Development and Application of CAD-based Transport in RMC

1.
Department of Engineering Physics, Tsinghua University, Beijing, 100084, China
2.
Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing, 100084, China
3.
School of Nuclear Science and Engineering, North China Electric Power University, Beijing, 100096, China

摘要

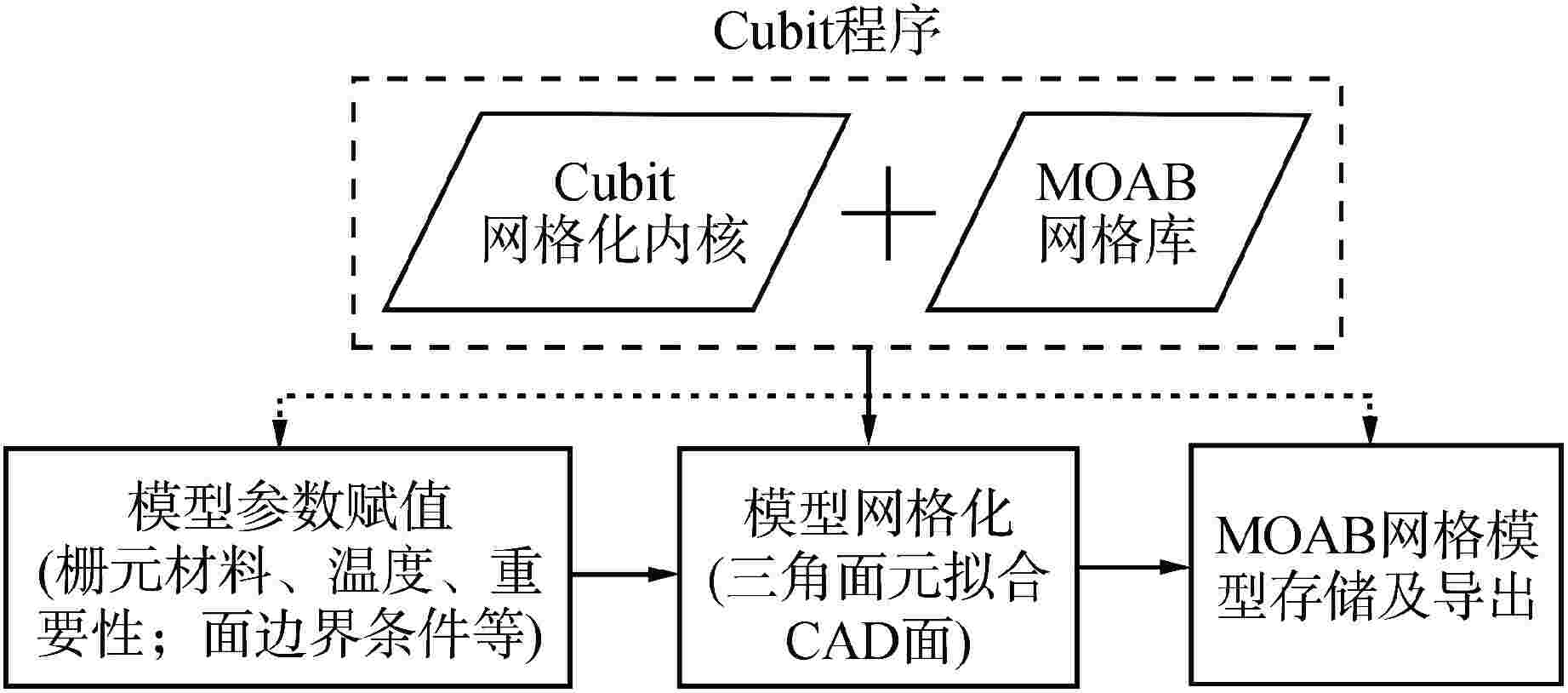
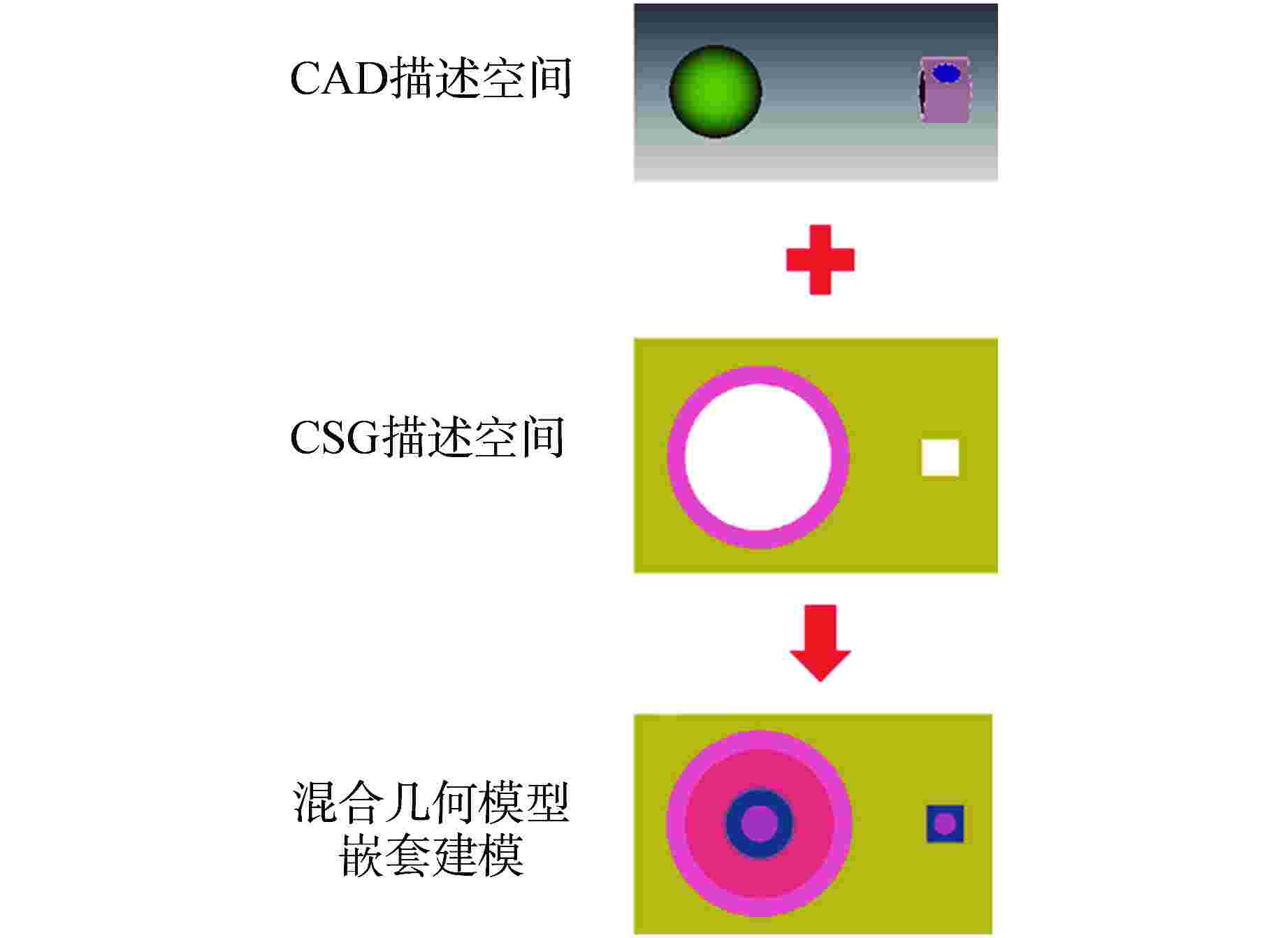
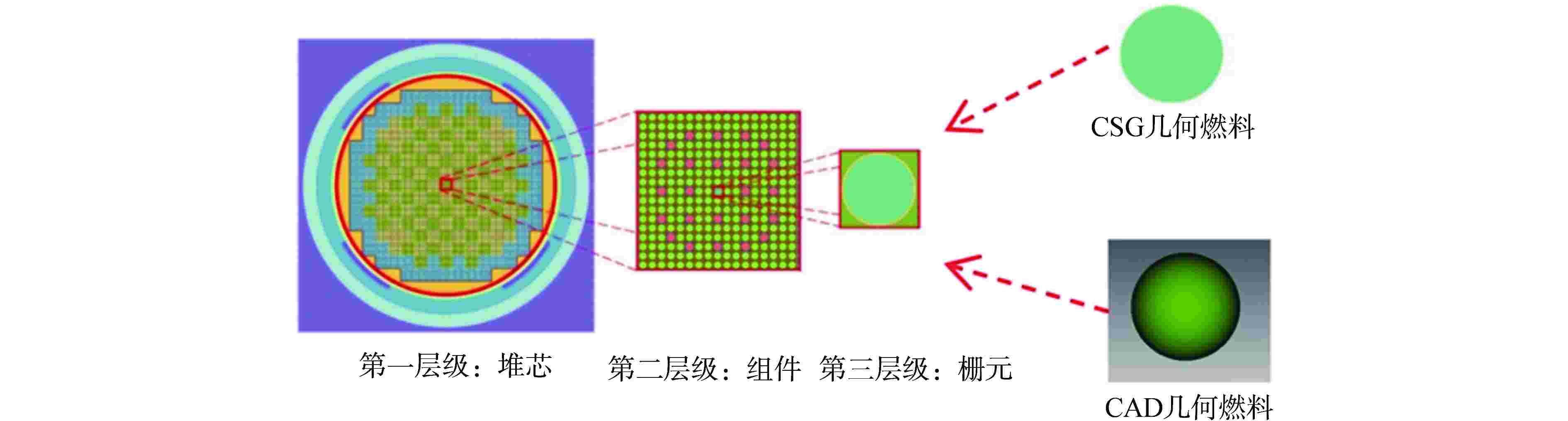
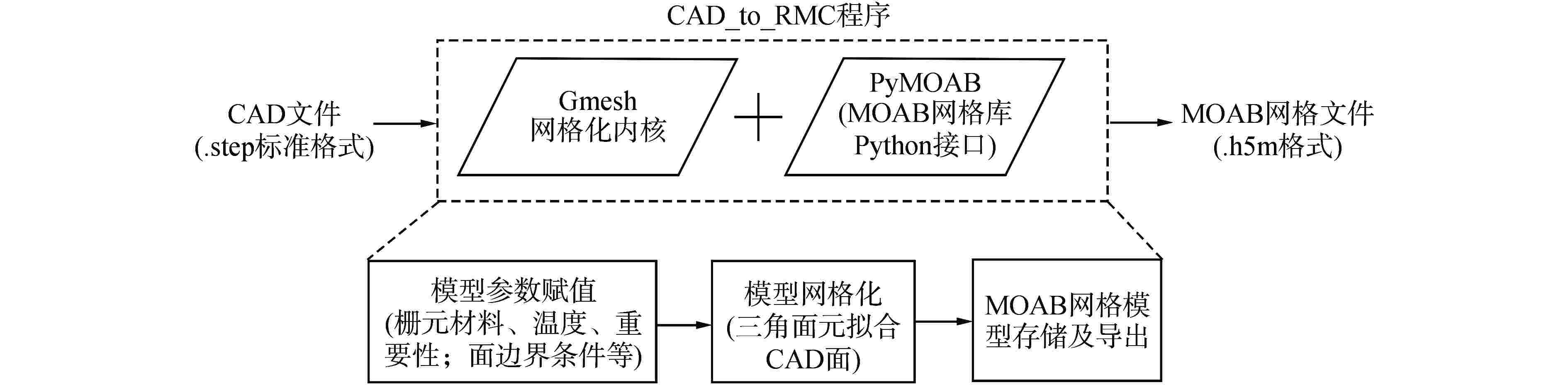
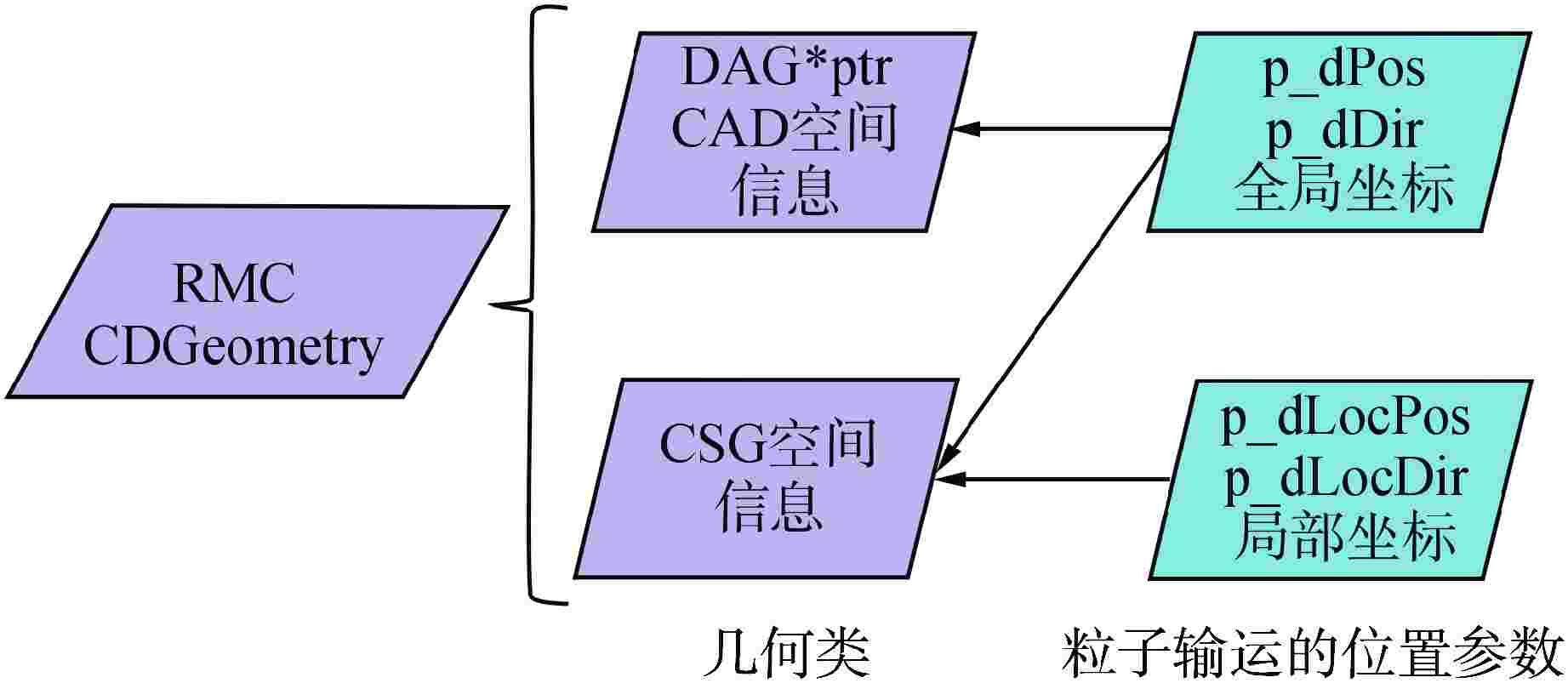
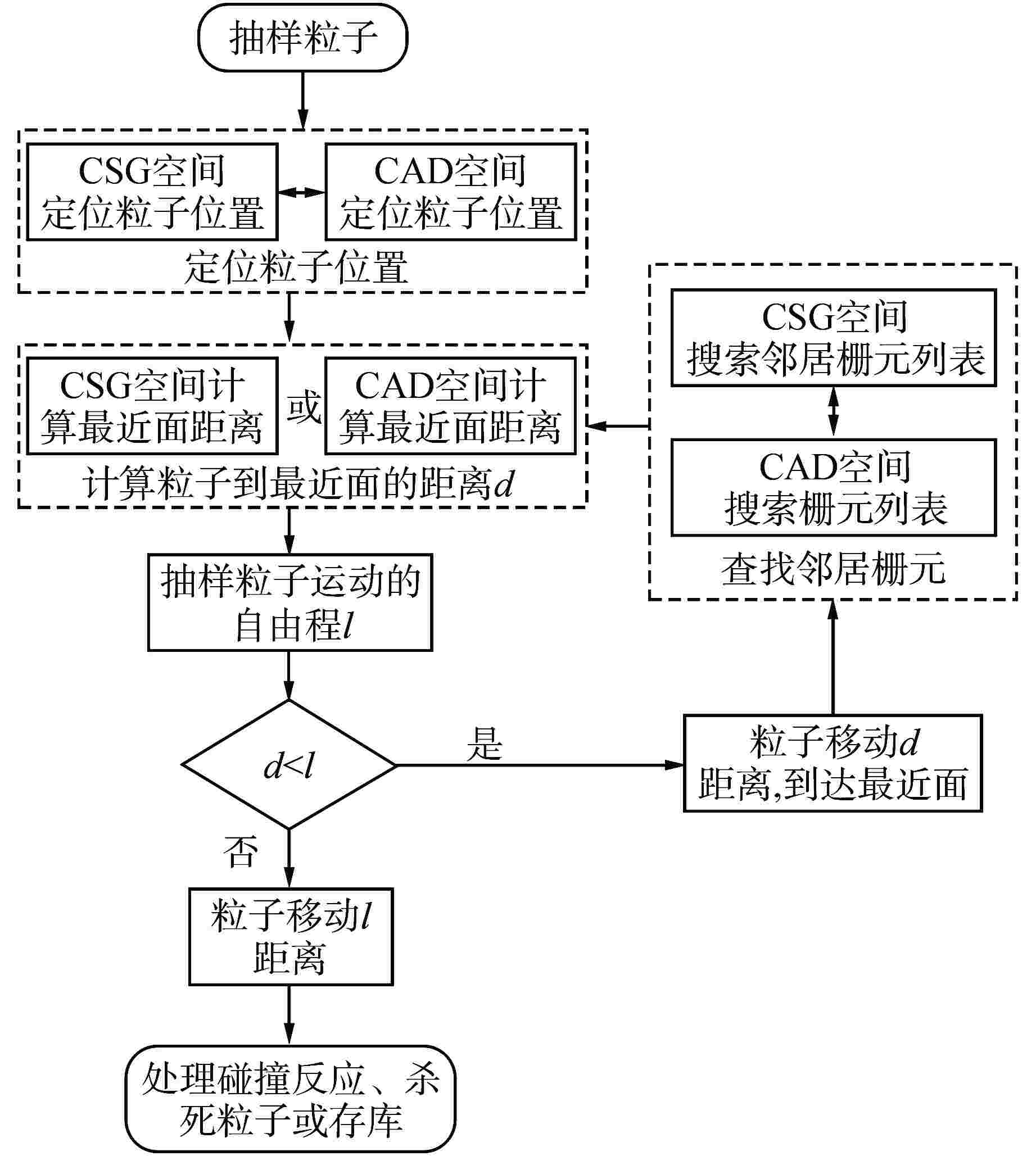
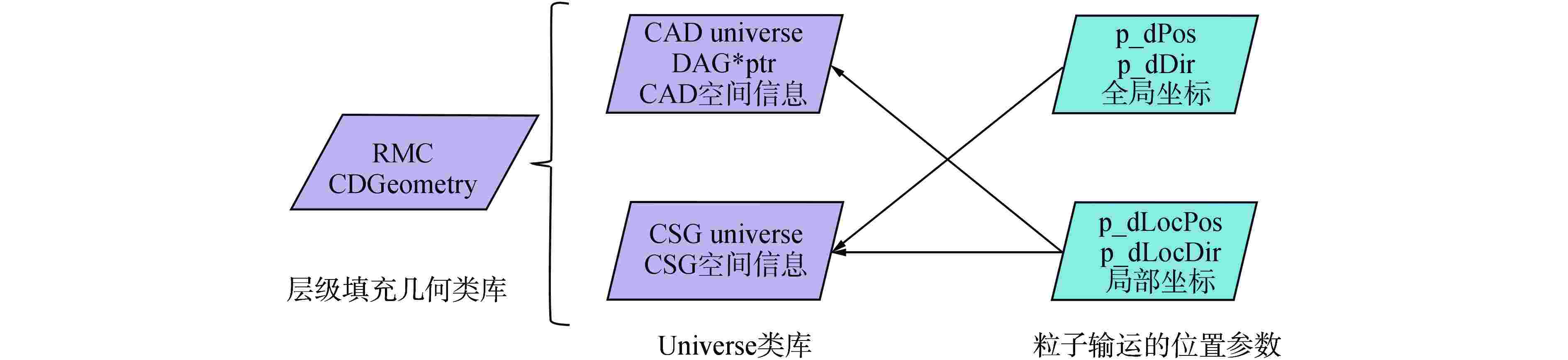
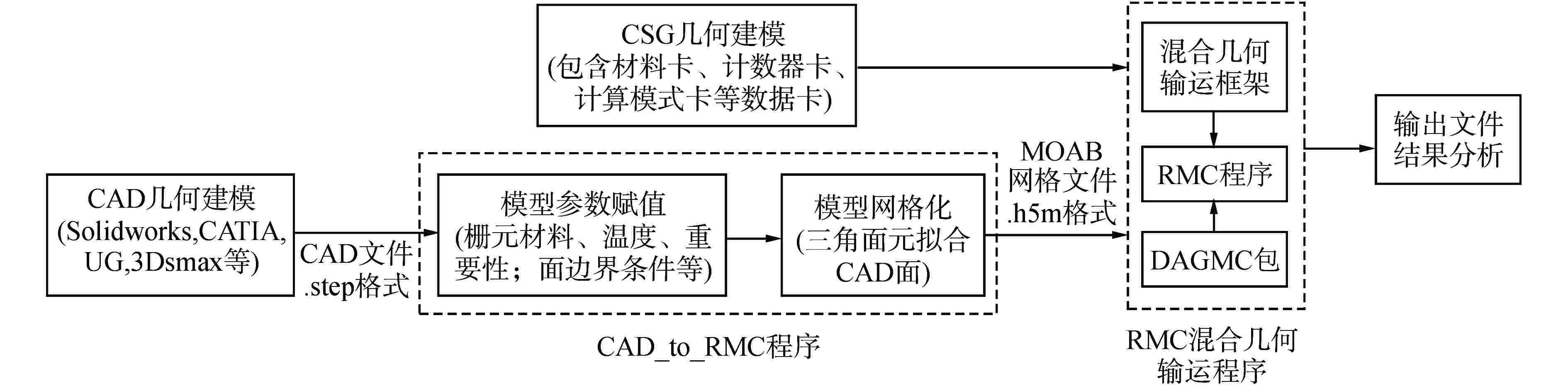
摘要: 为拓展蒙特卡罗程序RMC基于计算机辅助设计（CAD）几何输运能力，面向新型数值反应堆的RMC基于CAD几何建模输运提供新的计算手段。首先采用开源网格化内核处理CAD几何模型，实现全流程自主化的RMC基于CAD几何输运方法，其次开发了CAD与构造实体几何（CSG）的混合几何输运框架，提高几何处理效率和RMC输运效率。通过燃料球、VERA-3A燃料组件等模型的数值计算，验证了自主化CAD几何处理方法、混合几何建模输运方法的正确性；与现有CAD几何建模输运方法相比，混合几何建模输运方法在几何处理时间、计算效率等方面取得显著提升。因此，本研究开发的RMC基于CAD几何输运拓展功能可以用于新型数值反应堆的中子学分析计算。
- 构造实体几何（CSG） /
- 混合几何 /
- CAD几何 /
- RMC /
- 网格化 /
- 蒙特卡罗
Abstract: To enhance the capability of CAD-based transport in RMC, and provide a new calculation method for the CAD-based geometry transport modeling in Monte Carlo (MC) for new numerical reactors, in this study, firstly, an open-source meshing kernel is employed to process CAD models, realizing an autonomous CAD-based transport method throughout the entire process in the Monte Carlo code RMC. Subsequently, a hybrid geometric transport framework combining CAD and CSG geometry is developed, which improves the efficiency of geometric processing and Monte Carlo transport. The correctness of the autonomous CAD geometric processing method and the hybrid geometric transport method is verified through numerical calculations of fuel spheres, VERA-3A fuel assembly and other models. Compared with the existing CAD geometric modeling transportation methods, the hybrid geometric modeling transportation method has significantly improved the geometric processing time and the efficiency of Monte Carlo calculation. Therefore, the enhanced CAD-based transport method in RMC developed in this study can be used for neutron transport analysis calculations of new numerical reactors.
- Constructive solid geometry (CSG) /
- Hybrid geometry /
- CAD geometry /
- RMC /
- Geometry meshing /
- Monte Carlo

HTML全文

图 1 RMC基于CAD几何输运的计算流程

Figure 1. Workflow of CAD-based Transport in RMC

下载: 全尺寸图片幻灯片

图 2 Cubit软件处理CAD模型流程图

Figure 2. Workflow of Processing CAD Models in Cubit Software

下载: 全尺寸图片幻灯片

图 3 混合几何嵌套建模方式

Figure 3. Nested Modeling Scheme of Hybrid Geometry

下载: 全尺寸图片幻灯片

图 4 混合几何层级填充建模方式

Figure 4. Layered Modeling Scheme of Hybrid Geometry

下载: 全尺寸图片幻灯片

图 5 CAD_to_RMC程序处理流程

Figure 5. Workflow of CAD_to_RMC Code

下载: 全尺寸图片幻灯片

图 6 嵌套输运框架类库设计

Figure 6. Class Structure of Nested Transport Scheme

下载: 全尺寸图片幻灯片

图 7 嵌套输运框架输运流程

Figure 7. Ray-tracking Process of Nested Transport Scheme

下载: 全尺寸图片幻灯片

图 8 层级填充输运框架类库设计

Figure 8. Class Structure of Layered Transport Scheme

下载: 全尺寸图片幻灯片

图 9 RMC基于混合几何输运的计算流程

Figure 9. Workflow of Hybrid Geometry Transport in RMC

下载: 全尺寸图片幻灯片

图 10 燃料球、燃料短棒模型示意图

Figure 10. Schematic Diagram of Fuel Sphere and Pin Model

下载: 全尺寸图片幻灯片

图 11 燃料球块嵌套几何模型示意图

Figure 11. Nested Geometry of Fuel Sphere and Pin Model

下载: 全尺寸图片幻灯片

图 12 VERA-3A燃料组件模型几何结构示意图

Figure 12. Geometry of VERA-3A Assembly Model

下载: 全尺寸图片幻灯片

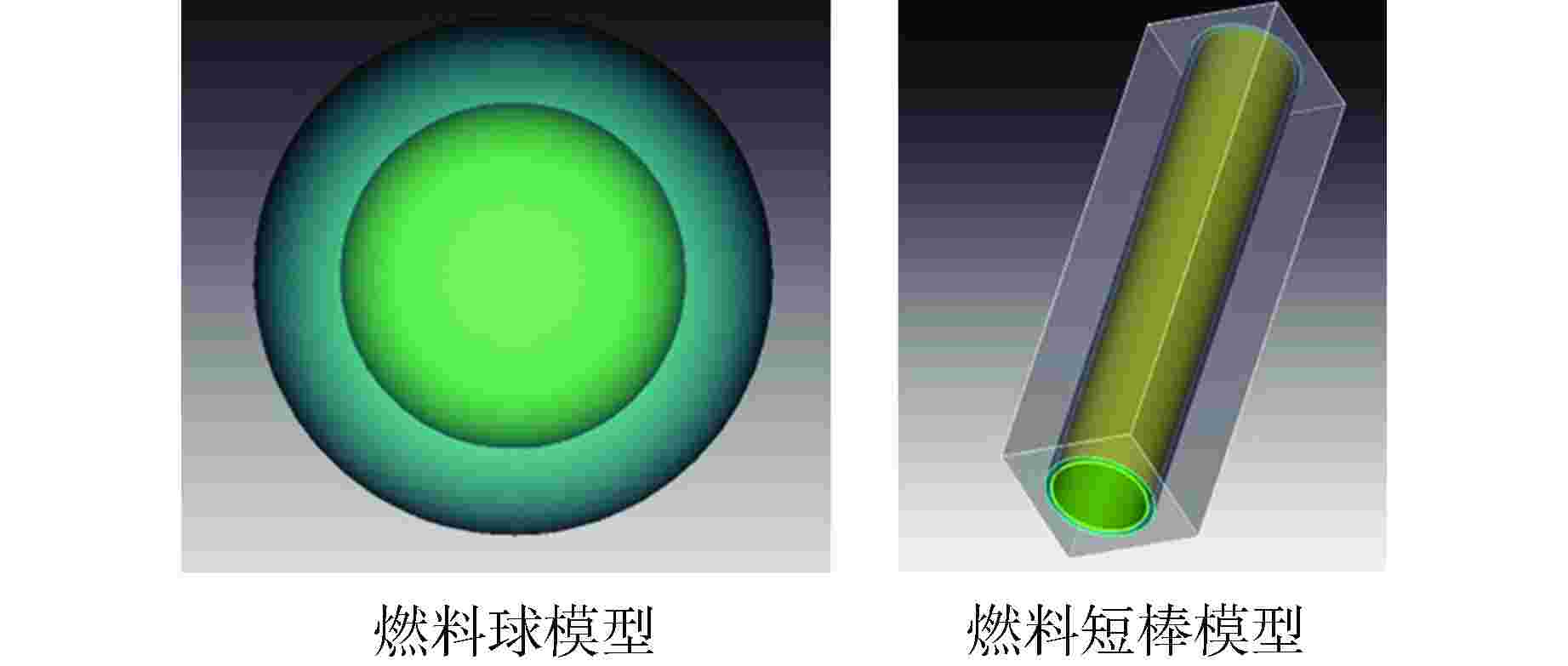
表 1 燃料球模型计算结果对比

Table 1. Calcultaion Results of Fuel Sphere Model

程序	建模方式	有效增殖系数（k_eff）	σ	偏差/σ	粒子平均碰撞数	计算耗时/min
RMC	CSG几何	0.578047	0.000805		13.97	0.099
	CAD几何（Cubit）	0.577595	0.000789	−0.69	14.07	15.35
	CAD几何（Cad_to_RMC)	0.578417	0.000821	0.56	14.03	18.90
OpenMC	CAD几何（Cubit）	0.57668	0.00081	−2.05		13.98
OpenMC	CAD几何（Cad_to_OpenMC)	0.57777	0.00081	−0.42		15.21

下载: 导出CSV

表 2 燃料短棒模型计算结果对比

Table 2. Calcultaion Results of Fuel Pin Model

参数		RMC （CSG几何）		RMC [CAD几何(Cubit)]			RMC [CAD几何(Cad_to_RMC)]
参数		计算结果	σ	计算结果	σ	偏差/σ	计算结果	σ	偏差/σ
中子通量密度/(cm⁻²·s⁻¹)	燃料芯块	5.27×10⁻¹	2.73×10⁻³	5.22×10⁻¹	2.58×10⁻³	−2.34	5.27×10⁻¹	2.54×10⁻³	0.28
	气隙	1.42×10⁻²	2.83×10⁻³	1.42×10⁻²	2.93×10⁻³	−0.38	1.42×10⁻²	2.68×10⁻³	0.83
	包壳	9.29×10⁻²	2.64×10⁻³	9.26×10⁻²	2.73×10⁻³	−0.97	9.34×10⁻²	2.50×10⁻³	1.22
	水层	3.25×10⁻¹	1.77×10⁻³	3.24×10⁻¹	1.82×10⁻³	−1.71	3.27×10⁻¹	1.51×10⁻³	2.70
计算耗时/min		0.199		2.470			5.700

下载: 导出CSV

表 3 燃料球块模型计算结果对比

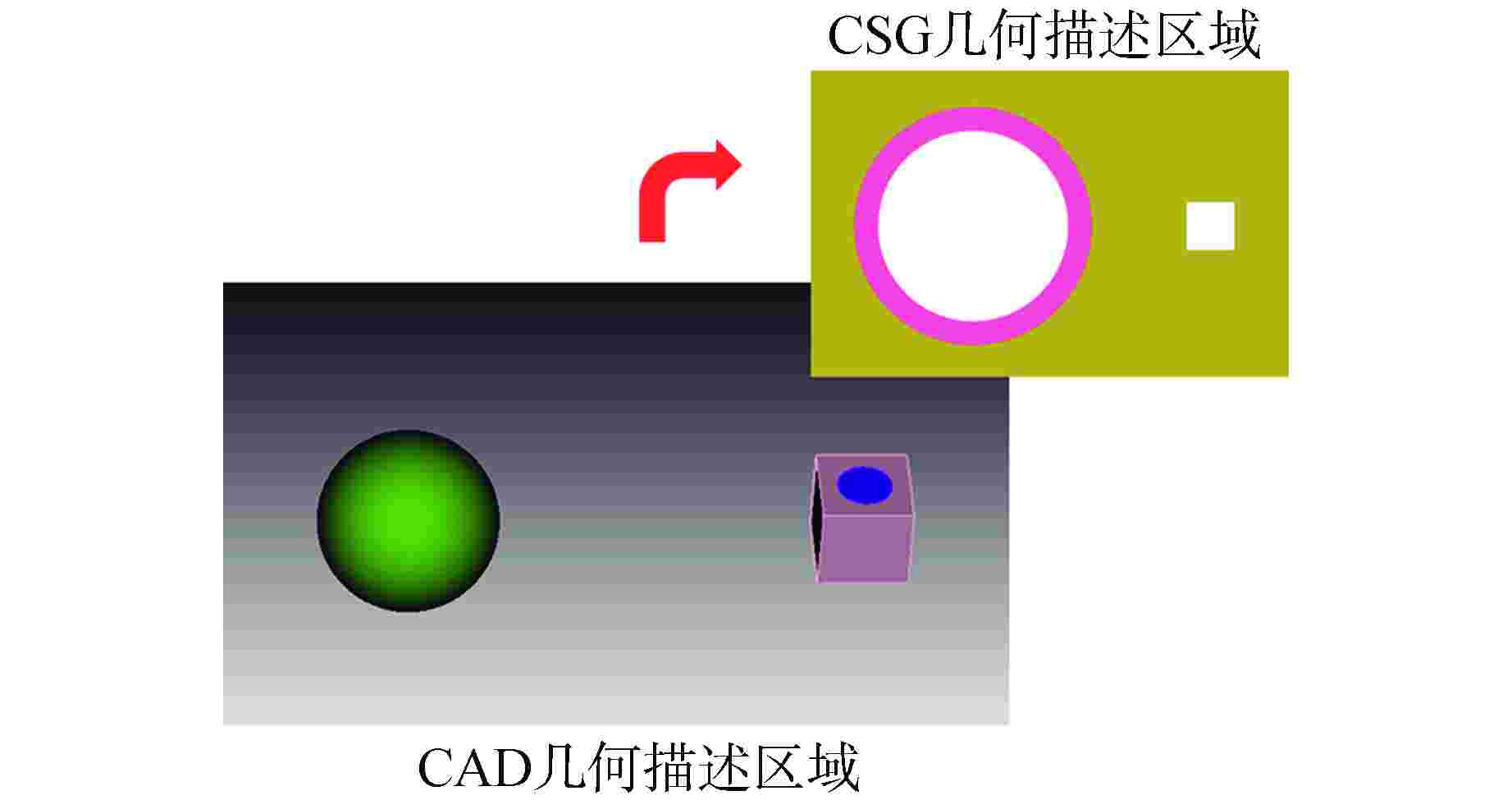
Table 3. Calcultaion Results of Fuel Sphere and Pin Model

参数		RMC（CSG几何模型）		RMC（CAD几何模型）		RMC（混合几何嵌套模型）
参数		计算结果	σ	计算结果	σ	计算结果	σ
k_eff		0.324823	0.000380	0.32466	0.000393	0.32466	0.000393
中子通量密度/(cm⁻²·s⁻¹)	燃料球芯块	3.52×10⁻³	7.50×10⁻²	3.39×10⁻³	7.49×10⁻²	3.49×10⁻³	7.53×10⁻²
	燃料球气隙	1.04×10⁻²	5.79×10⁻²	1.01×10⁻²	6.17×10⁻²	1.01×10⁻²	6.47×10⁻²
	燃料球水层	2.93×10⁻³	5.28×10⁻²	2.77×10⁻³	5.47×10⁻²	2.67×10⁻³	5.77×10⁻²
	燃料块内部	4.63×10⁻²	1.03×10⁻²	4.60×10⁻²	1.05×10⁻²	4.54×10⁻²	1.12×10⁻²
	燃料块水层	1.05×10³	5.91×10⁻⁴	1.06×10³	5.90×10⁻⁴	1.06×10³	5.93×10⁻⁴
粒子碰撞次数		1474.38		1474.59		1474.90
计算耗时/s		327		15430		7330

下载: 导出CSV

表 4 VERA-3A燃料组件模型计算结果对比

Table 4. Calcultaion Results of VERA-3A Assembly Model

参数	RMC （CSG几何模型）		RMC （CAD几何模型）		RMC （混合几何层级填充模型）
参数	计算结果	σ	计算结果	σ	计算结果	σ
k_eff	1.177635	0.000822	1.176401	0.000852	1.175728	0.000834
粒子碰撞次数	34.12		34.11		34.11
计算耗时/s	1.38×10²		1.70×10⁴		7.36×10³

下载: 导出CSV

表 5 VERA-3A燃料组件模型重点参数对比

Table 5. Key Parameters of VERA-3A Assembly Model

程序	建模方式	CAD几何文件读入耗时/s	最大单核内存占用/MB	MOAB网格文件导出时间/s
RMC	CAD几何模型	~40	~530
RMC	混合几何模型	~3	~500
CAD_to_RMC	CAD几何模型		~1000	~15
CAD_to_RMC	混合几何模型		~490	~1

下载: 导出CSV

参考文献(15)

[1]	WILSON P P H, TAUTGES T J, KRAFTCHECK J A, et al. Acceleration techniques for the direct use of CAD-based geometry in fusion neutronics analysis[J]. Fusion Engineering and Design, 2010, 85(10-12): 1759-1765. doi: 10.1016/j.fusengdes.2010.05.030
[2]	DAVIS A, BARZILLA J, FERRARI A, et al. FluDAG: a CAD based tool for high energy physics[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2019, 915: 65-74.
[3]	SHEN P F, LIANG J G, LIU S C, et al. Implementation and verification of the DAGMC module in Monte Carlo code RMC[C]//Proceedings of the 29th International Conference on Nuclear Engineering, Shenzhen: 2022.
[4]	SHRIWISE P C, ZHANG X K, DAVIS A. DAG-OpenMC: CAD-based geometry in OpenMC[J]. Transactions of the American Nuclear Society, 2020, 122(1): 395-398.
[5]	HAN M C, KIM C H, JEONG J H, et al. DagSolid: a new Geant4 solid class for fast simulation in polygon-mesh geometry[J]. Physics in Medicine & Biology, 2013, 58(13): 4595-4609.
[6]	MARTZ R L. The MCNP6 book on unstructured mesh geometry: user's guide for MCNP 6.2. 1: LA-UR-18-27630[R]. Los Alamos: Los Alamos National Laboratory, 2018.
[7]	SHU H L, CAO L Z, HE Q M, et al. Study on unstructured mesh-based Monte Carlo/deterministic coupled particle transport calculation method[J]. Nuclear Science and Engineering, 2024, 198(11): 2209-2229. doi: 10.1080/00295639.2023.2295065
[8]	LEPPÄNEN J. CAD-based geometry type in serpent 2 - application in fusion neutronics[C]//Proceedings of the Mathematics and Computation, Supercomputing in Nuclear Applications and Monte Carlo International Conference. Nashville: Curran Associates Inc. , 2015: 19-23.
[9]	SHRIWISE P. DAGMC CAD-based geometry as universes[EB/OL]. (2021-04-28)[2024-07-10]. https://github.com/openmc-dev/openmc/pull/1825.
[10]	LEPPÄNEN J. Methodology, applications and performance of the CAD-based geometry type in the serpent 2 Monte Carlo code[J]. Annals of Nuclear Energy, 2022, 176: 109259. doi: 10.1016/j.anucene.2022.109259
[11]	BIONDO E, DAVIDSON G, ADE B. Layered CAD/CSG geometry for spatially complex radiation transport scenarios[J]. Annals of Nuclear Energy, 2023, 181: 109569. doi: 10.1016/j.anucene.2022.109569
[12]	WANG K, LI Z G, SHE D, et al. RMC – a Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82: 121-129. doi: 10.1016/j.anucene.2014.08.048
[13]	TAUTGES T J, ERNST C, STIMPSON C, et al. MOAB: a mesh-oriented database[R]. Livermore, California, USA: Sandia National Laboratories, 2004.
[14]	GEUZAINE C, REMACLE J F. Gmsh: a 3-D finite element mesh generator with built-in pre- and post-processing facilities[J]. International Journal for Numerical Methods in Engineering, 2009, 79(11): 1309-1331. doi: 10.1002/nme.2579
[15]	GODFREY A T. Vera core physics benchmark progression problem specifications, revision 4: CASL-U-2012-0131-004[R]. Pittsburgh, Pennsylvania, United States: Westinghouse Electric Corporation, 2014.