Optimization Design of Grooved Sodium Heat Pipe Based on NSGA Algorithm
-
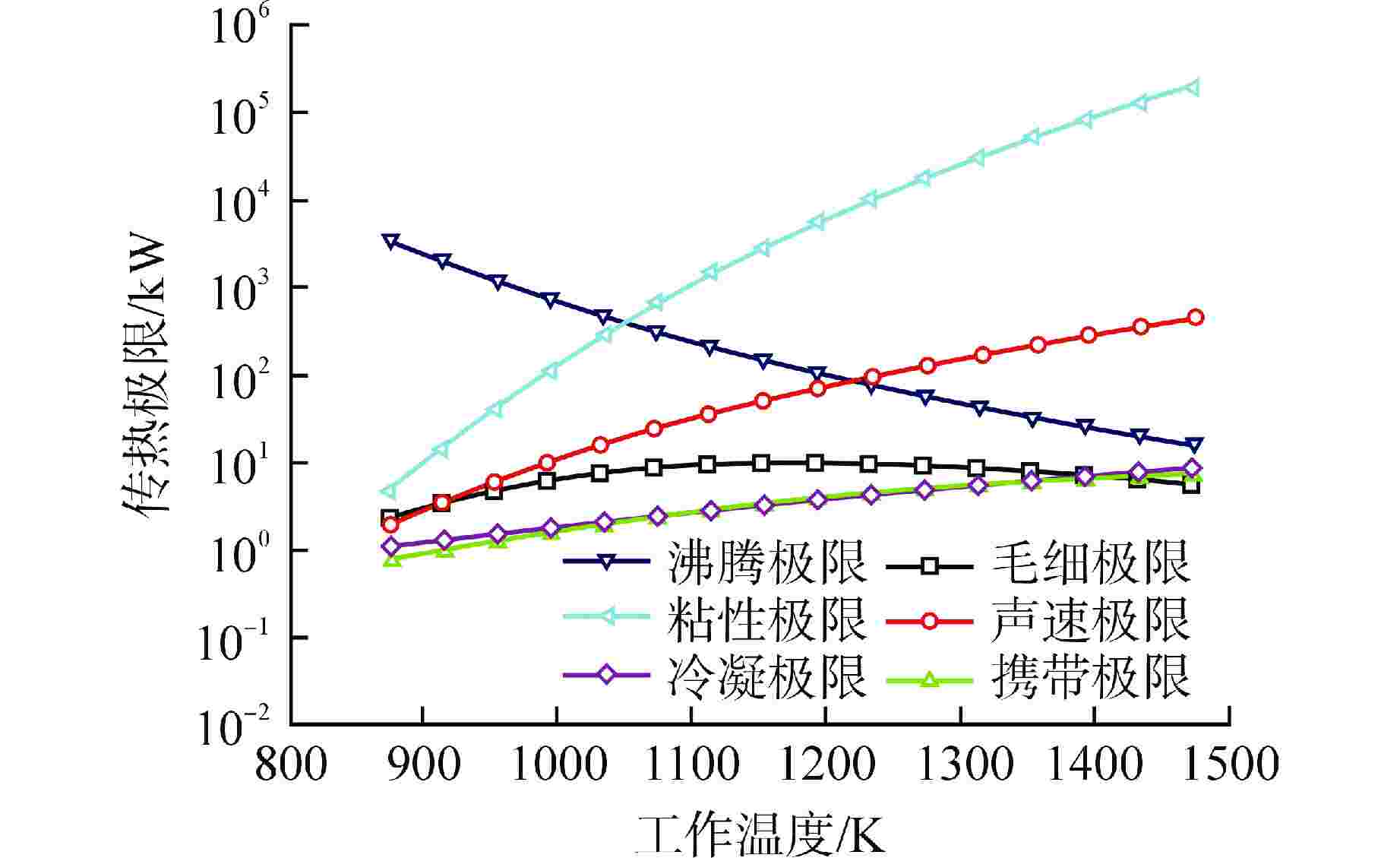
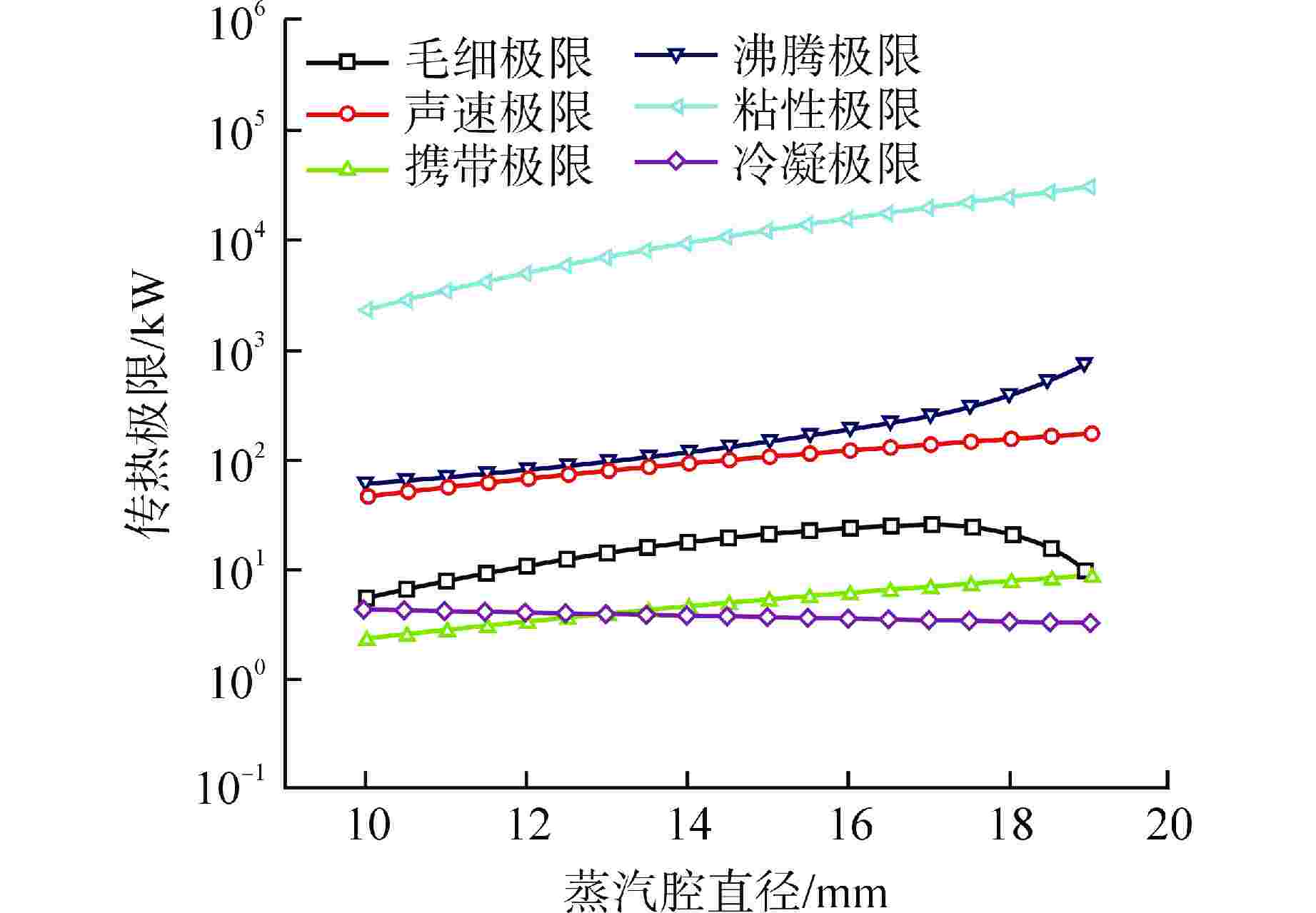
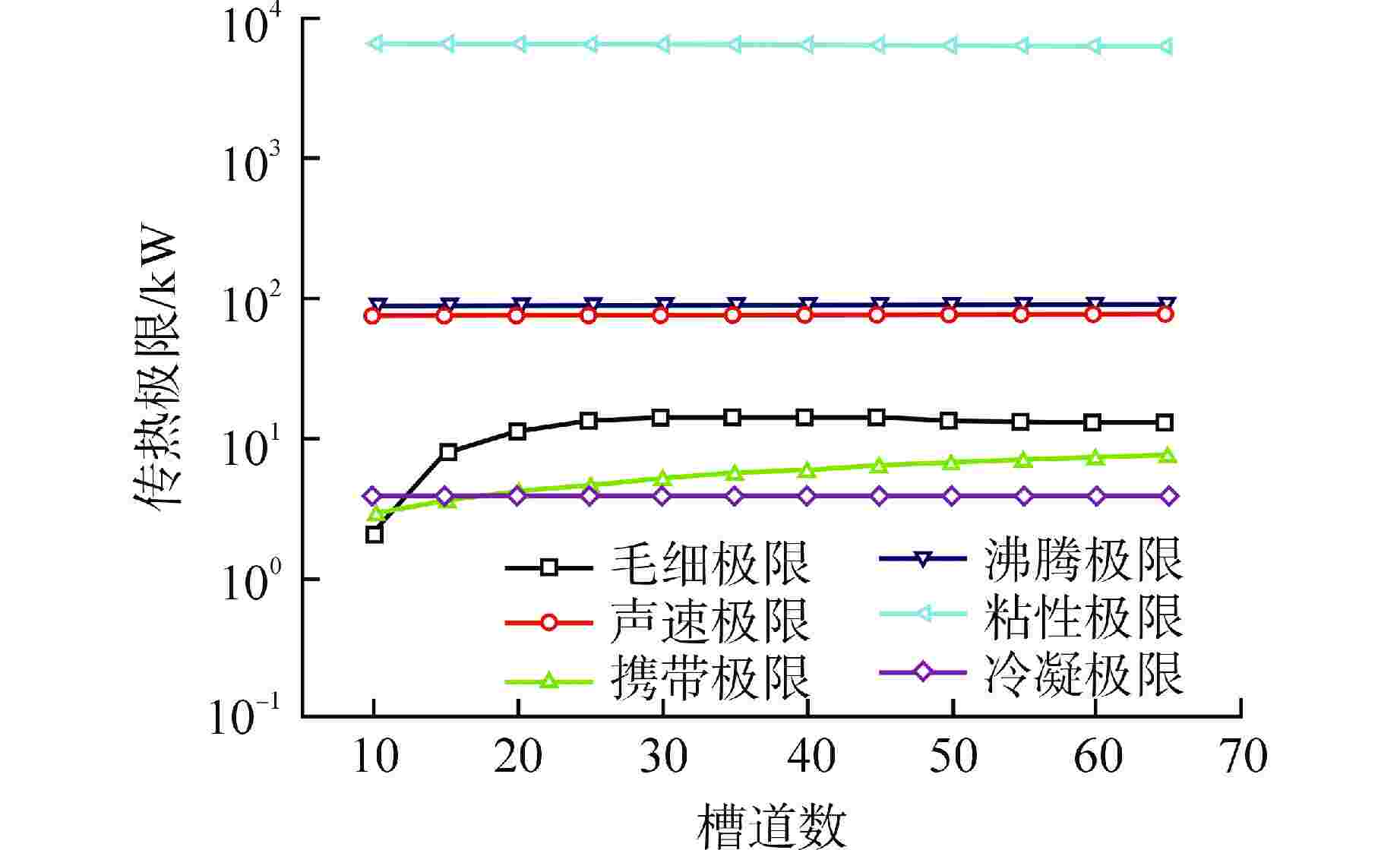
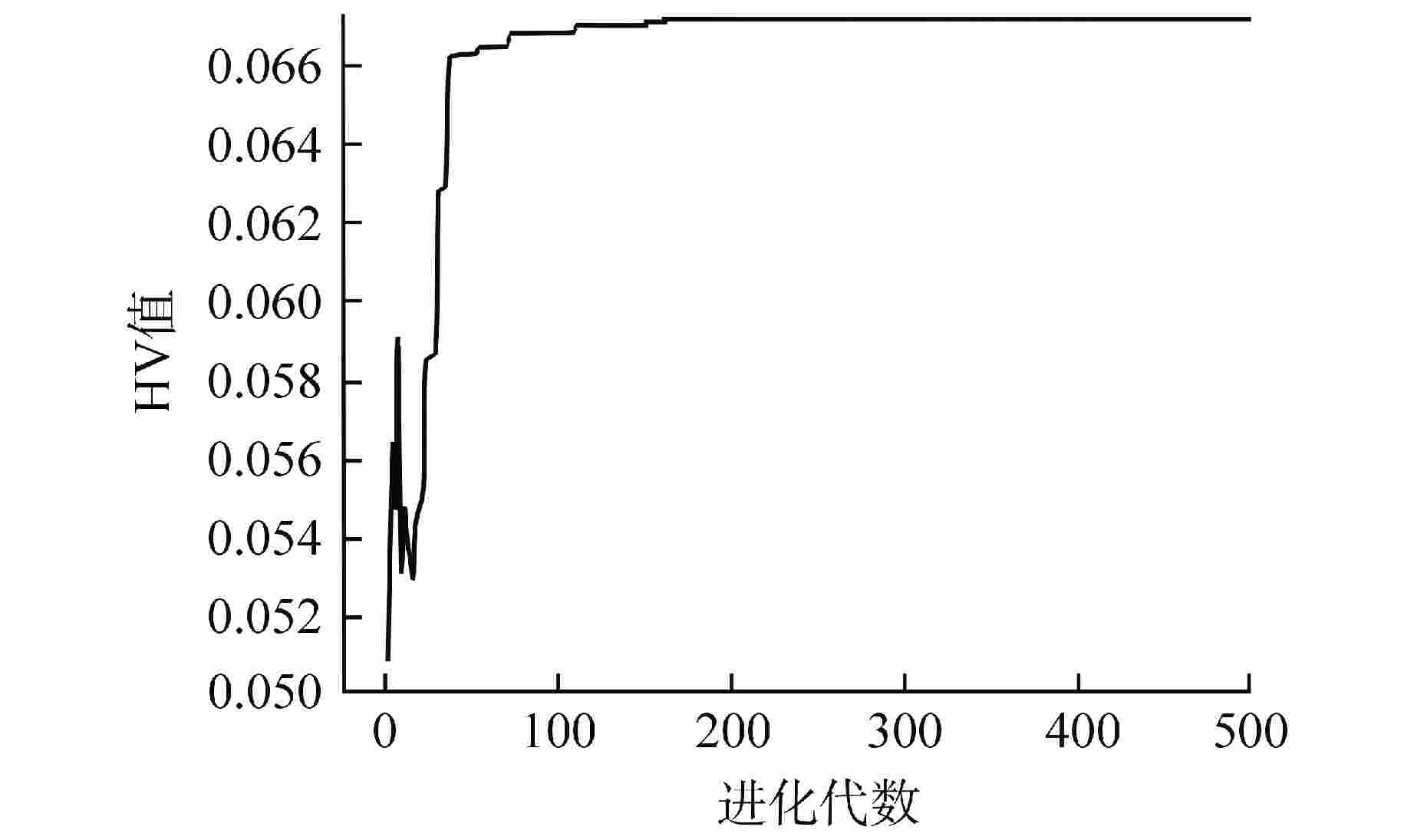
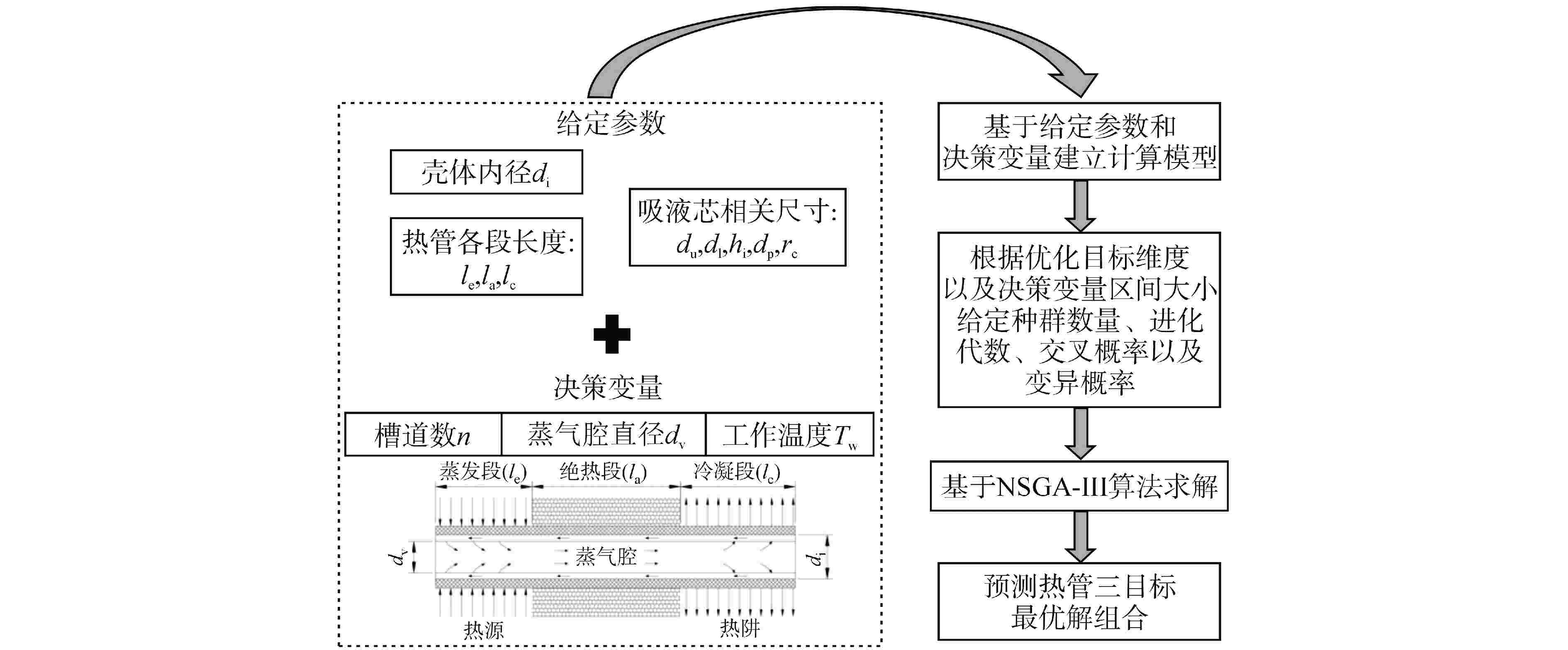
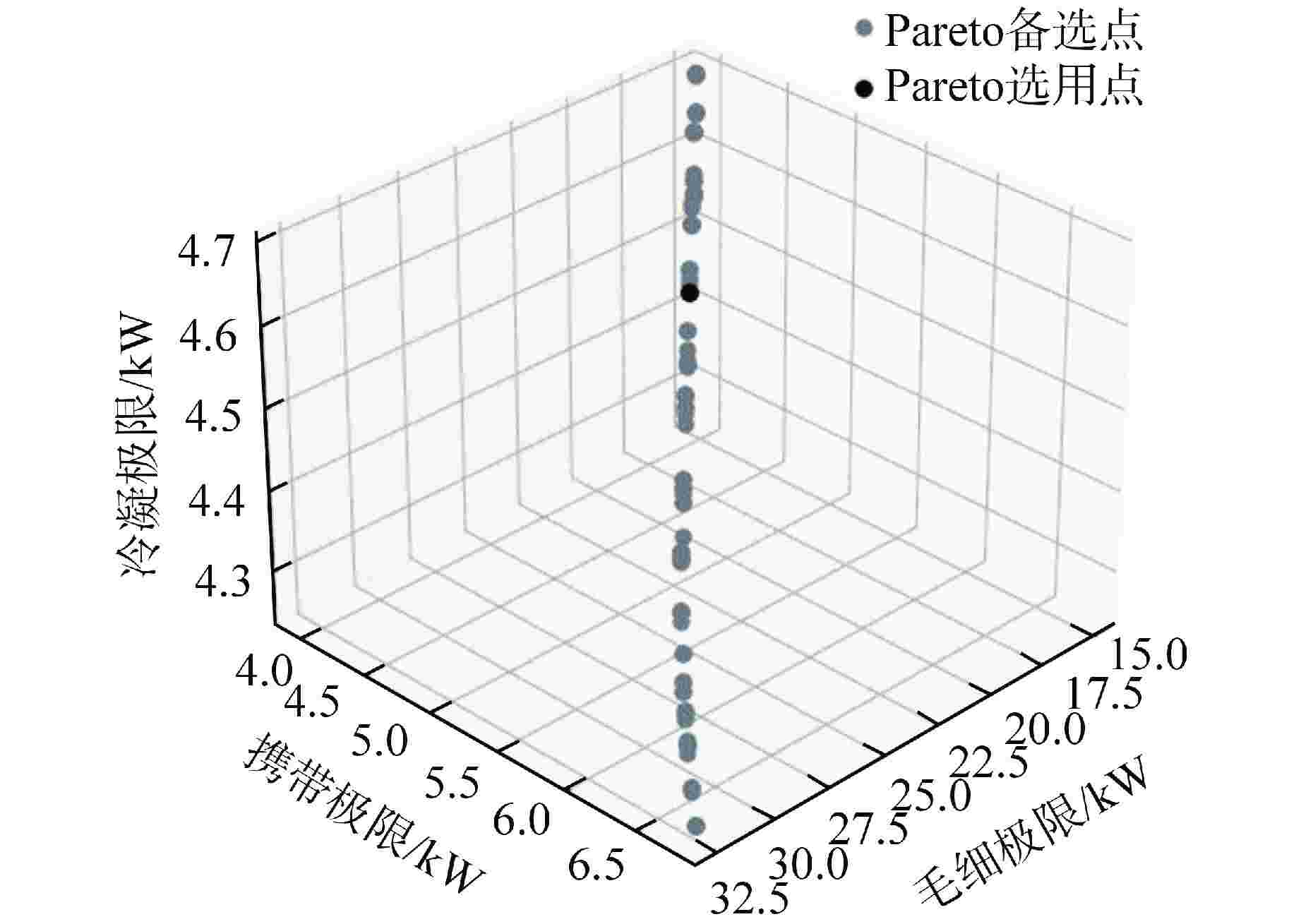
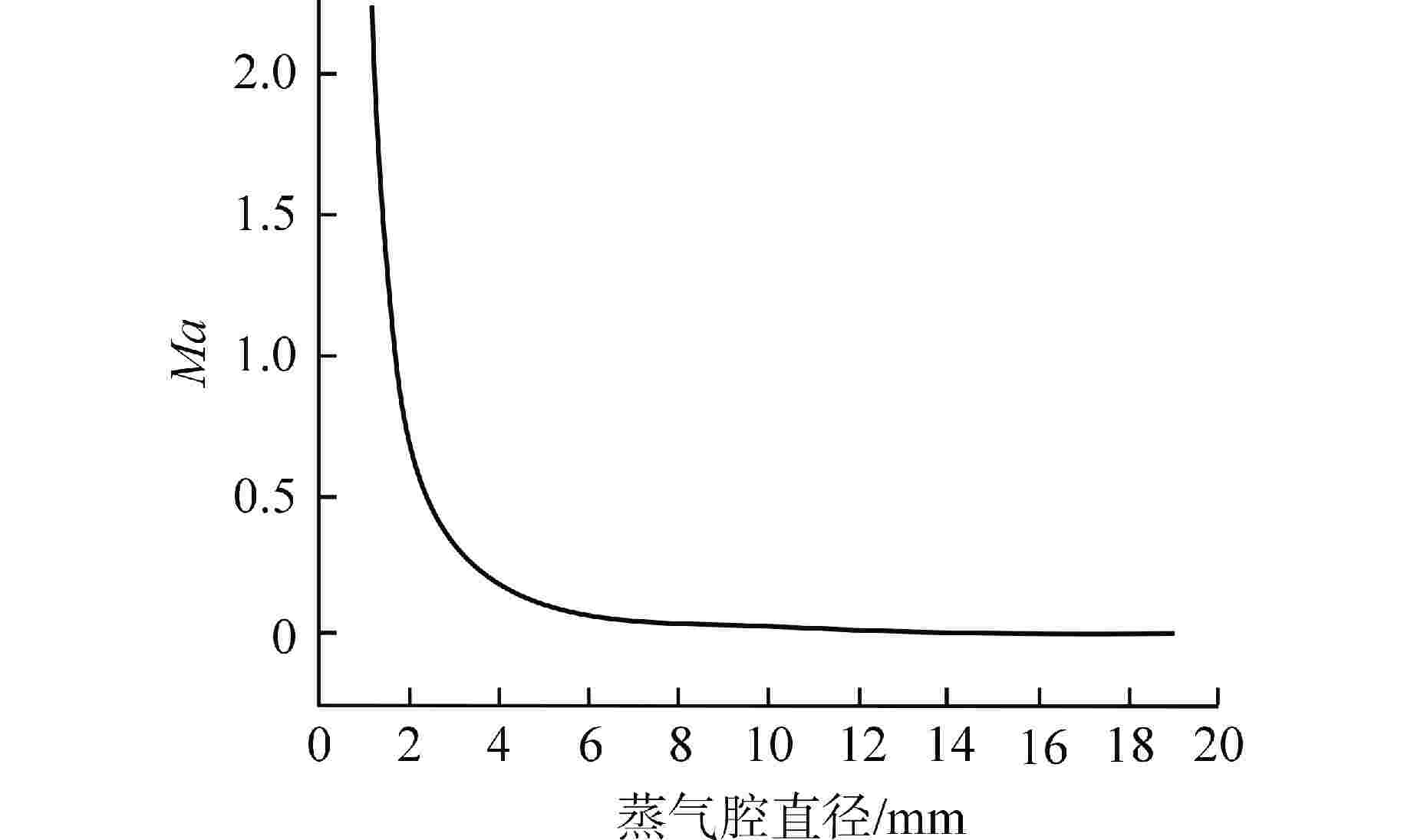
摘要: 碱金属钠热管由于具有工作温度高、传热性能好的特点,因此在高超声速飞行器,微型核反应堆以及太阳能等领域应用前景广阔。本文针对某热管冷却空间核反应堆需要,设计了一种梯形槽道钠热管,并基于NSGA-Ⅲ的遗传学算法,研究了工作温度、蒸气腔直径和槽道数对钠热管传热极限的影响,提出了在热管冷却空间核反应堆服役条件下钠热管传热能力的最优解方案。研究发现,毛细极限随温度升高先升高后降低,在工作温度范围内,携带极限和冷凝极限易成为所设计热管的传热极限,当工作温度为1256 K,蒸气腔直径为12.8 mm,槽道数为20时,所设计热管的传热极限为4.56 kW。设计的梯形槽道钠热管符合马赫数要求和有效毛细半径要求。Abstract: Alkali metal sodium heat pipe has broad application prospects in hypersonic aircraft, micro nuclear reactor and utilization of solar energy because of its high operating temperature and great heat transfer performance. In this paper, according to the requirements of a heat pipe cooling space nuclear reactor project, a trapezoidal grooved sodium heat pipe is designed. Based on the genetic algorithm of NSGA-Ⅲ, the effects of different operating temperature, steam chamber diameter and groove number on the heat transfer limit of sodium heat pipe are studied, and the optimal solution of heat transfer capacity of sodium heat pipe under the service condition of heat pipe cooling space nuclear reactor is proposed. The study found that the capillary limit initially increased with temperature, then decreases. Within the working temperature range, both the entrainment limit and the condensation limit were likely to become the heat transfer limit of the designed heat pipe. At an operating temperature of 1256 K, with a vapor chamber diameter of 12.8 mm and 20 grooves, the heat transfer limit of the designed heat pipe was 4.56 kW.The designed trapezoidal grooved sodium heat pipe meets the requirements of Mach number and effective capillary radius.
-
Key words:
- Sodium heat pipe /
- Heat transfer limit /
- Genetic Algorithm /
- NSGA-Ⅲ
-
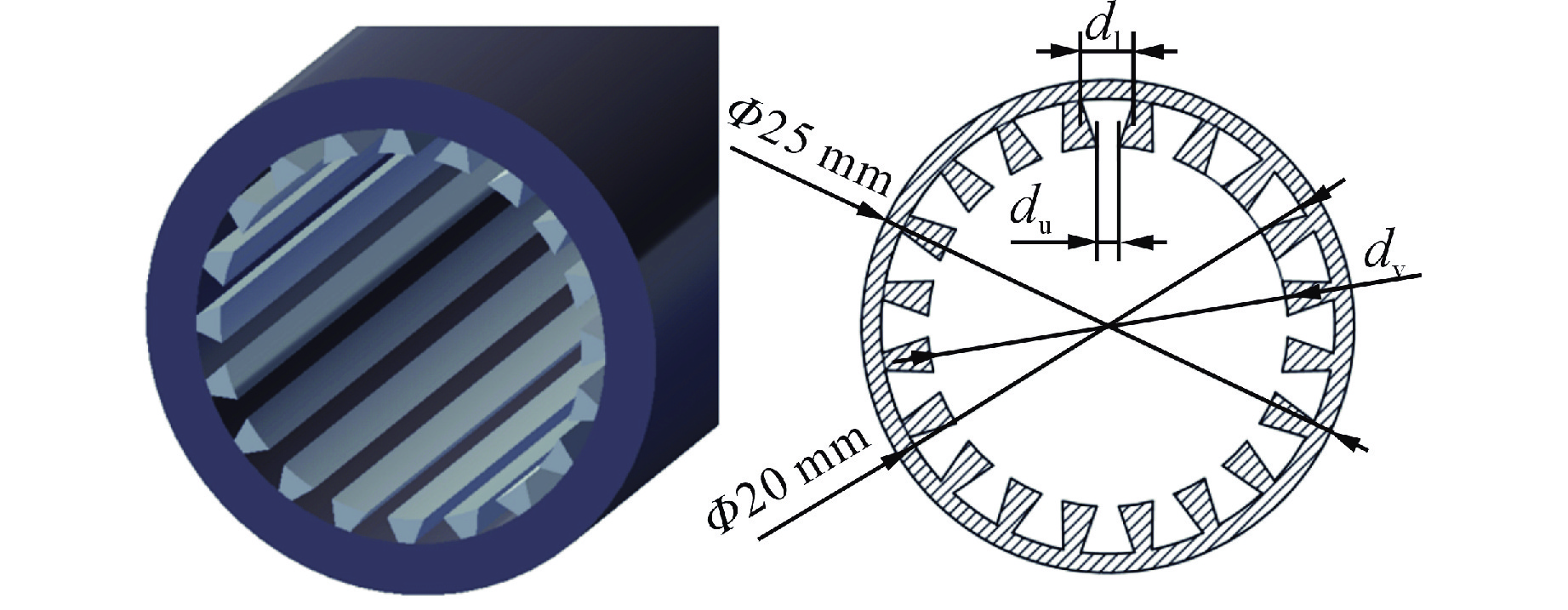
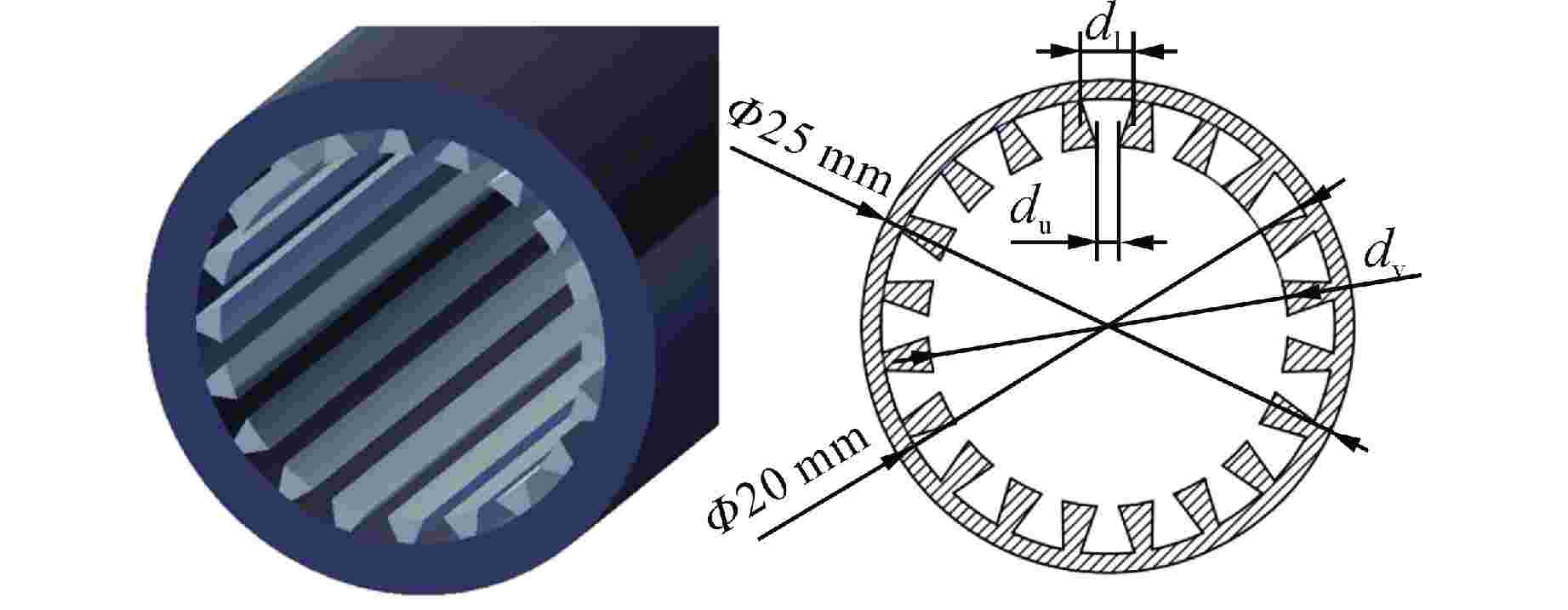
表 1 热管基本参数
Table 1. Basic Parameters of Heat Pipe
壳体材料 壳体外
径$ {d}_{\mathrm{o}} $/mm壳体内
径$ {d}_{\mathrm{i}} $/mm蒸发段
长$ {l}_{\mathrm{e}} $/mm绝热段
长$ {l}_{\mathrm{a}} $/mm冷凝段
长$ {l}_{\mathrm{c}} $/mm沟槽比
$ {d}_{\mathrm{u}} $/$ {d}_{\mathrm{l}} $因科镍-600 25 20 300 300 400 0.4 表 2 钠的物性参数
Table 2. Physical Property Parameters of Sodium
物性参数 描述 气体常数$ R\mathrm{_v} $ $ R_{\mathrm{v}}=361.6355 $ 饱和蒸气压$ p $/Pa $ p=2.09\times10^{11}\times T_{_{\mathrm{w}}}^{-0.5}\times10^{-5576/T_{_{\mathrm{w}}}} $ 液体动力粘度$ \mu_1 $/(Pa·s) $ \mu_1=\mathrm{ }6.083\times10^{-9}\times T_{_{\mathrm{w}}}+1.2606\times10^{-5} $ 液体密度$ \rho_1 $/(kg·m−3) $ \rho_1=950.05-0.2298\times T_{_{\mathrm{w}}} $ 表面张力$ \delta $/(N·m−1) $ \delta=0.232-1.0\times10^{-4}\times T_{_{\mathrm{w}}} $ 汽化潜热$ h $/(J·kg−3) $ h=4.63644\times10^6-180.817\times T_{_{\mathrm{w}}} $ 气体密度$ \rho_{\mathrm{\mathrm{v}}} $/(kg·m−3) $ \rho\mathrm{_v}=(p\times M)/\left(R\mathrm{_u}\times T_{_{\mathrm{w}}}\right) $ 气体动力粘度$ \mu_{\mathrm{v}} $/(Pa·s) $ \mu_{\mathrm{v}}=\mathrm{ }6.083\times10^{-9}\times T_{_{\mathrm{w}}}+1.2606\times10^{-5} $ 工质导热系数$ \lambda\mathrm{_l} $/[W·(m·K)−1] $ \lambda\mathrm{_l}=92.95-0.0581\times T_{_{\mathrm{w}}}+1.17274\times10^{-5}\times T_{_{\mathrm{w}}}^2 $ Tw—热管的工作温度;M—工质摩尔质量;Ru—通用气体常数 表 3 各传热极限值
Table 3. List of Heat Transfer Limits
传热极限名称 数值/kW 毛细极限 19.62 声速极限 107.21 携带极限 4.66 沸腾极限 58.33 粘性极限 12601.76 冷凝极限 4.56 -
[1] SUH J S, PARK Y S. Analysis of thermal performance in a micro flat heat pipe with axially trapezoidal groove[J]. Tamkang Journal of Science and Engineering, 2003, 6(4): 201-206. [2] ANAND A R. Investigations on effect of evaporator length on heat transport of axially grooved ammonia heat pipe[J]. Applied Thermal Engineering, 2019, 150: 1233-1242. doi: 10.1016/j.applthermaleng.2019.01.078 [3] 朱旺法,陈永平,张程宾,等. 燕尾形轴向微槽热管的流动和传热特性[J]. 宇航学报,2009, 30(6): 2380-2386. doi: 10.3873/j.issn.1000-1328.2009.06.053 [4] 颜吟雪,李春林,赵振明,等. 一种微型槽道热管的性能分析与试验研究[J]. 航天返回与遥感,2013, 34(5): 56-62. doi: 10.3969/j.issn.1009-8518.2013.05.008 [5] GOMAA A, RADY W A, YOUSSEF A Z, et al. Thermal performance of heat pipe at different internal groove ratios and working fluids: an experimental investigation[J]. Thermal Science and Engineering Progress, 2023, 41: 101827. doi: 10.1016/j.tsep.2023.101827 [6] 庄骏,张红. 热管技术及其工程应用[M]. 北京: 化学工业出版社,2001: 31-64. [7] 冯踏青. 液态金属高温热管的理论和试验研究[D]. 杭州: 浙江大学,1998. [8] CHI S W. 热管理论与实用[M]. 蒋章焰,译. 北京: 科学出版社,1981: 186-214. [9] LIU Y, YOU K, JIANG Y T, et al. Multi-objective optimal scheduling of automated construction equipment using non-dominated sorting genetic algorithm (NSGA-III)[J]. Automation in Construction, 2022, 143: 104587. doi: 10.1016/j.autcon.2022.104587 [10] ZHOU W, SUN G, MIWA S, et al.An intelligent optimization method for the HCSB blanket based on an improved multi-objective NSGA-III algorithm and an adaptive BP neural network[J].Nuclear Engineering and Technology, 2023, 55(9):3150-3163. [11] 张斌. 参数对简单遗传算法性能的影响[J]. 榆林学院学报,2008, 18(4): 48-49. doi: 10.3969/j.issn.1008-3871.2008.04.017 [12] LI X M, SONG Y M, MAO J, et al. Many-objective rapid optimization of reactor shielding design based on NSGA-III[J]. Annals of Nuclear Energy, 2022, 177: 109322. doi: 10.1016/j.anucene.2022.109322 [13] 胡崇举,余大利,何梅生,等. 超高温锂热管设计与热输运性能分析[J]. 核动力工程,2022, 43(3): 21-27. -





 下载:
下载: