基于多次碰撞源的离散纵标射线效应减弱方法研究

郑征; 李翔; 梅其良; 黎辉; 王梦琪

doi:10.13832/j.jnpe.2025.01.0036

基于多次碰撞源的离散纵标射线效应减弱方法研究

doi: 10.13832/j.jnpe.2025.01.0036

上海核工程研究设计院股份有限公司，上海，200233

基金项目: 国家重点研发计划项目（2022YFB1902800）

详细信息

作者简介:
郑　征（1985—），男，博士，现主要从事核电厂辐射屏蔽设计工作，E-mail: zhengzheng@snerdi.com.cn

中图分类号: TL328
计量
- 文章访问数: 12
- HTML全文浏览量: 3
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-09
- 修回日期: 2024-05-09
- 刊出日期: 2025-02-15

Study on the Attenuation Method of Discrete Ordinate Ray Effect Based on Multiple Collision Source

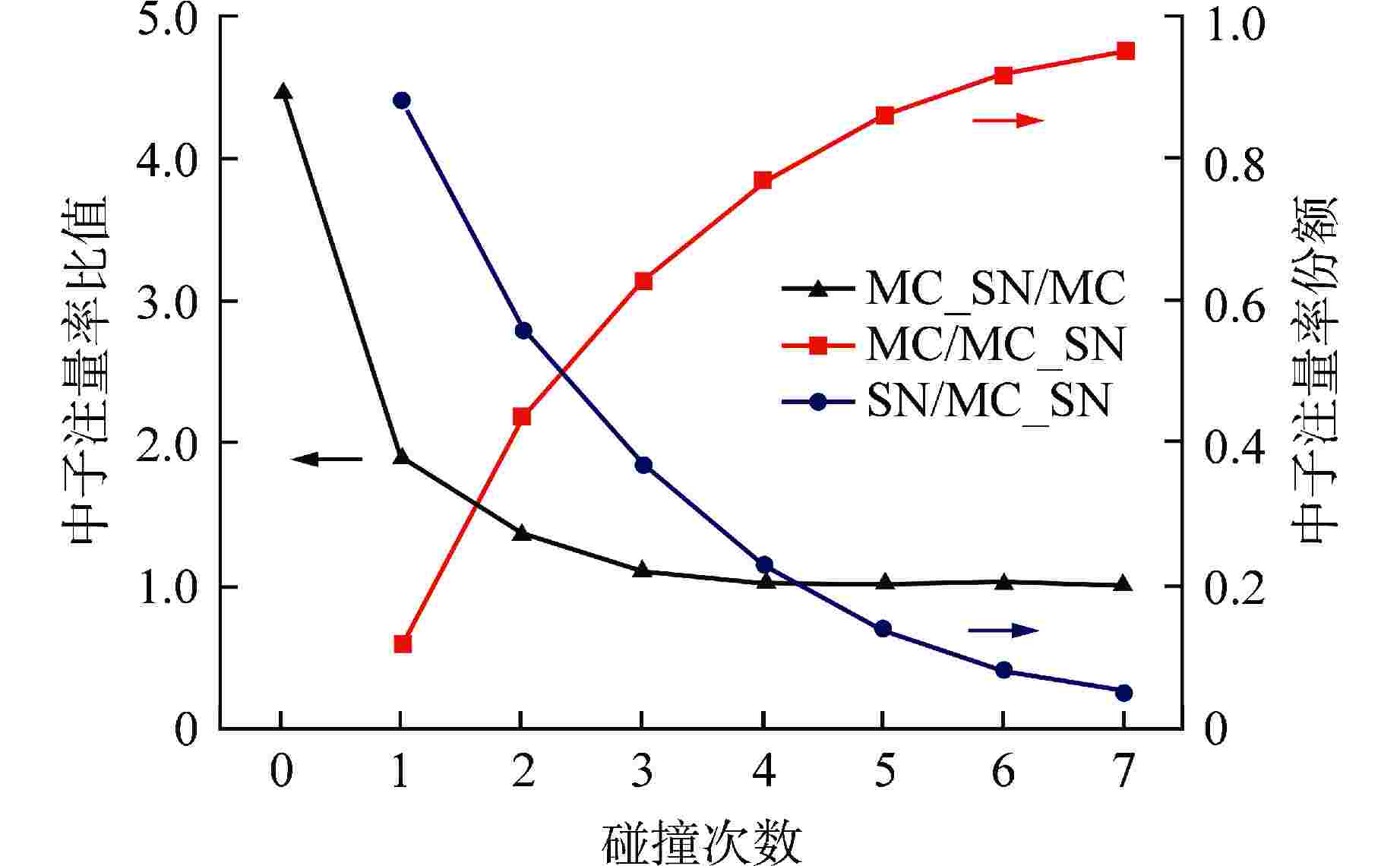
Shanghai Nuclear Engineering Research and Design Institute Co., Ltd., Shanghai, 200233, China

摘要

摘要: 本研究旨在探讨通过蒙特卡罗（MC）方法计算多次碰撞源分布，以减轻离散纵标（SN）方法中的射线效应，尤其是在处理包含局部源、低密度或真空区域的模型时。采用MC方法计算多次碰撞源分布，并利用Kobayashi基准题对多次碰撞源和首次碰撞源的射线效应减弱方法进行了初步验证和分析。通过混合并行技术（消息传递接口MPI+开放式多处理器OpenMP）提高计算效率，减少负载不平衡问题。研究表明，MC多次碰撞源方法在抑制SN方法中局部源问题的射线效应方面表现优异，能够显著减少计算中的非物理震荡，提高计算精度。当碰撞次数达到3次以上时，计算偏差降低至10%以下。此外，采用混合并行技术后，120个线程的并行计算效率达到80%以上。尽管在计算时间上略有不足，该方法在处理复杂几何和物理条件下展现了较大的潜力，是一种有前景的射线效应减弱方法。
- 蒙特卡罗 /
- 离散纵标 /
- 多次碰撞源 /
- 首次碰撞源 /
- 射线效应 /
- 混合并行
Abstract: This study aims to explore the use of the Monte Carlo (MC) method to calculate multi-collision source distributions, so as to mitigate the ray effect in the discrete ordinates (SN) method, particularly in models with localized sources, low-density regions, or vacuum areas. The distribution of multiple collision sources is calculated by MC method, and the method of reducing the ray effect of multiple collision sources and first collision sources is preliminarily verified and analyzed by Kobayashi benchmark problem. Through hybrid parallel technique (message passing interface MPI + open multiprocessor OpenMP), the computational efficiency is improved and the load imbalance problem is reduced. The study shows that the MC multi-collision source method effectively suppresses the ray effect in localized source problems within the SN method, significantly reducing non-physical oscillations and improving computational accuracy. When the number of collisions exceeds three, the computational deviation is reduced to below 10%. Furthermore, the use of hybrid parallel computing resulted in a parallel efficiency exceeding 80% with 120 threads. Although this method has a slight drawback in terms of computational time, it shows great potential for addressing complex geometries and physical conditions, making it a promising approach for reducing the ray effect.
- Monte Carlo /
- Discrete ordinate /
- Multiple collision source /
- First collision source /
- Ray effect /
- Hybrid parallel

HTML全文

图 1 Kobayashi基准题几何描述

Figure 1. Geometry Description of Kobayashi Benchmark Problems

下载: 全尺寸图片幻灯片

图 2 立方体空腔屏蔽问题的中子注量率比值和份额随碰撞次数变化

Figure 2. Cubic Inner-void Shielding Problem: Variation of Neutron Fluence Rate Ratio and Fraction with Collision Times

下载: 全尺寸图片幻灯片

图 3 中子注量率分布

黑色实线—MC_SN；红色虚线—MC；蓝色实线—SN；背景—SN

Figure 3. Distribution of Neutron Fluence Rate

下载: 全尺寸图片幻灯片

图 4 中子注量率比值分布

Figure 4. Distribution of Neutron Fluence Rate Ratio

下载: 全尺寸图片幻灯片

表 1 Kobayashi基准题源强和单群截面

Table 1. Kobayashi Benchmark Source and One-group Cross Section

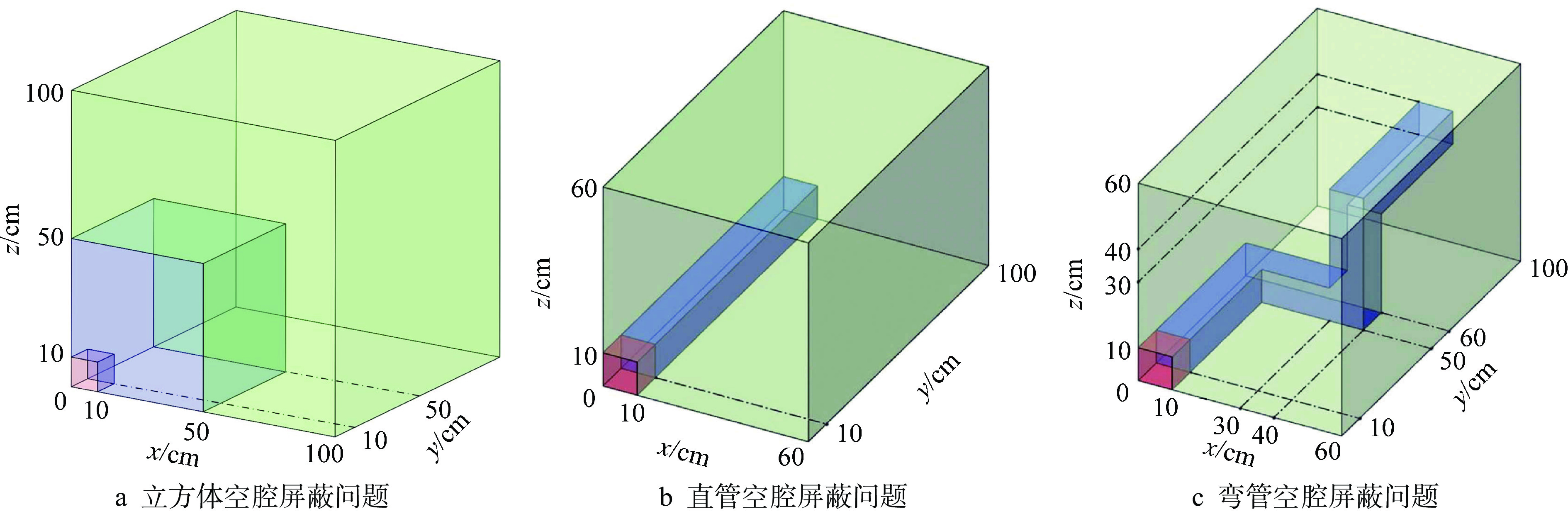
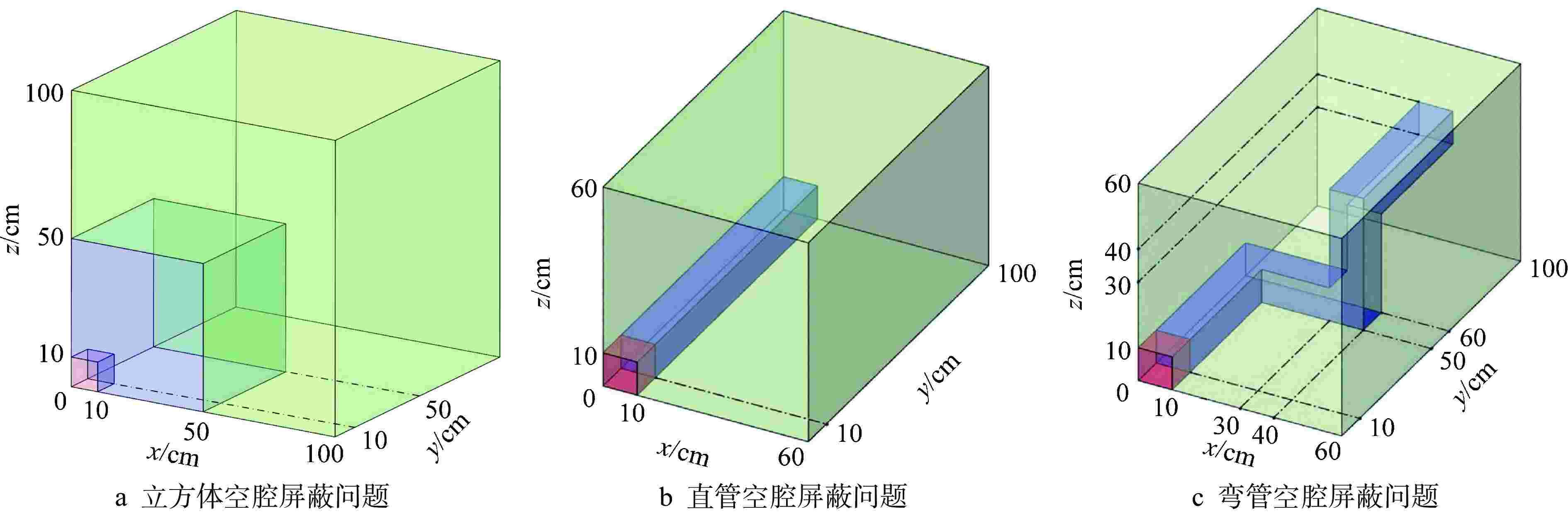
区域	Q/(cm⁻³·s⁻¹)	Σ_t/cm⁻¹	Σ_s（情况1）/cm⁻¹	Σ_s（情况2）/cm⁻¹
源区	1	0.1	0	0.05
真空区	0	10⁻⁴	0	0.5×10⁻⁴
屏蔽区	0	0.1	0	0.05

下载: 导出CSV

表 2 立方体空腔屏蔽问题计算时间

Table 2. Cubic Inner-void Shielding Problem Calculation Time

碰撞次数	MC计算时间/s	SN计算时间/s
0	147	9.15
1	166	8.02
2	199	7.48
3	207	7.52
4	203	7.52
5	209	6.98
6	234	7.04
7	238	7.04

下载: 导出CSV

表 3 首次碰撞源方法计算效率

Table 3. Efficiency of First Collision Source Method

进程数目	线程数目/ 每个进程	总线程数目	计算时间/s	加速比	并行效率/%
1	1	1	1372.4	1.0	−
2	10	20	71.0	19.3	97
4	10	40	36.6	37.5	94
8	10	80	19.2	71.5	89
12	10	120	13.9	98.5	82

下载: 导出CSV

参考文献(13)

[1]	CARLSON B G. Solution of the transport equation by sn approximations, LA-1891[R]. Los Alamos: Los Alamos National Lab. , 1955.
[2]	LATHROP K D. Ray effects in discrete ordinates equations[J]. Nuclear Science and Engineering, 1968, 32(3): 357-369. doi: 10.13182/NSE68-4
[3]	ALCOUFFE R E. A first collision source method for coupling Monte Carlo and discrete ordinates for localized source problems[M]//ALCOUFFE R, DAUTRAY R, FORSTER A, et al. Monte-Carlo Methods and Applications in Neutronics, Photonics and Statistical Physics. Berlin: Springer, 1985: 352-366.
[4]	胡也,陈义学,张斌,等. 基于首次碰撞源方法的多维SN射线效应研究[J]. 原子能科学技术,2013, 47(S1): 9-14.
[5]	杨超,李志鹏,于涛,等. 基于全局因子修正首次碰撞源的射线效应方法研究[J]. 核动力工程,2023, 44(3): 54-58.
[6]	张斌. 基于目标导向的角度自适应射线效应消除方法研究[D]. 北京: 华北电力大学,2018.
[7]	王新宇,张斌,陈义学. 基于多次碰撞源的屏蔽计算方法研究[J]. 原子能科学技术,2020, 54(5): 811-819. doi: 10.7538/yzk.2019.youxian.0557
[8]	HERRING N F, YESSAYAN R A, BEYER K A, et al. Ray effects mitigation through monte carlo coupling for detector problems[C]//International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering, M and C. Portland: American Nuclear Society, 2019: 2228-2237.
[9]	ZHANG G C, HAO C Y, LIU K, et al. Ray effects mitigation using the Monte Carlo first collision source method and application to the Kobayashi benchmark problems[J]. Annals of Nuclear Energy, 2022, 169: 108902. doi: 10.1016/j.anucene.2021.108902
[10]	KOBAYASHI K, SUGIMURA N, NAGAYA Y. 3D radiation transport benchmark problems and results for simple geometries with void region[J]. Progress in Nuclear Energy, 2001, 39(2): 119-144. doi: 10.1016/S0149-1970(01)00007-5
[11]	DENG L, LI G, ZHANG B Y, et al. A high fidelity general purpose 3-D Monte Carlo particle transport program JMCT3.0[J]. Nuclear Science and Techniques, 2022, 33(8): 108. doi: 10.1007/s41365-022-01092-0
[12]	CHENG T P, MO Z Y, YANG C, et al. JSNT-S: a parallel 3D discrete ordinates radiation transport code on structured mesh[C]//2018 26th International Conference on Nuclear Engineering. London: ASME, 2018.
[13]	KONNO C. TORT solutions with FNSUNCL3 for Kobayashi's 3D benchmarks[J]. Progress in Nuclear Energy, 2001, 39(2): 167-179. doi: 10.1016/S0149-1970(01)00010-5