冲击载荷作用下高能管道塑性大变形的最大挠度预测方法

顾睿杰; 董成武; 何建; 孙晓丹; 姚迪

doi:10.13832/j.jnpe.2025.01.0216

冲击载荷作用下高能管道塑性大变形的最大挠度预测方法

doi: 10.13832/j.jnpe.2025.01.0216

顾睿杰^1,,
董成武¹,
何建^1, ,,
孙晓丹¹,
姚迪²

1.
哈尔滨工程大学航天与建筑工程学院，哈尔滨，150001
2.
中国核动力研究设计院，成都， 610213

基金项目: 国家自然科学基金项目（52278297）

详细信息

作者简介:
顾睿杰（1999—），男，硕士研究生，现主要从事高能管道甩击方面的研究，E-mail: 1834745617@qq.com

通讯作者:
何　建，E-mail: hejian@hrbeu.edu.cn

中图分类号: TL353.13；O347.3
计量
- 文章访问数: 11
- HTML全文浏览量: 9
- PDF下载量: 2
- 被引次数: 0
出版历程
- 收稿日期: 2024-04-21
- 修回日期: 2024-10-10
- 刊出日期: 2025-02-15

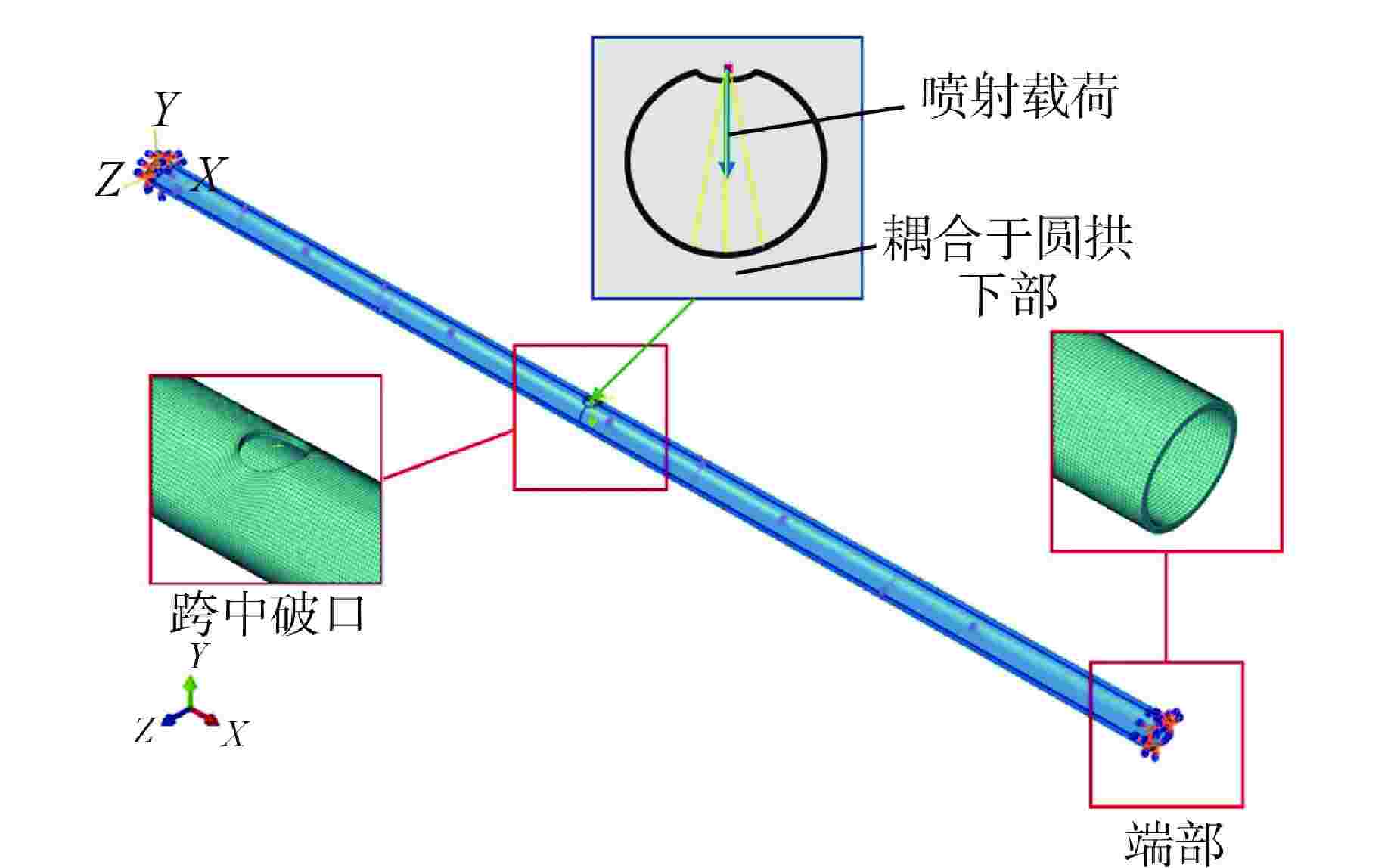
Maximum Deflection Prediction Method for Plastic Large Deformation of High-energy Pipelines under Impact Load

Gu Ruijie^1
,,
Dong Chengwu¹,
He Jian^{1
, ,},
Sun Xiaodan¹,
Yao Di²

1.
College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin, 150006, China
2.
Nuclear Power Institute of China, Chengdu, 610213, China

摘要

摘要: 高能管道在冲击载荷的作用下，结构会发生大挠度变形。为了预测高能管道的最大变形挠度，本文基于膜力因子法（MFM）推导了适用于该结构的膜力因子，建立了相较于传统方法更便捷的跨中挠度计算方法，并与数值模拟结果和试验结果进行了对比，验证了其准确性。研究结果表明：MFM对管道结构挠度预测有较高的准确度；跨中挠度的大小由变量因子控制，跨中挠度随着冲击荷载与管道长度的增加而增加，随着塑性极限弯矩的增加而减小。由于MFM未考虑截面塌陷所耗散的能量，所以对于椭圆化程度较高的管道，挠度预测结果与实际情况相比偏大，但是由于管道内部高能流体的支承，管道的塌陷效应不明显，因此该方法可用于对高能管道大挠度变形进行预测。针对塌陷程度较高的管道，结合塌陷模型对MFM预测结果进行了修正，大大提高了预测方法的准确性。
- 膜力因子法（MFM） /
- 跨中挠度 /
- 塌陷模型 /
- 高能管道；塑性大变形
Abstract: When high-energy pipelines under the action of impact loads, the structure will subject to large deflection deformation. In order to predict the maximum deformation deflection of high-energy pipelines, a membrane force factor applicable to the structure was derived based on the membrane force factor method (MFM). A more convenient calculation method than traditional methods for mid-span deflection was established, and its accuracy was verified by comparing it with numerical simulation results and experiment results. The research results indicate that MFM has a high accuracy in predicting the deflection of pipeline structures; The magnitude of mid-span deflection is controlled by variable factors. The mid-span deflection increases with the increase of impact load and pipeline length, and decreases with the increase of plastic ultimate bending moment. The predicted deflection of pipelines with high degree of ellipticity is larger than the actual situation beacuse of MFM not taking into account the energy dissipated by section collapse. However, due to the support of high-energy fluid inside the pipeline, the collapse effect of the high-energy pipeline is not obvious. Therefore, this method can be used to predict the large deflection deformation of high-energy pipelines. For pipelines with high degree of collapse, the MFM prediction results are modified by combining the collapse model, which greatly improves the accuracy of the prediction method.
- Membrane force factor method (MFM) /
- Mid-span deflection /
- Collapse model /
- High-energy pipeline, Large plastic deformation

HTML全文

图 1 冲击载荷作用下管道的力学模型

P—冲击载荷

Figure 1. Mechanical Model of Pipelines under Impact Load

下载: 全尺寸图片幻灯片

图 2 圆管结构有限元模型

Figure 2. Finite Element Model of Circular Pipe Structure

下载: 全尺寸图片幻灯片

图 3 伪应变能与总应变能比值时程曲线

Figure 3. Time-history Curve of Ratio of Pseudo-strain Energy to Total Strain Energy

下载: 全尺寸图片幻灯片

图 4 数值模拟应力云图及挠度曲线

Figure 4. Stress Contour and Deflection Curve of Numerical Simulation

下载: 全尺寸图片幻灯片

图 5 不同冲击载荷工况下结构动能时程曲线

Figure 5. Time-history Curves of of Structural Kinetic Energy under Different Impact Loads

下载: 全尺寸图片幻灯片

图 6 不同冲击载荷工况下Abaqus模拟挠度曲线

Figure 6. Abaqus Simulation Deflection Curves under Different Impact Load Conditions

下载: 全尺寸图片幻灯片

图 7 MFM与试验结果对比

Figure 7. Comparison between MFM and Experimental Results　　　　　

下载: 全尺寸图片幻灯片

图 8 高能流体冲击和锥头冲击示意图

Figure 8. Schematic Diagram of High Energy Fluid Impact and Cone Head Impact

下载: 全尺寸图片幻灯片

图 9 理想塌陷模型

Figure 9. Ideal Collapse Model

下载: 全尺寸图片幻灯片

图 10 FEA与MFM预测值及修正值对比

Figure 10. Comparison of Predicted and Corrected Values between FEA and MFM

下载: 全尺寸图片幻灯片

图 11 变量因子-无量纲位移曲线

Figure 11. Variable Factor-Dimensionless Displacement Curve

下载: 全尺寸图片幻灯片

图 12 不同参数下的跨中挠度曲线

Figure 12. Mid-span Deflection Curve with Different Parameters　　　　

下载: 全尺寸图片幻灯片

表 1 管道甩击试验工况参数

Table 1. Conditions of Pipe Whip Test

管道长度/mm	管道半径/mm	管道厚度/mm	压力/ MPa	等效冲击荷载/ kN	温度/K	屈服应力/MPa
3000	25.4	2.6	5	11	553.1	295

下载: 导出CSV

表 2 不同冲击载荷工况下的结果

Table 2. Results under Different Impact Load Conditions

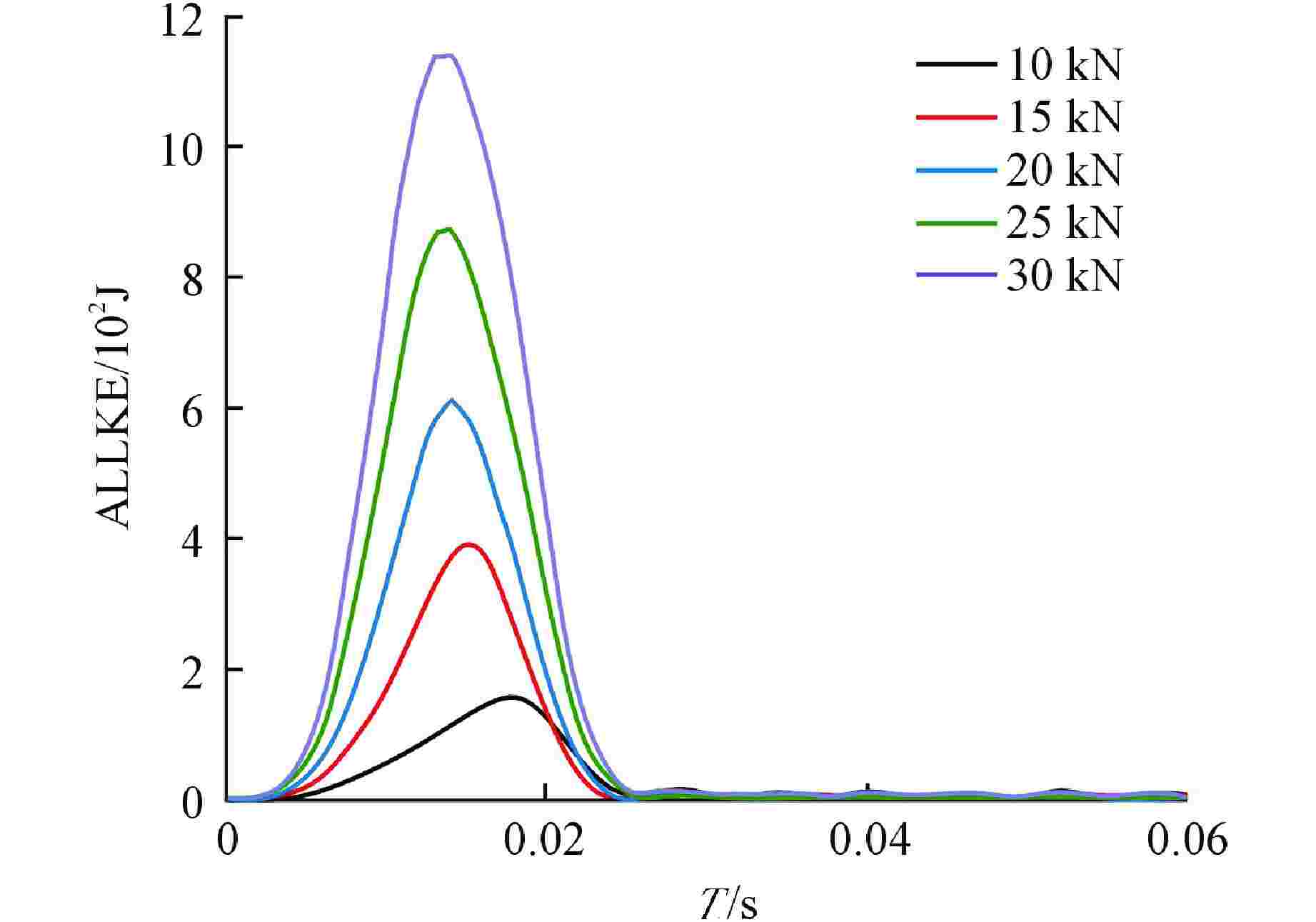
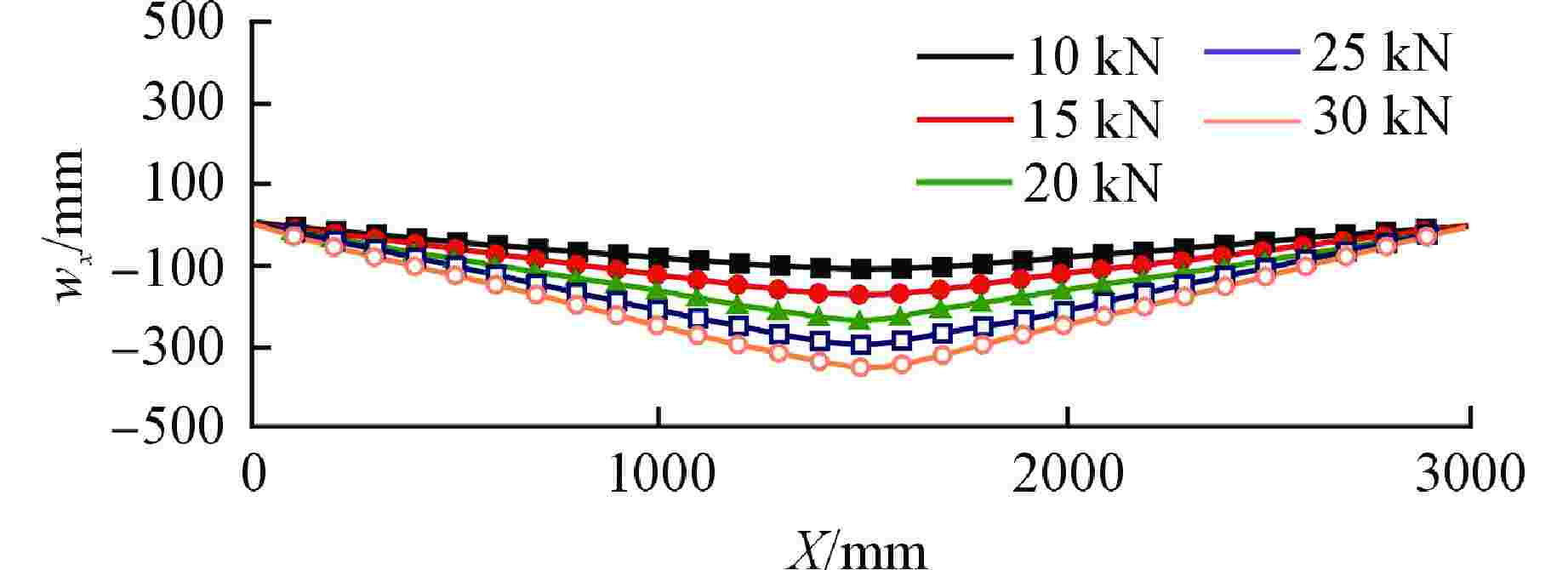
冲击载荷/kN	MFM预测跨中挠度/mm	数值模拟跨中挠度/mm	误差/%
10	−109.850	−107.823	1.845
15	−175.879	−171.221	2.648
20	−239.253	−229.872	3.921
25	−301.731	−296.891	1.604
30	−363.792	−351.575	3.358

下载: 导出CSV

表 3 落锤冲击试验的工况参数

Table 3. Condition Parameters of Drop Hammer Impact Test

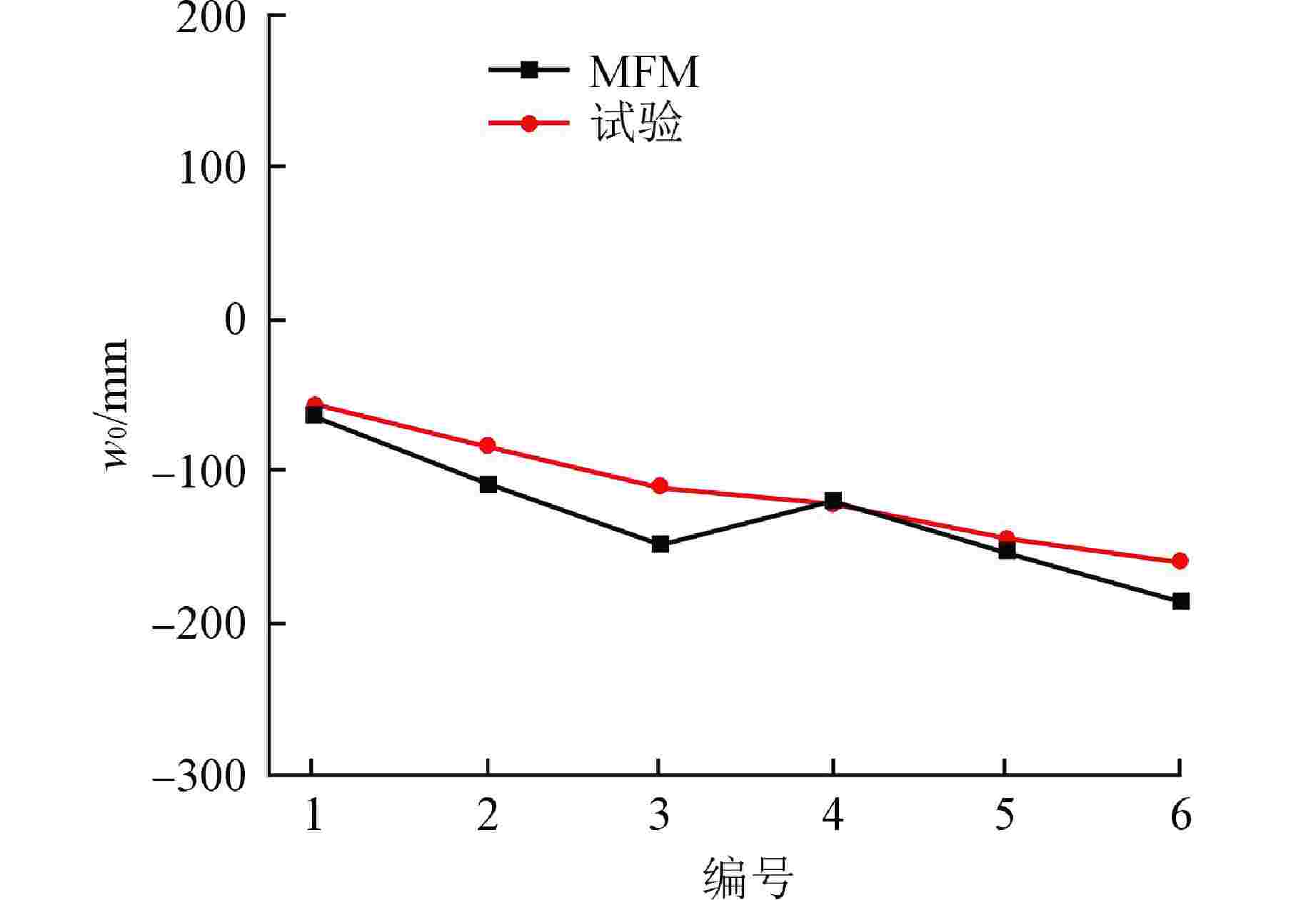
编号	试件代号	质量/kg	高度/mm	直径/mm	壁厚/mm	长度/mm	屈服应力/MPa	挠度/mm
1	B1-WM-1	427	509.8	60	3.5	900	250	−56.42
2	B1-WM-2	427	1012.5	60	3.5	900	250	−83. 11
3	B1-WM-3	427	1703.7	60	3.5	900	250	−110.00
4	D2-WM-1	427	3011.8	114	4.0	1200	275	−120.90
5	D2-WM-2	427	4001.5	114	4.0	1200	275	−144.00
6	D2-WM-3	427	5006.7	114	4.0	1200	275	−159.90

下载: 导出CSV

表 4 FEA工况参数及结果

Table 4. Condition Parameters and Results by FEA

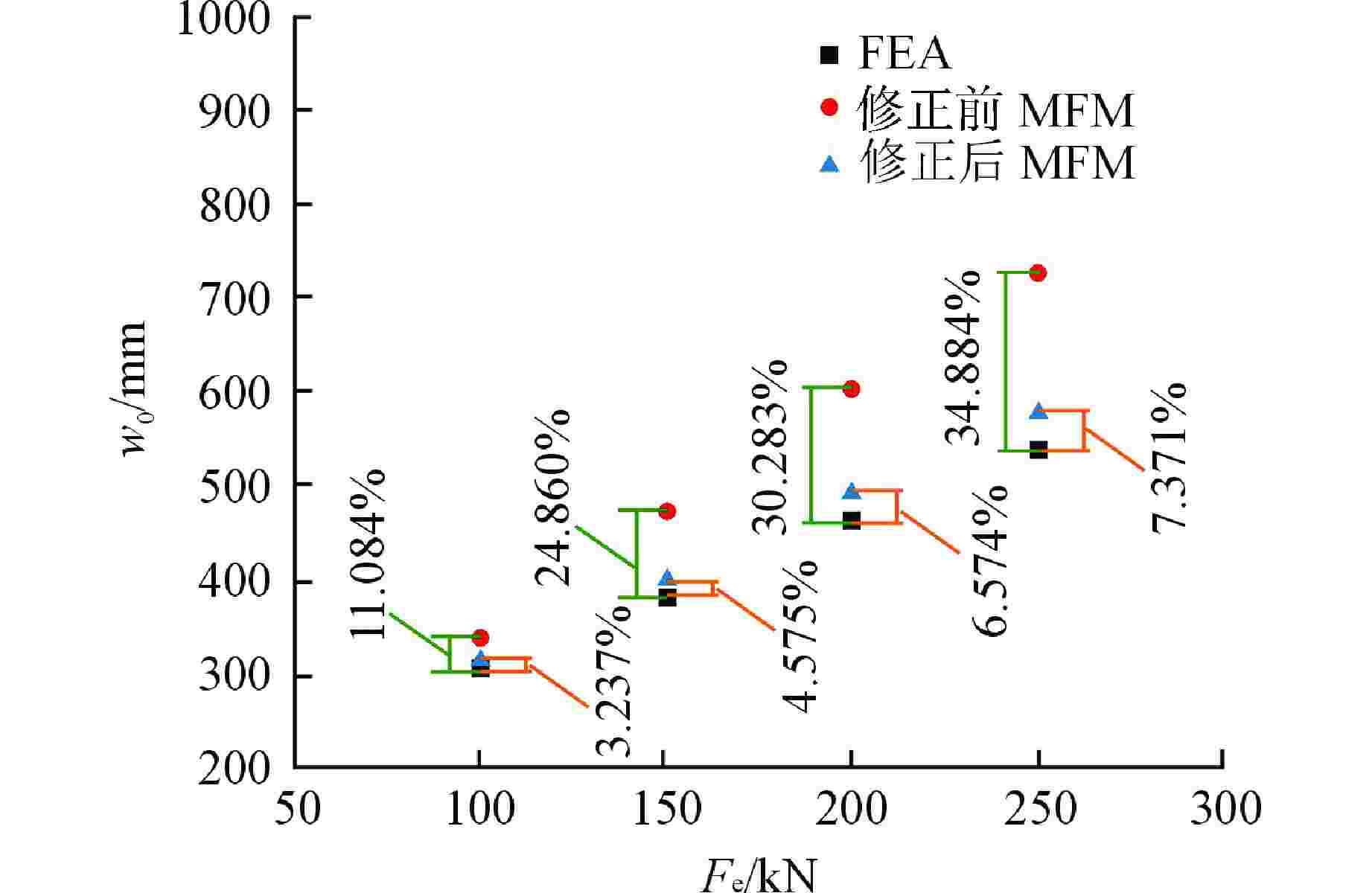
等效喷射载荷/kN	直径/mm	壁厚/mm	长度/mm	温度/K	压强/MPa	FEA结果/mm	MFM结果/mm	误差/%
100	168.3	9.9	6626	613	10	305.472	339.330	11.084
150	168.3	9.9	6626	613	10	381.980	476.940	24. 860
200	168.3	9.9	6626	613	10	463.662	604.073	30.283
250	168.3	9.9	6626	613	10	540.138	728.558	34.884

下载: 导出CSV

表 5 软件计算结果

Table 5. Calculation Results by Software

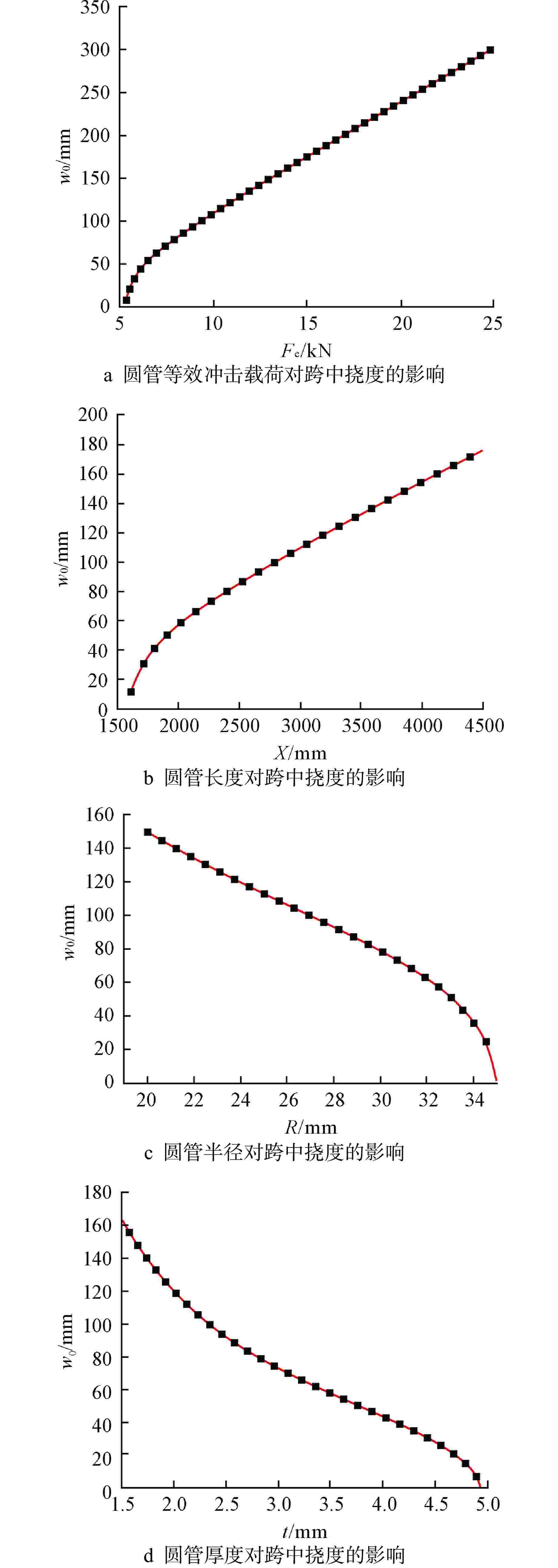
编号	F_e/ kN	管道长度/mm	管道半径/mm	管道厚度/mm	跨中挠度/mm
1	10	3000	25.4	2.6	−109.850
2	20	3000	25.4	2.6	−239.253
3	30	3000	25.4	2.6	−363.792
4	10	2000	25.4	2.6	−57.459
5	10	2500	25.4	2.6	−85.880
6	10	4000	12.7	2.6	−154.353
7	10	3000	38.1	2.6	−243.651
8	10	3000	50.8	2.6	0
9	10	3000	25.4	2.6	0
10	10	3000	25.4	1.0	−314.168
11	10	3000	25.4	2.0	−150.007
12	10	3000	25.4	3.5	−71.537

下载: 导出CSV

参考文献(16)

[1]	CHEN K S, SHEN W Q. Further experimental study on the failure of fully clamped steel pipes[J]. International Journal of Impact Engineering, 1998, 21(3): 177-202 . doi: 10.1016/S0734-743X(97)00083-3
[2]	BROOKER D C. Denting of pressurised pipelines under localised radial loading[J]. International Journal of Mechanical Sciences, 2004, 46(12): 1783-1805. doi: 10.1016/j.ijmecsci.2004.11.004
[3]	KARAMANOS S A, ANDREADAKIS K P. Denting of internally pressurized tubes under lateral loads[J]. International Journal of Mechanical Sciences, 2006, 48(10): 1080-1094.
[4]	李晨,闫秋实,李亮,等. 侧向冲击荷载作用下不锈钢管混凝土柱的力学性能研究[J]. 防护工程,2019, 41(6): 7-14.
[5]	姜珊,路国运,杨会伟. 侧向冲击载荷下钢管混凝土结构的动力响应及参数分析[J]. 爆炸与冲击,2023, 43(11): 112203. doi: 10.11883/bzycj-2023-0039
[6]	余同希,田岚仁,朱凌. 强脉冲载荷作用下结构塑性大变形的最大挠度直接预测[J]. 力学学报,2023, 55(5): 1113-1123. doi: 10.6052/0459-1879-22-607
[7]	郭君,张文启,郭建军,等. 水下爆炸冲击波作用下单向加筋板的大挠度塑性变形[J]. 兵工学报,2015, 36(S1): 163-168.
[8]	张新春,王俊瑜,汪玉林,等. 基于膜力因子法的方形锂离子电池冲击动力响应研究[J]. 应用数学和力学,2022, 43(11): 1203-1213.
[9]	YU T X, STRONGE W J. Large deflections of a rigid-plastic beam-on-foundation from impact[J]. International Journal of Impact Engineering, 1990, 9(1): 115-126. doi: 10.1016/0734-743X(90)90025-Q
[10]	杨桂通. 弹塑性力学引论[M]. 北京: 清华大学出版社,2004: 55-58.
[11]	YOUNGDAHL C K. Correlation parameters for eliminating the effect of pulse shape on dynamic plastic deformation[J]. Journal of Applied Mechanics, 1970, 37(3): 744-752.
[12]	ZHU L, TIAN L R, CHEN F L, et al. A new equivalent method for complex-shaped pulse loading based on saturation analysis and membrane factor method[J]. International Journal of Impact Engineering, 2021, 158: 104018. doi: 10.1016/j.ijimpeng.2021.104018
[13]	REID S R, YU T X, YANG J L, et al. Dynamic elastic-plastic behaviour of whipping pipes: experiments and theoretical model[J]. International Journal of Impact Engineering, 1996, 18(7-8): 703-733. doi: 10.1016/S0734-743X(96)00034-6
[14]	张荣. 建筑用圆钢管构件侧向冲击响应及失效机理[D]. 哈尔滨: 哈尔滨工业大学,2018.
[15]	FURNES O, AMDAHL J. Ship collisions with offshore platforms[C]. In: Proceedings of Intermaritec, Hamburg, Germany; 1980; 310–318.
[16]	余同希,邱信明. 冲击动力学[M]. 北京: 清华大学出版社,2011: 199.