Experimental Study on the Strength Probability Distribution of a Domestic Fine-Grained Nuclear Graphite
-
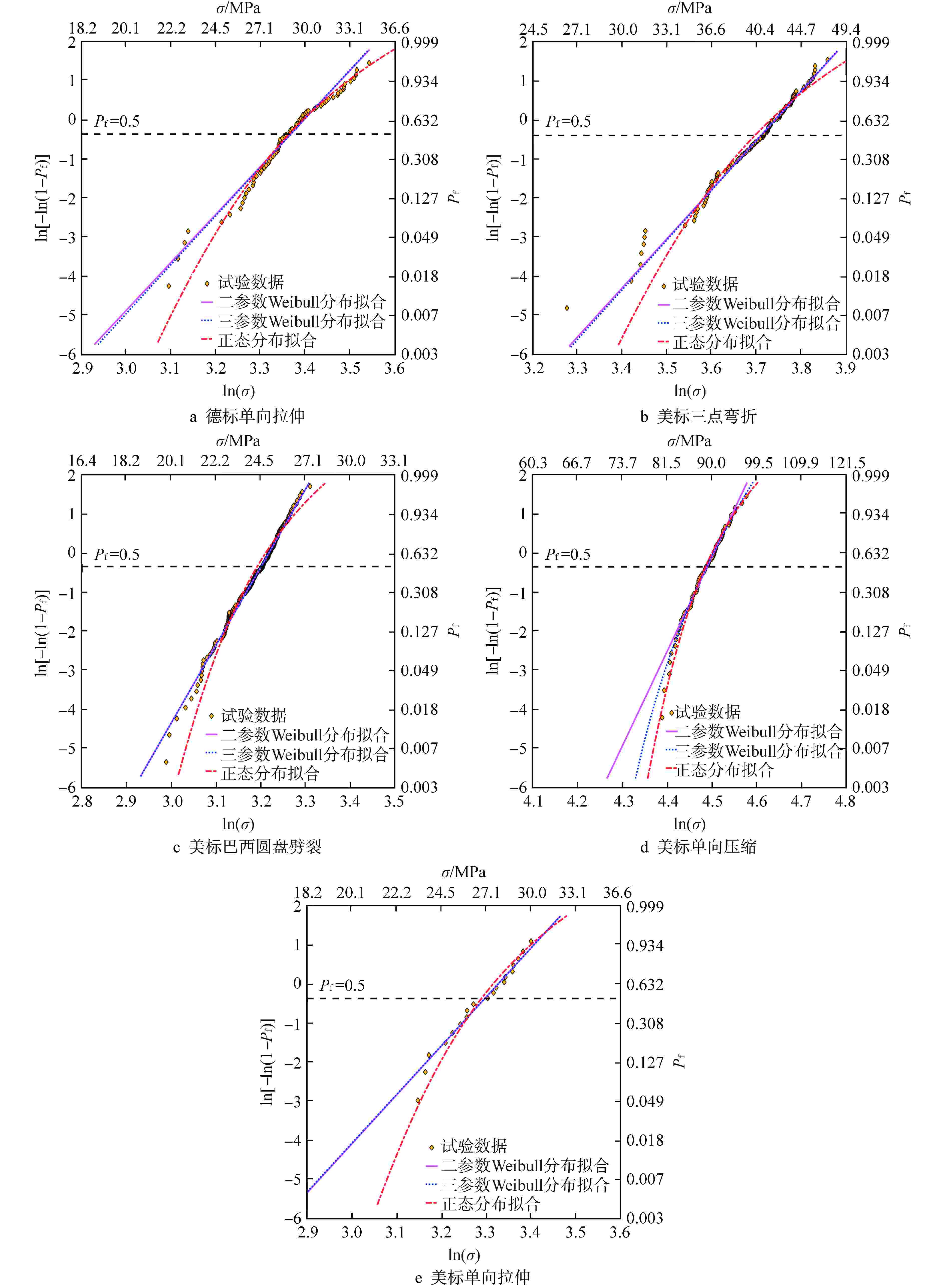
摘要: 针对一种用于气冷微堆的候选国产细颗粒核石墨设计了5种强度试验，即德标单向拉伸、美标三点弯折、美标巴西圆盘劈裂拉伸、美标单向压缩和美标单向拉伸强度试验，对其强度概率分布进行了系统的实验研究。研究发现，二参数Weibull分布对5种强度试验数据的拟合结果均通过了Anderson-Darling检验（A-D检验），而且相比正态分布和三参数Weibull分布，该分布的拟合结果在低概率下更加保守，这说明采用二参数Weibull分布描述本文研究的国产细颗粒核石墨的强度概率分布是合适的。该核石墨特征强度与应力状态及应力梯度密切相关，单向压缩强度远高于单向拉伸强度，而后者明显高于巴西圆盘劈裂拉伸强度，三点弯折强度显著高于单向拉伸强度。Weibull模数（体现了强度的分散性）与应力状态密切相关，单向拉伸应力状态下的强度分散性远高于单向压缩应力状态，而巴西圆盘内高应力危险区域（应力达到中心最大值的90%以上区域）应力状态介于单向拉伸与单向压缩之间，其强度分散性也介于二者之间，这说明应该将Weibull模数视为应力状态的函数。
-
关键词:
- 核石墨 /
- 强度 /
- 概率分布 /
- Weibull分布 /
- Anderson-Darling检验
Abstract: Five strength tests are conducted for a candidate domestic fine-grained nuclear graphite used in gas-cooled micro-reactors, including the uniaxial tensile test as per the standard of Deutsche Industrie Norm (DIN), as well as the three-point flexural test, the Brazilian disc splitting tensile test, the uniaxial compressive test, and the uniaxial tensile test as per the standards of American Society for Testing and Materials (ASTM). Based on the test results, the strength probability distributions are systematically analyzed. It was found that the fitting results of the two-parameter Weibull distribution to the five types of strength data all pass the Anderson-Darling test (A-D test). Compared to the normal distribution and the three-parameter Weibull distribution, the fitting results of the two-parameter Weibull distribution are more conservative at low probabilities. Therefore, it is reasonable to use the two-parameter Weibull distribution to describe the strength probability distribution of the domestic fine-grained graphite studied. The characteristic strength of the nuclear graphite is closely related to the stress state and gradient. The uniaxial compressive strength is much higher than the uniaxial tensile strength, while the latter is clearly higher than the Brazilian disc splitting tensile strength. The three-point flexural strength is obviously higher than the uniaxial tensile strength. In addition, the Weibull modulus, which reflects the strength dispersion, is closely related to the stress state. The strength dispersion under the uniaxial tensile stress state is much higher than that under the uniaxial compressive stress state. The strength dispersion of Brazilian disc splitting tensile strength is between the above two, because the stress state in the high-stress critical region of the Brazilian disc, where the stress reaches more than 90% of the maximum value of the center, is between the uniaxial tensile and uniaxial compressive stress states. This observation suggests that the Weibull modulus should be considered as a function of stress states.-
Key words:
- Nuclear graphite /
- Strength /
- Probability distribution /
- Weibull distribution /
- Anderson-Darling test
-
图 2 德标单向拉伸试件与夹具
Figure 2. The Uniaxial Tensile Specimen and Fixture as per the Standard of DIN
图 3 美标三点弯折试件与夹具
Figure 3. The Three-point Flexural Specimen and Fixture as per the Standard of ASTM
图 4 美标巴西圆盘劈裂拉伸试件与夹具
Figure 4. The Brazilian Disc Splitting Tensile Specimen and Fixture as per the Standard of ASTM
图 5 美标单向拉伸试件与夹具
Figure 5. The Uniaxial Tensile Specimen and Fixture as per the Standard of ASTM
图 6 采用3种分布函数分别对于5种强度累积概率数据的拟合结果
Figure 6. Fitting Results of 3 Distribution Functions to Cumulative Probability Data from 5 Strength Tests
表 1 国产细颗粒核石墨5种强度试验所测强度数据的统计结果
Table 1. Statistical Results of Strength Data Measured in 5 Strength Tests on the Domestic Fine-grained Nuclear Graphite
强度试验类型 试验数量/个 强度均值/MPa 强度标准差/MPa 分散度（标准差/均值） 最大强度值/MPa 最小强度值/MPa 德标单向拉伸 70 28.91 2.72 0.0941 34.59 22.09 美标三点弯折 120 40.33 3.91 0.0970 47.46 26.47 美标巴西圆盘劈裂拉伸 200 24.33 1.45 0.0596 27.37 19.85 美标单向压缩 67 88.85 3.93 0.0442 97.33 80.69 美标单向拉伸 19 26.83 2.02 0.0753 29.44 23.27 
下载: 导出CSV
表 2 分别基于5种强度累积概率数据对3种分布函数的参数估计结果
Table 2. Parameter Estimation Results of 3 Distribution Functions Based on Cumulative Probability Data from 5 Strength Tests
强度试验类型 二参数
Weibull分布三参数
Weibull分布正态
分布$ m $ $ {S_{\text{c}}} $ $ m' $ $ S_{\text{0}}' $ $ S_{\text{c}}' $ $ \varSigma $ $ {\mu ^{}} $ 德标单向拉伸 12.25 29.90 12.25 0.03 29.90 2.72 28.91 美标三点弯折 12.66 42.04 12.66 0.01 42.09 3.90 40.33 美标巴西圆盘劈裂拉伸 19.86 24.98 19.86 0.04 25.00 1.45 24.33 美标单向压缩 24.51 90.43 5.79 67.53 90.47 3.93 88.85 美标单向拉伸 12.50 27.84 12.44 0.01 27.84 2.07 26.83
下载: 导出CSV
表 3 3种累积概率分布对5种试验强度-累积概率数据集的拟合优度检验结果
Table 3. Goodness-of-Fit Test Results of 3 Cumulative Probability Distributions for 5 Experimental Strength-Cumulative Probability Datasets
累积概率分布 A-D检验统计量 德标单向拉伸 美标三点弯折 美标巴西圆盘劈裂拉伸 美标单向压缩 美标单向拉伸 二参数Weibull分布 $ {A^2} $ 0.8086 0.3222 0.3360 0.3193 0.9379 $ p $ 0.5138 0.5243 0.5046 0.5268 0.0519 是否通过检验 通过 通过 通过 通过 通过 三参数Weibull分布 $ {A^2} $ 0.8010 0.3220 0.3334 0.1923 0.9376 $ p $ 0.5223 0.5249 0.5079 0.8922 0.0521 是否通过检验 通过 通过 通过 通过 通过 正态分布 $ {A^2} $ 0.3801 1.3879 2.1028 0.2683 0.6759 $ p $ 0.3942 0.0012 0.0000 0.6730 0.0615 是否通过检验 通过 未通过 未通过 通过 通过
下载: 导出CSV
-
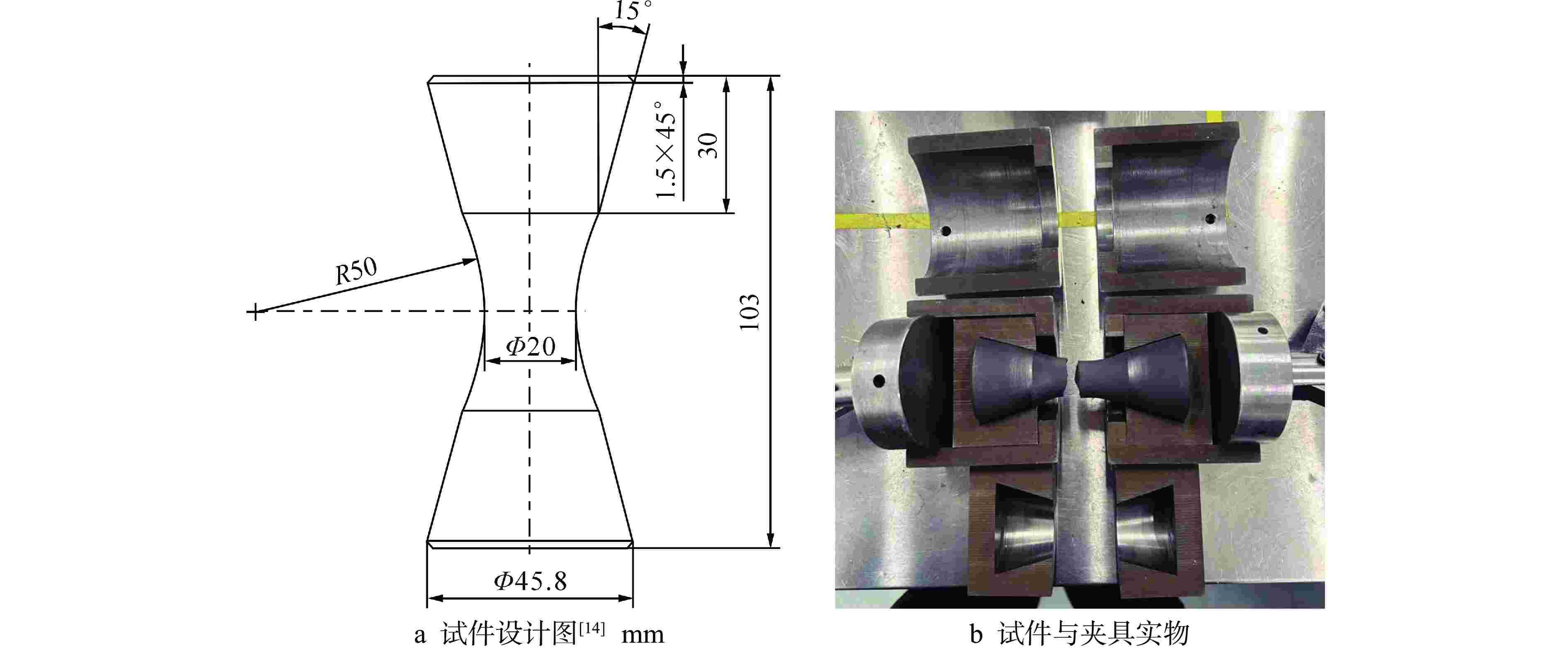
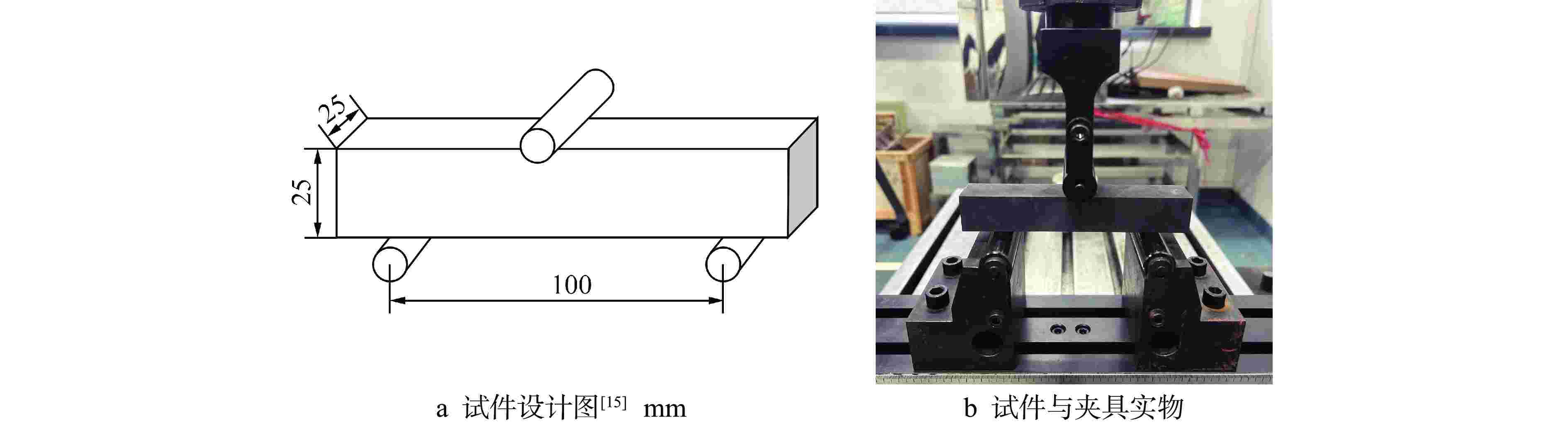
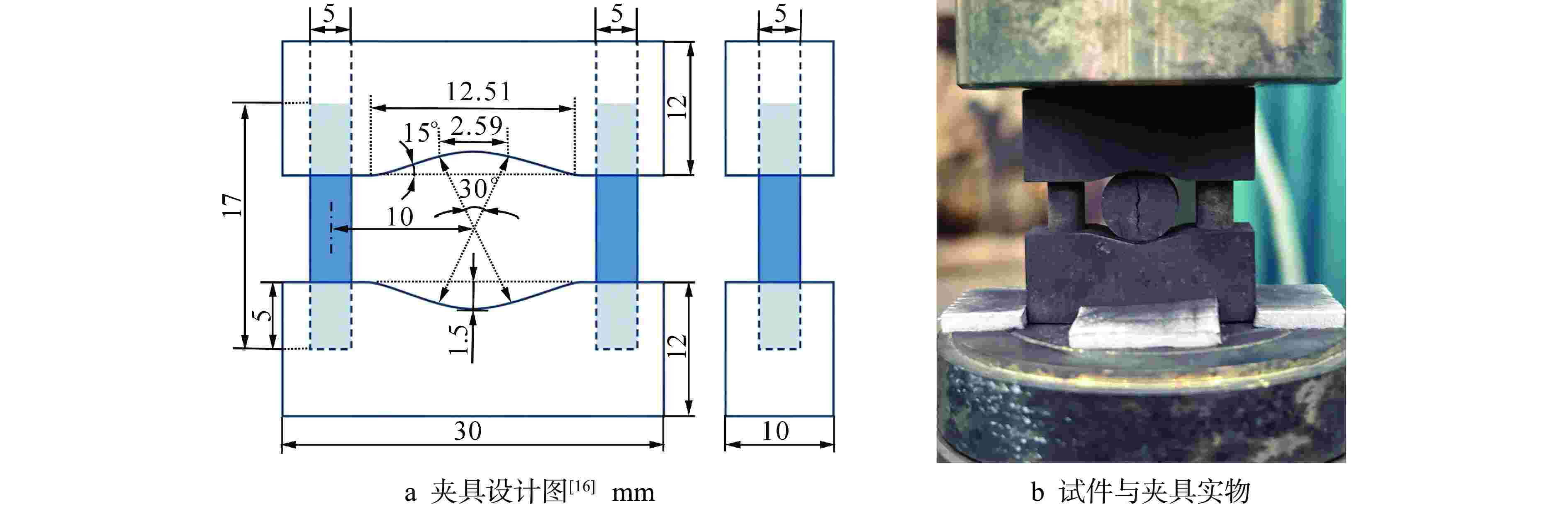
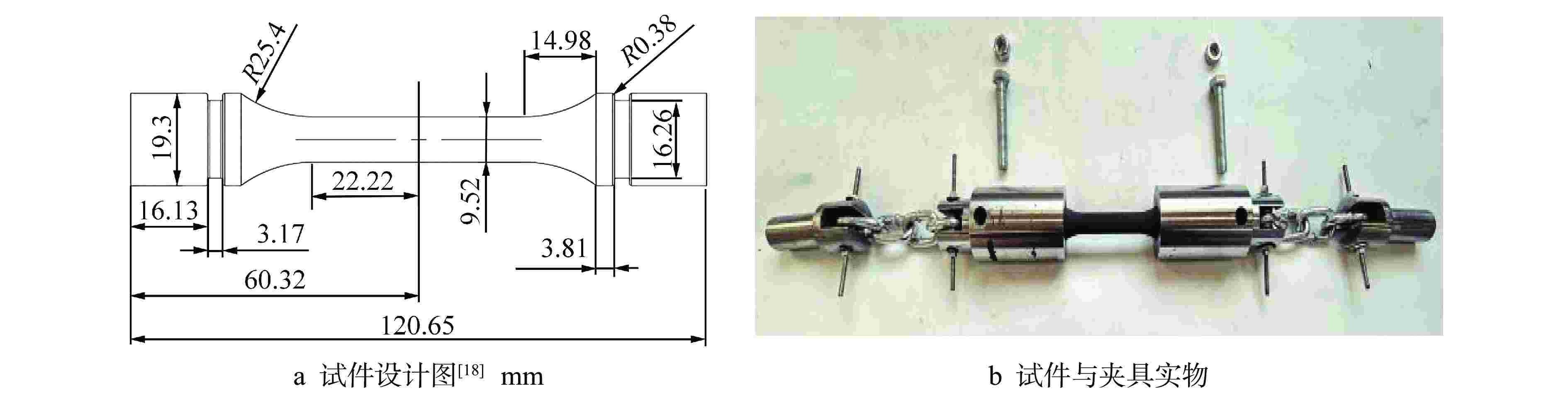
[1] 王泓杰, 史力, 王晓欣, 等. ASME规范概率评价方法对细颗粒石墨的适用性研究[J]. 原子能科学技术, 2017, 51(12): 2306-2311. doi: 10.7538/yzk.2017.51.12.2306 [2] 王泓杰, 史力, 王晓欣, 等. 针对细颗粒石墨的改进概率评价方法研究[J]. 原子能科学技术, 2017, 51(9): 1611-1616. doi: 10.7538/yzk.2017.51.09.1611 [3] 丁冬, 高彦涛, 杨雄, 等. 基于ASME规范的核石墨改进概率评价方法研究[J]. 核技术, 2019, 42(1): 85-90. [4] HINDLEY M P, MITCHELL M N, BLAINE D C, et al. Observations in the statistical analysis of NBG-18 nuclear graphite strength tests[J]. Journal of Nuclear Materials, 2012, 420(1-3): 110-115. doi: 10.1016/j.jnucmat.2011.09.013 [5] PRICE R J. Statistical study of the strength of near-isotropic graphite: GA-A-13955[R]. San Diego: General Atomic Corporation, 1976. [6] 王泓杰, 史力, 王晓欣, 等. IG-110石墨强度分布与失效概率研究[J]. 核动力工程, 2017, 38(3): 56-60. [7] 亢方亮, 孙立斌, 于溯源, 等. 3种国产高温气冷堆核石墨拉伸强度实验研究[C]//第15届全国反应堆结构力学大会. 北京: 中国核学会, 2008: 553-559. [8] 胡玉琴, 孙立斌, 王洪涛, 等. 高温气冷堆工程验证用国产石墨的强度实验研究[J]. 科技导报, 2012, 30(21): 45-50. doi: 10.3981/j.issn.1000-7857.2012.21.006 [9] 田冬青, 史力, 孙立斌, 等. 基于巴西圆盘试验的国产石墨拉伸强度及特性研究[J]. 原子能科学技术, 2023, 57(3): 591-599. doi: 10.7538/yzk.2022.youxian.0202 [10] SUN X M, DONG Y J, ZHOU Y P, et al. Effects of reaction temperature and inlet oxidizing gas flow rate on IG-110 graphite oxidation used in HTR-PM[J]. Journal of Nuclear Science and Technology, 2017, 54(2): 196-204. doi: 10.1080/00223131.2016.1233080 [11] ZHAN G B, KONISHI T. Relationship between the Toyo Tanso Group and HTR-PM[C]. Beijing: Tsinghua University, 2014: 3-6. [12] KTA. HTR ceramic pressure for vessels internals: KTA - 3232[S]. Germany: Nuclear Safety Standards Commission, 1992: 7-10. [13] ASME. Boiler and Pressure Vessel Code ASME III Division 5: High Temperature Reactors: ASME BPVC.III-2023[S]. USA:ASME, 2023: 462-470. [14] DIN.Testing of carbonaceous materials-Determination of tensile strength-Solid materials: DIN 51914-2009[S]. Berlin: DIN, 2009: 3-8. [15] ASTM International. Test method for flexural strength of manufactured carbon and graphite articles using three-point loading at room temperature: ASTM D7972-14[S]. USA: ASTM International, 2014: 1-4. [16] ASTM International. Standard test method for tensile strength estimate by disc compression of manufactured graphite: ASTM D8289-20[S]. USA: ASTM International, 2020: 1-5. [17] ASTM International. Standard test method for compressive strength of carbon and graphite: ASTM C695-21[S]. USA: ASTM International, 2021: 1-3. [18] ASTM International. Standard test method for tensile stress-strain of carbon and graphite: ASTM C749-15(2020)[S]. USA: ASTM International, 2020: 1-9. [19] LE CAM L. Maximum likelihood: an introduction[J]. International Statistical Review/Revue Internationale de Statistique, 1990, 58(2): 153-171. [20] MIODRAG LOVRIC. International Encyclopedia of Statistical Science[M]. Berlin: Springer, 2011: 52-54. [21] Nemeth N N, Bratton R L. Statistical models of fracture relevant to nuclear-grade graphite: review and recommendations: E-16798-1[R]. Cleveland: NASA, 2011: 12-24. -
下载:
计量
- 文章访问数: 17
- HTML全文浏览量: 3
- PDF下载量: 0
- 被引次数: 0
