Analysis of Primary Loop System of High-Order Fully-Implicit Nuclear Reactor Based on MOOSE Platform
-
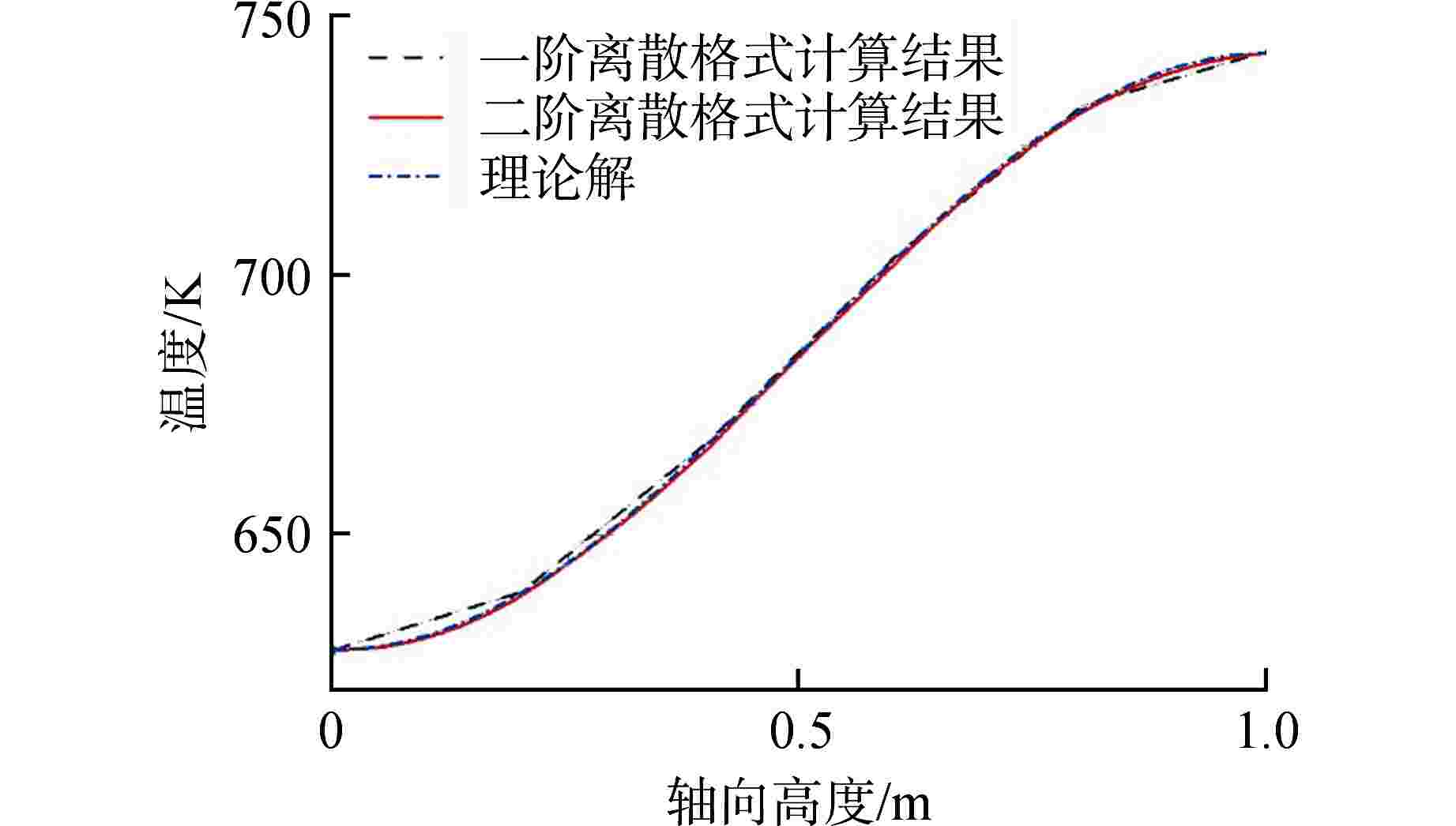
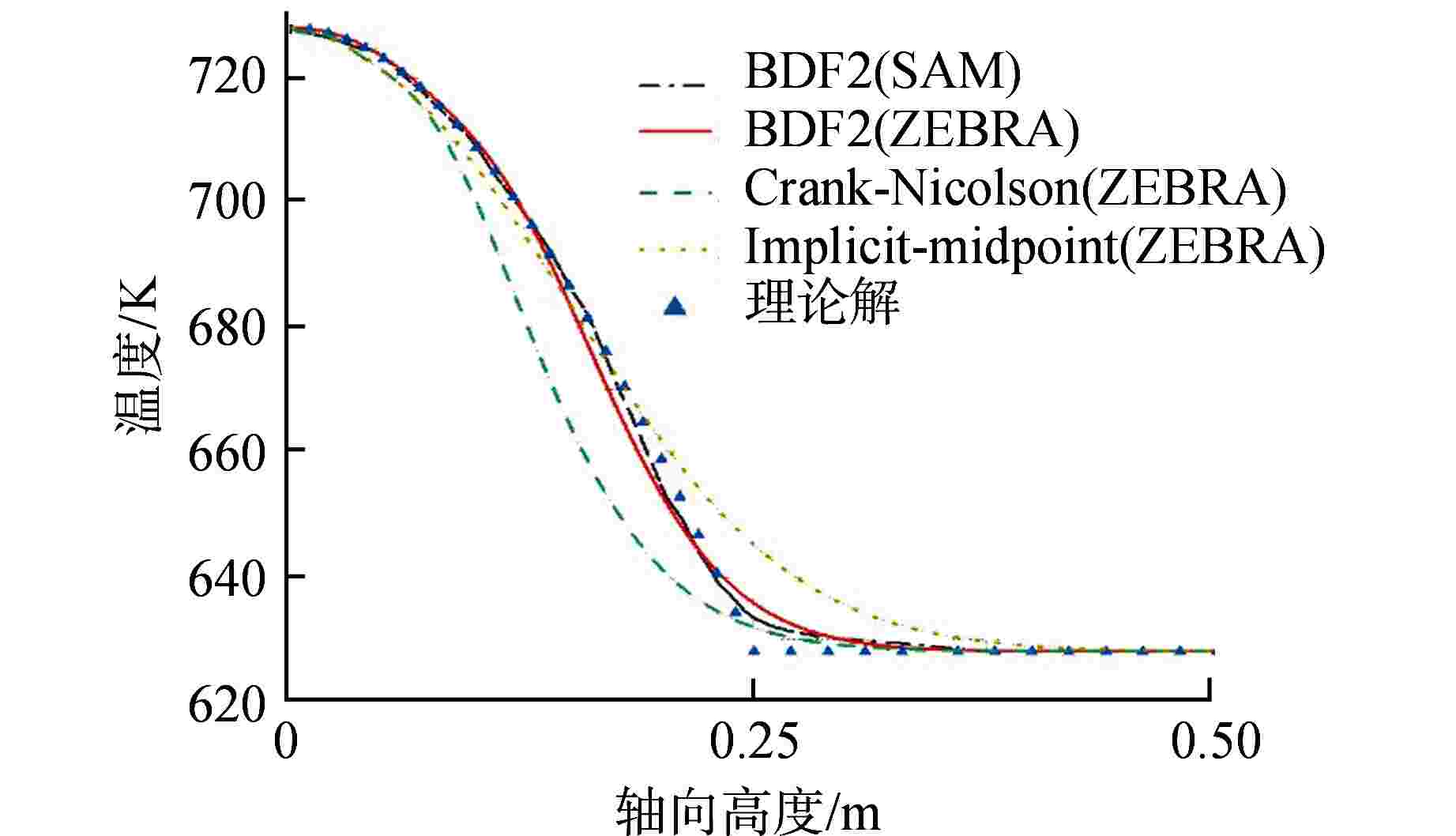
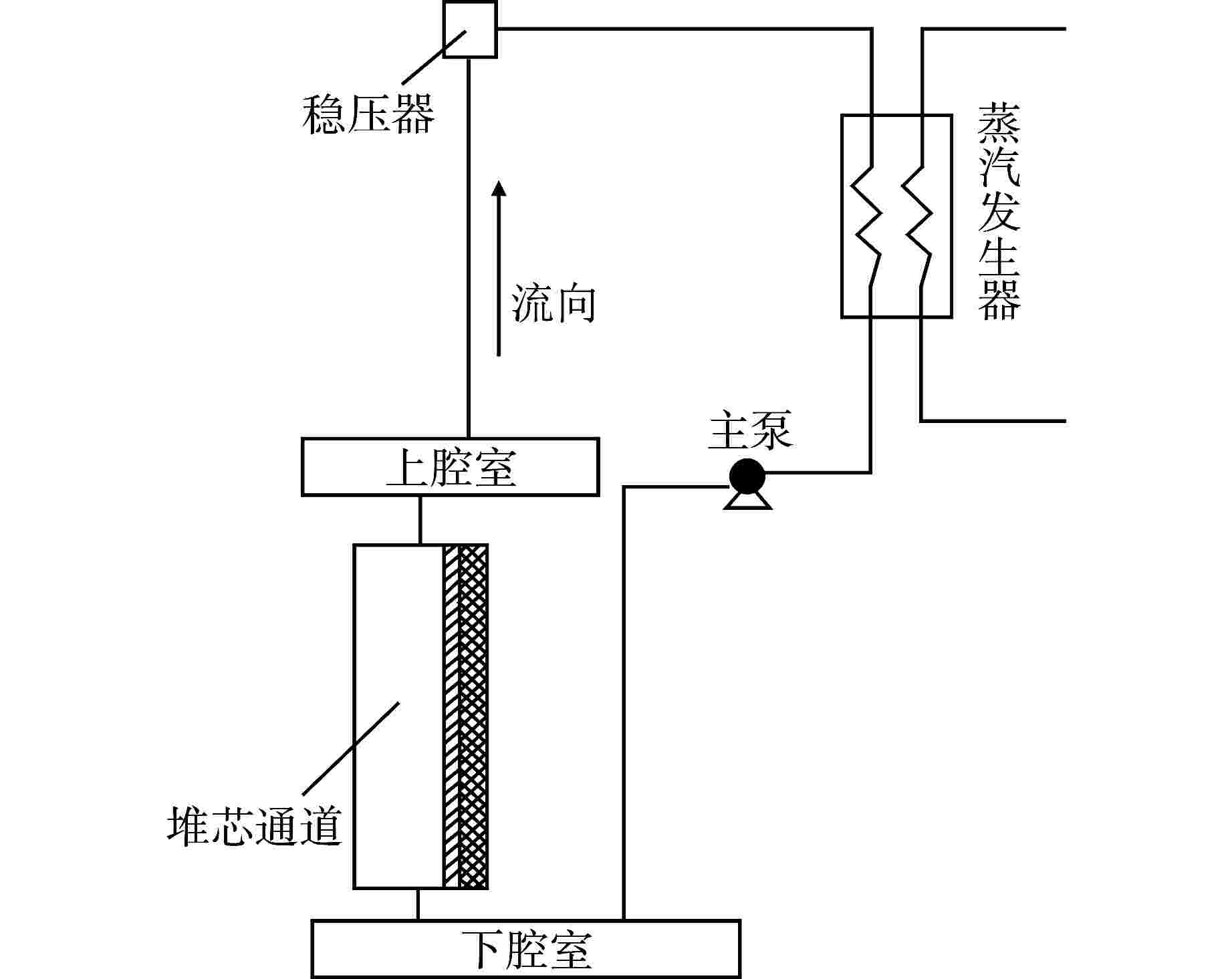
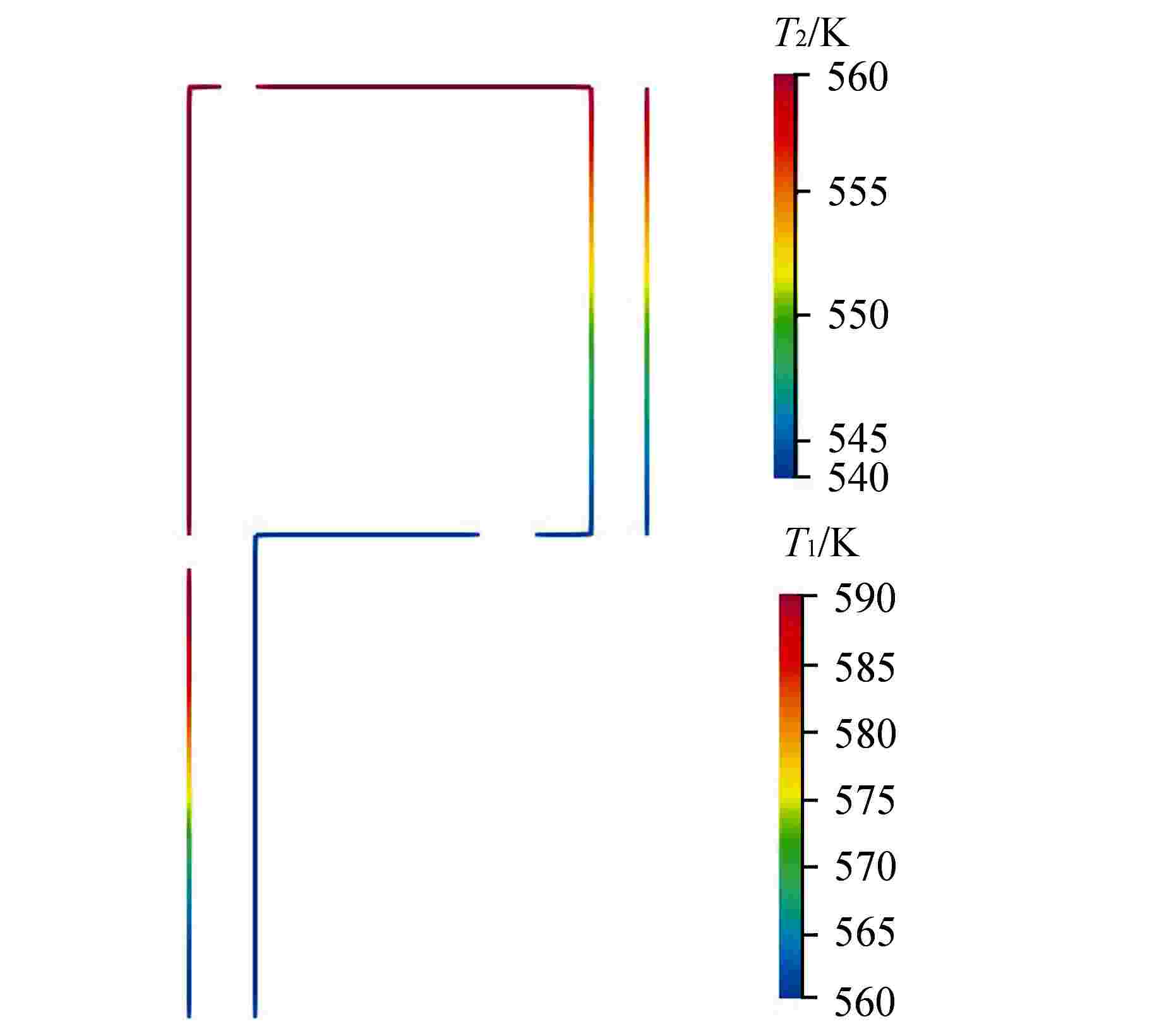
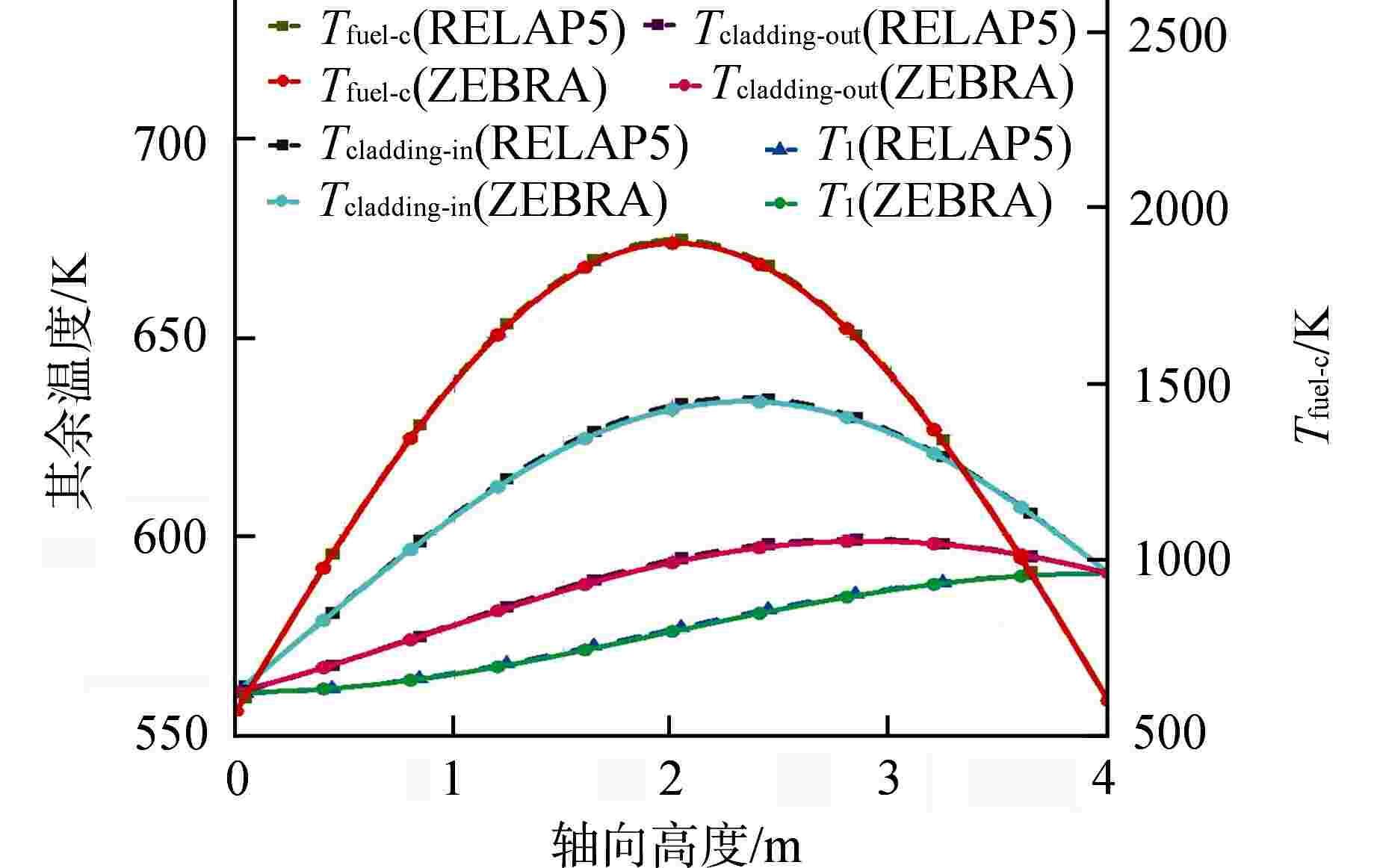
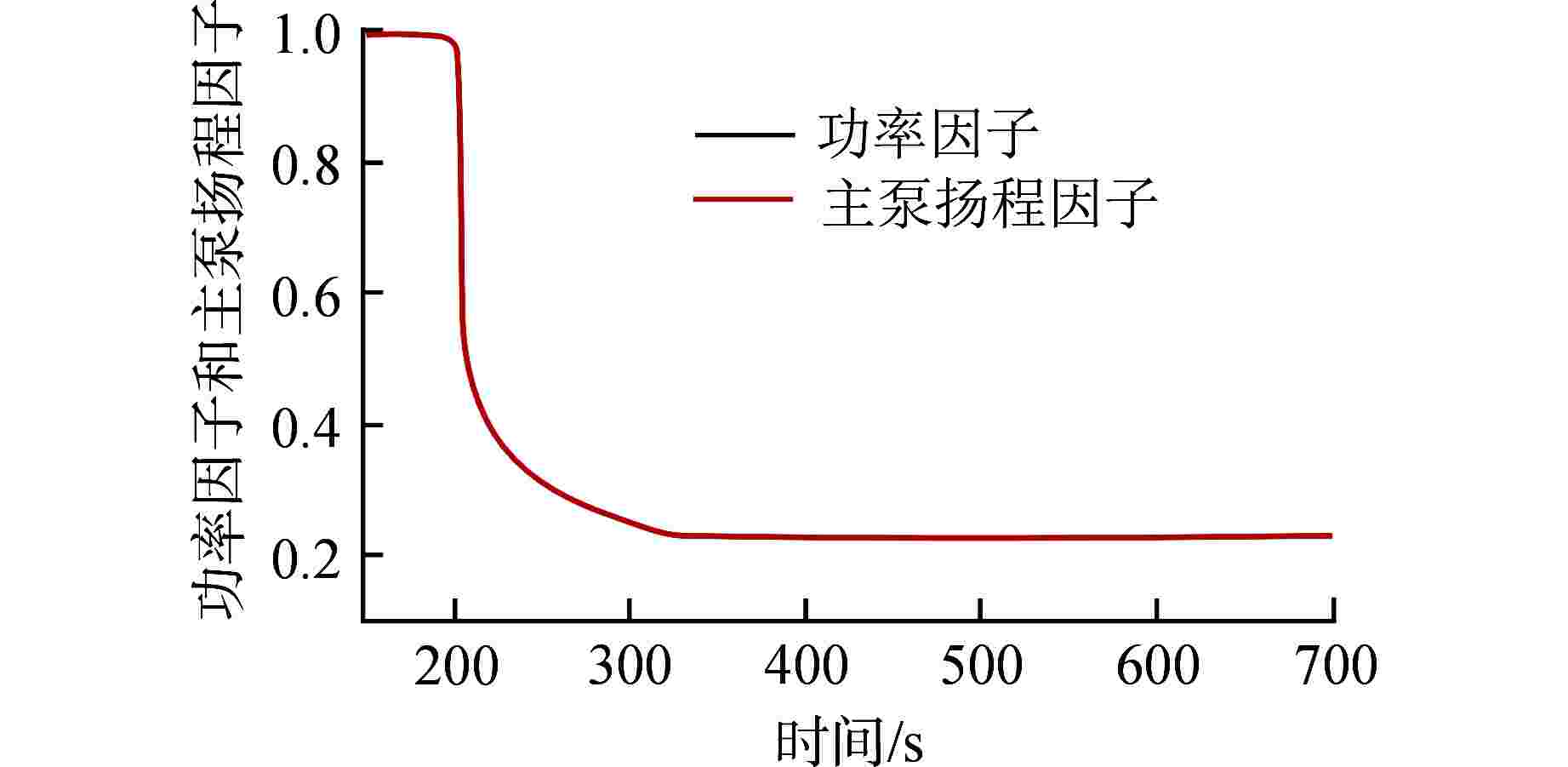
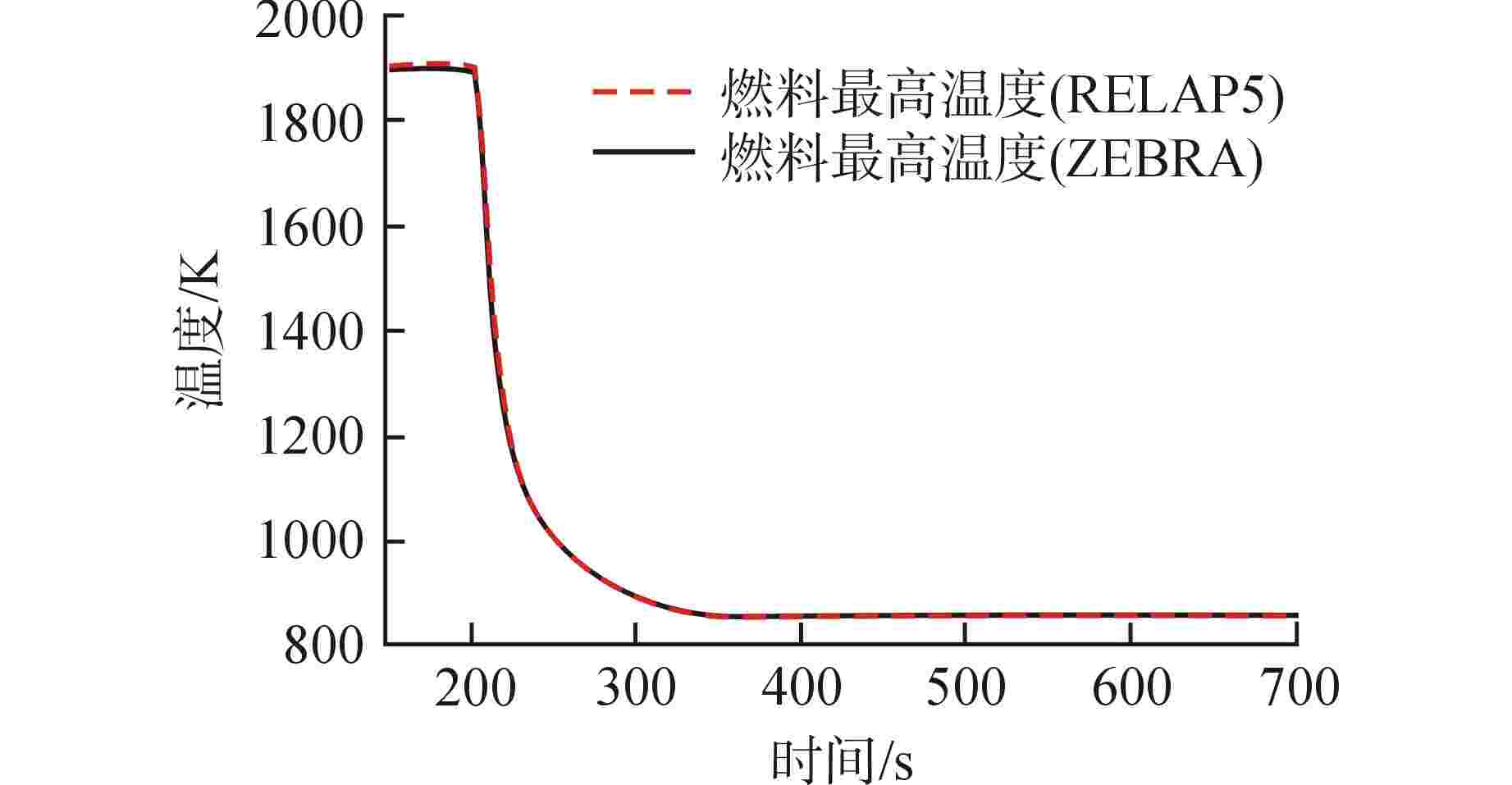
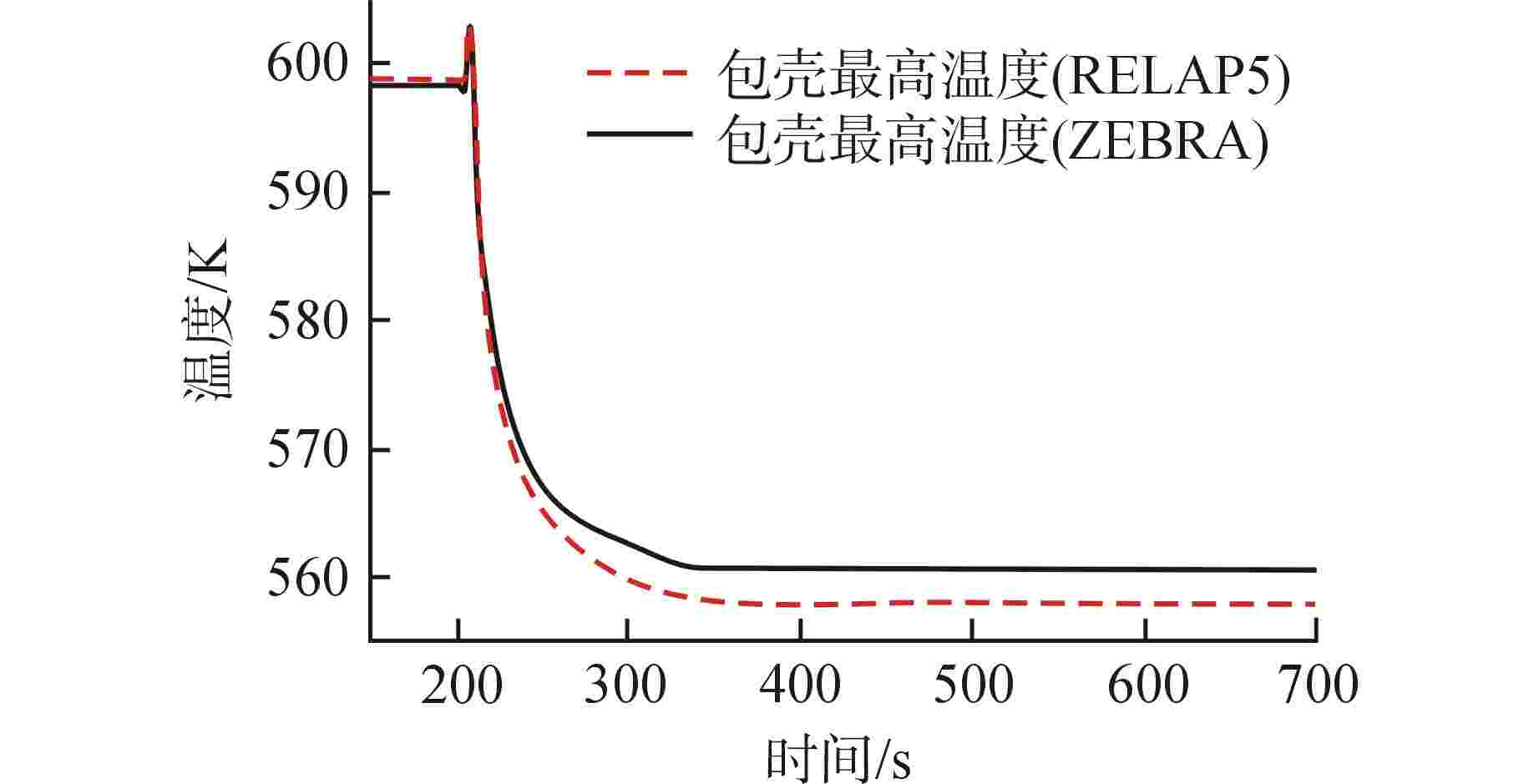
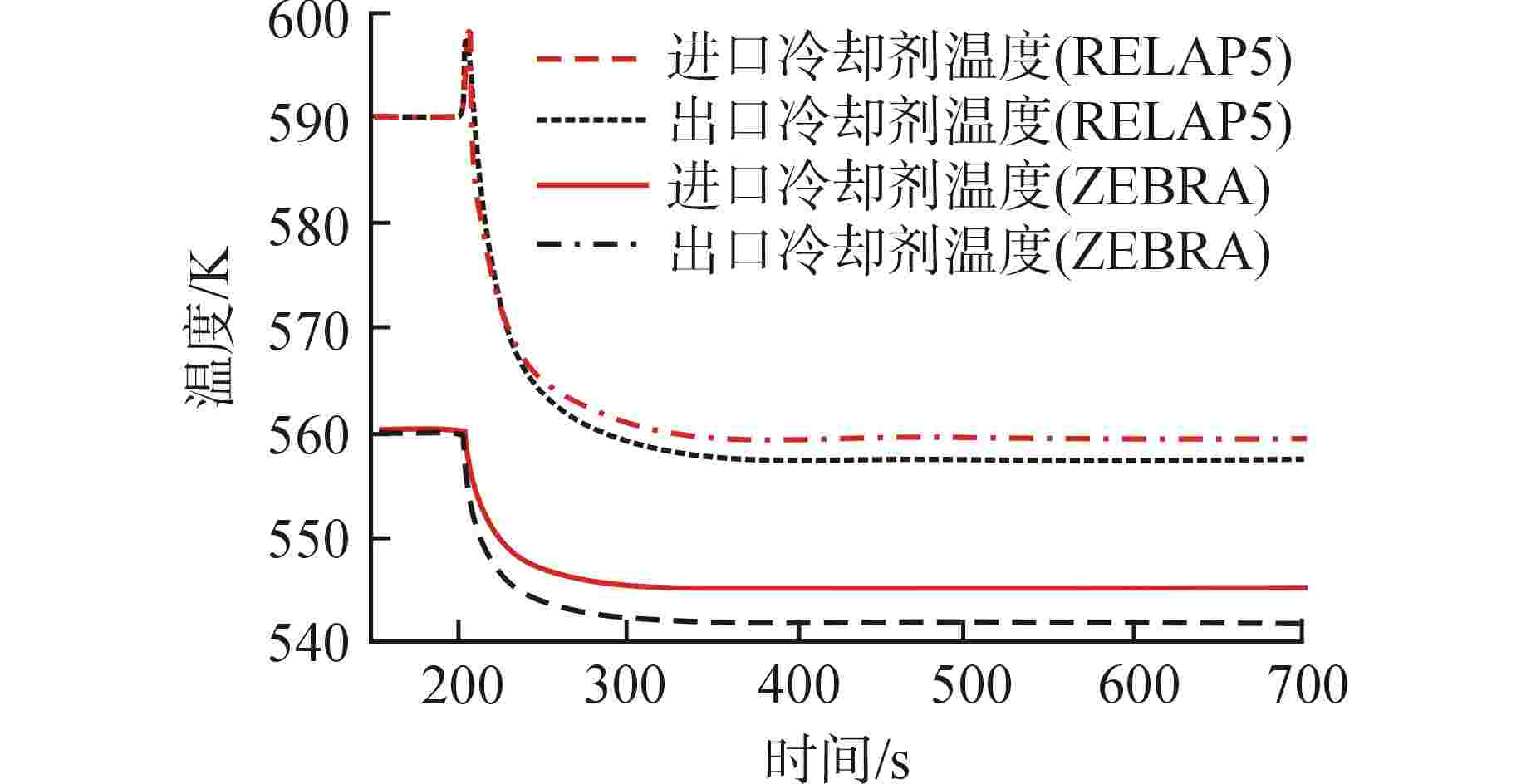
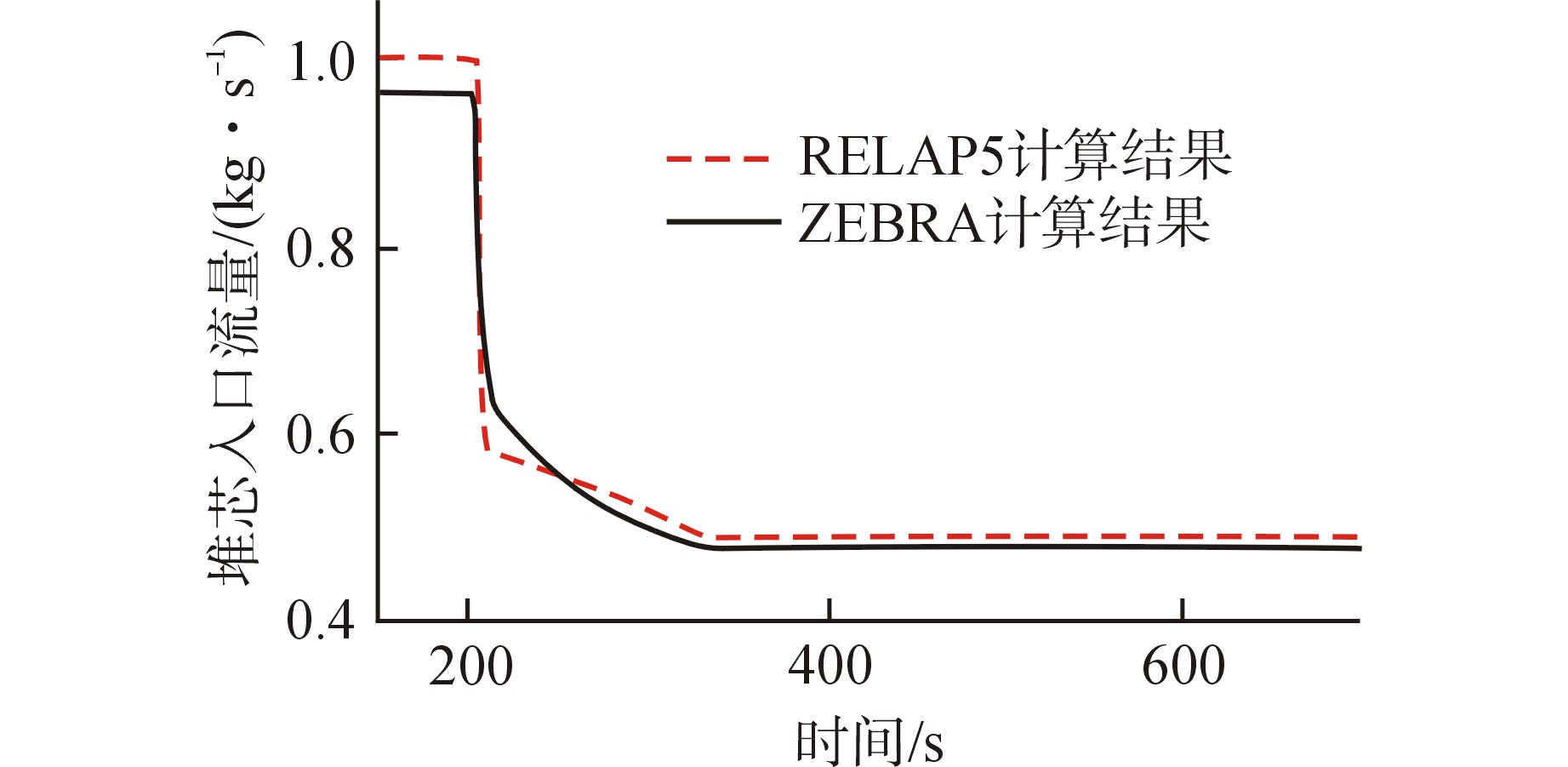
摘要: 基于多物理场耦合平台MOOSE开发了模块化系统安全分析程序ZEBRA，并采用高阶全隐式离散格式建立了核反应堆一回路系统模型，对核反应堆系统中子扩散、二维固体导热和一维流体进行耦合计算。针对单管流动传热问题，对ZEBRA程序进行了耦合验证，对比了稳态工况下一阶、二阶空间离散格式和瞬态工况下Implicit-Euler、Crank-Nicolson、BDF2 这3种时间离散格式的求解精度，并对压水堆回路系统稳态和降功率瞬态工况进行了模拟分析。结果表明，高阶空间离散格式具有较高的求解精度，BDF2时间离散格式与理论解符合最好；压水堆回路系统温度、速度、压力分布合理，稳态、瞬态计算结果与RELAP5程序计算结果符合良好。Abstract: Based on the multi-physics coupling platform MOOSE (Multiphysics Object Oriented Simulation Environment), the modular system safety analysis code, ZEBRA, was developed. The high-order and fully-implicit discrete format was presented to establish the nuclear reactor primary loop model. And the coupling calculation of nuclear reactor system including neutron diffusion, two-dimensional solid heat conduction, and one-dimensional fluid were also implemented. For the problem of flow and heat transfer in a single pipe, the ZEBRA code is coupled and verified, and the solution accuracy of first-order and second-order spatial discrete formats under steady-state conditions and Implicit-Euler, Crank-Nicolson and BDF2 schemes under transient conditions are compared, and the steady-state and power-reducing transient conditions of PWR loop system are simulated and analyzed. The results show that the high-order spatial discrete format has a higher accuracy, and the BDF2 time discrete format is in best agreement with the theoretical solution. The temperature, velocity, and pressure distribution of the PWR loop system are reasonable. The steady-state and transient calculation results are in good agreement with those of RELAP5.
-
Key words:
- MOOSE /
- High-Order fully-implicit /
- System analysis
-
图 2 ZEBRA稳态单管温度对比验证
Figure 2. Temperature Comparison and Verification of Single Pipe in ZEBRA Steady State
图 3 0.5 s时各离散格式下沿轴向温度分布对比验证
Figure 3. Comparison and Verification of Axial Temperature Distributions under Various Discrete Formats at 0.5 s
图 4 压水堆单相回路计算对象示意图
Figure 4. Schematic Diagram of Computing Object of Single-Phase Loop in PWR
图 8 强迫循环单相回路节点图
118—一次侧；140—二次侧；其余节点与图4中部件对应
Figure 8. Node Diagram of Single-Phase Loop with Forced Circulation
图 9 稳态工况ZEBRA与RELAP5燃料各位置温度对比
Figure 9. Comparison of Temperature at Various Positions of Fuel between ZEBRA and RELAP5 under Steady-state Conditions
图 10 功率因子和主泵扬程因子随时间的变化
Figure 10. Changes of Power Factor and Main Pump Head Factor over Time
图 11 瞬态燃料最高温度对比
Figure 11. Comparison of the Maximum Fuel Temperature in Transient Condition
图 12 瞬态包壳最高温度对比
Figure 12. Comparison of the Maximum Fuel Cladding Temperature in Transient Condition
图 13 瞬态堆芯进、出口冷却剂温度对比
Figure 13. Comparison of Inlet and Outlet Coolant Temperature of Reactor Core in Transient Condition
图 14 瞬态堆芯进口流量对比
Figure 14. Comparison of the Inlet Flow Rate of Reactor Core in Transient Condition
表 1 单管部件稳态几何参数和边界条件
Table 1. Geometric Parameters and Boundary Conditions of Single-pipe Component Under Steady State
参数名 参数值 管道直径/m 0.02 长度/m 1 通流面积/m2 0.000341 热源/(W·m−3) 108sin(πz) 进口速度/(m·s−1) 0.5 进口温度/K 628 出口压力/Pa 2×105 摩擦因子 0.017 
下载: 导出CSV
表 2 单相回路几何参数和边界条件
Table 2. Geometric Parameters and Boundary Conditions of Single-Phase Loop
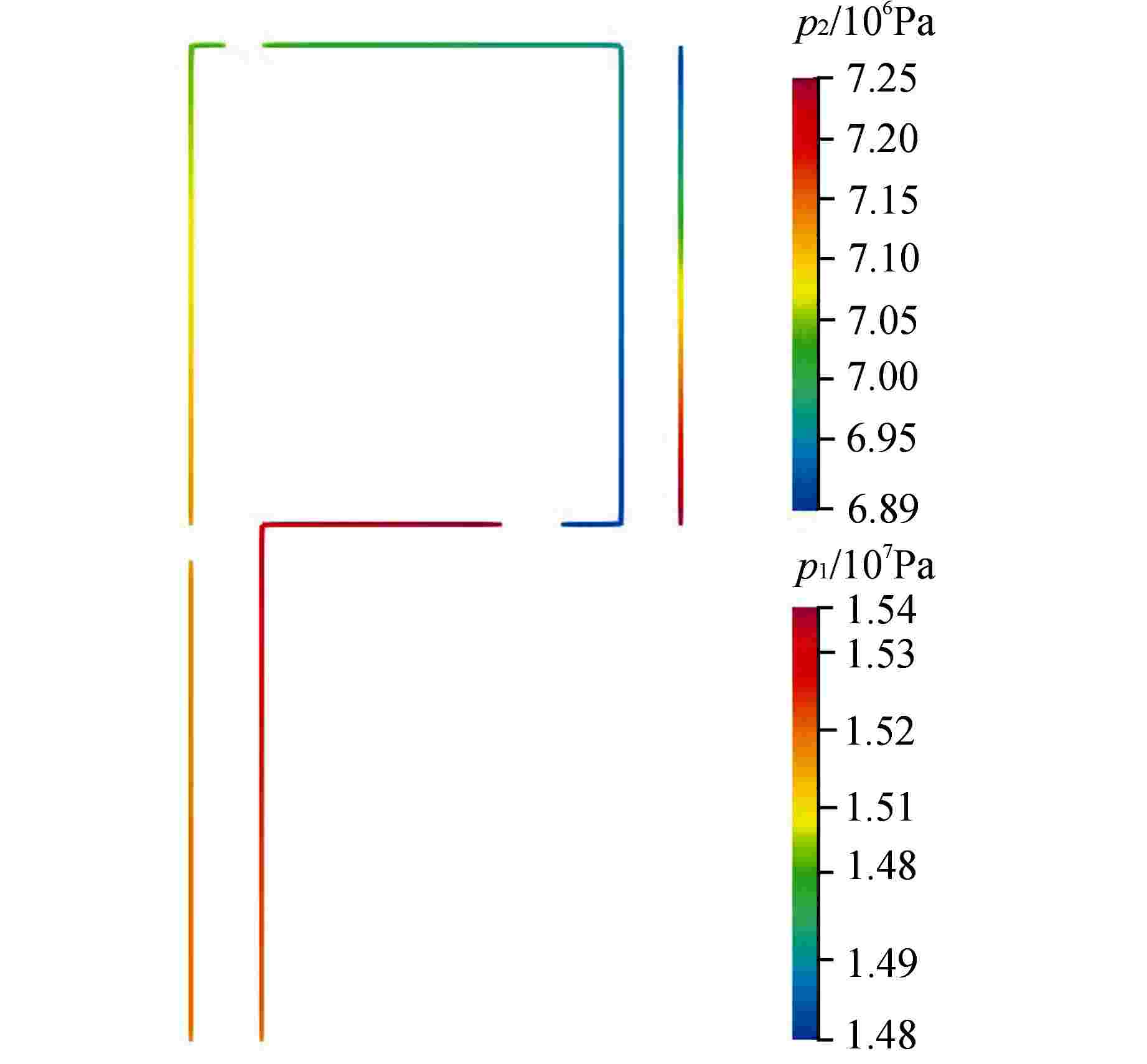
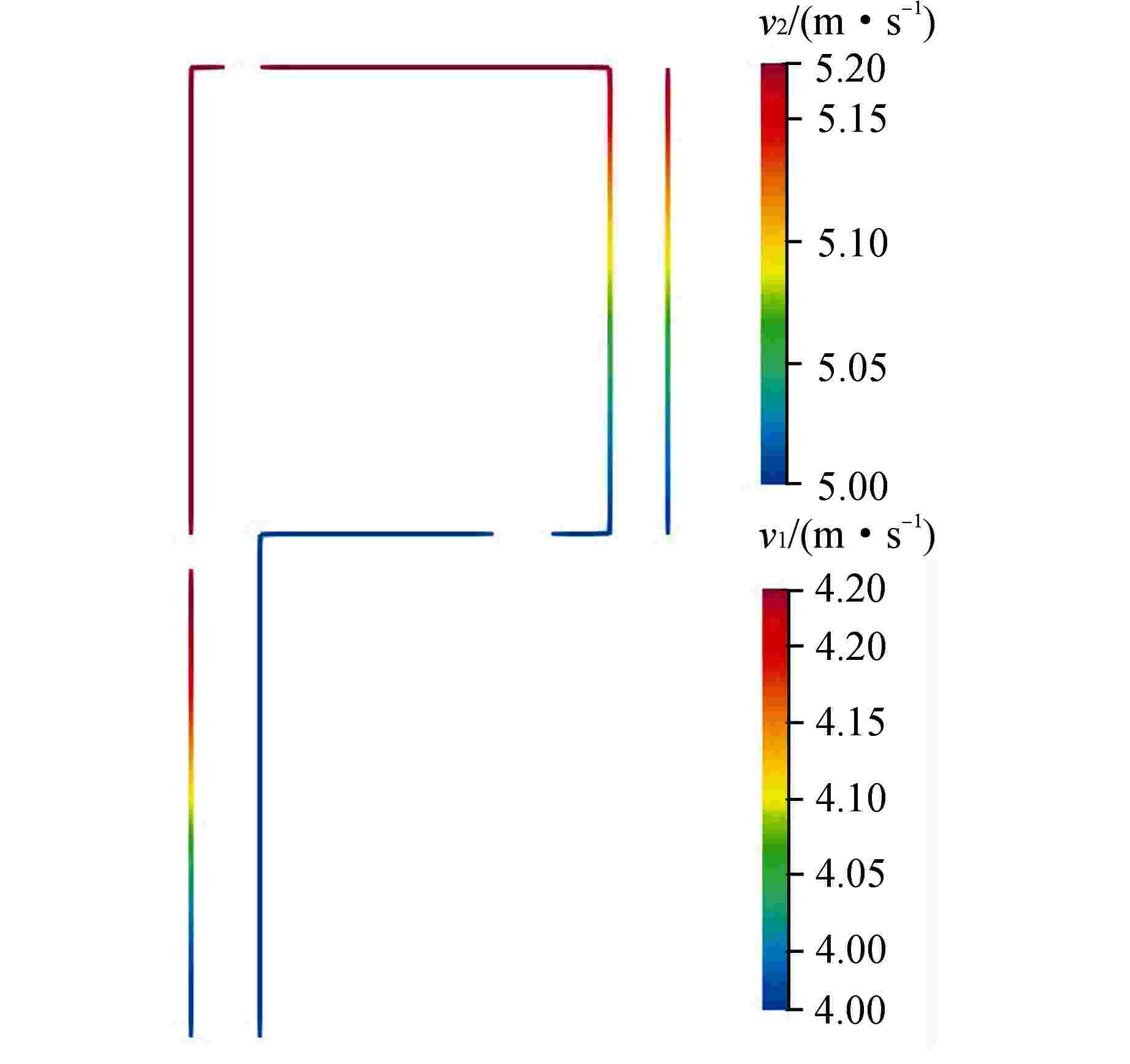
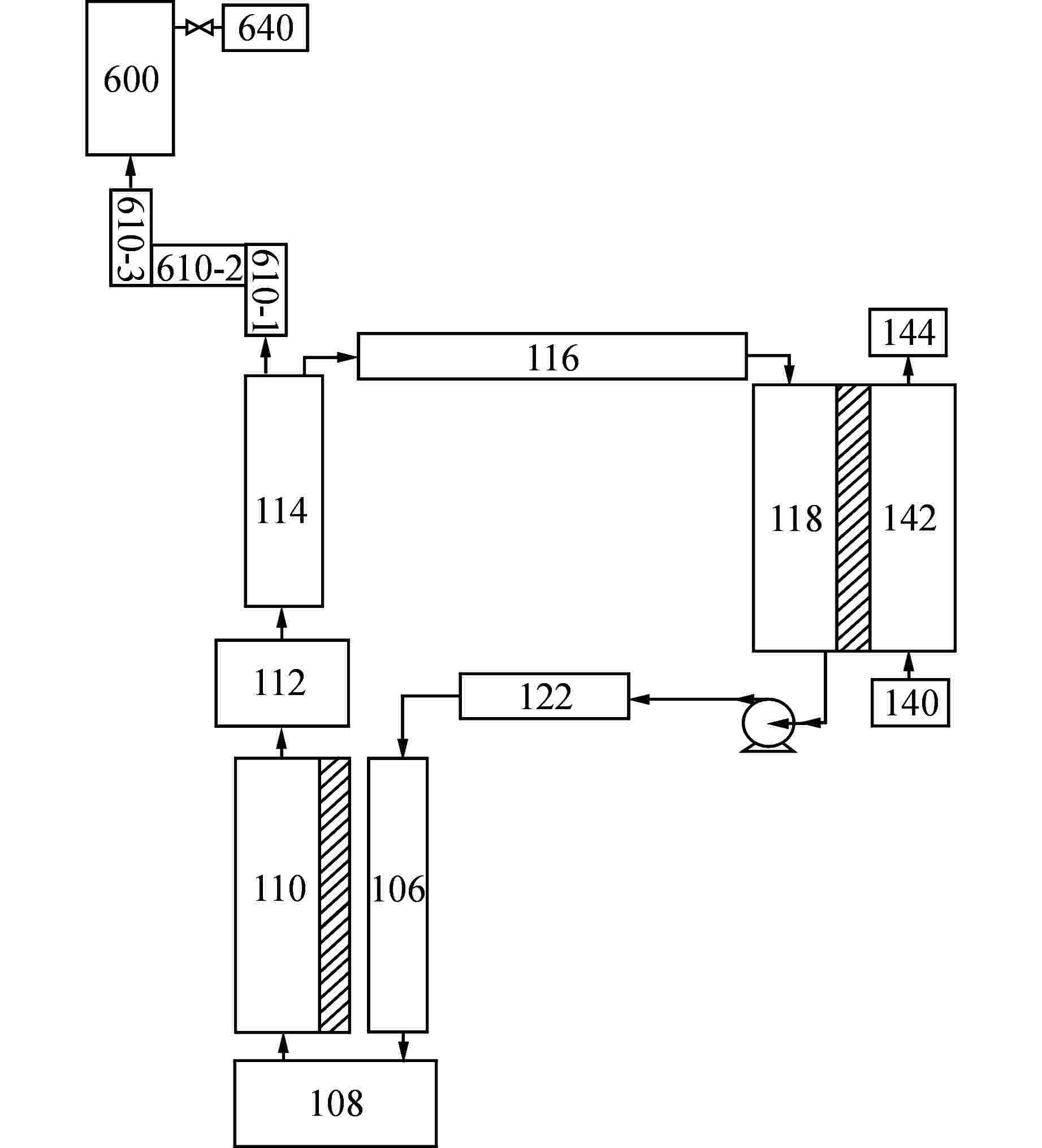
参数名 参数值 堆芯通道长度/m 3.66 湿周/m 321.341 通流面积/m2 1.161864 燃料总功率/MW 0.1 燃料芯块直径/cm 0.9391 气隙厚度/cm 0.00955 燃料包壳厚度/cm 0.0673 热交换器高度/m 4 一、二次侧湿周/m 2695.1 一、二次侧通流面积/m2 5 固体壁面高度/m 4 固体壁面厚度/mm 1 一、二次侧阻力系数 0.01 初始流速/(m·s−1) 5 初始温度/K 560 初始压力/MPa 15.17 二次侧入口流速/(m·s−1) 5 二次侧入口温度/K 484 二次侧出口压力/MPa 6.89 初始keff 2
下载: 导出CSV
-
[1] Nuclear Regulatory Commission. RELAP5/MOD3 code manual. Volume 4, Models and correlations[R]. Washington, U. S. : Nuclear Regulatory Commission, 1995. [2] GEFFRAYE G, ANTONI O, FARVACQUE M, et al. CATHARE 2 V2.5_2: a single version for various applications[J]. Nuclear Engineering and Design, 2011, 241(11): 4456-4463. doi: 10.1016/j.nucengdes.2010.09.019 [3] ZOU L, PETERSON J, ZHAO H H, et al. Solving implicit multi-mesh flow and conjugate heat transfer problems with RELAP-7[C]//Proceedings of 2013 International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering. Sun Valley, Idaho: American Nuclear Society, 2013. [4] HU R, YU Y Q. A computationally efficient method for full-core conjugate heat transfer modeling of sodium fast reactors[J]. Nuclear Engineering and Design, 2016(308): 182-193. doi: 10.1016/j.nucengdes.2016.08.018 [5] LINDSAY A, HUFF K. Moltres: finite element based simulation of molten salt reactors[J]. The Journal of Open Source Software, 2018, 3(21): 298. doi: 10.21105/joss.00298 [6] GASTON D, NEWMAN C, HANSEN G, et al. MOOSE: a parallel computational framework for coupled systems of nonlinear equations[J]. Nuclear Engineering and Design, 2009, 239(10): 1768-1778. doi: 10.1016/j.nucengdes.2009.05.021 [7] WANG Y Q, SCHUNERT S, DEHART M, et al. Hybrid PN-SN with Lagrange multiplier and upwinding for the multiscale transport capability in Rattlesnake[J]. Progress in Nuclear Energy, 2017(101): 381-393. doi: 10.1016/j.pnucene.2017.03.020 [8] DEHART M, GLEICHER F, ORTENSI J, et al. Multi-Physics simulation of TREAT kinetics using MAMMOTH[C]//Proceedings of 2015 ANS Winter Meeting. Washington: Idaho National Lab., 2015: 1187-1190. [9] WILLIAMSON R L, HALES J D, NOVASCONE S R, et al. Multidimensional multiphysics simulation of nuclear fuel behavior[J]. Journal of Nuclear Materials, 2012, 423(1-3): 149-163. doi: 10.1016/j.jnucmat.2012.01.012 [10] HE Y N, CHEN P, WU Y W, et al. Preliminary evaluation of U3Si2-FeCrAl fuel performance in light water reactors through a multi-physics coupled way[J]. Nuclear Engineering and Design, 2018(328): 27-35. doi: 10.1016/j.nucengdes.2017.12.019 [11] 邓超群, 向烽瑞, 贺亚男, 等. 基于MOOSE平台的棒状燃料元件性能瞬态分析程序开发与验证[J/OL]. 原子能科学技术. [2021-02-01]. https: //kns. cnki. net/kcms/detail/11.2044. tl. 20210129.1308. 010. html. [12] HU R. A fully-implicit high-order system thermal-hydraulics model for advanced non-LWR safety analyses[J]. Annals of Nuclear Energy, 2017(101): 174-181. doi: 10.1016/j.anucene.2016.11.004 [13] OLSHANSKII M A. A low order Galerkin finite element method for the Navier–Stokes equations of steady incompressible flow: a stabilization issue and iterative methods[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(47-48): 5515-5536. doi: 10.1016/S0045-7825(02)00513-3 [14] HU R. Preliminary SAM assessment: ANL/NE-17/4[R]. Argonne, United States: Argonne National Lab (ANL), 2018. [15] IVANOV K N, BEAM T M, BARATTA A J. Pressurised water reactor main steam line break (MSLB) benchmark: NEA/NSC/DOC (99)8[R]. Parsipanny: US Nuclear Regulatory Commission, OECD Nuclear Energy Agency, 1999. -
下载:
计量
- 文章访问数: 848
- HTML全文浏览量: 199
- PDF下载量: 62
- 被引次数: 0
