Analysis of Factors Influencing the Accuracy of 3-D Flux Synthesis in Nuclear Reactor Primary Shielding
-
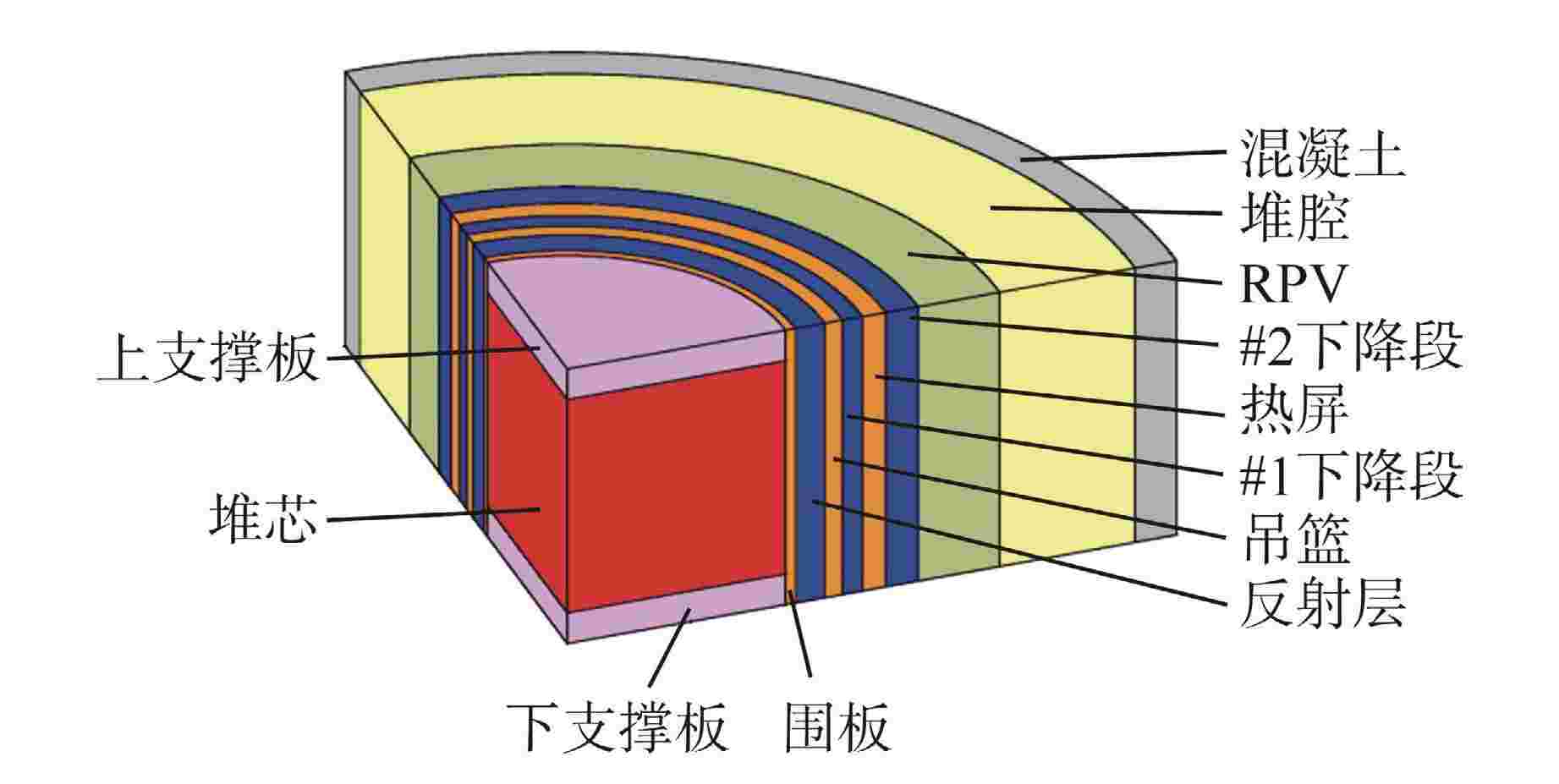
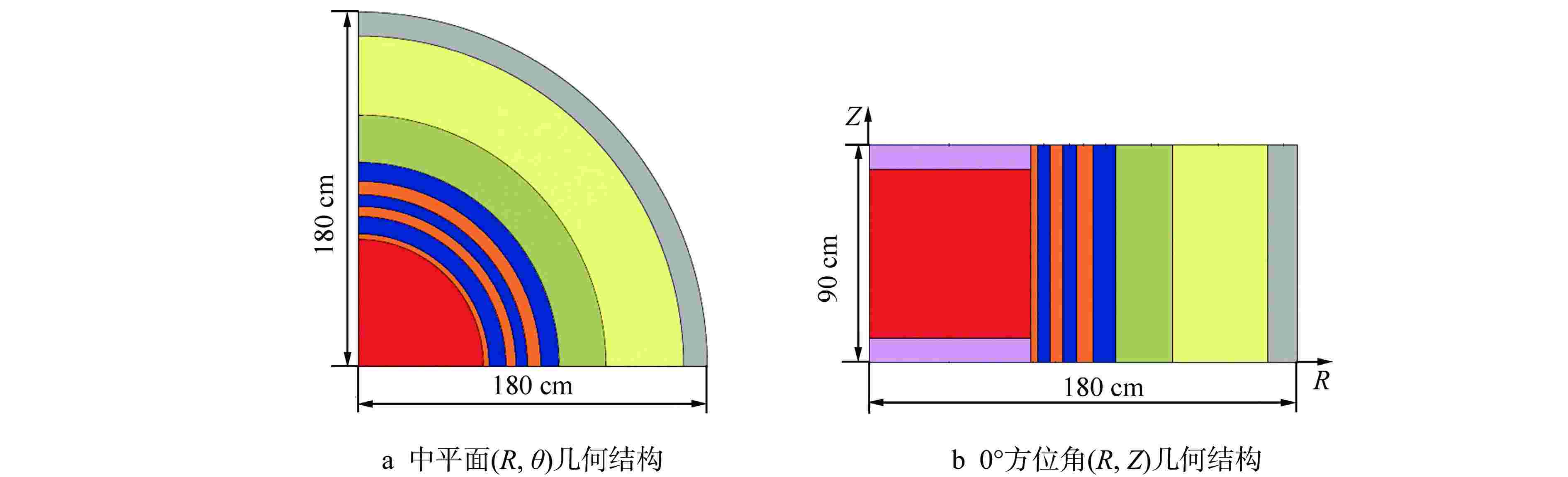
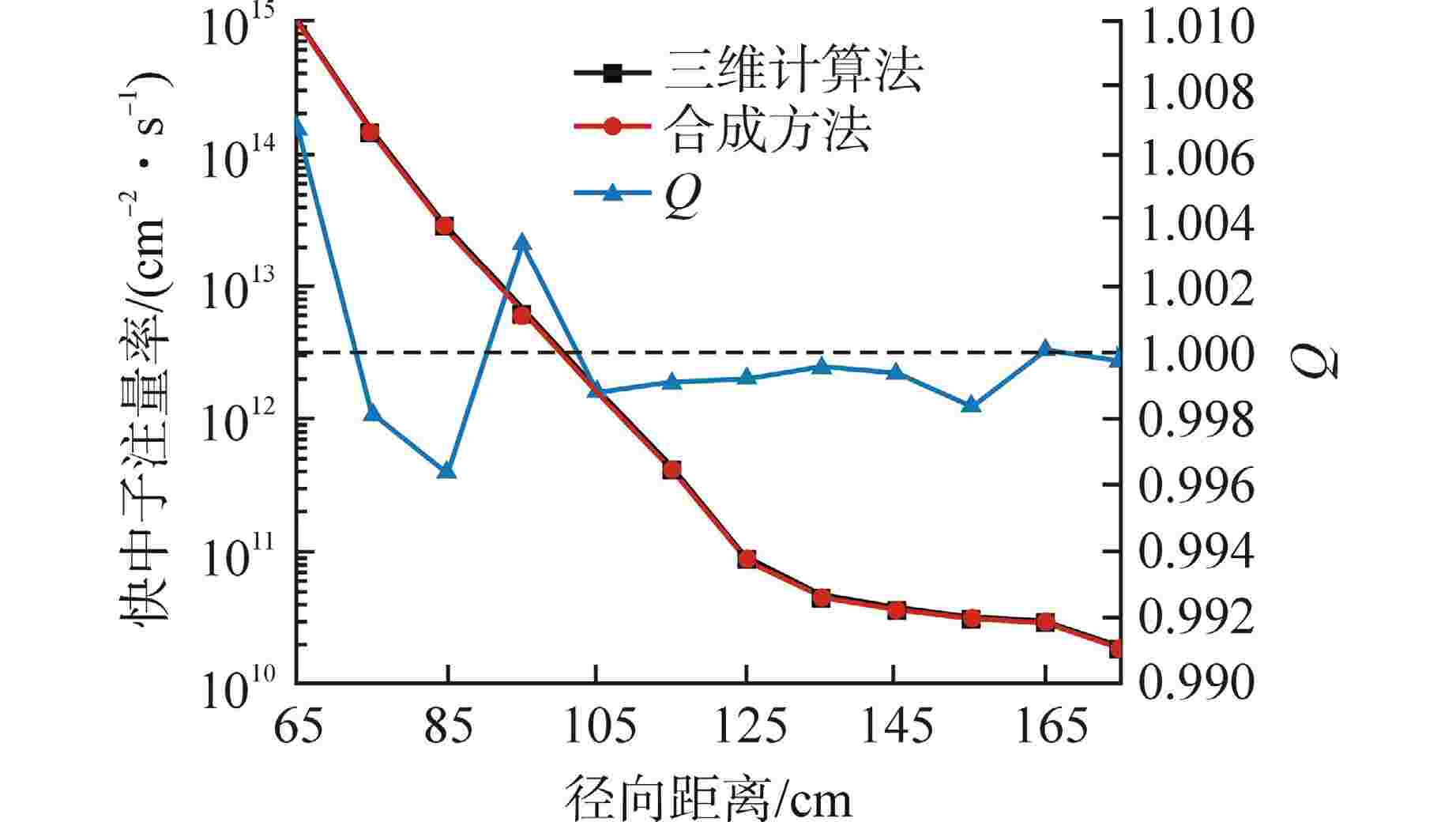
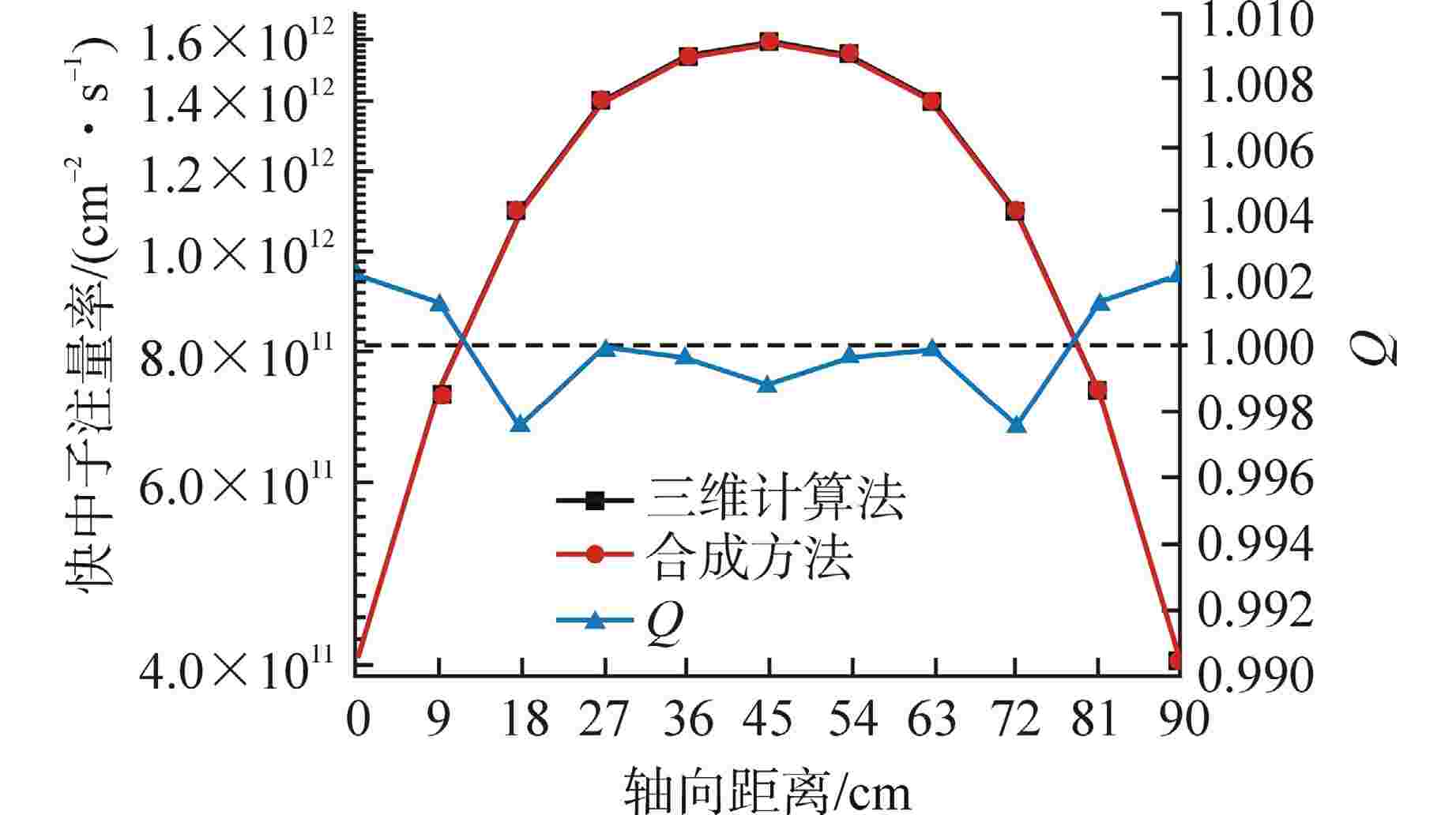
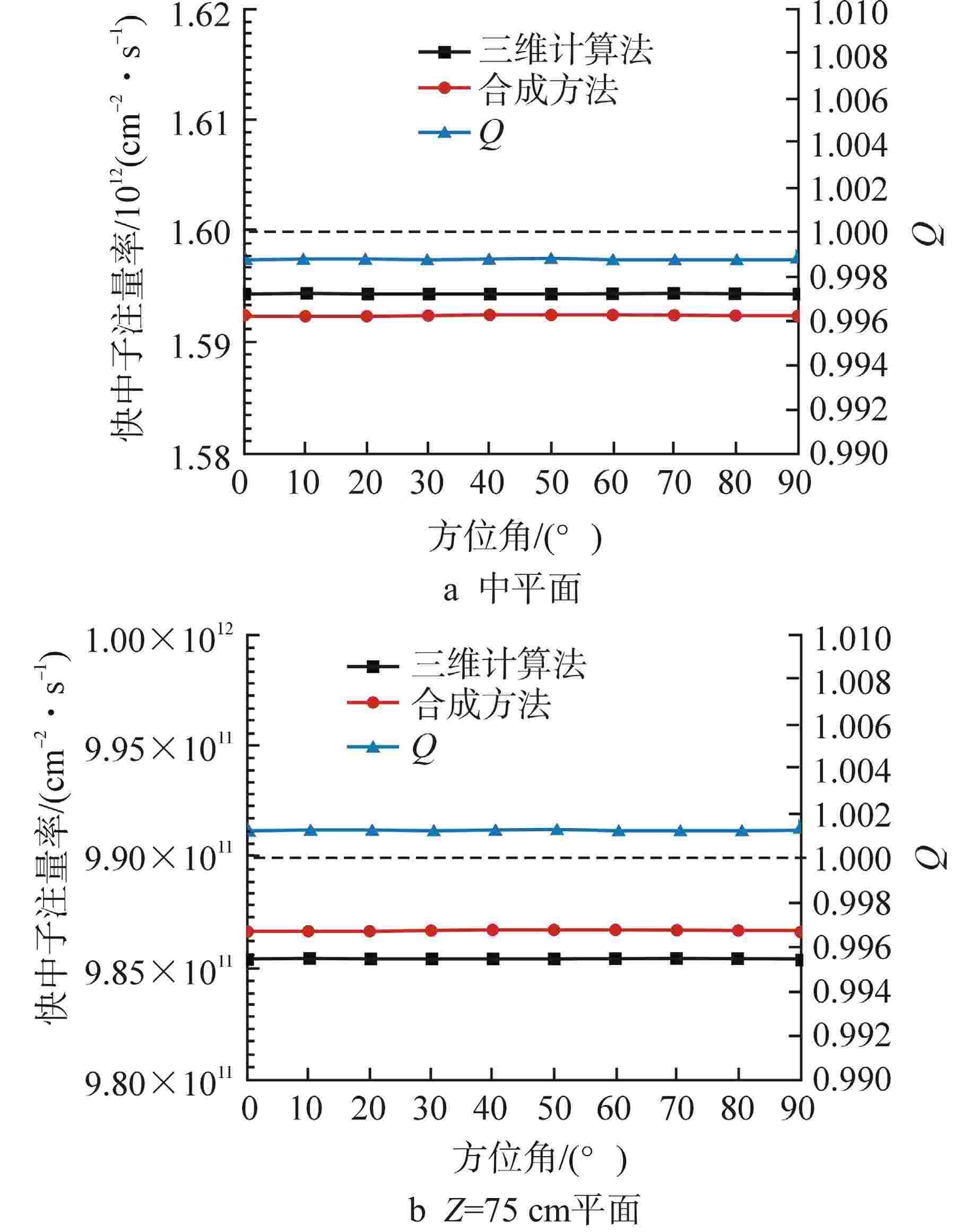
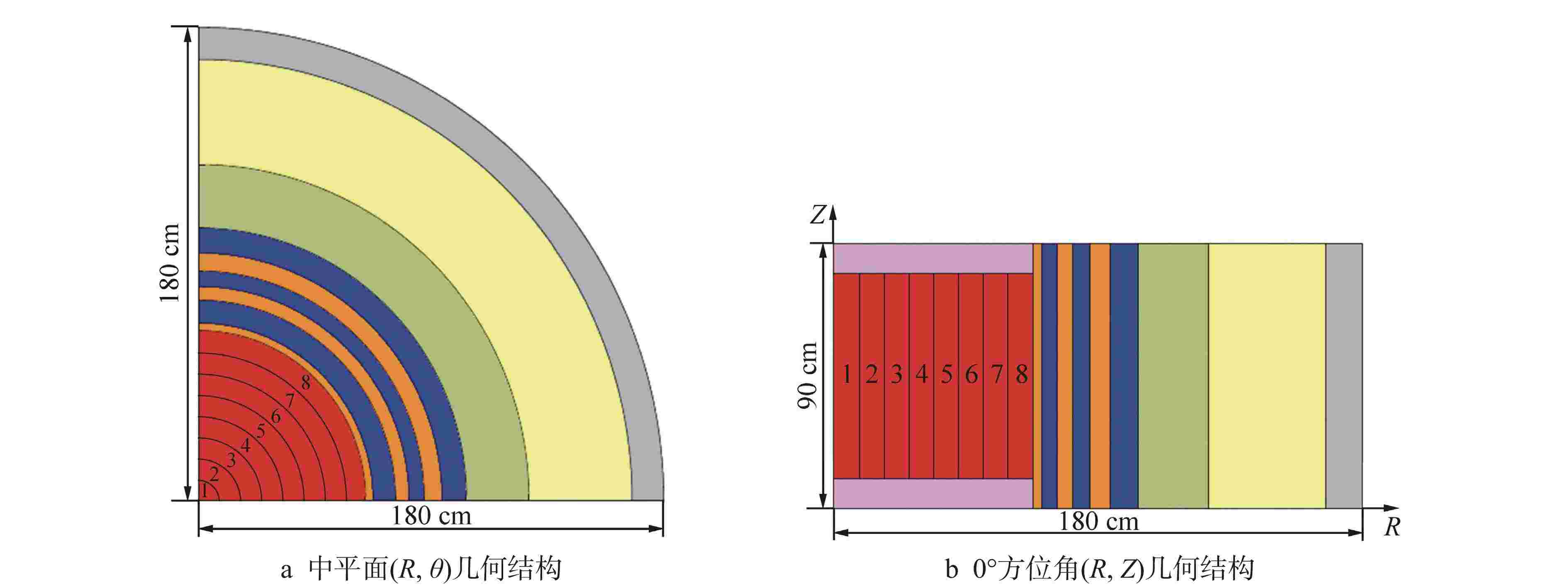
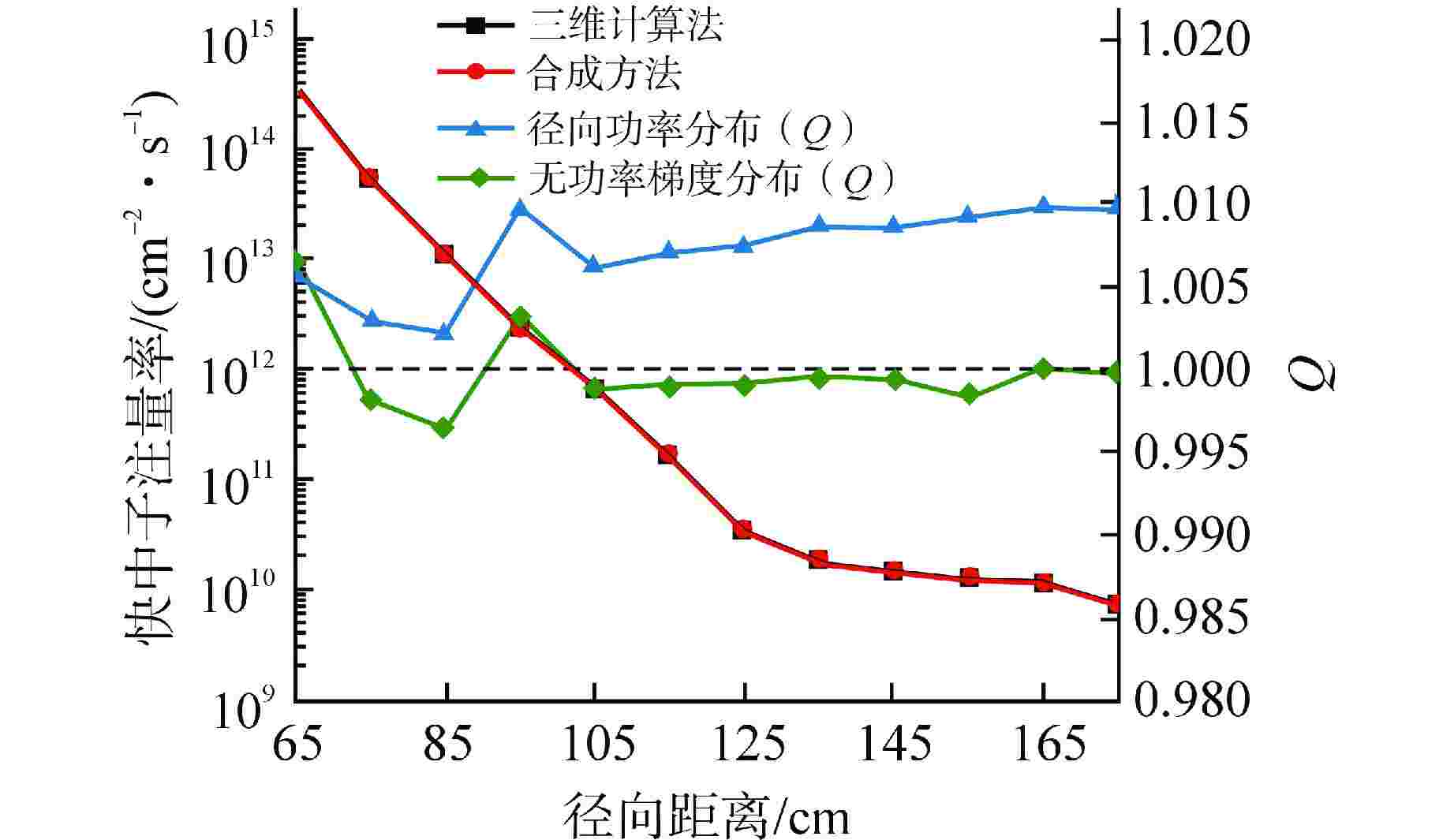
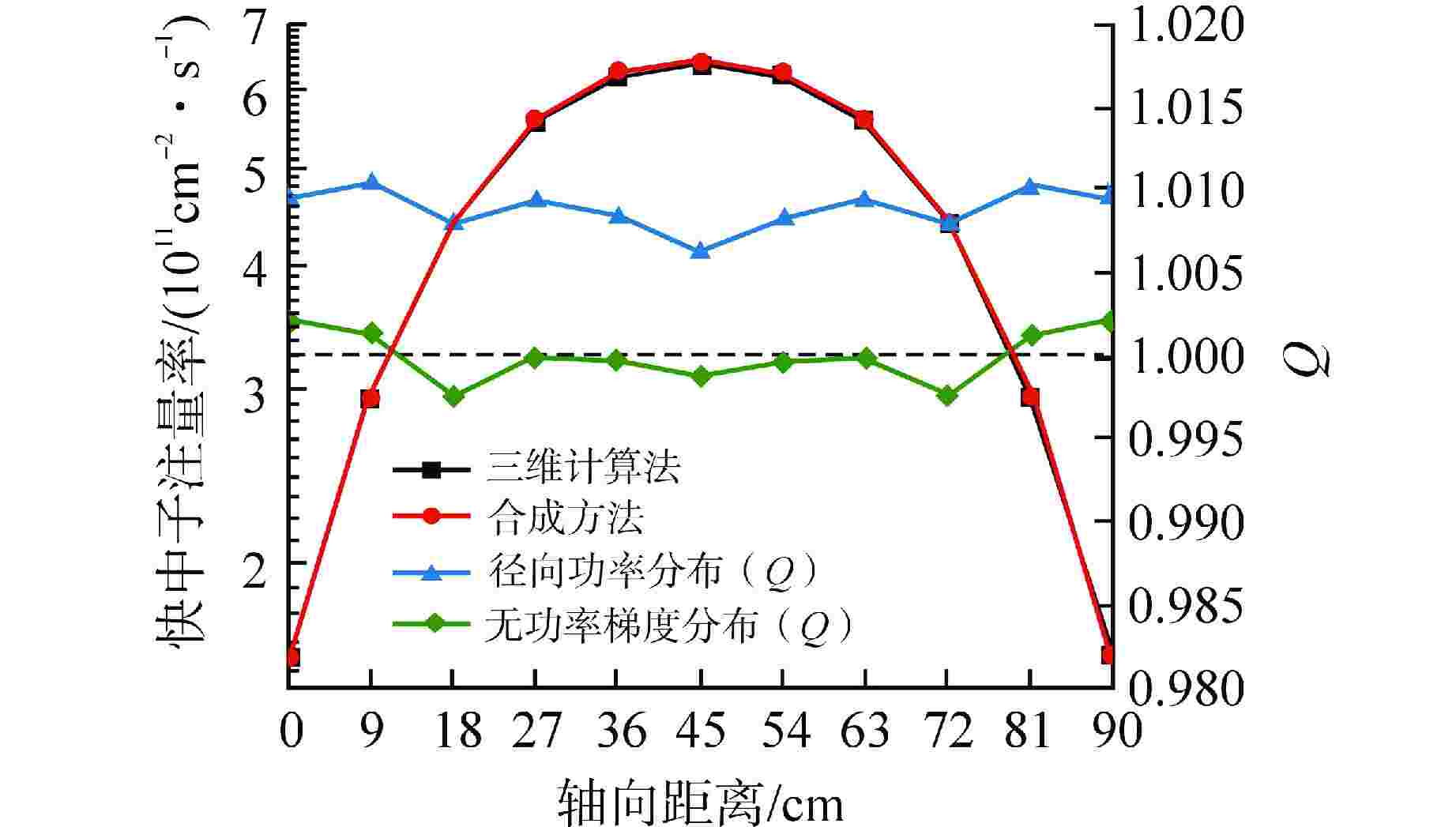
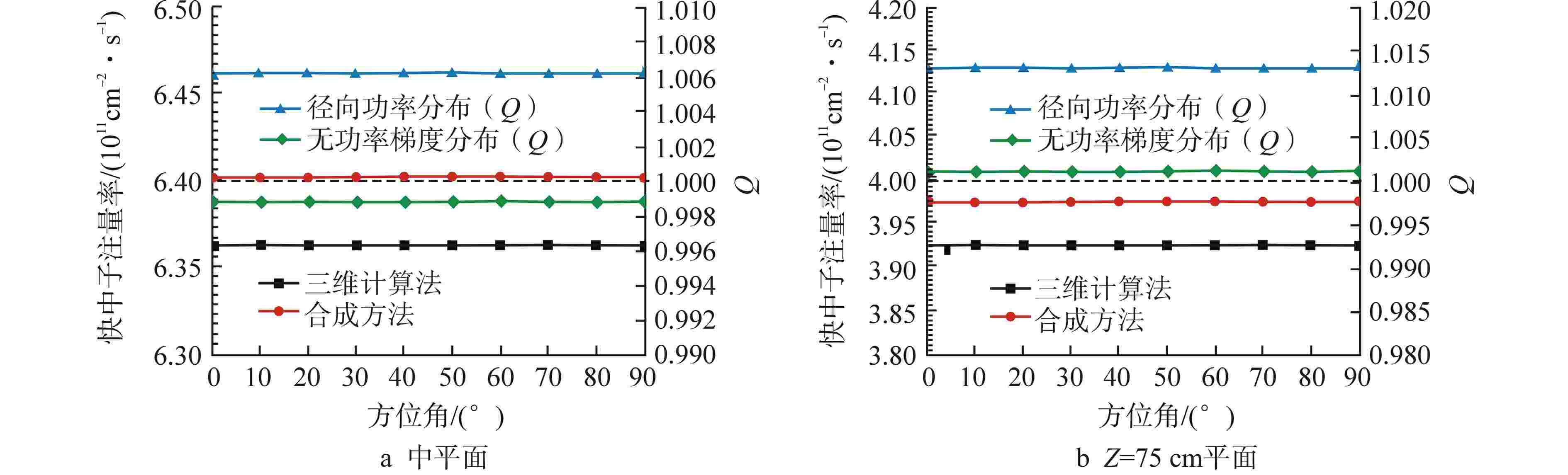
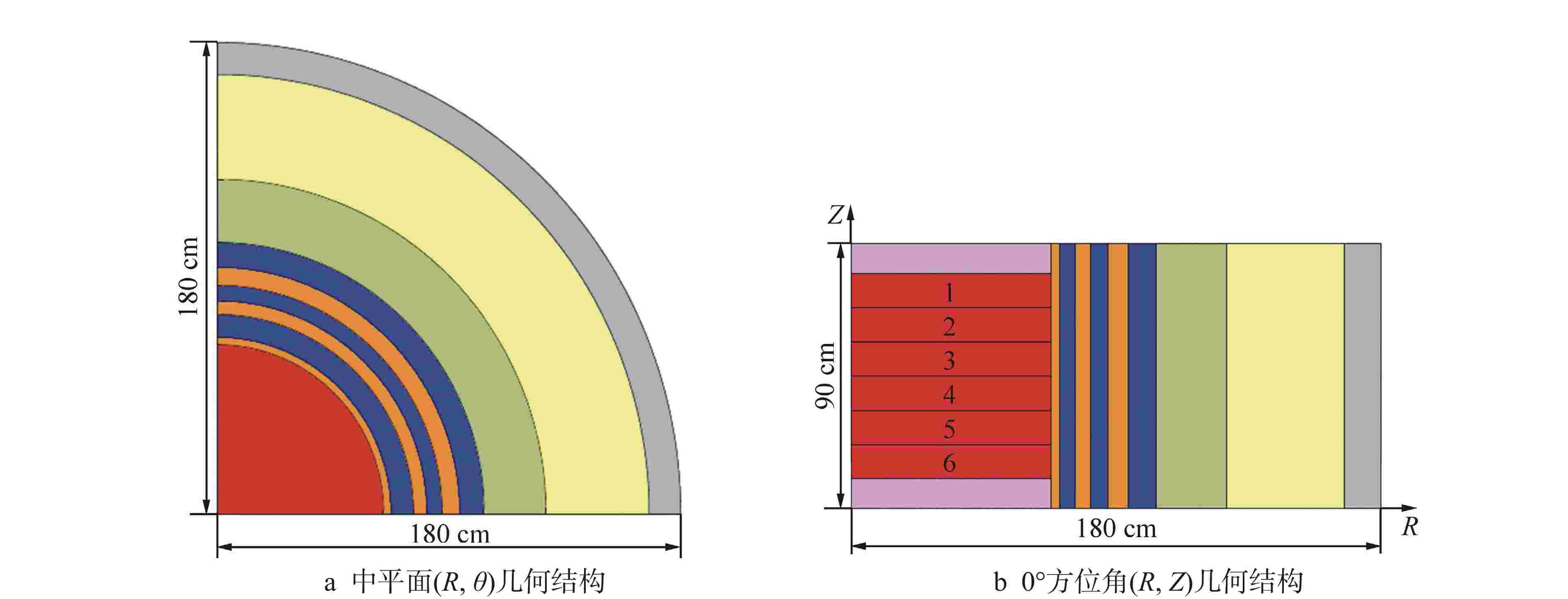
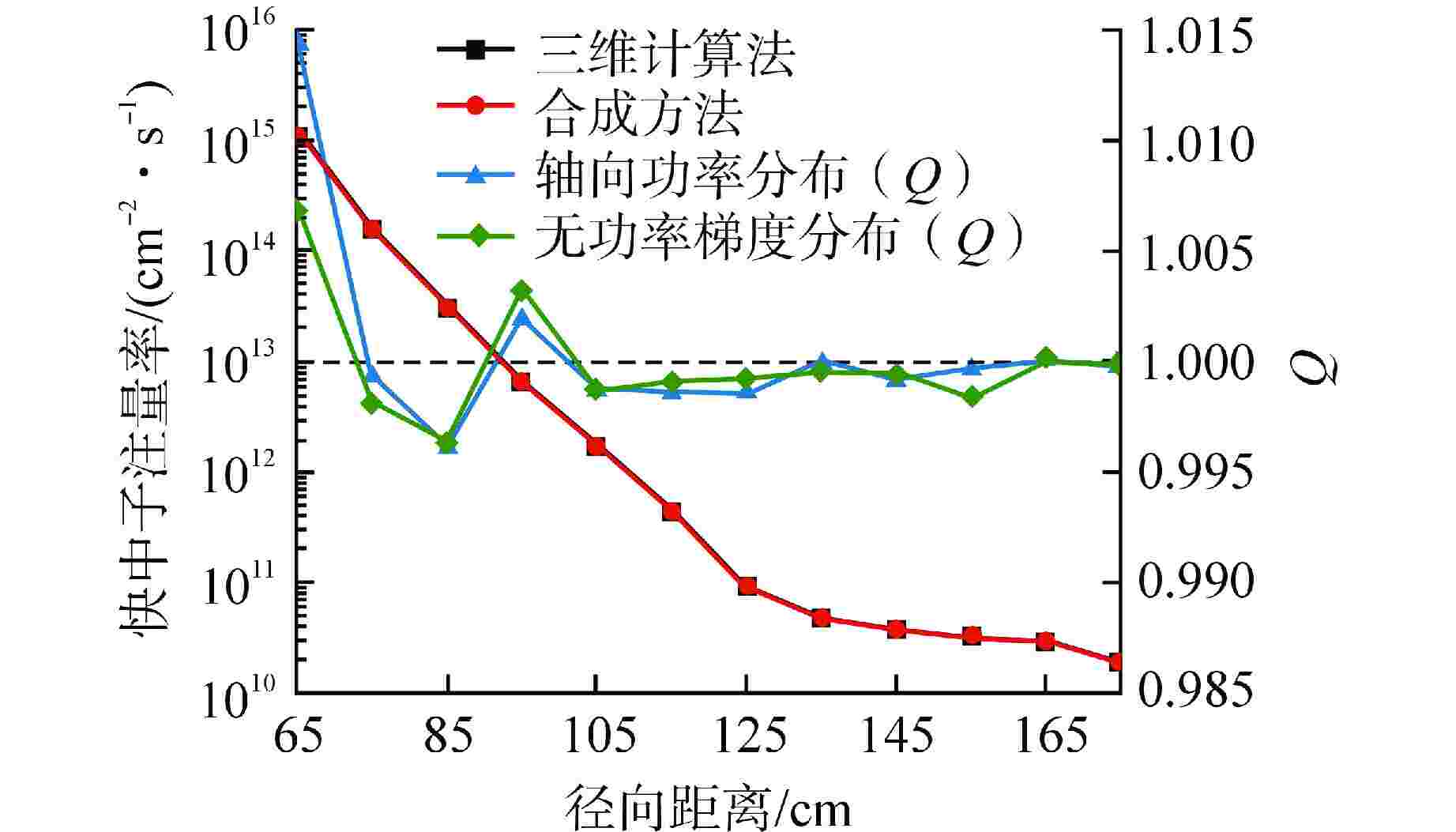
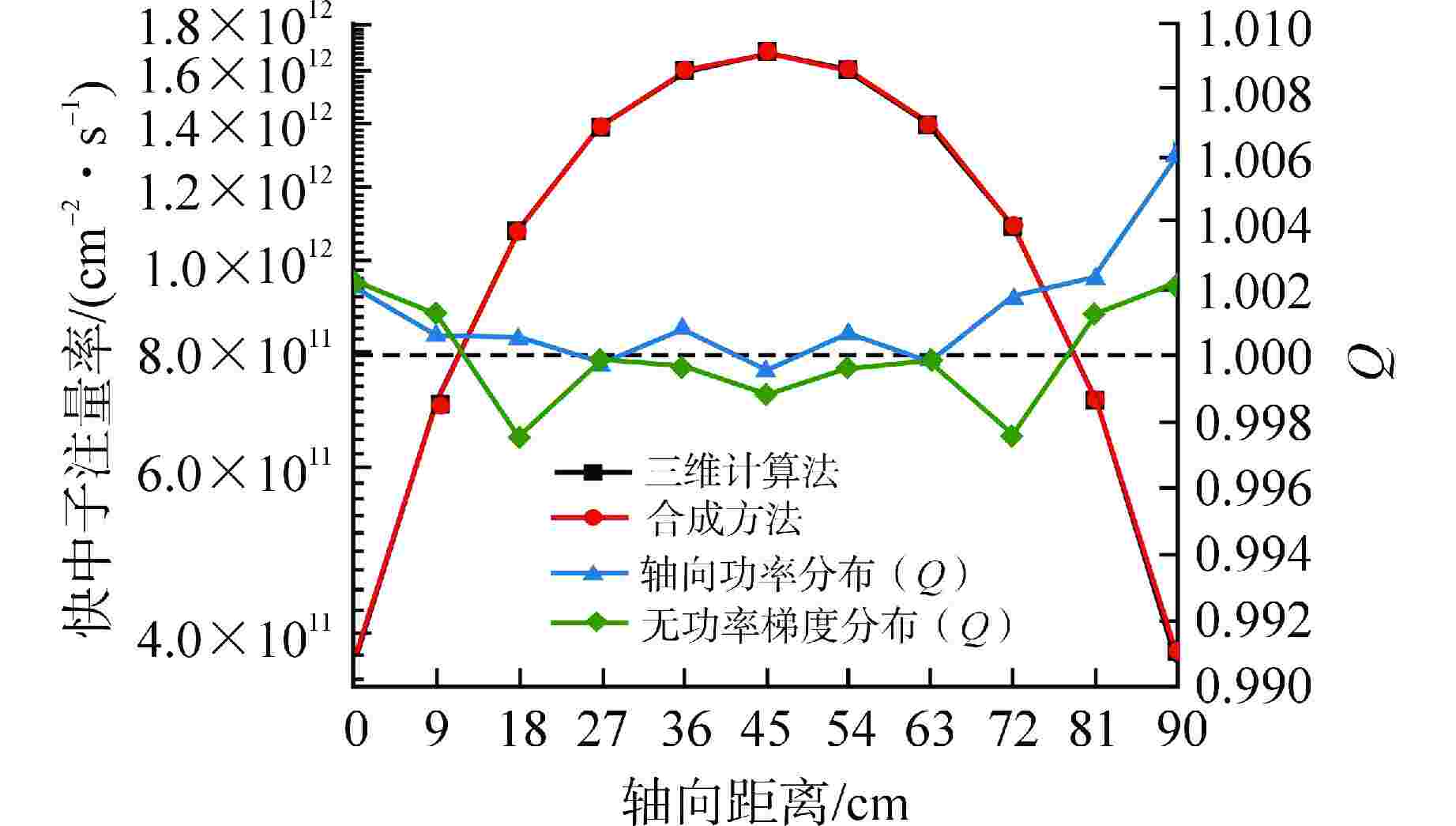
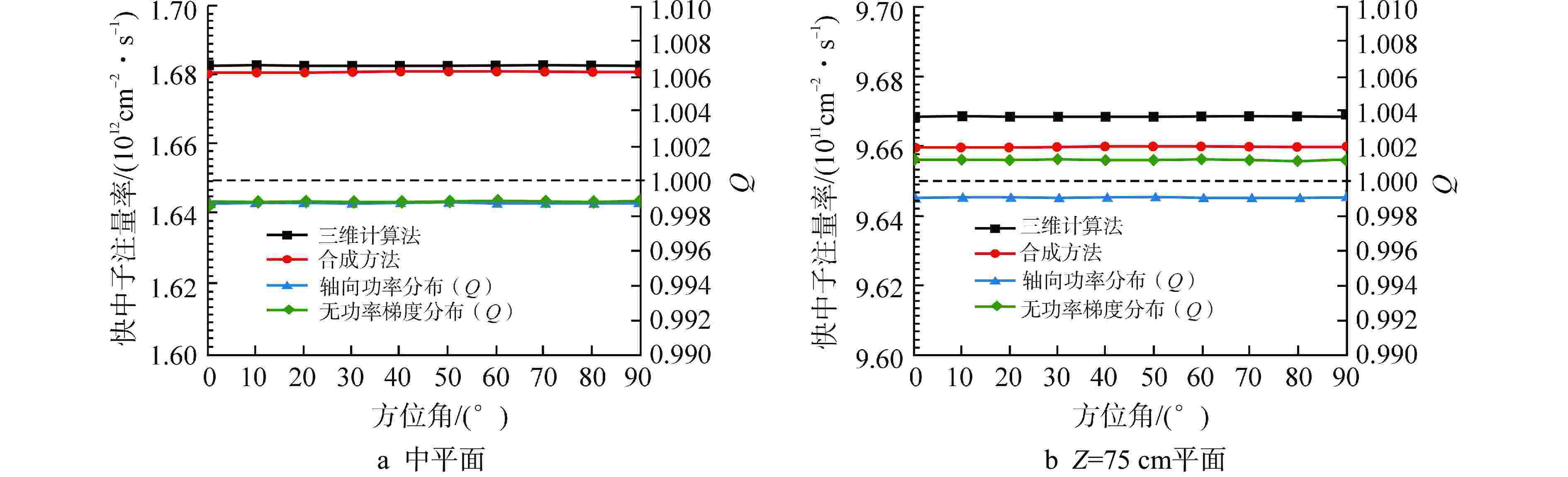
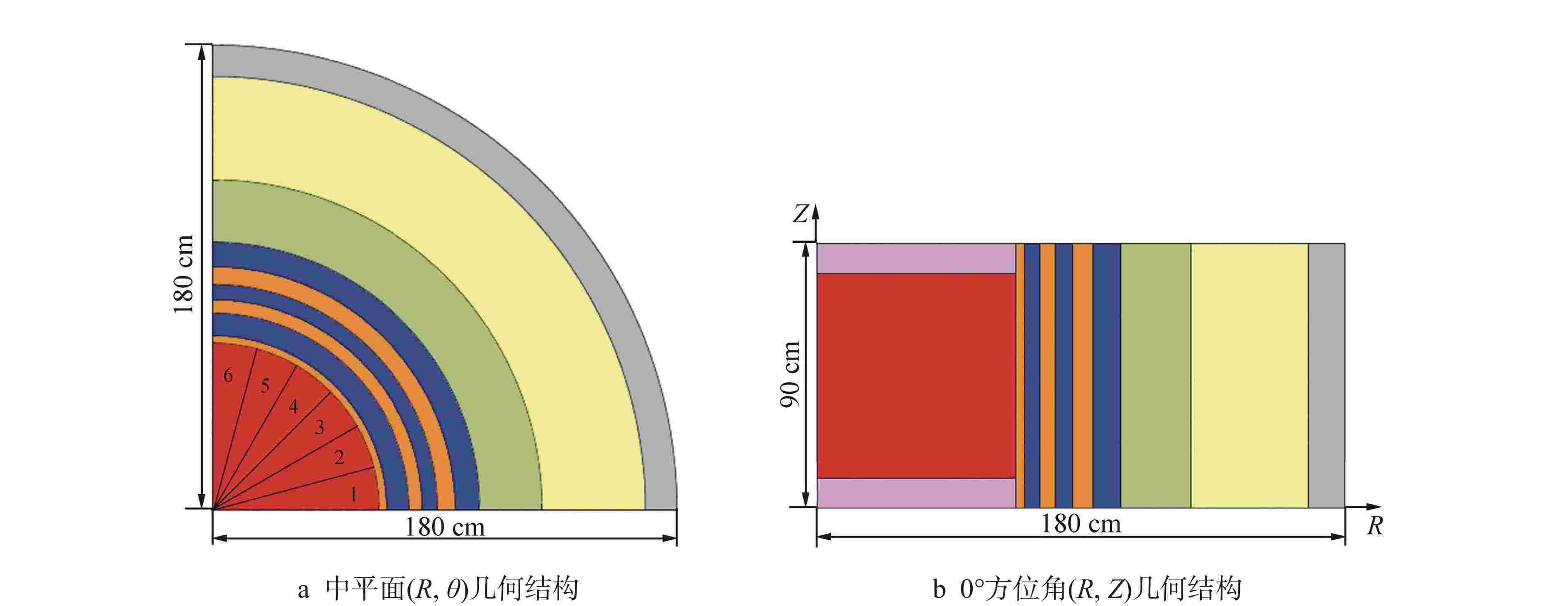
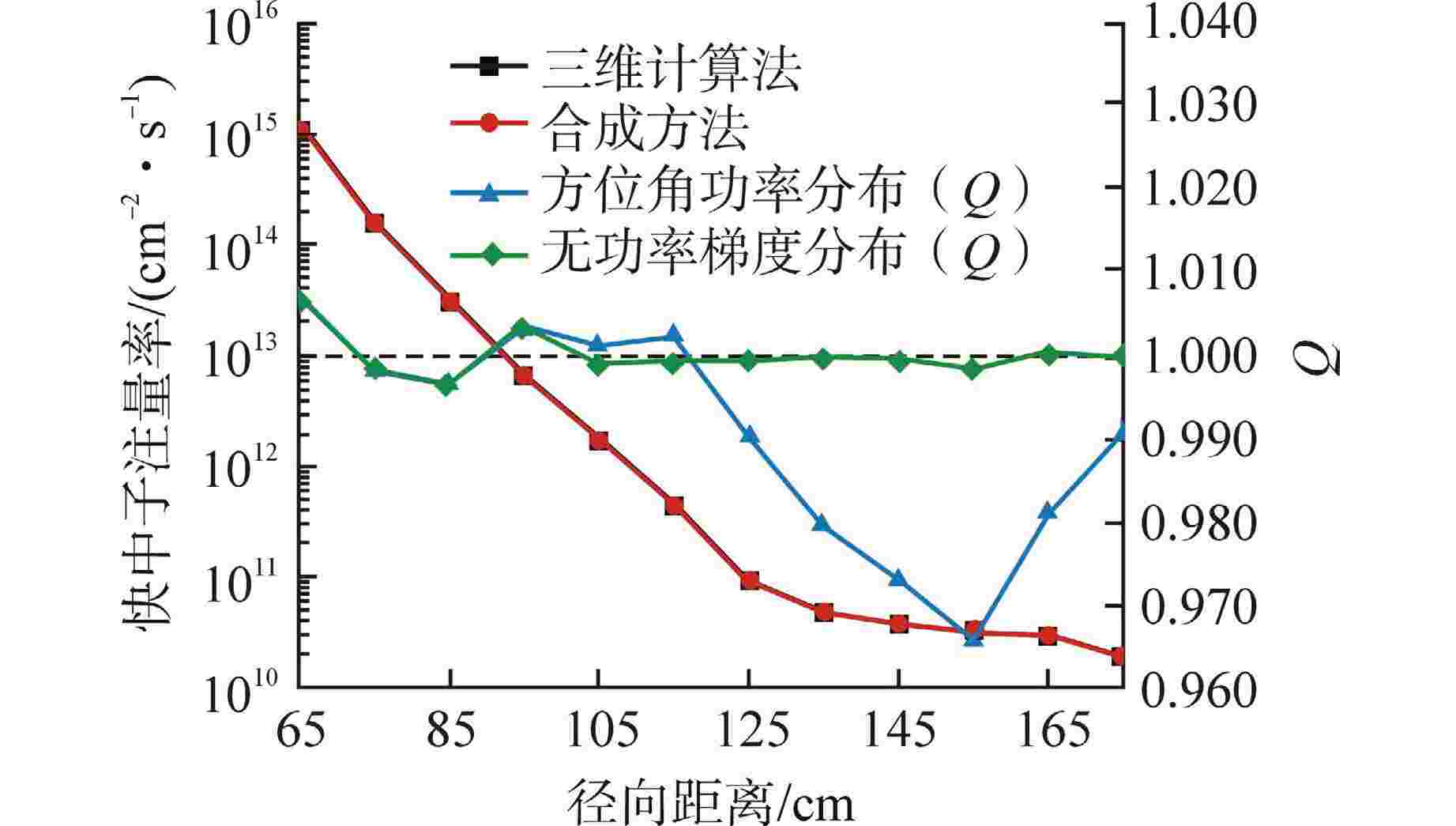
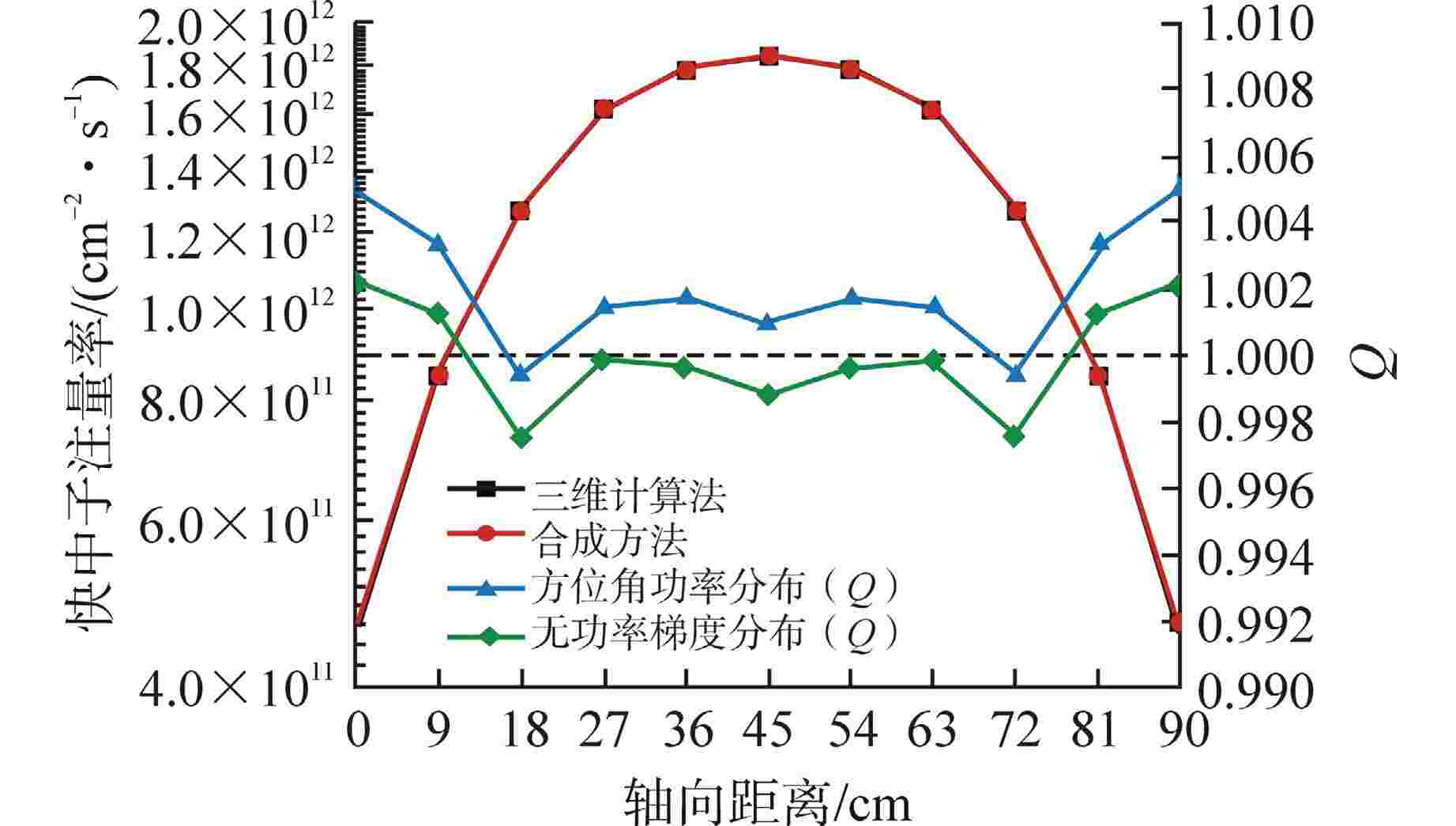
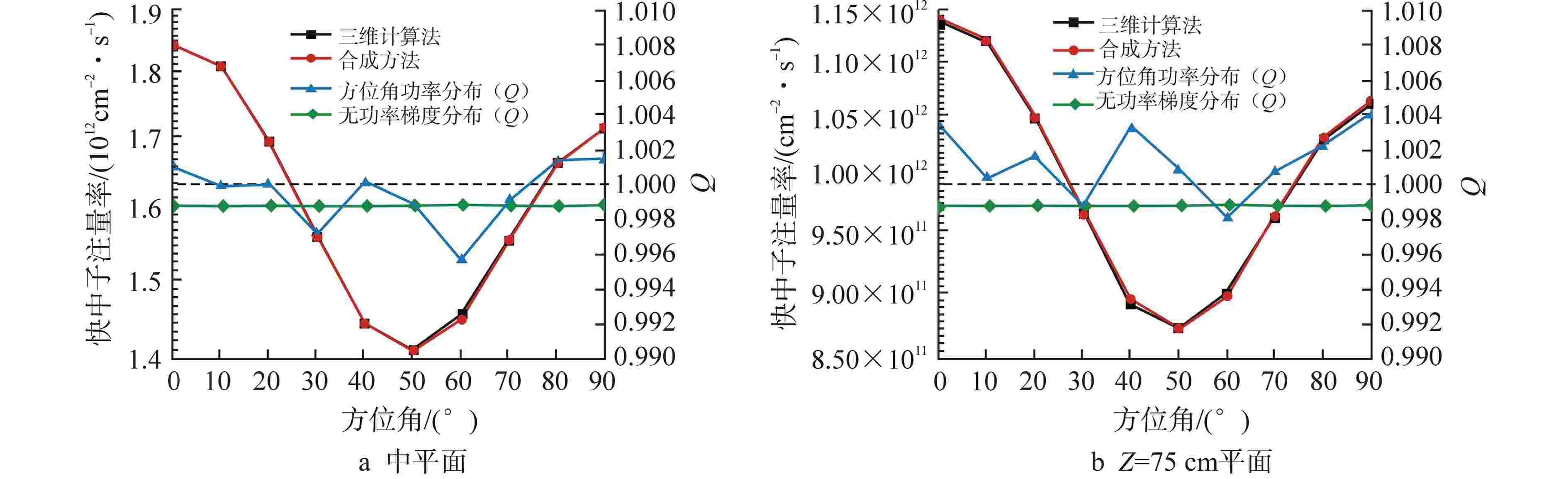
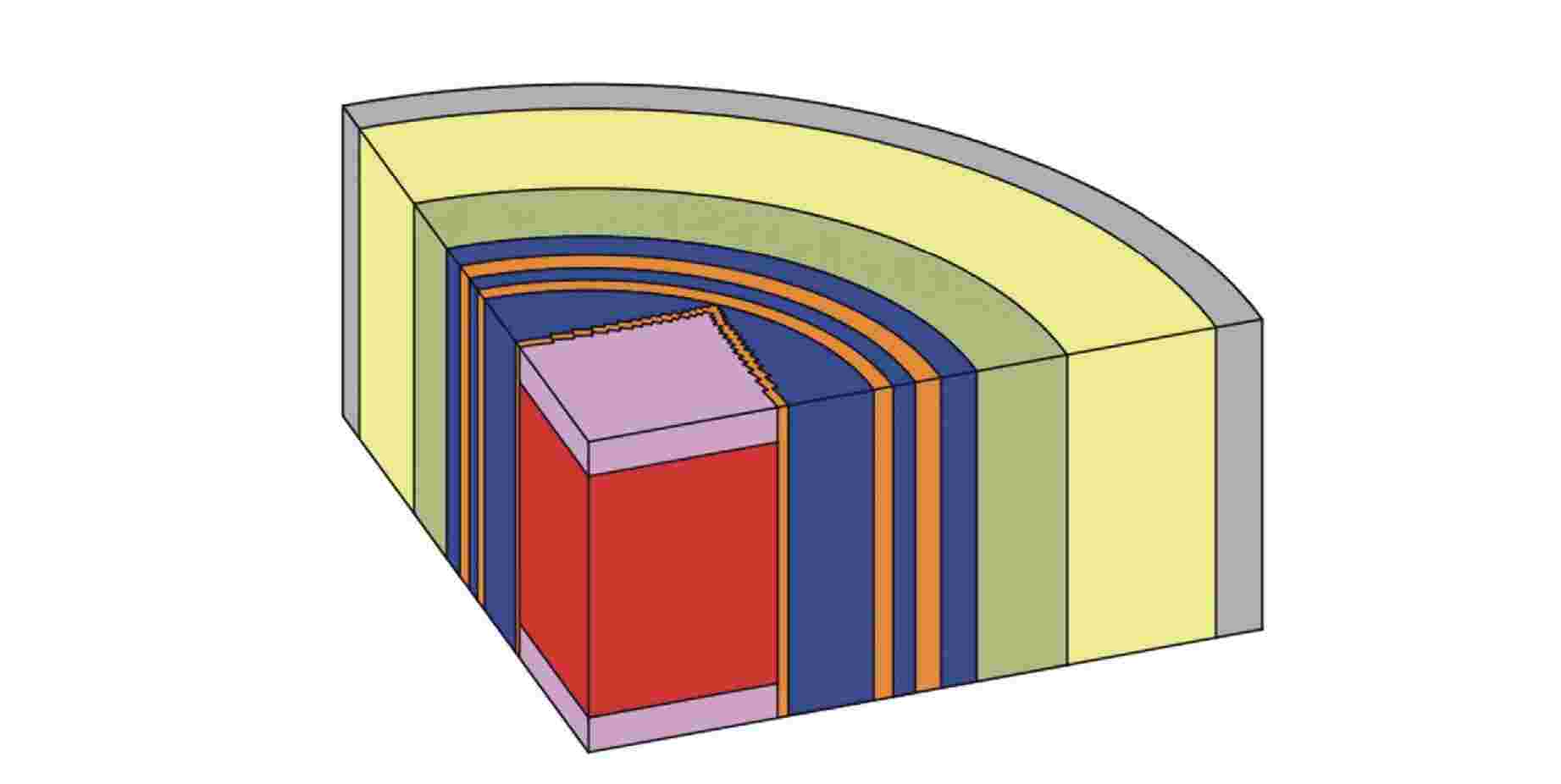
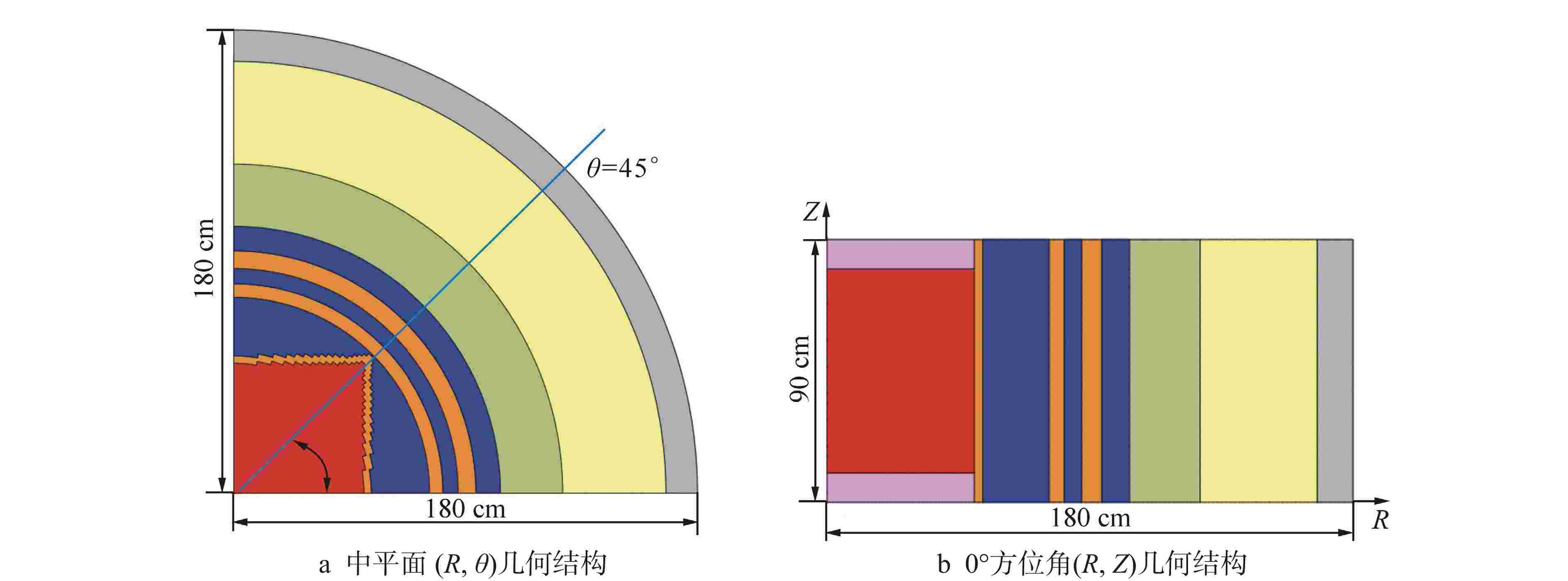
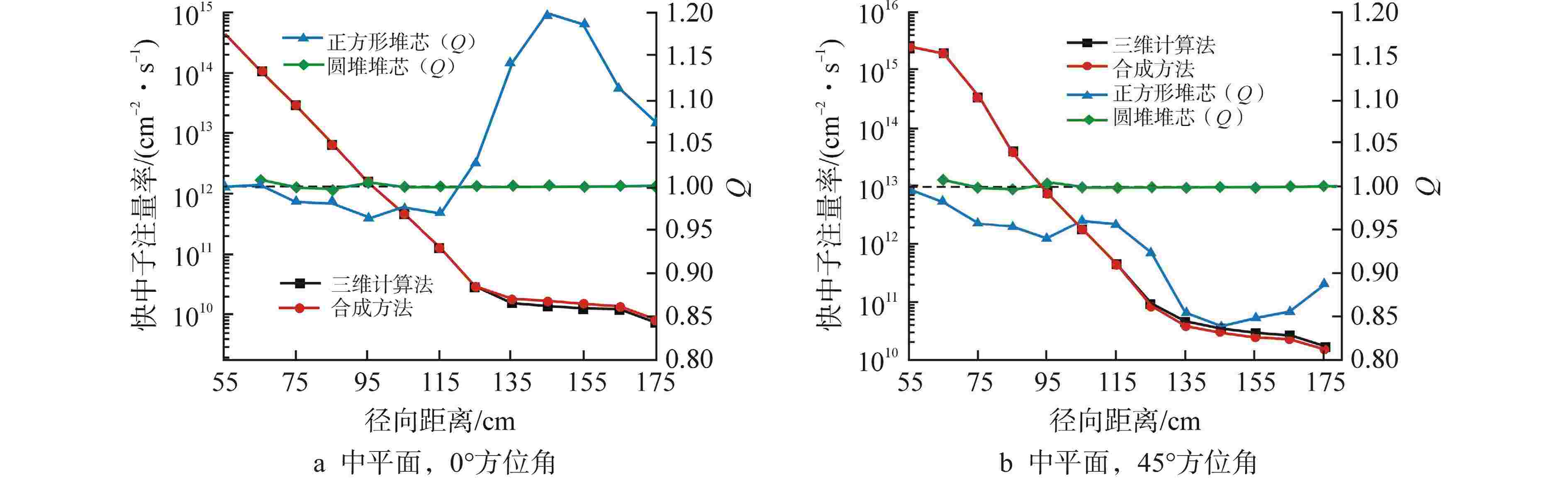
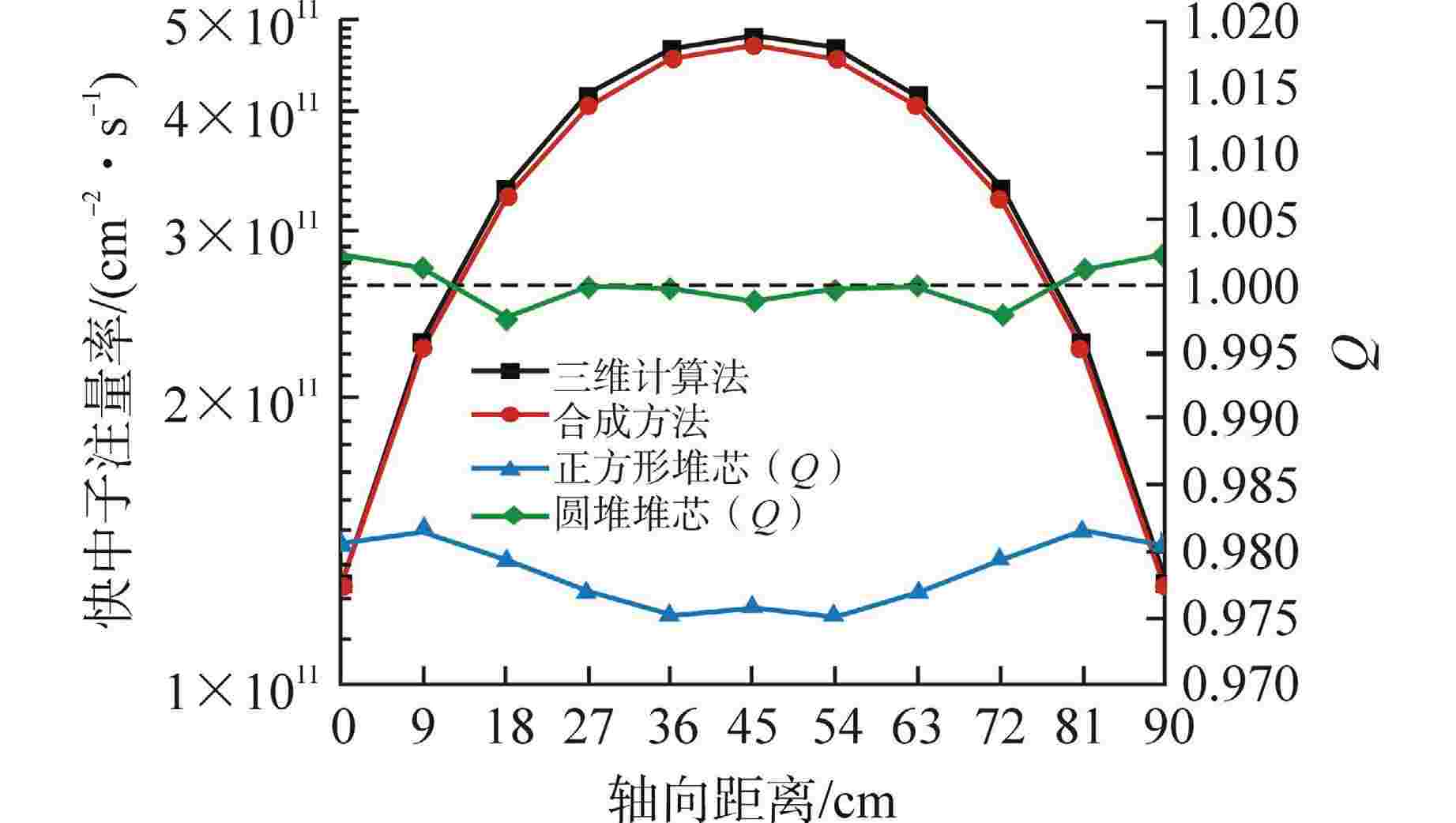
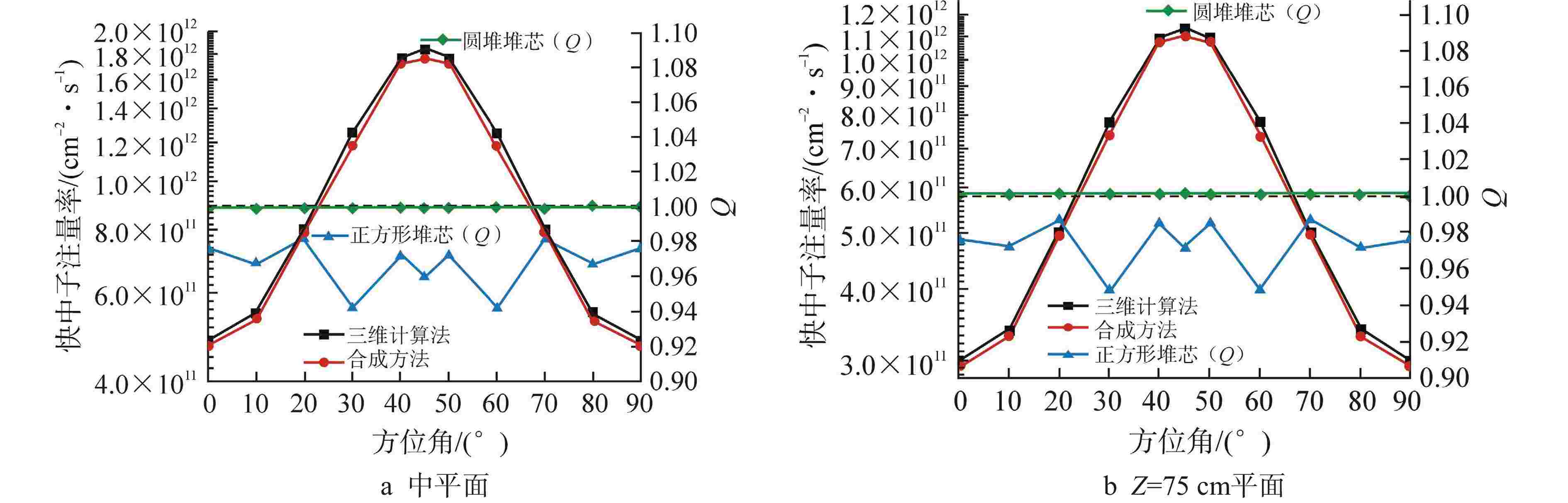
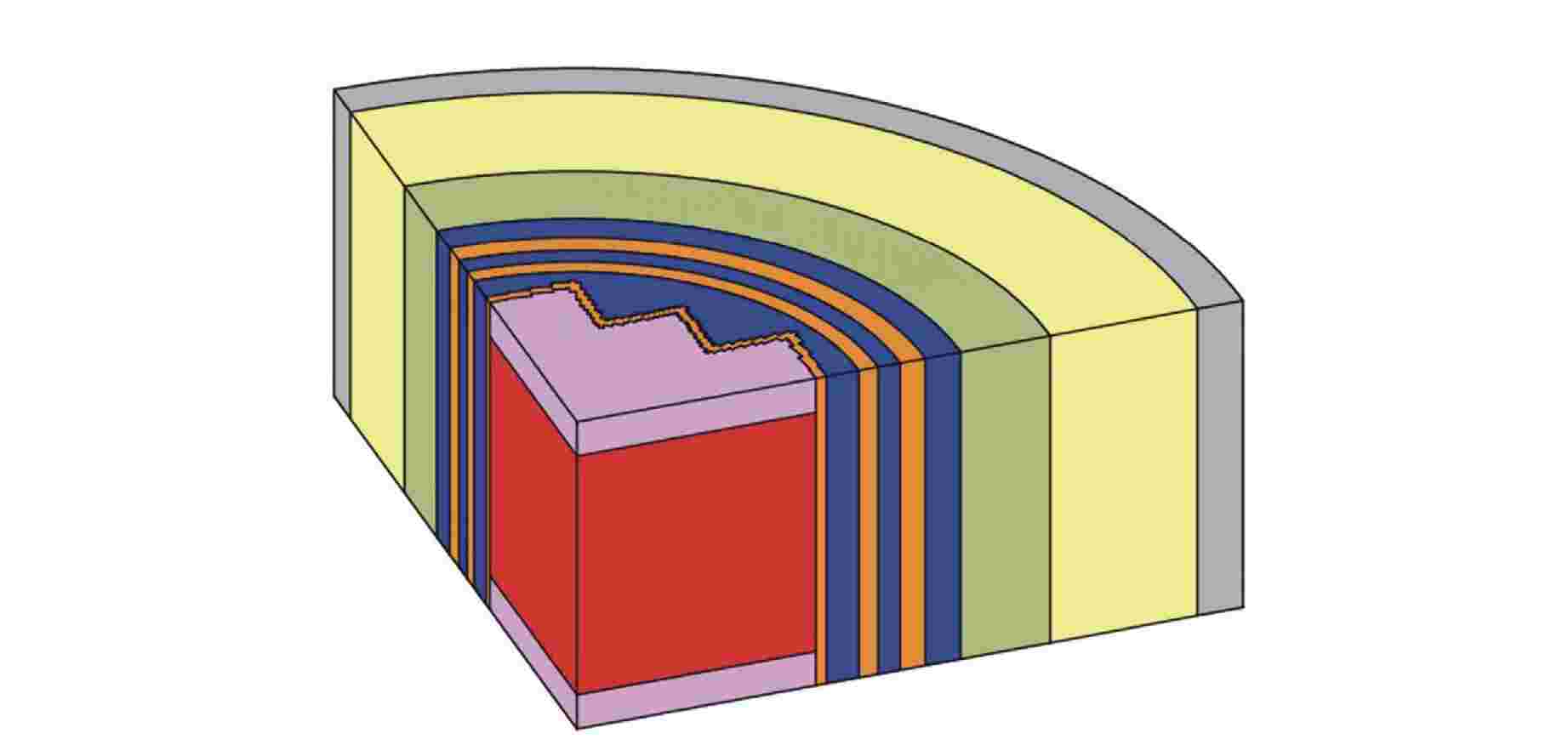
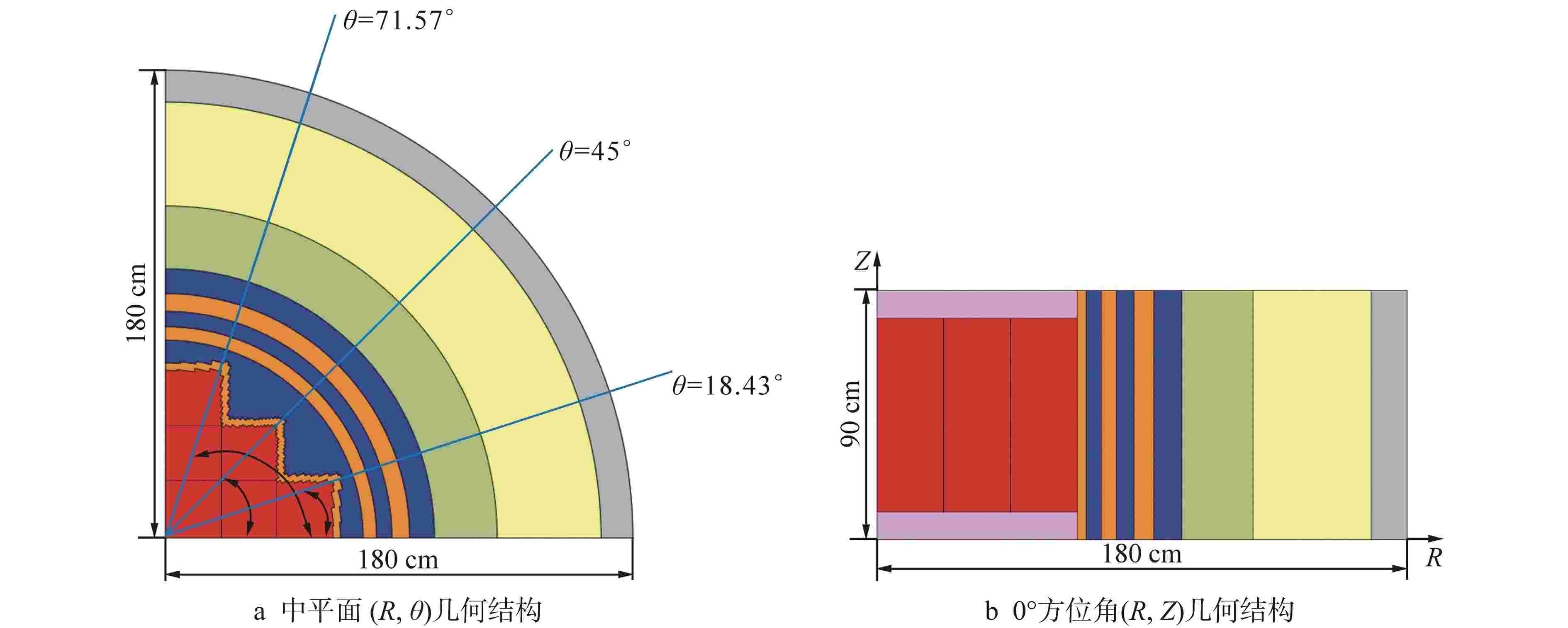
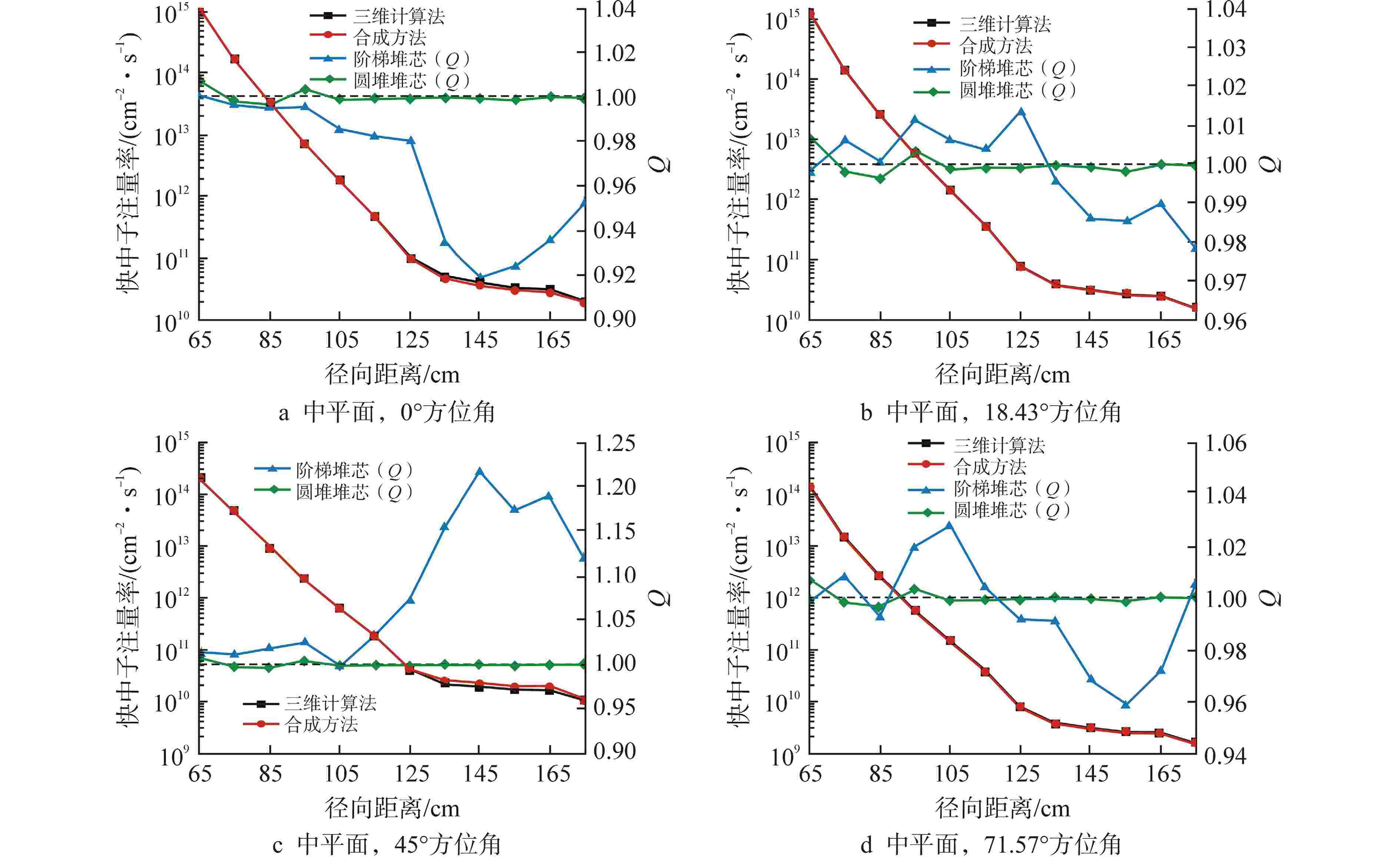
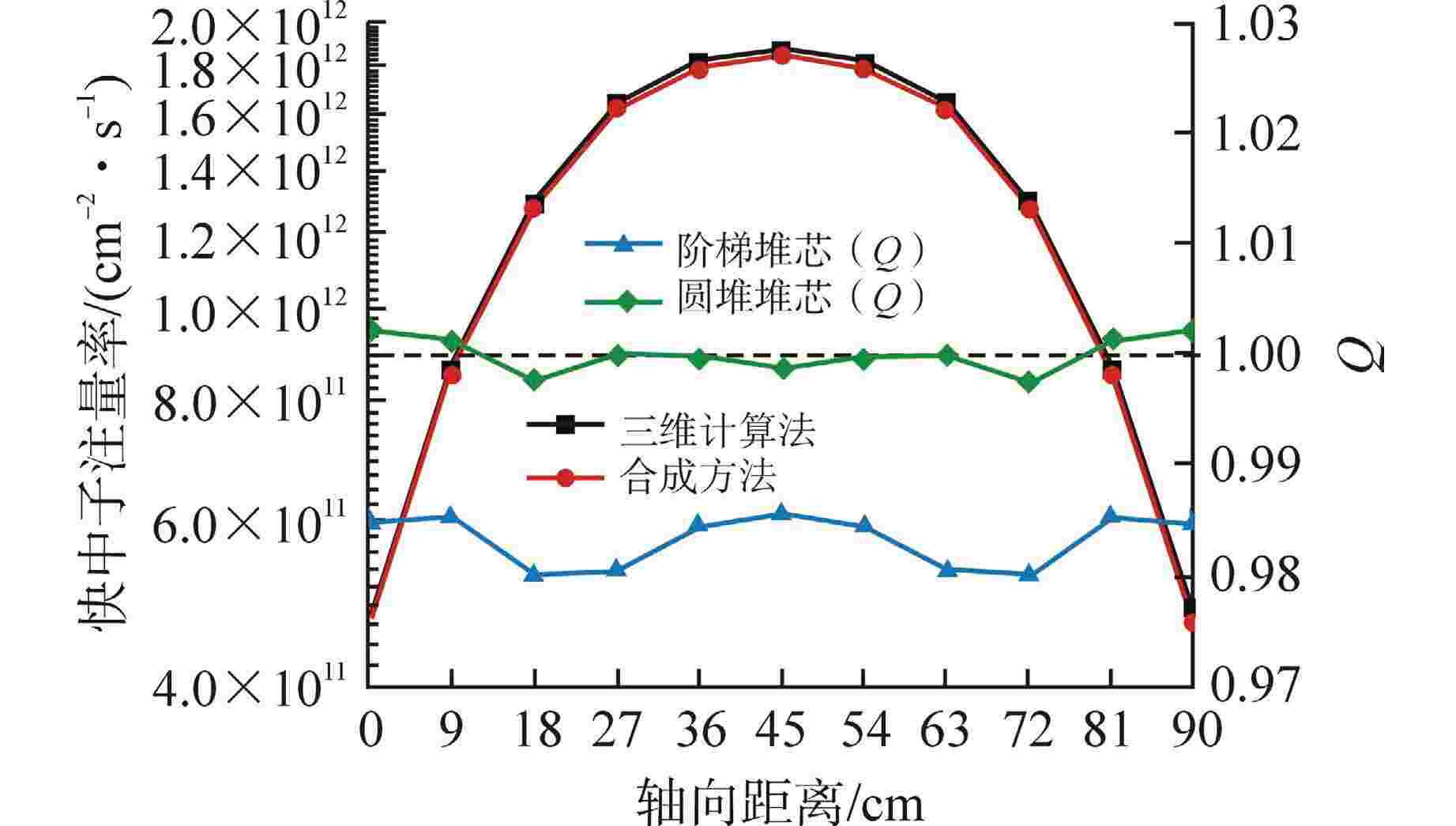
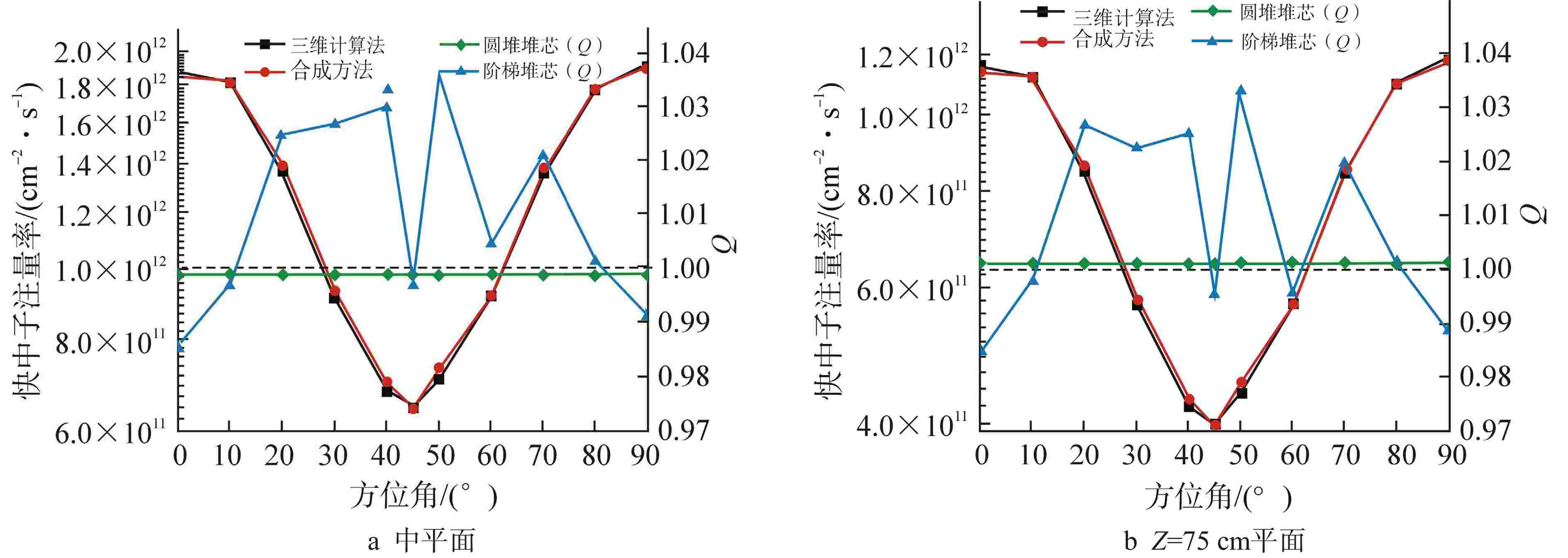
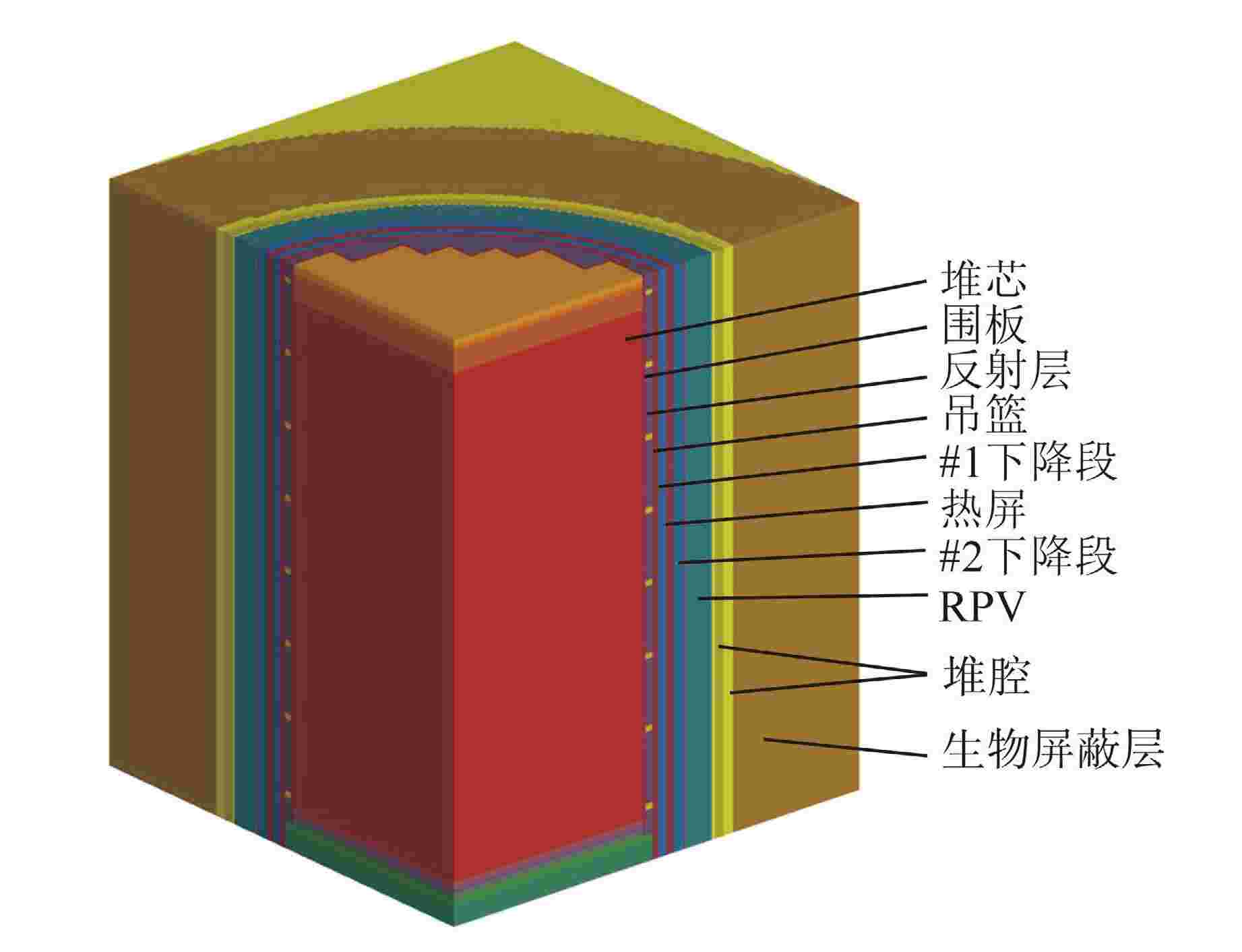
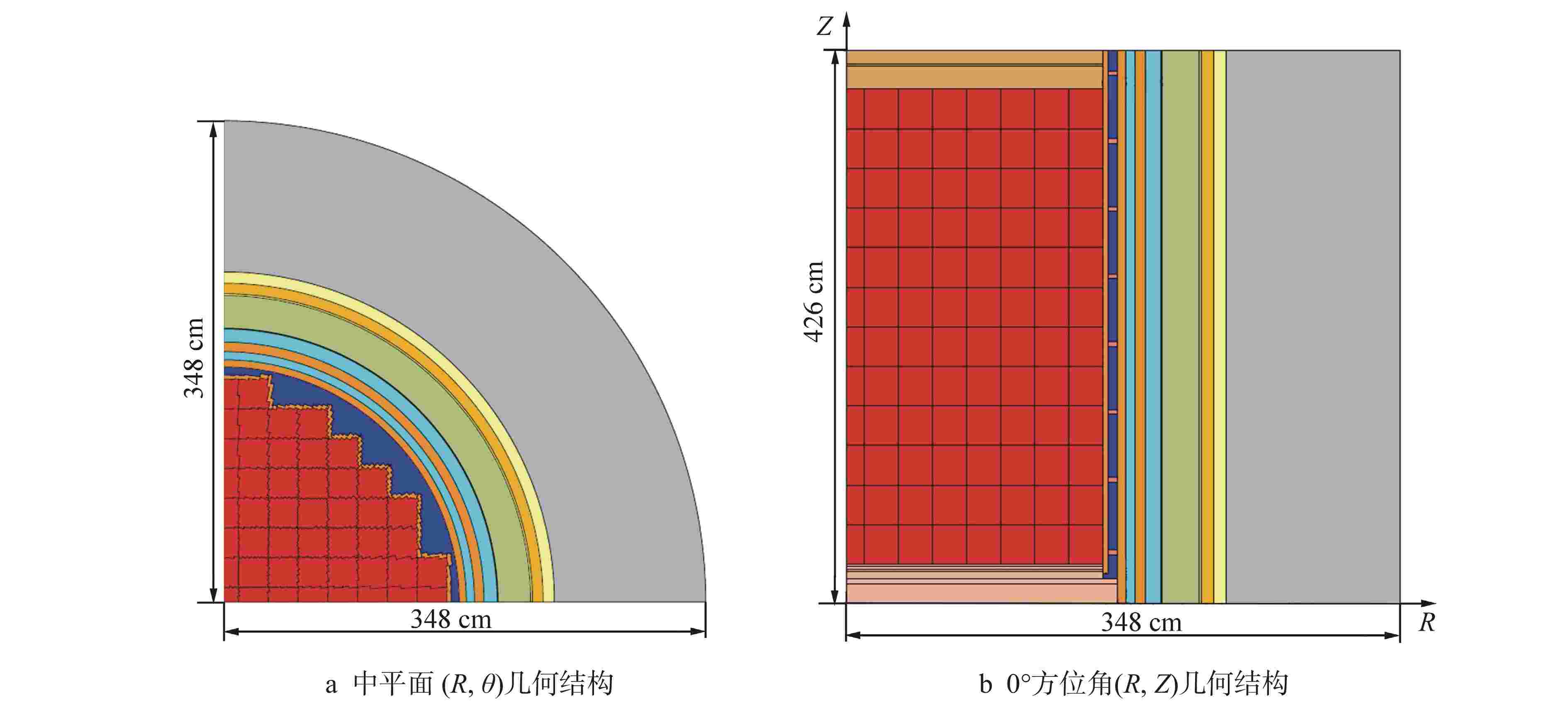
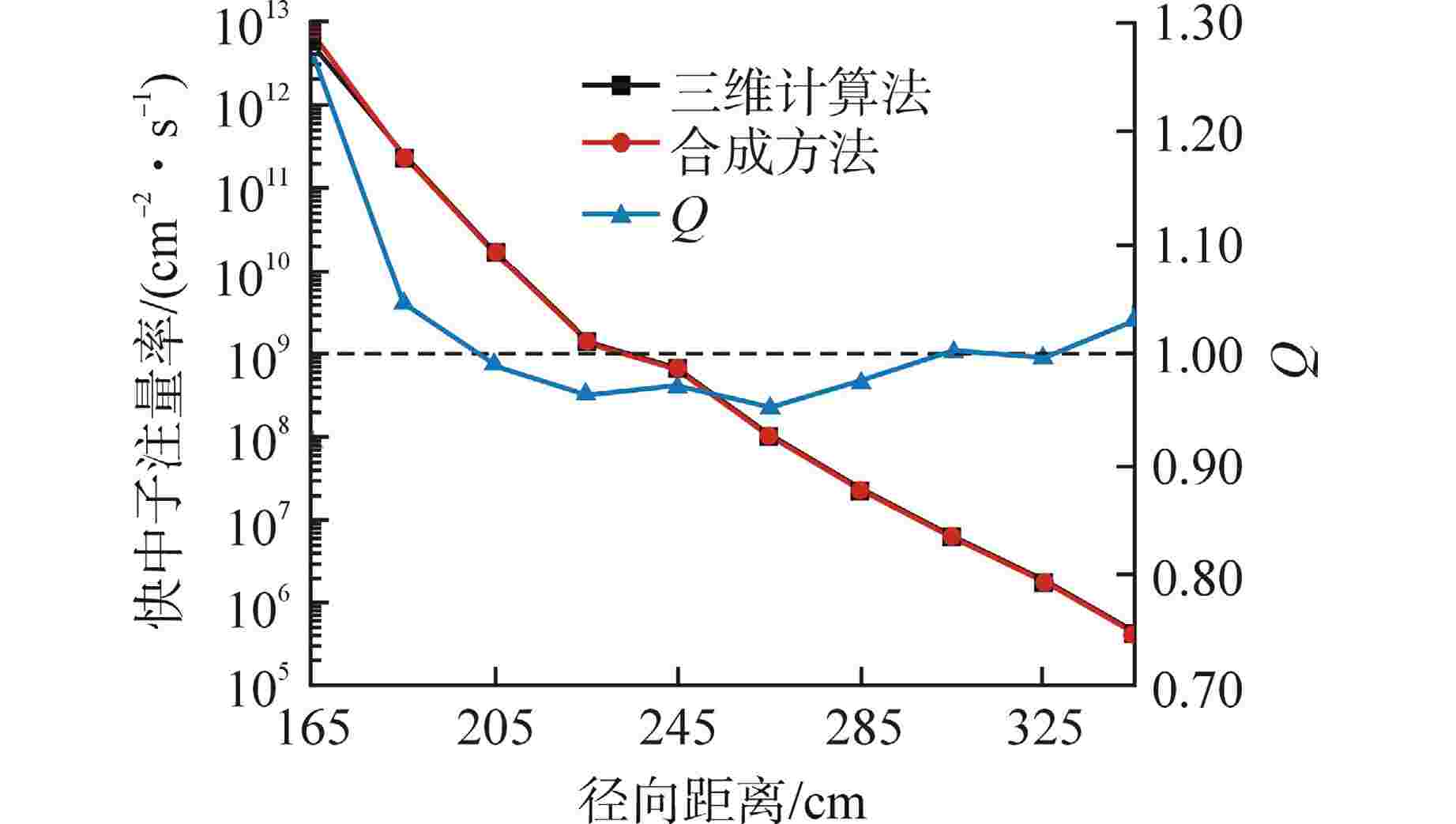
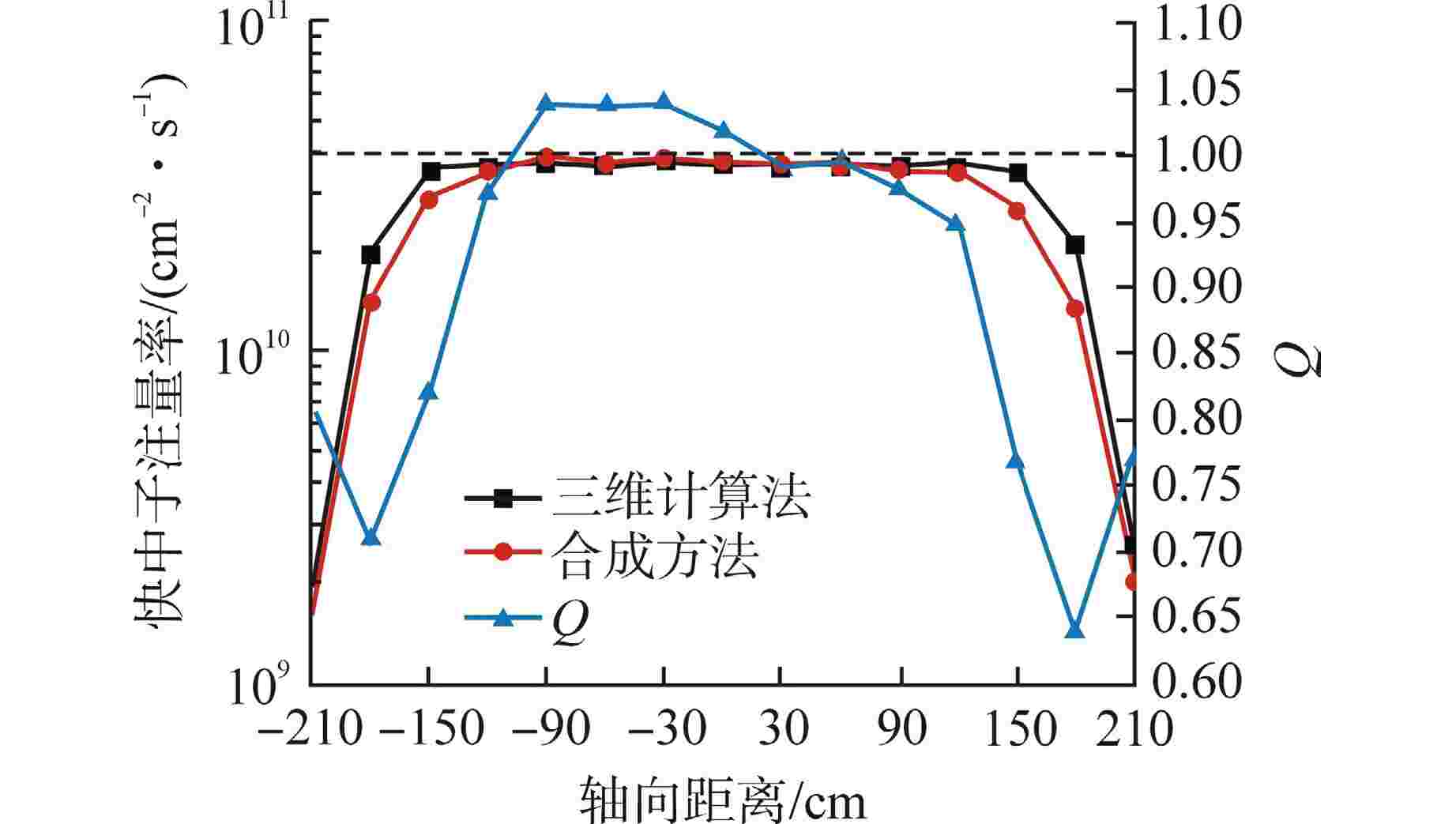
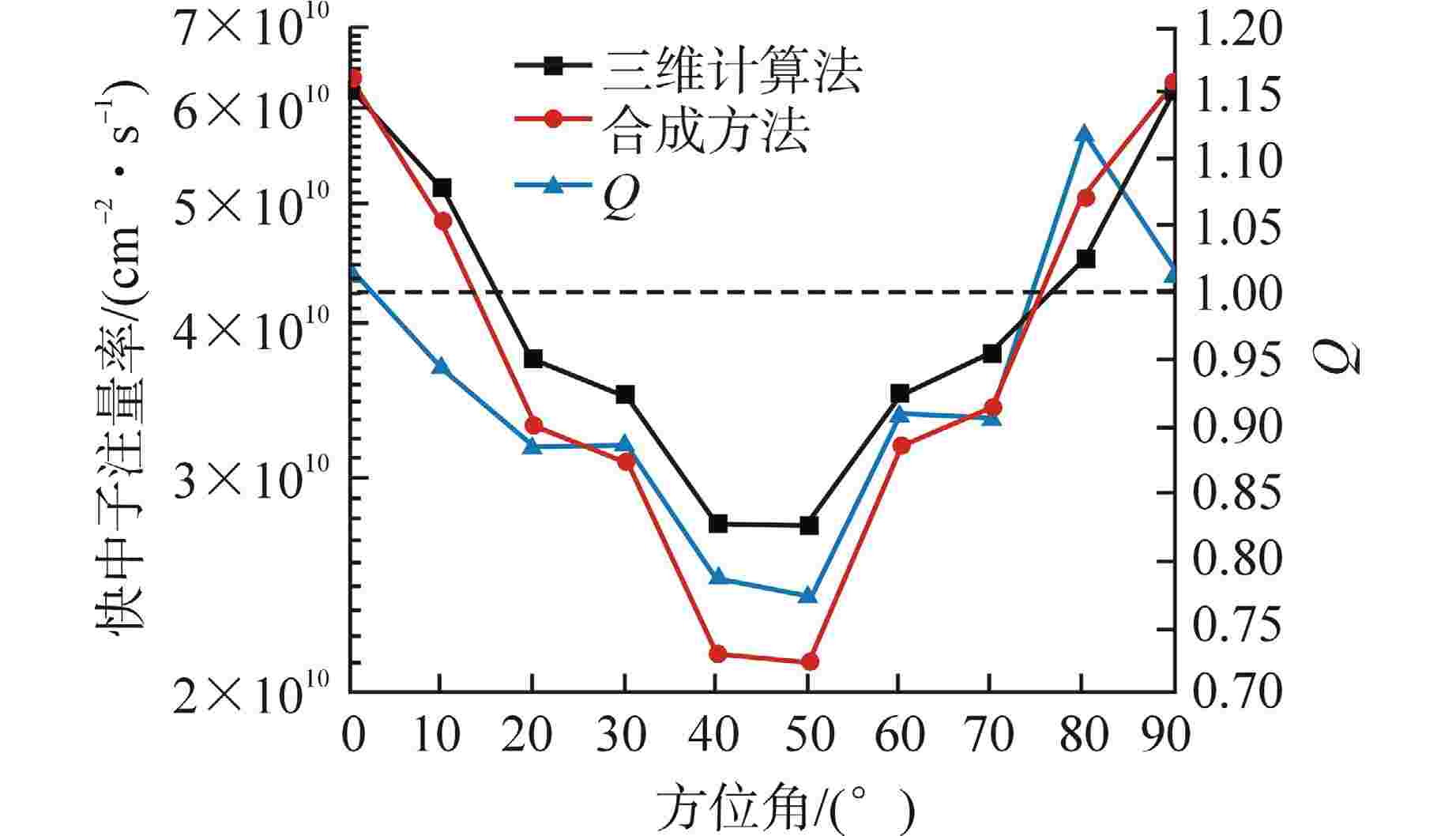
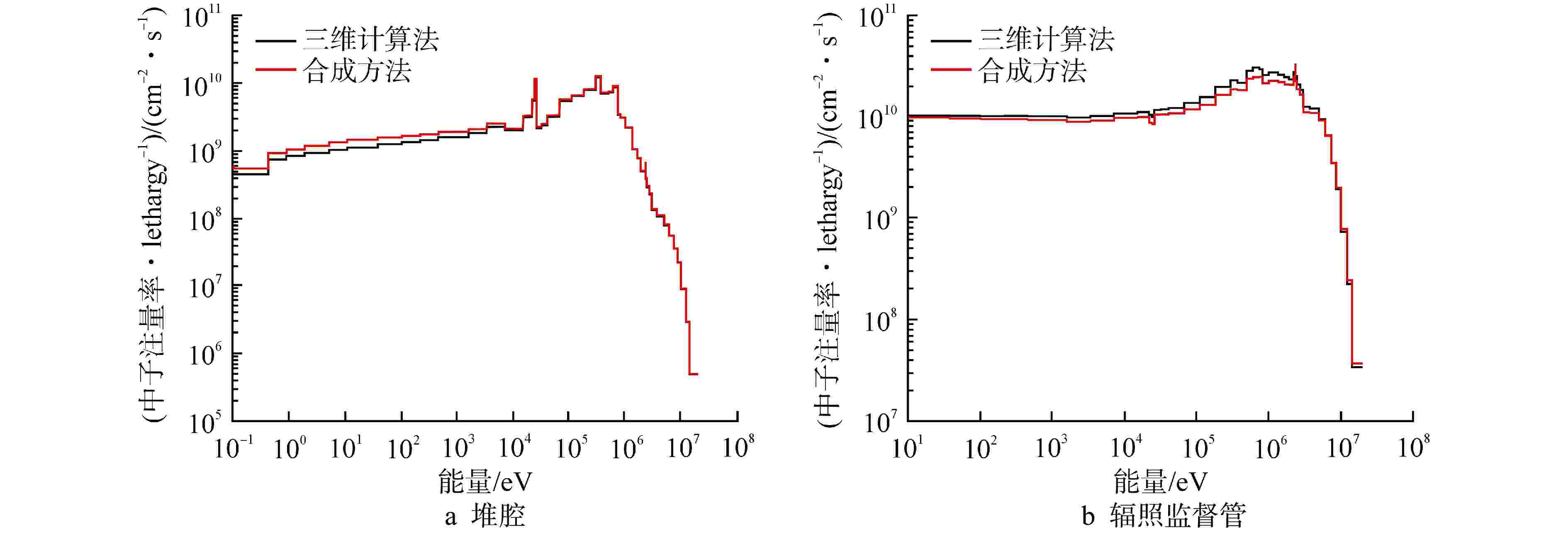
摘要: 离散纵标（SN）方法是计算反应堆压力容器（RPV）内快中子注量率的主要方法之一。基于二维加一维SN的三维注量率合成方法（简称合成方法），相比直接三维离散纵标方法（简称三维计算法）具有更高的计算效率，但源强和几何的近似处理会影响合成方法的计算精度。为深入分析源强和几何近似处理对合成方法的影响，本文建立了适用于合成方法的基准模型，并以基准模型合成与三维计算所得快中子注量率的相对误差为参考，分别分析源强和几何因素对合成方法的影响。源强分析中，在基准模型的基础上分别引入非均匀的径向、轴向和方位角功率分布，分析合成计算与三维计算所得快中子注量率相对误差的变化；在几何分析中，将基准模型的堆芯结构分别改变为正方形堆芯和阶梯状堆芯，依次分析合成计算与三维计算所得快中子注量率相对误差的变化。结果表明，径向和轴向功率分布的最大相对误差均在1.5% 以内，而方位角功率分布使堆腔处的相对误差达到3.5%；正方形和阶梯状堆芯结构分别导致堆腔处相对误差达20%和22%。在典型压水堆HBR-2计算中，合成方法与三维计算法的快中子注量率在反应堆堆腔处的相对误差达11.65%，这表明合成方法对反应堆堆腔区域的计算精度仍需要进一步提高。
-
关键词:
- 反应堆压力容器（RPV） /
- 离散纵标（SN）方法 /
- 三维注量率合成方法 /
- 快中子注量率
Abstract: The discrete ordinates (SN) method is one of the primary methods for calculating fast neutron flux in reactor pressure vessels (RPVs). The three-dimensional neutron flux synthesis method based on two-dimensional plus one-dimensional SN calculations (referred to as the synthesis method) has higher computational efficiency compared with the direct three-dimensional discrete ordinates method (referred to as the three-dimensional calculation method). However, the approximations in the source and geometry processing can affect the accuracy of the synthesis method. In order to analyze the impact of source and geometric approximations on the synthesis method, a benchmark model suitable for the synthesis method was established. The relative error of fast neutron flux calculated by the synthesis method and the three-dimensional calculation of the benchmark model is used as a reference to analyze the influence of source and geometric factors on the synthesis method. In the analysis of source effects, non-uniform radial, axial, and azimuthal power distributions are introduced into the benchmark model to examine the changes in the relative error of fast neutron flux between synthetic calculations and three-dimensional calculations. In the analysis of geometric effects, the core structure of the benchmark model is altered to a square core and a stepped core, respectively, to sequentially analyze the changes in the relative error of fast neutron flux between synthetic and three-dimensional calculations. The results indicate that the maximum relative errors caused by the radial and axial power distributions are both within 1.5%, while the azimuthal power distribution leads to a relative error of 3.5% at the reactor cavity. The square and stepped core structures result in relative errors of 20% and 22%, respectively, in the cavity. In the computations for the typical pressurized water reactor HBR-2, the relative error between the synthesis method and the three-dimensional fast neutron flux calculations at the cavity was 11.65%. These findings demonstrate that the accuracy of the synthesis method for the reactor cavity region still requires improvement. -
图 4 基准模型快中子注量率径向分布（中平面，0°方位角）
Figure 4. Radial Profile of Fast Neutron Flux in the Benchmark Model (Midplane, 0° Azimuth)
图 5 基准模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 5. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Benchmark Model (0° Azimuth)
图 6 基准模型RPV内壁快中子注量率圆周方向分布
Figure 6. Circumferential Profile of Fast Neutron Flux on the RPV Inner Wall in the Benchmark Model
图 8 径向功率分布模型快中子注量率径向分布（中平面，0°方位角）
Figure 8. Radial Profile of Fast Neutron Flux in the Radial Power Distribution Model (Midplane, 0° Azimuth)
图 9 径向功率分布模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 9. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Radial Power Distribution Model (0° Azimuth)
图 10 径向功率分布模型RPV内壁快中子注量率圆周方向分布
Figure 10. Circumferential Profile of Fast Neutron Flux on the RPV Inner Wall in the Radial Power Distribution Model
图 12 轴向功率分布模型快中子注量率径向分布（中平面，0°方位角）
Figure 12. Radial Profile of Fast Neutron Flux in the Axial Power Distribution Model (Midplane, 0° Azimuth)
图 13 轴向功率分布模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 13. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Axial Power Distribution Model (0° Azimuth)
图 14 轴向功率分布模型RPV内壁快中子注量率方位角分布
Figure 14. Azimuthal Profile of Fast Neutron Flux on the RPV Inner Wall in the Axial Power Distribution Model
图 16 方位角功率分布模型的快中子注量率径向分布（中平面，0°方位角）
Figure 16. Radial Profile of Fast Neutron Flux in the Azimuthal Power Distribution Model (Midplane, 0° Azimuth)
图 17 方位角功率分布模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 17. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Azimuthal Power Distribution Model (0° Azimuth)
图 18 方位角功率分布模型RPV内壁快中子注量率圆周方向分布
Figure 18. Circumferential Profile of Fast Neutron Flux on the RPV Inner Wall in the Azimuthal Power Distribution Model
图 21 正方形堆芯模型快中子注量率径向分布
Figure 21. Radial Profile of Fast Neutron Flux in the Square Core Model
图 22 正方形堆芯模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 22. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Square Core Model (0° Azimuth)
图 23 正方形堆芯模型RPV内壁快中子注量率圆周方向分布
Figure 23. Circumferential Profile of Fast Neutron Flux on the RPV Inner Wall in the Square Core Model
图 26 阶梯状堆芯模型快中子注量率径向分布
Figure 26. Radial Profile of Fast Neutron Flux in the Stepped Core Model
图 27 阶梯状堆芯模型RPV内壁快中子注量率轴向分布（0°方位角）
Figure 27. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in the Stepped Core Model (0° Azimuth)
图 28 阶梯状堆芯模型RPV内壁快中子注量率圆周方向分布
Figure 28. Circumferential Profile of Fast Neutron Flux on the RPV Inner Wall in the Stepped Core Model
图 31 HBR-2快中子注量率径向分布（中平面，0°方位角）
Figure 31. Radial Profile of Fast Neutron Flux in HBR-2 (Midplane, 0° Azimuth)
图 32 HBR-2 RPV内壁快中子注量率轴向分布（0°方位角）
Figure 32. Axial Profile of Fast Neutron Flux on the RPV Inner Wall in HBR-2 (0° Azimuth)
图 33 HBR-2辐照监督管处快中子注量率圆周方向分布（中平面）
Figure 33. Circumferential Profile of Fast Neutron Flux at the Surveillance Capsule in HBR-2 (Midplane)
表 1 径向功率分布
Table 1. Radial Power Distribution
组件编号 1 2 3 4 5 6 7 8 组件相对功率 1.007 1.169 1.019 1.256 1.008 0.951 1.095 0.444 
下载: 导出CSV
-
[1] CAREW J F, HU K, ARONSON A, et al. PWR and BWR pressure vessel fluence calculation benchmark problems and solutions: NUREG/CR-6115[R]. Washington: Division of Engineering Technology, Office of Nuclear Regulatory Research, U. S. Nuclear Regulatory Commission, 2001. [2] U. S. Nuclear Regulatory Commission. Radiation embrittlement of reactor vessel materials: Regulatory Guide 1.99[R]. Rockville: U. S. Nuclear Regulatory Commission, 1988. [3] PETROVIC B G, HAGHIGHAT A. Effects of SN method numerics on pressure vessel neutron fluence calculations[J]. Nuclear Science and Engineering, 1996, 122(2): 167-193. doi: 10.13182/NSE96-3 [4] BOEHMER B, BORODKIN G, KONHEISER J, et al. Testing of neutron data libraries in application to reactor pressure vessel dosimetry[J]. Journal of Nuclear Science and Technology, 2002, 39(S2): 1006-1009. [5] KULESZA J A. Comparison of three-dimensional flux synthesis and full three-dimensional discrete ordinates methods for the calculation of reactor cavity bioshield heat generation rates[J]. Nuclear Technology, 2011, 175(1): 228-237. doi: 10.13182/NT11-A12294 [6] LIM M J, MAENG Y J, FERO A H, et al. Comparison of analysis results between 2D/1D synthesis and RAPTOR-M3G in the Korea standard nuclear plant (KSNP)[J]. EPJ Web of Conferences, 2016, 106: 03001. doi: 10.1051/epjconf/201610603001 [7] 夏春梅,梅其良,丁谦学,等. DORT程序进行RPV中子注量率计算的可靠性验证[J]. 核科学与工程,2016, 36(3): 329-334. doi: 10.3969/j.issn.0258-0918.2016.03.005 [8] CHEN J, ALPAN F A, FISCHER G A, et al. Ex-vessel neutron dosimetry analysis for Westinghouse 4-Loop XL pressurized water reactor plant using 3D parallel discrete ordinates code RAPTOR-M3G[J]. Journal of ASTM International, 2012, 9(4): 1-11. [9] U. S. Nuclear Regulatory Commission. Calculational and dosimetry methods for determining pressure vessel neutron fluence: Regulatory Guide 1.190[R]. Washington: U. S. Nuclear Regulatory Commission, 2001. [10] KIM D H, GIL C S, LEE Y O. Validation of an ENDF/B-VII. 0-based neutron and photon shielding library in MATXS-format[J]. Journal of the Korean Physical Society, 2011, 59(2): 1199-1202. [11] 张平逊,张斌,陈义学. 核反应堆屏蔽计算堆芯中子源强生成方法研究[J]. 核技术,2023, 46(5): 056003. [12] ORSI R. BOT3P-Bologna transport analysis pre-post-processors version 3.0[J]. Nuclear Science and Engineering, 2004, 146(2): 248-255. doi: 10.13182/NSE04-A2408 [13] RHOADES W A, CHILDS R L. The DORT two-dimensional discrete ordinates transport code[J]. Nuclear Science and Engineering, 1988, 99(1): 88-89. doi: 10.13182/NSE88-A23547 [14] MACFARLANE R E. TRANSX 2: a code for interfacing MATXS cross-section libraries to nuclear transport codes: LA-12312-MS[R]. Los Alamos National Laboratory, 1992. [15] Nuclear Energy Agency. Prediction of neutron embrittlement in the reactor pressure vessel: VENUS-1 and VENUS-3 benchmarks[R]. Paris: Organisation for Economic Co-Operation and Development, 2000: 239. [16] RHOADES W A, SIMPSON D B. The TORT three-dimensional discrete ordinates neutron/photon transport code (TORT version 3): ORNL/TM-13221[R]. Oak Ridge: Oak Ridge National Laboratory, 1997. [17] REMEC I, KAM F B K. H. B. Robinson-2 pressure vessel benchmark: NUREG/CR-6453[R]. Washington: US Nuclear Regulatory Commission, 1998. [18] ZHANG L, ZHANG B, LIU C, et al. Calculation of the C5G7 3-D extension benchmark by ARES transport code[J]. Nuclear Engineering and Design, 2017, 318: 231-238. doi: 10.1016/j.nucengdes.2017.04.011 -
计量
- 文章访问数: 7
- HTML全文浏览量: 6
- PDF下载量: 1
- 被引次数: 0
