Solving Multi-Dimensional Neutron Diffusion Equation Using Deep Machine Learning Technology Based on PINN Model
-
摘要: 阐述了基于物理信息指引的神经网络模型（PINN），构造深度神经网络作为试函数，将其代入中子学扩散方程形成残差，并作为机器学习的加权损失函数，进而通过深度机器学习技术逼近中子学扩散方程数值解；针对扩散方程的特点，提出了特征值方程加速收敛方法、有效增殖系数（ keff）高效并行搜索技术、学习样本网格点不均匀分布策略等创新性关键技术，并对神经网络深度、神经元数量、边界条件损失函数权重等关键参数进行了敏感性分析。验证计算结果表明，该方法具有良好的精度，提出的关键技术具有显著的成效，为中子学扩散方程的数值求解探索出了新的技术途径。
-
关键词:
- 深度机器学习 /
- 基于物理信息指引的神经网络模型（PINN） /
- 中子学扩散方程 /
- 加速收敛 /
- 有效增殖系数（k eff）
Abstract: This paper elaborates the physics-informed neural network model (PINN), constructs a deep neural network as a trial function, substitutes it into the neutron diffusion equation to form a residual, and takes it as the weighted loss function of machine learning, and then approaches the numerical solution of the neutron diffusion equation by deep machine learning technique; According to the characteristics of diffusion equation, this paper puts forward innovative key technologies such as accelerated convergence method of eigenvalue equation, efficient parallel search technology of effective multiplication coefficient (keff), learning sample grid point uneven distribution strategy, and analyzes the sensitivity of key parameters such as neural network depth, neuron number, boundary condition loss function weight and so on. The verification calculation results show that the method has good accuracy, and the proposed key technology has remarkable results, and explores a new technical approach for the numerical solution of the neutron diffusion equation. -
图 3 keff搜索散点图（沿X方向正视图）
Figure 3. keff Search Scatter Diagram (Front View Along X Direction)
图 4 边界条件损失函数权重敏感性分析
Figure 4. Sensitivity Analysis of Weight of Doundary Condition Loss Function
表 1 临界条件下稳态扩散方程计算结果
Table 1. Calculation Results of Steady-state Diffusion Equation under Critical Conditions
类型 网格点
（i）学习次
数（n）几何参
数/mσMSE,1 σ SEi,max σMSE,mc 平板 900 3500 a=1 1.4850×10−9 4.9266×10−9 4.8897×10−6 球 2000 3500 R=1 3.4875×10−10 1.9138×10−9 6.5248×10−6 圆柱 9000 5000 R=1,H=2 4.5593×10−6 4.1536×10−5 1.3897×10−5 方形 9000 5000 a=1,b=1,c=1 6.2277×10−5 7.0309×10−4 5.2182×10−5 
下载: 导出CSV
表 2 神经网络初始值敏感性分析结果
Table 2. Sensitivity Analysis Results of Iinitial Value of Neural Network
算例 网络初始
值/C0值目标C值
设定σMSE,1/10−8 学习次
数（n）学习完成
时C值1 随机/随机 无 9.9998 2405 0.015 2 随机/随机 无 9.1095 1606 0.0022 3 随机/随机 0.5 9.6124 379 0.4995 4 已训练/C0=0.01 0.5 9.1010 211 0.4996 5 已训练/C0=0.05 0.5 9.3309 55 0.4996 6 已训练/C0=0.1 0.5 9.5475 39 0.4995
下载: 导出CSV
表 3 临界条件下稳态扩散方程数值解N(
$ \vec x $ )误差分布Table 3. Error Distribution of Numerical Solution of Steady-State Diffusion Equation under Critical Conditions N(
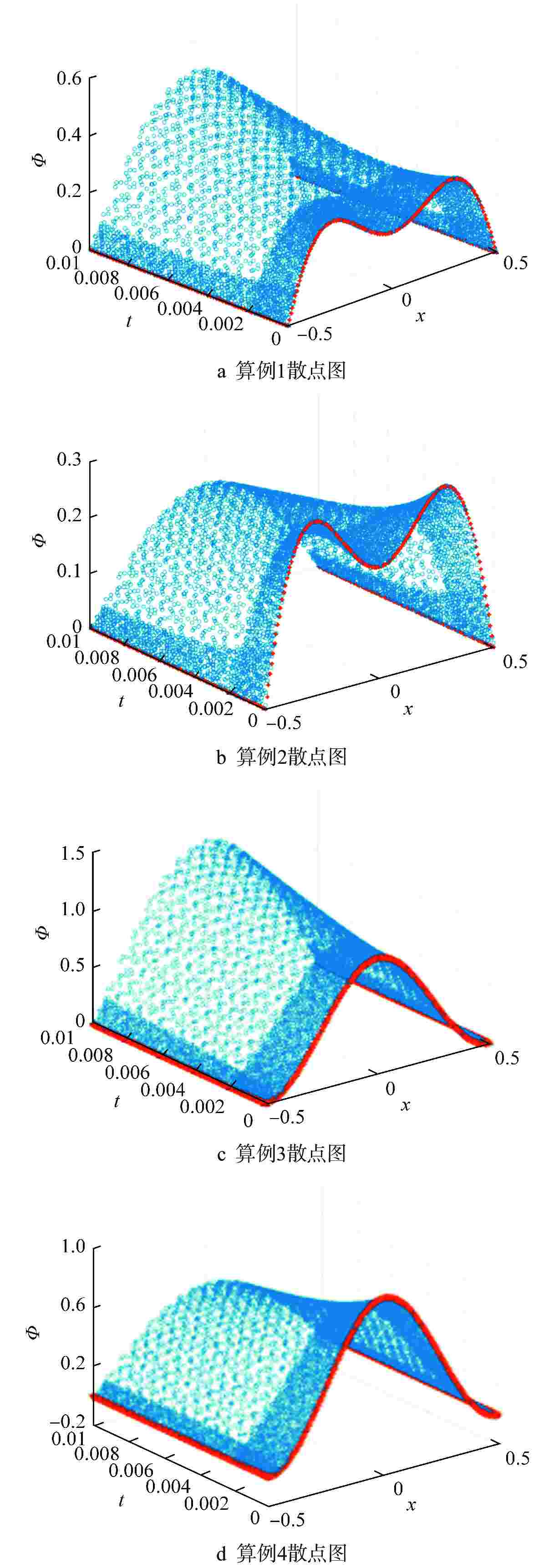
$ \vec x $ )算例 k∞ 初始条件 σMSE,1 1 1.0041 cos(π·x/a)−0.4cos(2π·x/a)−0.4 3.8005×10−7 2 1.0001 cos(π·x/a)−0.4cos(2π·x/a)−0.4 6.3758×10−7 3 1.0041 0.5[cos(2π·x/a)+1] 1.5564×10−6 4 1.0001 0.5[cos(2π·x/a)+1] 1.2230×10−6
下载: 导出CSV
表 4 keff搜索计算结果误差
Table 4. Error of keff Search Calculation Results
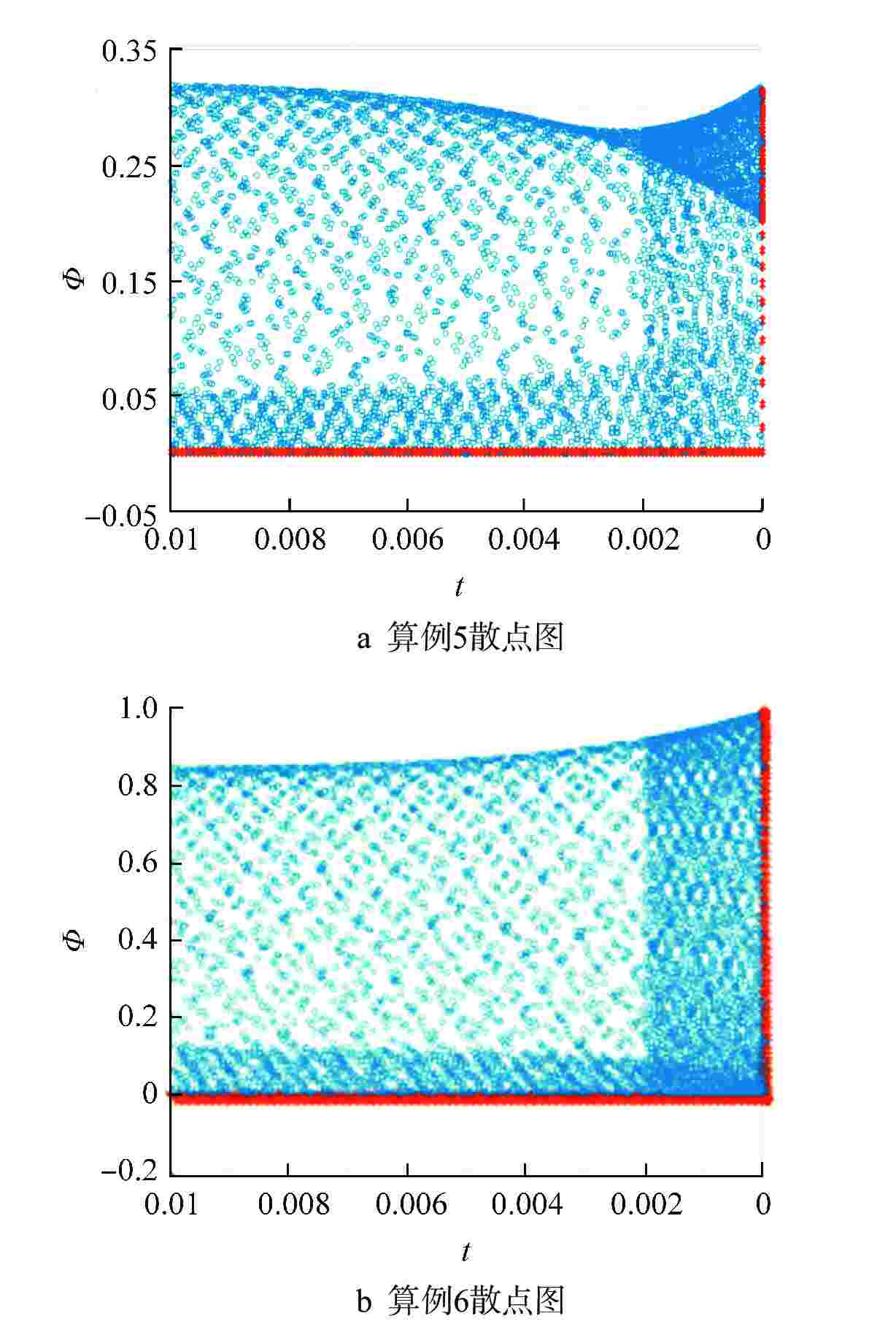
算例 算例5 算例6 k∞ 1.00410 1.00010 keff 1.00202 0.99803 初始条件 cos(π·x/a)−0.4cos
(2π·x/a)−0.40.5cos(2π·x/a)+0.5 σMSE,a 8.9108×10−7 4.4229×10−6 σMSE,b 3.8236×10−6 1.8132×10−5 σMSE,c 3.6584×10−7 8.9051×10−6 σMSE,a—N(x,t)在全域{D|−0.5≤x≤0.5,0≤t≤0.015}计算结果与解析解式（10）的均方差；σMSE,b—N(x,0.015)在{x|−0.5≤x≤0.5}上与解析解式（10）的均方差；σMSE,c—N(x,0.015)在{x|−0.5≤x≤0.5}上与平板解析解的均方差
下载: 导出CSV
表 5 网格点分布敏感性分析结果
Table 5. Sensitivity Analysis Results of Grid Point Distribution
算例 网格点分布 σMSE,1 1 D=D0，card(D0 )=2000 5.1604×10−6 2 D= D0∪DC1，card(D0)=1500，
card(DC1)=5002.8265×10−6 3 D=D0∪DC2，card(D0)=1500，
card(DC2)=5001.2731×10−6 4 D=D0∪DC2∪DB1∪DB2
card(D0)=1000，card(DC2)=500，
card(DB1)=250，card(DB2)=2508.4288×10−7 card—范围内的网格点数目
下载: 导出CSV
表 6 神经网络深度敏感性分析结果
Table 6. Sensitivity Analysis Results of Neural Network Depth
算例 l σMSE,1 1 3 1.9791×10−8 2 5 1.1187×10−8 3 9 2.6775×10−9 4 16 2.1024×10−9 5 32 1.6828×10−9
下载: 导出CSV
表 7 隐藏神经元数量敏感性分析结果
Table 7. Sensitivity Analysis Results of Number of Hidden Neurons
算例 s σMSE,1 1 5 3.6171×10−6 2 10 2.874×10−7 3 20 1.1187×10−8 4 50 1.0632×10−8 5 100 1.1001×10−8
下载: 导出CSV
表 8 不同边界条件损失函数权重训练结果
Table 8. Weight Training Results of Loss Function under Different Boundary Conditions
Pb 训练次数n σMSE,1=5×10−8 σMSE,1 =10−7 σMSE,1 =10−6 σMSE,1 =10−5 1 827 621 185 115 5 2257 367 129 50 10 2431 384 71 39 50 305 249 73 47 100 238 164 79 46 200 752 266 88 53 300 497 224 86 58 400 442 245 87 64 500 245 218 90 70
下载: 导出CSV
-
[1] 谢仲生, 曹良志, 张少泓. 核反应堆物理分析[M]. 第五版. 西安: 西安交通大学出版社, 2020: 69-90. [2] 曹良志, 谢仲生, 李云召. 近代核反应堆物理分析[M]. 北京: 中国原子能出版社, 2017: 8-209. [3] 周蜀林. 偏微分方程[M]. 北京: 北京大学出版社, 2005: 1-16. [4] 张强. 偏微分方程的有限差分方法[M]. 北京: 科学出版社, 2017: 77-114. [5] 李治平. 偏微分方程数值解讲义[M]. 北京: 北京大学出版社, 2010: 202-282. [6] GALIB S M, BHOWMIK P K, AVACHAT A V, et al. A comparative study of machine learning methods for automated identification of radioisotopes using NaI gamma-ray spectra[J]. Nuclear Engineering and Technology, 2021, 53(12): 4072-4079. doi: 10.1016/j.net.2021.06.020 [7] VAN MILLIGEN B P, TRIBALDOS V, JIMÉNEZ J A. Neural network differential equation and plasma equilibrium solver[J]. Physical Review Letters, 1995, 75(20): 3594-3597. doi: 10.1103/PhysRevLett.75.3594 [8] MAI-DUY N, TRAN-CONG T. Numerical solution of differential equations using multiquadric radial basis function networks[J]. Neural Networks, 2001, 14(2): 185-199. doi: 10.1016/S0893-6080(00)00095-2 [9] MAI-DUY N, TANNER R I. Solving high-order partial differential equations with indirect radial basis function networks[J]. International Journal for Numerical Methods in Engineering, 2005, 63(11): 1636-1654. doi: 10.1002/nme.1332 [10] MALL S, CHAKRAVERTY S. Single layer chebyshev neural network model for solving elliptic partial differential equations[J]. Neural Processing Letters, 2017, 45(3): 825-840. doi: 10.1007/s11063-016-9551-9 [11] XIE Y C, WANG Y H, MA Y, et al. Neural network based deep learning method for multi-dimensional neutron diffusion problems with novel treatment to boundary[J]. Journal of Nuclear Engineering, 2021, 2(4): 533-552. doi: 10.3390/jne2040036 [12] RAISSI M, PERDIKARIS P, KARNIADAKIS G E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707. doi: 10.1016/j.jcp.2018.10.045 [13] 刘宪高. 变分法与偏微分方程[M]. 北京: 科学出版社, 2016: 45-122. [14] HAGAN M T, DEMUTH H B, BEALE M H, et al. Neural network design[M]. ZHANG Y, trans. 2nd ed. Beijing: China Machine Press, 2018: 1-25. [15] 杨强, 张宇, 戴文渊, 等. 迁移学习[M]. 庄福振, 译. 北京: 机械工业出版社, 2020: 2-79. -
计量
- 文章访问数: 3604
- HTML全文浏览量: 595
- PDF下载量: 579
- 被引次数: 0
