Research on Solving Different Nuclear Reactor Models by Coupling Multiphysics Environment (COME) Based on Operator Spliting, Picard and JFNK Methods
-
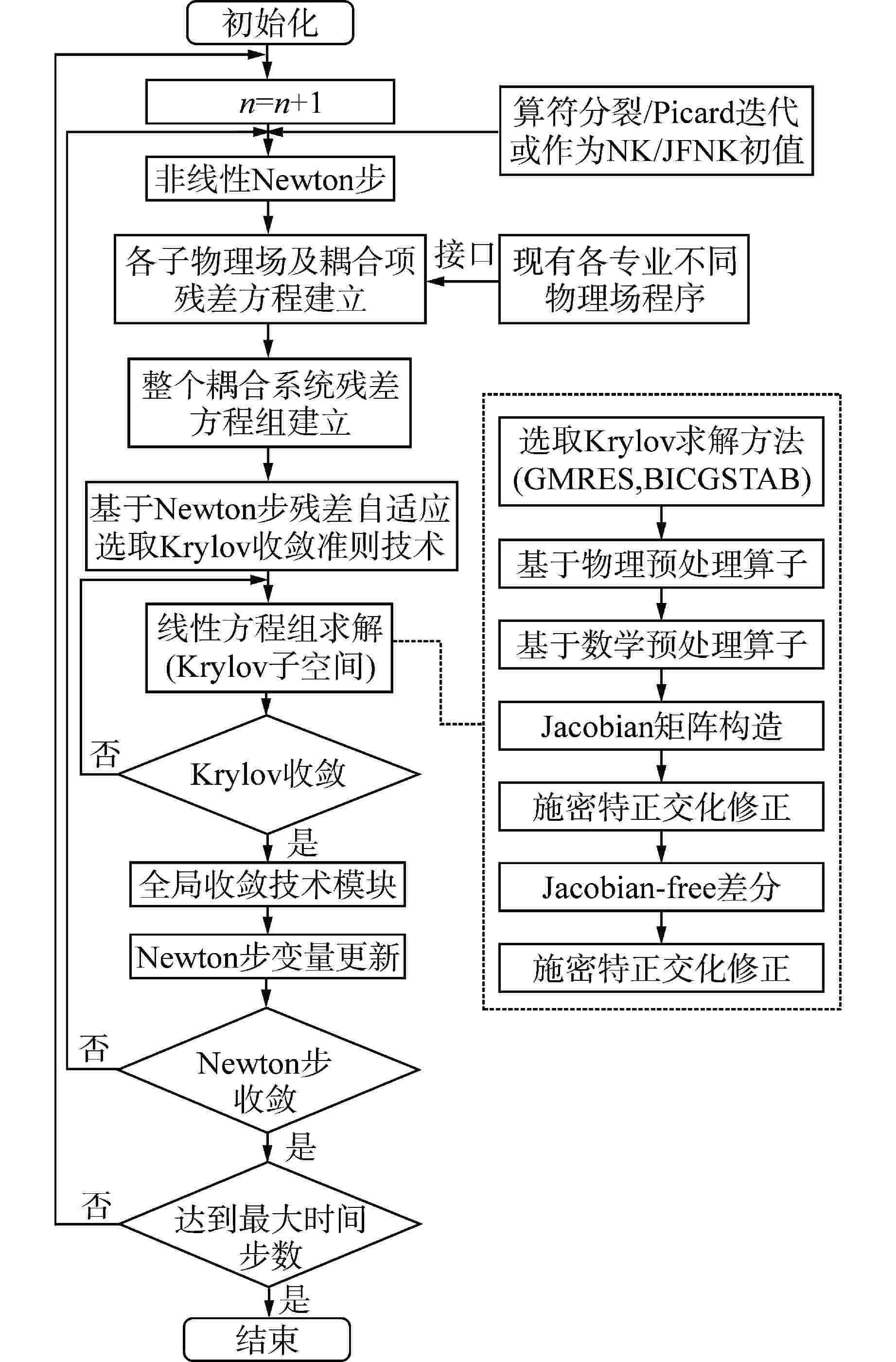
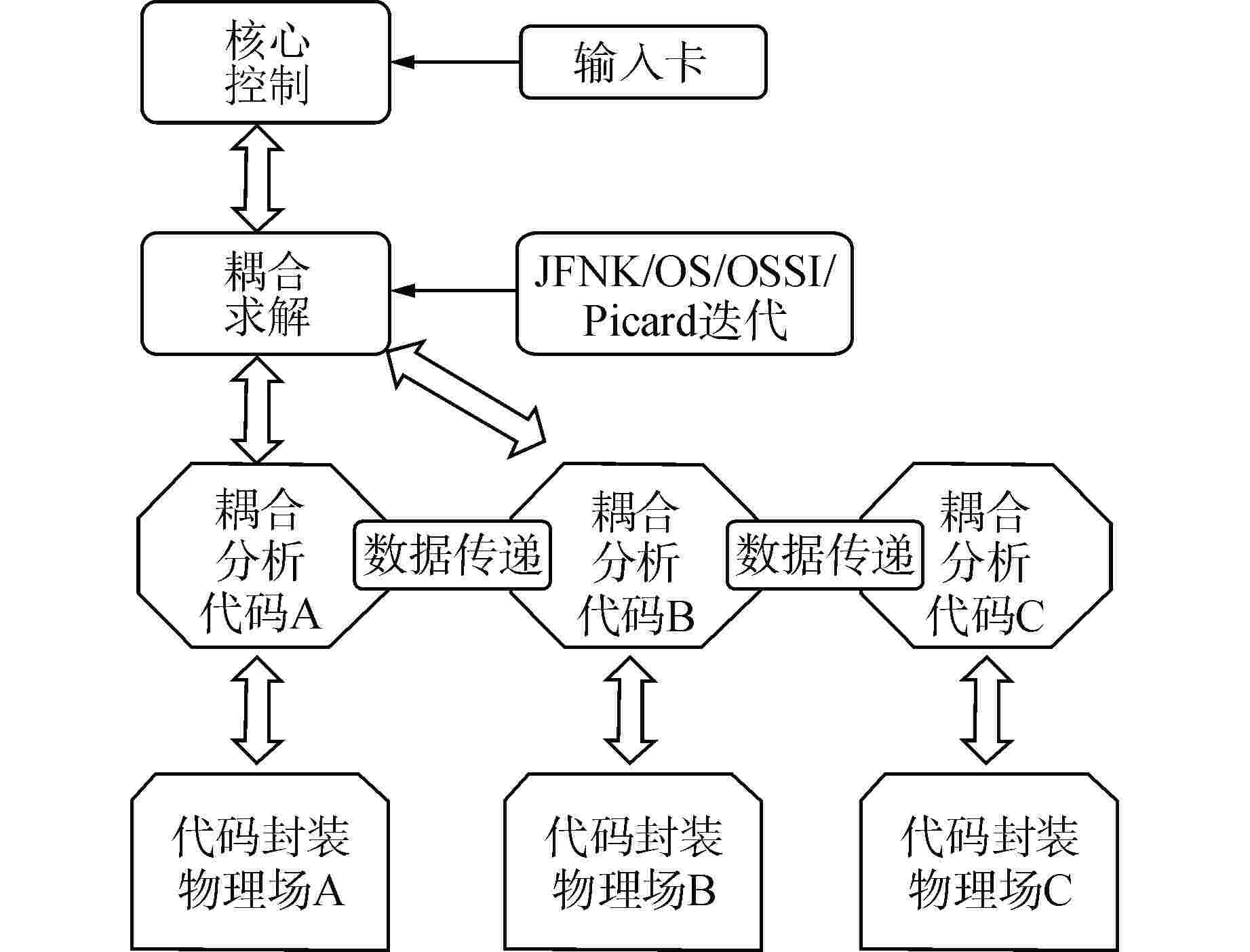
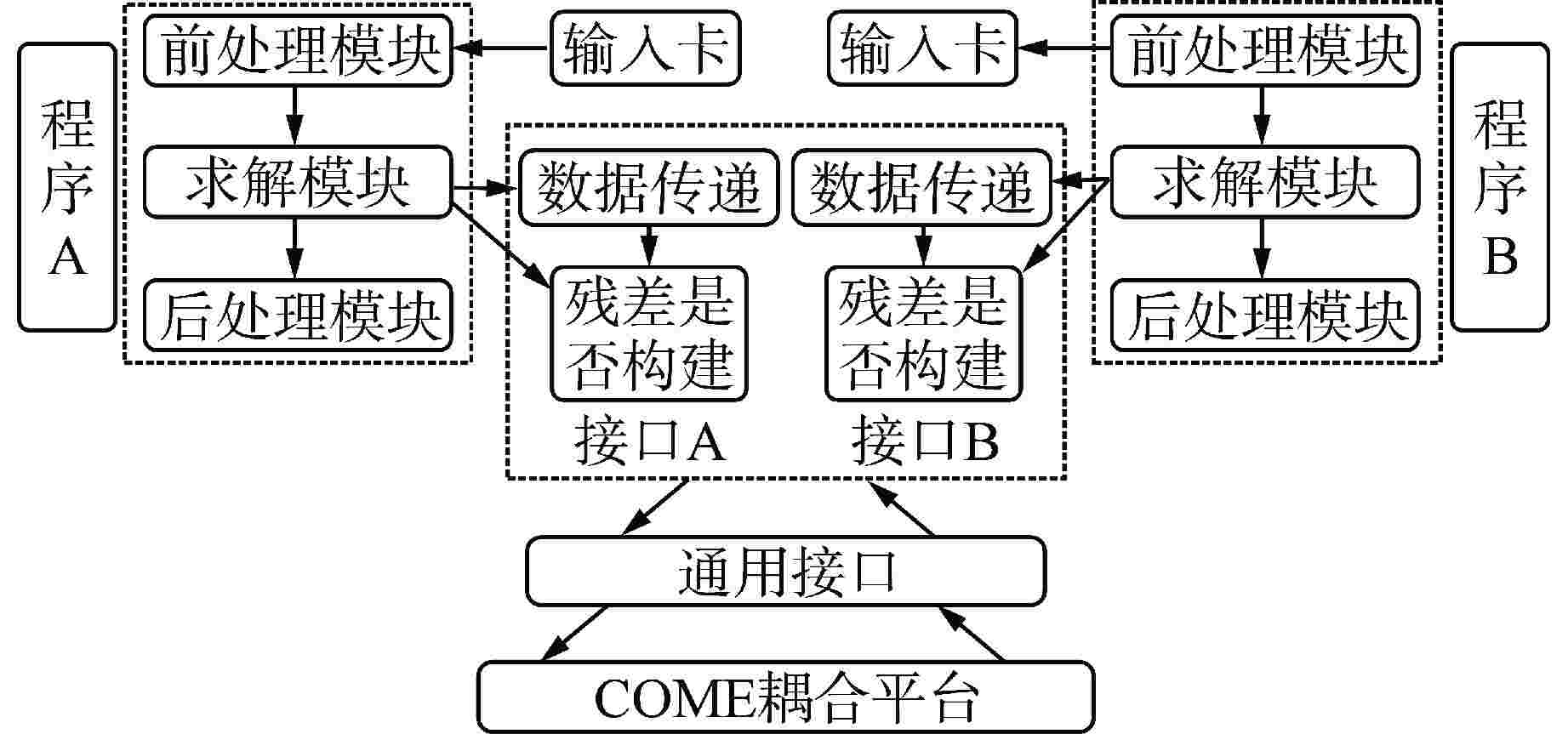
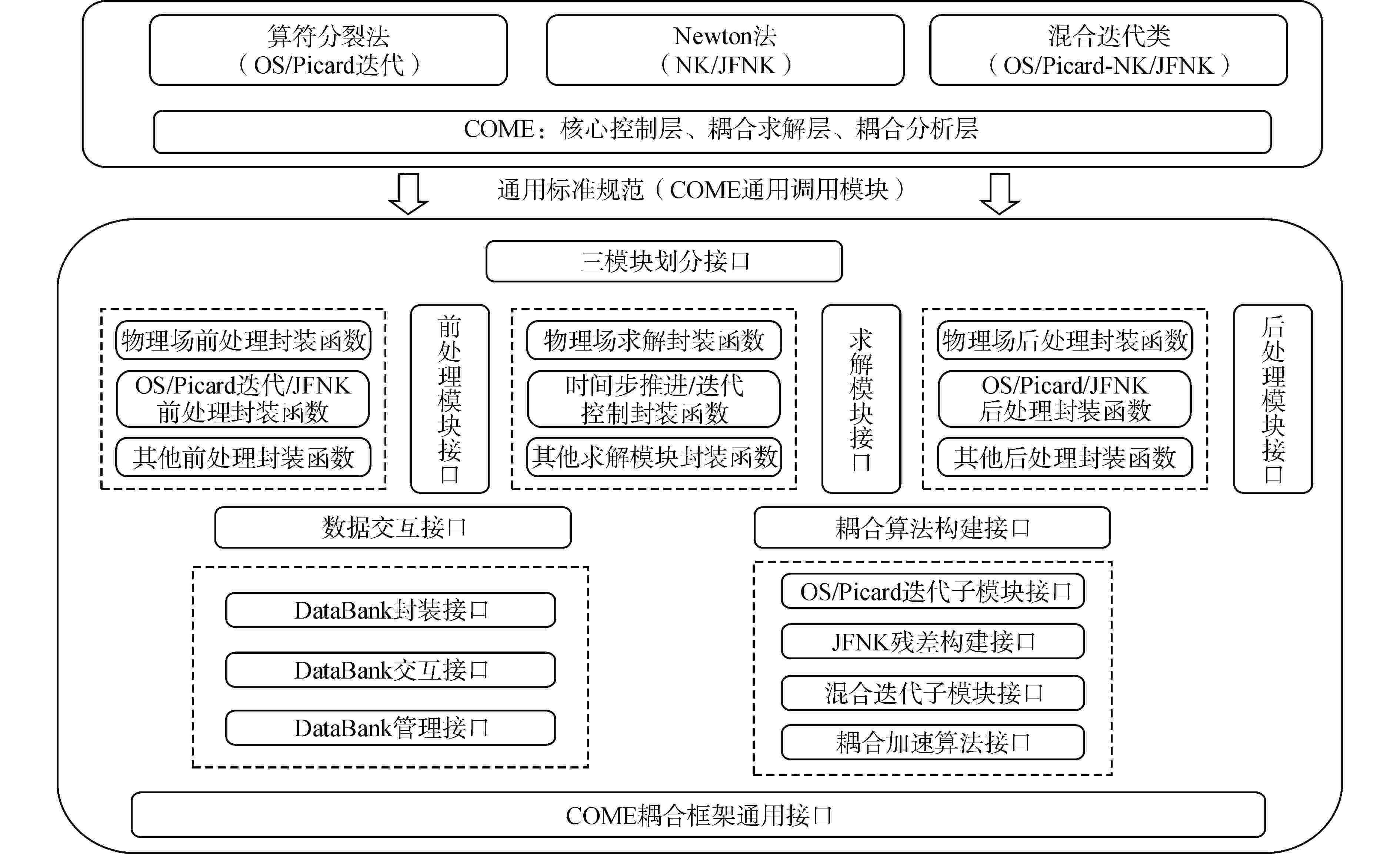
摘要: 核反应堆多物理场多尺度耦合研究是核能领域研究的难点和热点，尤其是针对核反应堆具有温度、功率、密度等物理量变化剧烈、耦合工况复杂的庞大多维、强非线性耦合系统，目前的耦合计算程序时常存在收敛慢甚至不收敛等问题，这给新一代耦合计算程序开发带来诸多挑战和困难。近年来华中科技大学虚拟反应堆耦合分析实验室基于算符分裂、Picard迭代和JFNK等多种耦合方法，初步开发了统一耦合计算框架COME。本文首先详细分析了COME中的耦合方法、总体框架和通用接口等主要特点，之后基于COME分别求解了核反应堆中子输运/扩散模型、堆芯热工子通道耦合模型、系统分析程序两相流耦合模型以及复杂物理热工耦合模型等多个耦合问题，并对比不同耦合方法的收敛性和计算效率等，为提高真实复杂多物理耦合程序的计算稳定性和收敛特性提供方法指导和开发建议。Abstract: The research on multi-physics and multi-scale coupling of nuclear reactor is challenging and prominent in the field of nuclear energy. Especially for the large-scale, multi-dimensional and strongly nonlinear coupling system with drastic changes in physical parameters such as temperature, power and density and complex coupling conditions, the current coupling calculation codes often have problems such as slow convergence or even non-convergence, which brings many challenges and difficulties to the development of next-generation coupling computational codes. In recent years, the Virtual Reactor Coupling Analysis Team (VRCAT) at Huazhong University of Science and Technology has developed a unified coupling computational framework called Coupling Multiphysics Environment (COME) based on various coupling methods, including operator splitting, Picard iteration, and Jacobian-free Newton-Krylov (JFNK). This paper first provides a detailed analysis of the main features of COME, including the coupling methods, overall framework, and common interface. Then, based on COME, several coupling problems such as neutron transport/diffusion model, core thermal sub-channel coupling model, two-phase flow coupling model within the system analysis code and complex physical-thermal coupling model are solved respectively, and the convergence and computational efficiency of different coupling methods are compared, so as to provide method guidance and development suggestions for improving the computational stability and convergence characteristics of real complex multi-physical coupling codes.
-
Key words:
- Multiphysics coupling /
- Operator splitting /
- Picard iteration /
- JFNK method /
- Coupling framework
-
图 2 JFNK流程图及关键技术
n—时间步；GMRES—广义极小残差法；BICGSTAB—稳定双共轭梯度法
Figure 2. JFNK Flowchart and Key Technologies
图 4 基于COME的各物理场程序拆分与封装
Figure 4. Split and Encapsulation of Codes Based on COME Coupled Environment
图 6 部分核反应堆堆芯中子输运/扩散模型
Figure 6. Nuclear Reactor Core Neutron Diffusion/Transport Models
图 7 堆芯热工子通道耦合模型示意图
TG—顶部格架；MG—普通交混格架；MSMG—中间横跨交混格架；BG—底部格架
Figure 7. Schematic of Sub-channel Coupled Models
图 8 全堆芯子通道耦合模型堆芯出口混合焓分布
x—横向位置；y—纵向位置
Figure 8. Distribution of Mixing Enthalpy at the Core Outlet of Full Core Subchannel Coupling Model
图 9 不同耦合方法求解全堆芯子通道耦合模型收敛性分析
Figure 9. Convergence Comparison of Different Coupling Methods for Solving Full Core Subchannel Coupling Model
图 10 JFNK求解两相流耦合模型的计算结果（网格数100）
FUD—一阶迎风离散格式；WENO3—三阶WENO离散格式；BDF1—时间一阶向后差分离散；BDF2—时间二阶向后差分离散
Figure 10. Calculation Results of JFNK Method for Solving Two-phase Flow Coupling Model (Grid Quantity: 100)
图 11 基于COME的耦合模型计算结果
Figure 11. Numerical Results of Coupled Models Predicted by COME Coupled Environment
图 12 不同耦合方法求解NEACRP 3D A1工况瞬态耦合模型的计算效率对比分析
CPU—中央处理器
Figure 12. Efficiency Comparison of Different Coupled Methods for NEACRP 3D A1 Transient Coupled Models
表 1 不同方法求解中子输运模型的计算效率对比分析
Table 1. Comparison of Computational Efficiency of Different Methods for Solving Neutron Transport Model
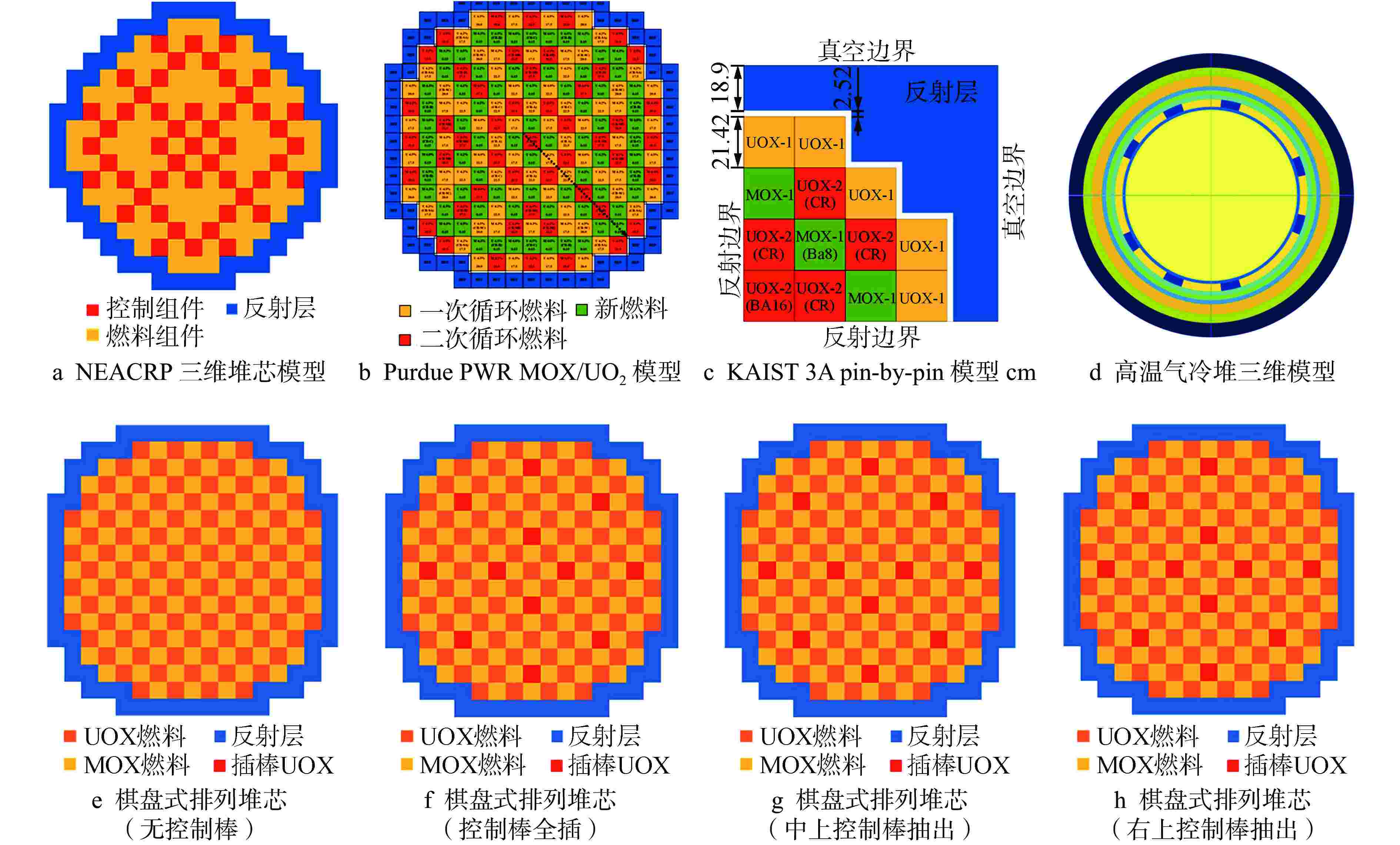
算例/模型 时间/s 加速比 comeSn_JFNK comeSn_Picard IAEA 3D（4核） 93.6 2671 28.54 KAIST 3A pin-by-pin 2D ARO 19.3 140 7.25 KAIST 3A pin-by-pin 2D ARI 15.6 157 10.06 KAIST 3A pin-by-pin 3D ARO（100核） 1961 24337 12.41 KAIST 3A pin-by-pin 3D ARI（100核） 1643 24056 14.64 棋盘式排列堆芯 pin-by-pin（2D，7G，无控制棒） 127 1956 15.40 棋盘式排列堆芯 pin-by-pin（2D，7G，控制棒全插） 91.6 1543 16.84 棋盘式排列堆芯 pin-by-pin（2D，7G，中上控制棒抽出） 170 5084 29.90 棋盘式排列堆芯 pin-by-pin（2D，7G，右上控制棒抽出） 260 7743 29.67 棋盘式排列堆芯 pin-by-pin（3D，7G，无控制棒，1024核） 1364 27937 20.48 棋盘式排列堆芯 pin-by-pin（3D，7G，控制棒全插，1024核） 1268 28616 22.57 棋盘式排列堆芯 pin-by-pin（3D，7G，中上控制棒抽出，1024核） 2203 54921 24.93 棋盘式排列堆芯 pin-by-pin（3D，7G，右上控制棒抽出，1024核） 2214 58552 26.45 C5G7-TD2-1瞬态问题 1440 50220 34.88 C5G7-TD2-2瞬态问题 1548 44820 28.95 C5G7-TD2-3瞬态问题 1368 43056 31.47 2D/3D—二维/三维；nG—能群总数 
下载: 导出CSV
表 2 不同方法求解中子扩散模型的计算效率对比分析
Table 2. Comparison of Computational Efficiency of Different Methods for Solving Neutron Diffusion Model
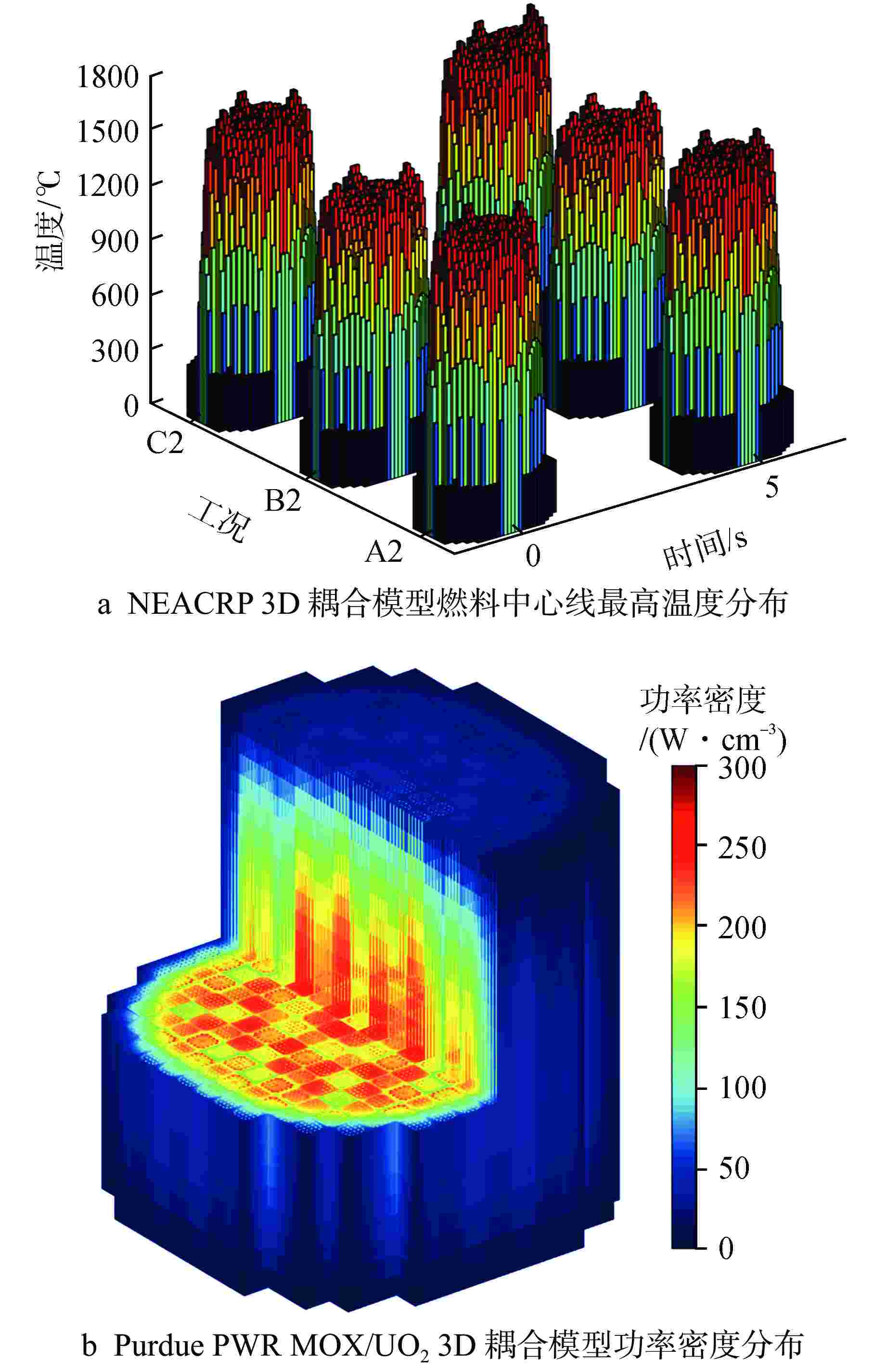
算例/模型 时间/s 加速比 NEACRP 3D A1 0.31(NEM_TNCMFD_JFNK) 1.48(NEM_TNCMFD_Picard) 4.77 NEACRP 3D A2 0.36(NEM_TNCMFD_JFNK) 2.38(NEM_TNCMFD_Picard) 6.61 NEACRP 3D B1 0.33(NEM_TNCMFD_JFNK) 1.45(NEM_TNCMFD_Picard) 4.39 NEACRP 3D B2 0.38(NEM_TNCMFD_JFNK) 1.98(NEM_TNCMFD_Picard) 5.21 NEACRP 3D C1 0.31(NEM_TNCMFD_JFNK) 1.45(NEM_TNCMFD_Picard) 4.68 Purdue PWR MOX/UO2 3D ARO 2G 0.44(NEM_TNCMFD_JFNK) 1.72(NEM_TNCMFD_Picard) 3.91 Purdue PWR MOX/UO2 3D ARO 4G 0.79(NEM_TNCMFD_JFNK) 2.78(NEM_TNCMFD_Picard) 3.52 Purdue PWR MOX/UO2 3D ARO 8G 2.13(NEM_TNCMFD_JFNK) 11.68(NEM_TNCMFD_Picard) 5.48 Purdue PWR MOX/UO2 3D ARI 2G 0.50(NEM_TNCMFD_JFNK) 1.77(NEM_TNCMFD_Picard) 3.54 Purdue PWR MOX/UO2 3D ARI 4G 0.88(NEM_TNCMFD_JFNK) 2.83(NEM_TNCMFD_Picard) 3.22 Purdue PWR MOX/UO2 3D ARI 8G 2.33(NEM_TNCMFD_JFNK) 11.84(NEM_TNCMFD_Picard) 5.08 棋盘式排列堆芯 pin-by-pin（2D，2G，无控制棒） 18.28(NEM_TNCMFD_JFNK) 66.39(NEM_TNCMFD_Picard) 3.63 棋盘式排列堆芯 pin-by-pin（2D，2G，控制棒全插） 17.72(NEM_TNCMFD_JFNK) 53.75(NEM_TNCMFD_Picard) 3.03 棋盘式排列堆芯 pin-by-pin（2D，2G，中上控制棒抽出） 26.81(NEM_TNCMFD_JFNK) 227.63(NEM_TNCMFD_Picard) 8.49 棋盘式排列堆芯 pin-by-pin（2D，2G，右上控制棒抽出） 30.81(NEM_TNCMFD_JFNK) 255.89(NEM_TNCMFD_Picard) 8.31 棋盘式排列堆芯 pin-by-pin（2D，7G，无控制棒） 70.68(NEM_TNCMFD_JFNK) 341.89(NEM_TNCMFD_Picard) 4.84 棋盘式排列堆芯 pin-by-pin（2D，7G，控制棒全插） 65.88(NEM_TNCMFD_JFNK) 283.88(NEM_TNCMFD_Picard) 4.31 棋盘式排列堆芯 pin-by-pin（2D，7G，中上控制棒抽出） 100.59(NEM_TNCMFD_JFNK) 1068.98(NEM_TNCMFD_Picard) 10.63 棋盘式排列堆芯 pin-by-pin（2D，7G，右上控制棒抽出） 167.38(NEM_TNCMFD_JFNK) 1686.73(NEM_TNCMFD_Picard) 10.08 圆柱几何下的IAEA 3D模型 0.0781(CyliNEM_JFNK) 0.4531(CyliNEM_Picard) 5.80 高温气冷堆3D（无控制棒+无吸收球） 2.03(CyliNEM_JFNK) 12.06(CyliNEM_Picard) 5.94 高温气冷堆3D（无控制棒+吸收球） 2.08(CyliNEM_JFNK) 10.05(CyliNEM_Picard) 4.83 高温气冷堆3D（控制棒插入4步+无吸收球） 2.06(CyliNEM_JFNK) 11.64(CyliNEM_Picard) 5.65 高温气冷堆3D（控制棒插入14步+无吸收球） 2.70(CyliNEM_JFNK) 27.77(CyliNEM_Picard) 10.29
下载: 导出CSV
表 3 不同耦合方法求解全堆芯子通道耦合模型计算效率对比分析
Table 3. Comparison of Computational Efficiency of Different Coupling Methods for Solving Core Subchannel Coupling Model
各组件径向
网格划分收敛精度 时间/s 加速比 原子通道程序
（Picard）JFNK耦合
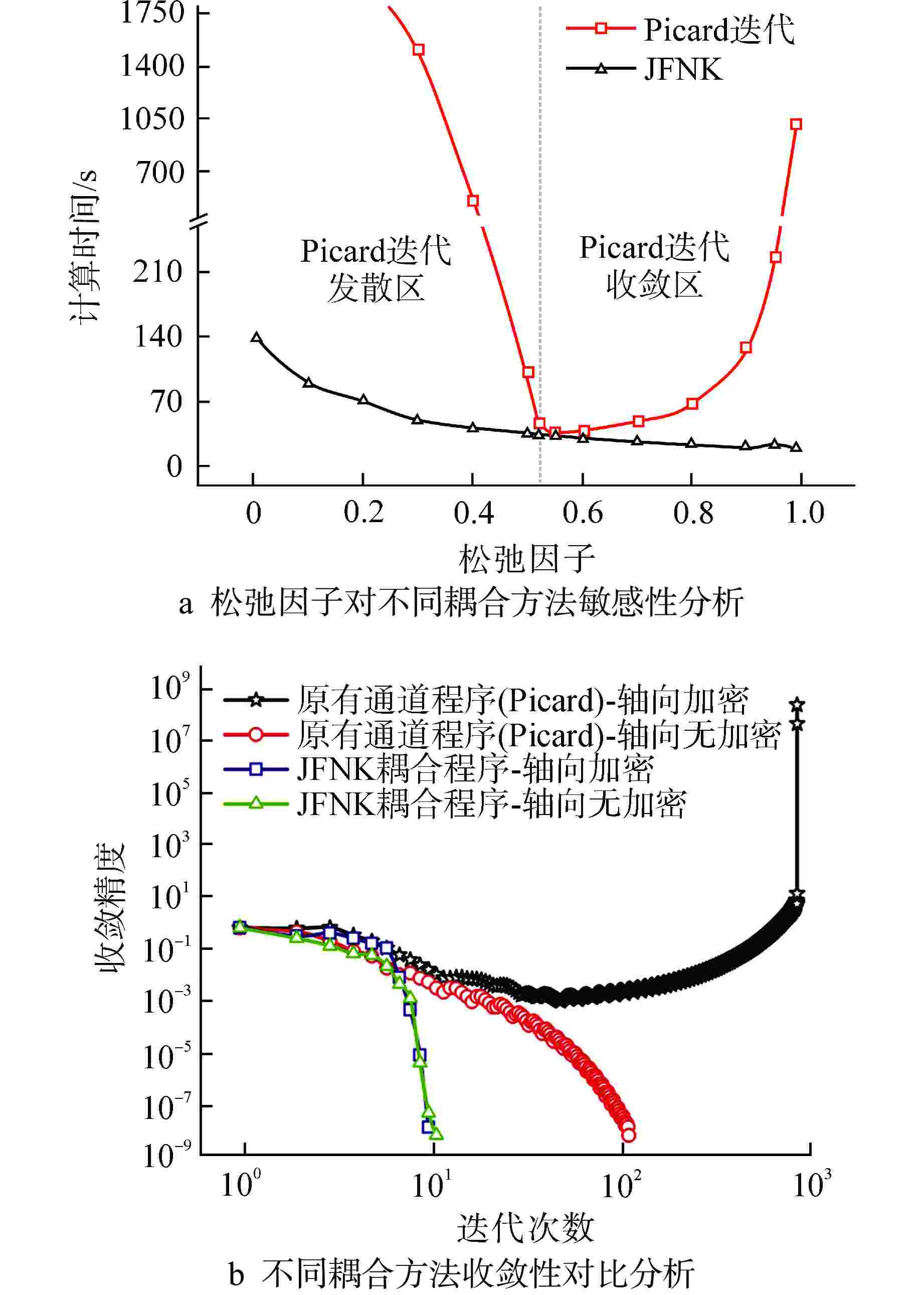
程序1×1 10−8 5.16 2.52 2.05 1×1（轴向加密） 10−8 不收敛 4.33 2×2 10−3 104.9 22.3 4.70 10−4 169.9 28.7 5.92 10−5 239.5 38.3 6.25 10−6 300.1 45.3 6.62 10−8 441.0 60.4 7.30 18×18（pin-by-pin） 10−4 4728.6 3407.6 1.38 10−5 5316.3 4018.6 1.32 10−6 6435.7 4766.8 1.35 10−8 8350.9 6658.7 1.25
下载: 导出CSV
表 4 VA+BDF2+JFNK的收敛性与效率测试（网格数200）
Table 4. Comparison of Convergence and Efficiency for VA+BDF2+JFNK Methods (Grid Quantity: 200)
稀疏结构
构造策略收敛
标准非零
元素数Newton步/
时间步Krylov数/
Newton步时间/s 方法①：初始时间步选择随机向量获得稀疏结构（只计算一次） 10−6 9977 4.12 2.69 13.34 10−10 5.58 3.83 19.94 方法②：初始时间步选择初始解向量获得稀疏结构
（只计算一次）10−6 4706
（第一次）无法收敛 10−10 方法②：初始时间步和第二时间步分别选择解向量更新稀疏结构（总共计算两次稀疏结构） 10−6 9595
（第二次）4.38 2.82 14.44 10−10 6.05 4.16 21.56 方法②：初始时间步和第二、三时间步分别选择解向量更新稀疏结构
（总共计算三次稀疏结构）10−6 9578
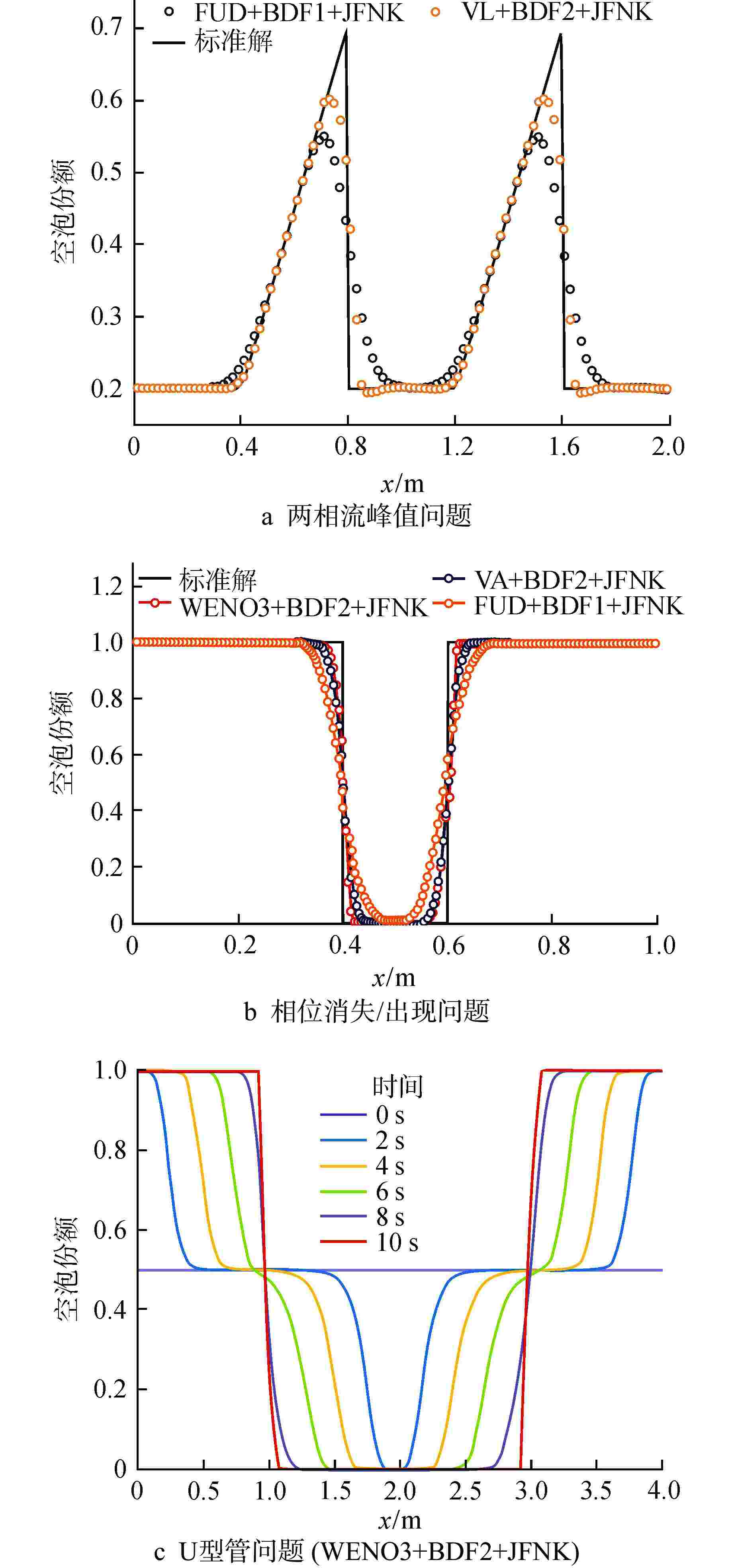
（第三次）4.89 2.70 14.84 10−10 6.78 3.81 24.24
下载: 导出CSV
表 5 WENO3+BDF2+JFNK的收敛性与效率测试（网格数200）
Table 5. Comparison of Convergence and Efficiency for WENO3+BDF2+JFNK Methods (Grid Quantity: 200)
稀疏结构构造策略 收敛
标准非零
元素数Newton步
时间步Krylov数/
Newton步时间/s 方法①：初始时间步选择随机向量获得稀疏结构
（只计算一次）10−6 10004 3.27 2.26 11.15 10−10 4.49 3.70 15.58 方法②：初始时间步选择初始解向量获得稀疏结构
（只计算一次）10−6 7487
（第一次）无法收敛 10−10 方法②：初始时间步和第二时间步分别选择解向量更新稀疏结构（总共计算两次稀疏结构） 10−6 9896
（第二次）3.30 2.26 11.70 10−10 4.55 3.89 16.59 方法②：初始时间步和第二、三时间步分别选择解向量更新稀疏结构
（总共计算三次稀疏结构）10−6 9861
（第三次）3.30 2.56 12.51 10−10 4.55 4.06 17.27
下载: 导出CSV
表 6 不同方法求解NEACRP 3D稳态耦合模型的计算效率对比分析
Table 6. Comparison of Computational Efficiency of Different Coupled Methods for NEACRP 3D Steady Coupled Models
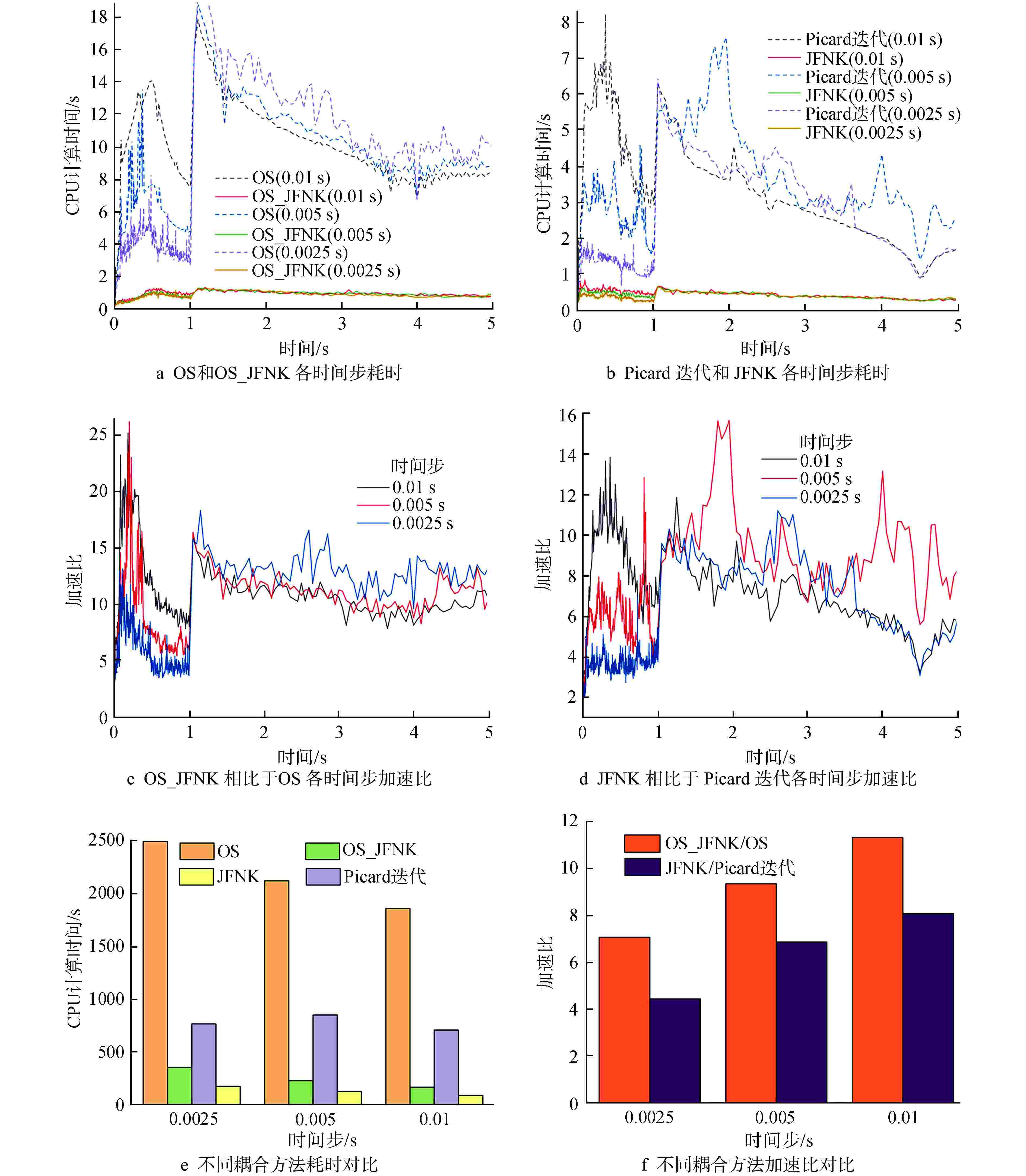
算例/模型 时间/s 加速比 JFNK Picard NEACRP 3D A2/C2 0 s时刻稳态耦合模型 2.44 6.22 2.55 NEACRP 3D A2 5 s时刻稳态耦合模型 2.44 6.25 2.56 NEACRP 3D B2 0 s时刻稳态耦合模型 2.42 6.22 2.57 NEACRP 3D B2 5 s时刻稳态耦合模型 2.48 6.25 2.52 NEACRP 3D C2 5 s时刻稳态耦合模型 2.48 6.25 2.52
下载: 导出CSV
表 7 不同方法求解Purdue PWR MOX/UO2 3D稳态耦合模型的计算效率对比分析
Table 7. Comparison of Computational Efficiency of Different Coupled Methods for Purdue PWR MOX/UO2 3D Steady Coupled Models
能群 时间/s 加速比 JFNK Picard 2G 27.64 22.11 0.80 4G 33.75 42.39 1.25 8G 52.25 123.28 2.36 8G (pin-by-pin) 3378 8261 2.45
下载: 导出CSV
-
[1] BARBER D A, MILLER R M, JOO H G, et al. A generalized interface module for the coupling of spatial kinetics and thermal-hydraulics codes: LA-UR-99-419[R]. Los Alamos: Los Alamos National Laboratory, 1999. [2] BARBER D, MILLER R M, JOO H, et al. Coupled 3D reactor kinetics and thermal-hydraulic code development activities at the U. S. Nuclear Regulatory Commission: LA-UR-99-1208[R]. Los Alamos: Los Alamos National Laboratory, 1999. [3] WEBER D P, SOFU T, PFEIFFER P A, et al. The numerical nuclear reactor for high fidelity integrated simulation of neutronic, thermal-hydraulic and thermo mechanical phenomena-project overview[C]//Proceedings of the PHYSOR 2004-The Physics of Fuel Cycles and Advanced Nuclear Systems: Global Developments. Chicago: American Nuclear Society, 2004. [4] KOCHUNAS B, JABAAY D, COLLINS B, et al. Demonstration of neutronics coupled to thermal-hydraulics for a full-core problem using COBRA-TF/MPACT: CASL-U-2014-0051-000[R]. U.S.: CASL Document, 2014. [5] PALMTAG S, CLARNO K, DAVIDSON G, et al. Coupled neutronics and thermal-hydraulic solution of a full-core PWR using VERA-CS[C]. Kyoto, Japan: Proceedings of the PHYSOR 2014- The Role of Reactor Physics Toward a Sustainable Future, 2014. [6] PÉRIN Y. Development of a multi-physics, multi-scale simulation tool for LWR safety analysis[D]. Munich: Technische Universität München, 2016. [7] GILL D F, GRIESHEIMER D P, AUMILLER D L. Numerical methods in coupled Monte Carlo and thermal-hydraulic calculations[J]. Nuclear Science and Engineering, 2017, 185(1): 194-205. doi: 10.13182/NSE16-3 [8] SENECAL J P, WEI J. A modified tightly coupled method for reactor transient simulations[C]//Proceedings of the PHYSOR 2016. Chicago: American Nuclear Society, 2016: 1690-1699. [9] HAMILTON S, BERRILL M, CLARNO K, et al. An assessment of coupling algorithms for nuclear reactor core physics simulations[J]. Journal of Computational Physics, 2016, 311: 241-257. doi: 10.1016/j.jcp.2016.02.012 [10] KNOLL D A, KEYES D E. Jacobian-free Newton-Krylov methods: a survey of approaches and applications[J]. Journal of Computational Physics, 2004, 193(2): 357-397. doi: 10.1016/j.jcp.2003.08.010 [11] GILL D F. Newton-Krylov methods for the solution of the k-eigenvalue problem in multigroup neutronics calculations[D]. Nitani Valley, Central County, Pennsylvania: Pennsylvania State University, 2009. [12] LUCAS P, VAN ZUIJLEN A H, BIJL H. Fast unsteady flow computations with a Jacobian-free Newton–Krylov algorithm[J]. Journal of Computational Physics, 2010, 229(24): 9201-9215. doi: 10.1016/j.jcp.2010.08.033 [13] WALKER E D, COLLINS B, GEHIN J C. Low-order multiphysics coupling techniques for nuclear reactor applications[J]. Annals of Nuclear Energy, 2019, 132: 327-338. doi: 10.1016/j.anucene.2019.04.022 [14] BELCOURT N, BARTLETT R A, PAWLOWSKI R P, et al. A theory manual for multi-physics code coupling in LIME: SAND2011-2195[R]. Albuquerque: Sandia National Laboratories, 2011. [15] MARTIN N, STEWART R, BAYS S. A multiphysics model of the versatile test reactor based on the MOOSE framework[J]. Annals of Nuclear Energy, 2022, 172: 109066. doi: 10.1016/j.anucene.2022.109066 [16] TURNER J A, CLARNO K, SIEGER M, et al. The virtual environment for reactor applications (VERA): design and architecture[J]. Journal of Computational Physics, 2016, 326: 544-568. doi: 10.1016/j.jcp.2016.09.003 [17] 周夏峰. 基于节块展开法的JFNK联立求解耦合系统的方法研究[M]. 北京: 清华大学出版社,2020: 194. [18] ZHOU X F. Jacobian-free Newton Krylov two-node coarse mesh finite difference based on nodal expansion method[J]. Nuclear Engineering and Technology, 2022, 54(8): 3059-3072. doi: 10.1016/j.net.2022.02.005 [19] ZHANG Y Y, ZHOU X F. Parallel Jacobian-free Newton Krylov discrete ordinates method for pin-by-pin neutron transport models[J]. Frontiers in Energy Research, 2023, 10: 1101050. doi: 10.3389/fenrg.2022.1101050 [20] 张杨奕. 并行中子输运模型的JFNK求解方法研究[D]. 武汉: 华中科技大学,2023. [21] 张杨奕,张天铖,周夏峰. 稳态及瞬态中子输运模型的JFNK求解方法研究[J]. 原子能科学技术,2024, 58(6): 1234-1241. [22] PORTER N W, MOUSSEAU V A, AVRAMOVA M N. CTF-R: a novel residual-based thermal hydraulic solver[J]. Nuclear Engineering and Design, 2019, 348: 37-45. doi: 10.1016/j.nucengdes.2019.04.006 [23] 章运山,周夏峰. 全堆芯热工子通道模型的JFNK全局求解方法研究[J]. 核动力工程,2023, 44(5): 39-46. [24] 章运山. 基于Jacobian-free Newton Krylov方法的全堆芯热工子通道耦合模型研究[D]. 武汉: 华中科技大学,2023. [25] ZHOU X F, ZHONG C M, LI Z C, et al. Preconditioned Jacobian-free Newton-Krylov fully implicit high order WENO schemes and flux limiter methods for two-phase flow models[J]. Nuclear Engineering and Technology, 2022, 54(1): 49-60. doi: 10.1016/j.net.2021.07.022 [26] ZHOU X F, ZHONG C M, ZHANG Y Y. Jacobian-free Newton Krylov two-node coarse mesh finite difference based on nodal expansion method for multiphysics coupled models[J]. Annals of Nuclear Energy, 2022, 168: 108915. doi: 10.1016/j.anucene.2021.108915 [27] ZHOU X F. Jacobian-free Newton Krylov coarse mesh finite difference algorithm based on high-order nodal expansion method for three-dimensional nuclear reactor pin-by-pin multiphysics coupled models[J]. Computer Physics Communications, 2023, 282: 108509. doi: 10.1016/j.cpc.2022.108509 [28] ZHOU X F. Operator split, Picard iteration and JFNK methods based on nonlinear CMFD for transient full core models in the coupling multiphysics environment[J]. Annals of Nuclear Energy, 2023, 183: 109669. doi: 10.1016/j.anucene.2022.109669 -
计量
- 文章访问数: 1001
- HTML全文浏览量: 73
- PDF下载量: 165
- 被引次数: 0
