Optimization of Turbulent Prandtl Numbers and RANS Models for Liquid Lead-bismuth Eutectic
-
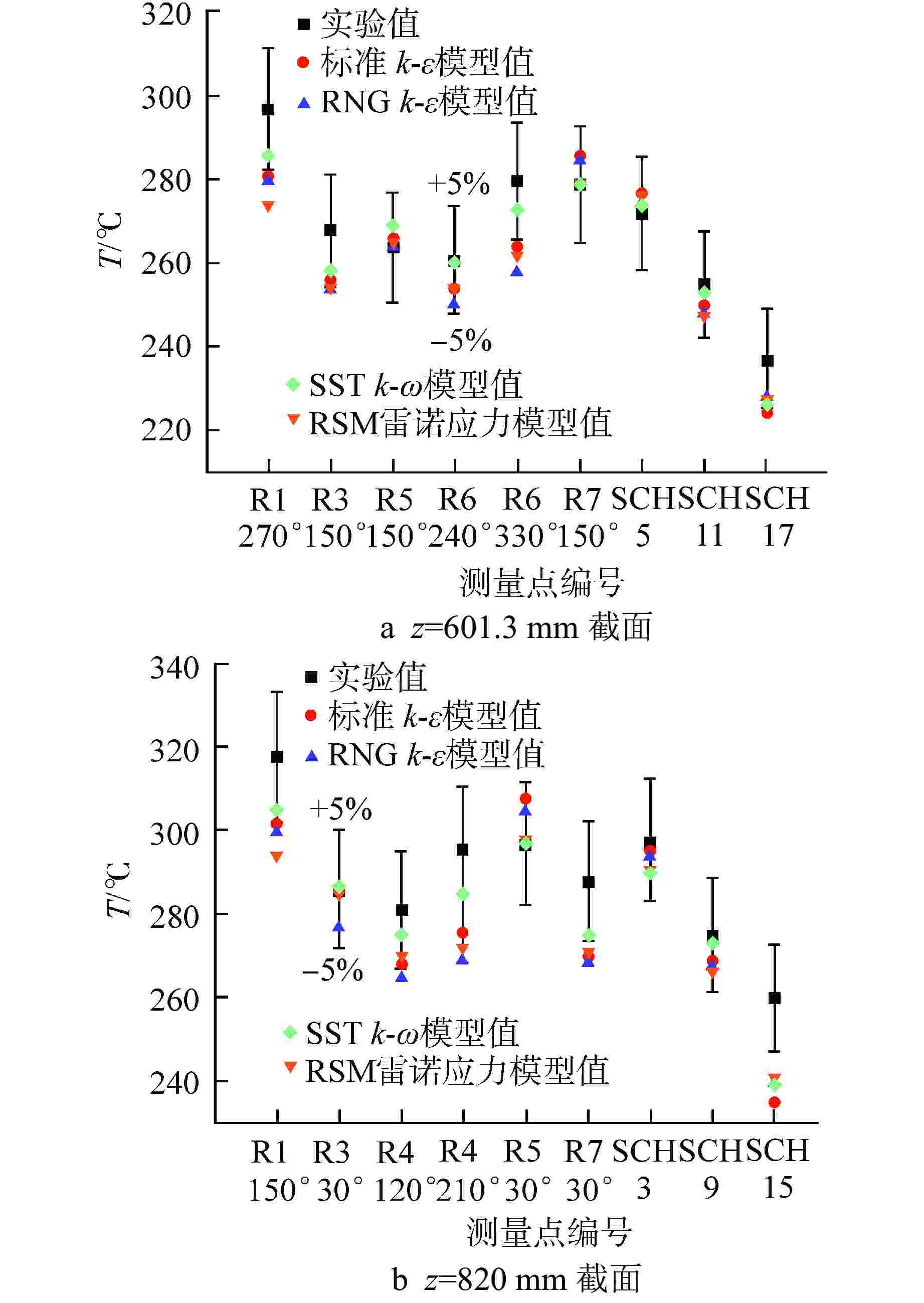
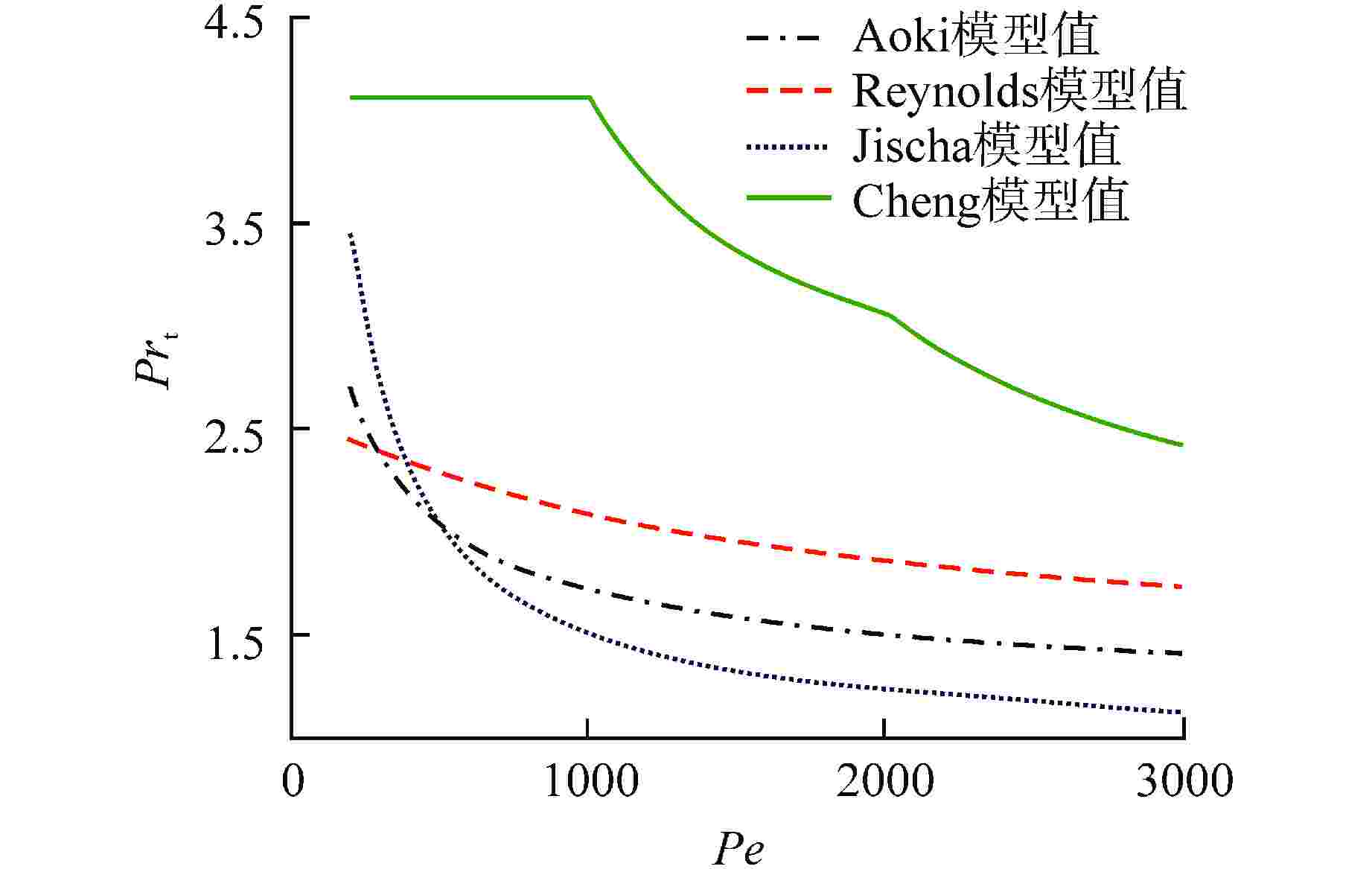
摘要: 工程上常采用RANS湍流模型进行热工水力相关的数值模拟，然而液态铅铋合金（LBE）具有独特的热物性，常规湍流普朗特数模型和RANS湍流模型对其流动与传热模拟的适用性有待研究。为更准确地描述绕丝燃料组件内LBE的流动与换热过程，本文基于大涡模拟对湍流普朗特数模型和RANS湍流模型进行优选。首先，采用四种湍流普朗特数模型对绕丝燃料组件内LBE的流动与传热过程进行大涡模拟，对比分析实验数据和模拟结果并进行模型优选。基于优选的湍流普朗特数模型，评价RANS湍流模型对LBE数值模拟的适用性和准确性。结果表明，Cheng湍流普朗特数模型和SST k-ω模型对LBE流动与传热模拟的准确性和适用性最高。
-
关键词:
- 液态铅铋合金（LBE） /
- 大涡模拟 /
- 湍流普朗特数模型 /
- RANS湍流模型 /
- 绕丝燃料组件
Abstract: In the engineering field, the RANS turbulence models are often used for thermal and hydraulic numerical simulation. However, the liquid lead-bismuth eutectic (LBE) has unique thermophysical properties, and the applicability of conventional turbulent Prandtl number models and RANS turbulence models to its flow and heat transfer simulation needs to be studied. In order to more accurately describe the flow and heat transfer process of LBE in wire-wrapped fuel assembly, the turbulent Prandtl number models and RANS turbulence models are optimized in this paper based on the large eddy simulation. First, four different turbulent Prandtl number models are used to carry out the large eddy simulation of the flow and heat transfer process of LBE in wire-wrapped fuel assembly, and the experimental data and simulation results are compared and analyzed to optimize these models. Then, based on the optimized turbulent Prandtl number model, the applicability and accuracy of the RANS turbulence models to the numerical simulation of LBE are evaluated. The results show that Cheng's turbulent Prandtl number model and SST k-ω model have the highest accuracy and applicability to the simulation of flow and heat transfer of LBE. -
图 5 LES结果与Pacio实验结果对比
R—燃料棒；SCH—子通道；角度为图4中检测点对应的角度
Figure 5. Comparison between LES Results and Pacio Experimental Results
图 6
$P{r_{\rm{t}}}$ 值与$ \varPhi $ 值散点图Figure 6.
$ P{r_{\text{t}}} $ and$ \varPhi $ Values
图 7 RANS湍流模型模拟结果与Pacio实验结果对比
Figure 7. Comparison between Simulation Results of RANS Turbulence Models and Pacio Experimental Results
表 1 模型几何参数
Table 1. Geometric Parameters of the Model
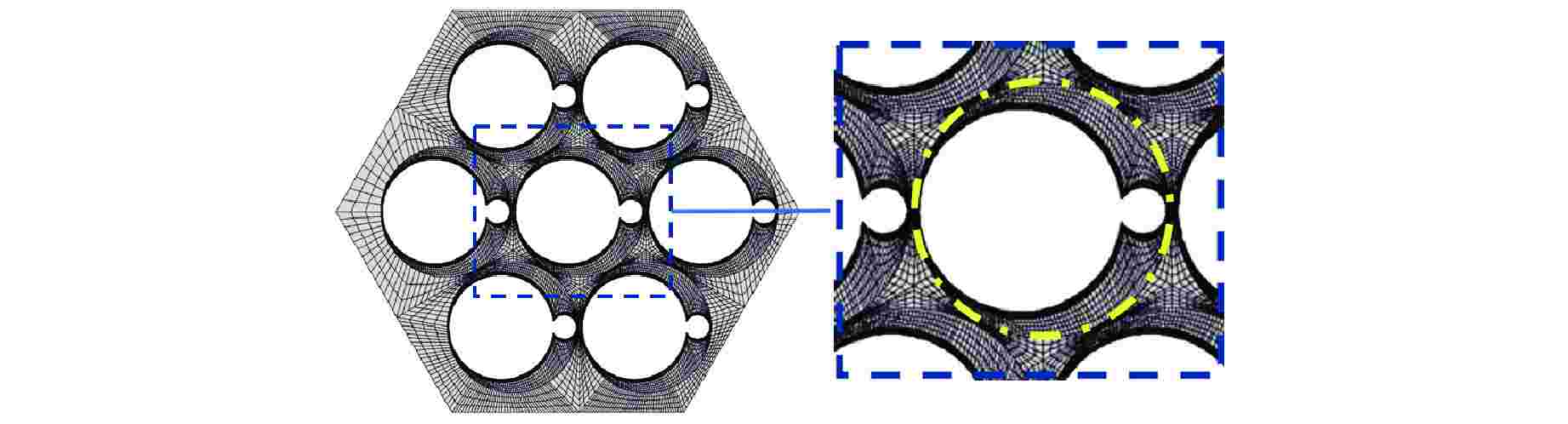
参数 数值 燃料棒根数 7 燃料棒直径/mm 8.2 燃料棒节距/mm 10.49 燃料棒长度/mm 870 绕丝直径/mm 2.2 绕丝螺距/mm 328 组件壁面对边距/mm 31.6 
下载: 导出CSV
表 2 网格无关性验证
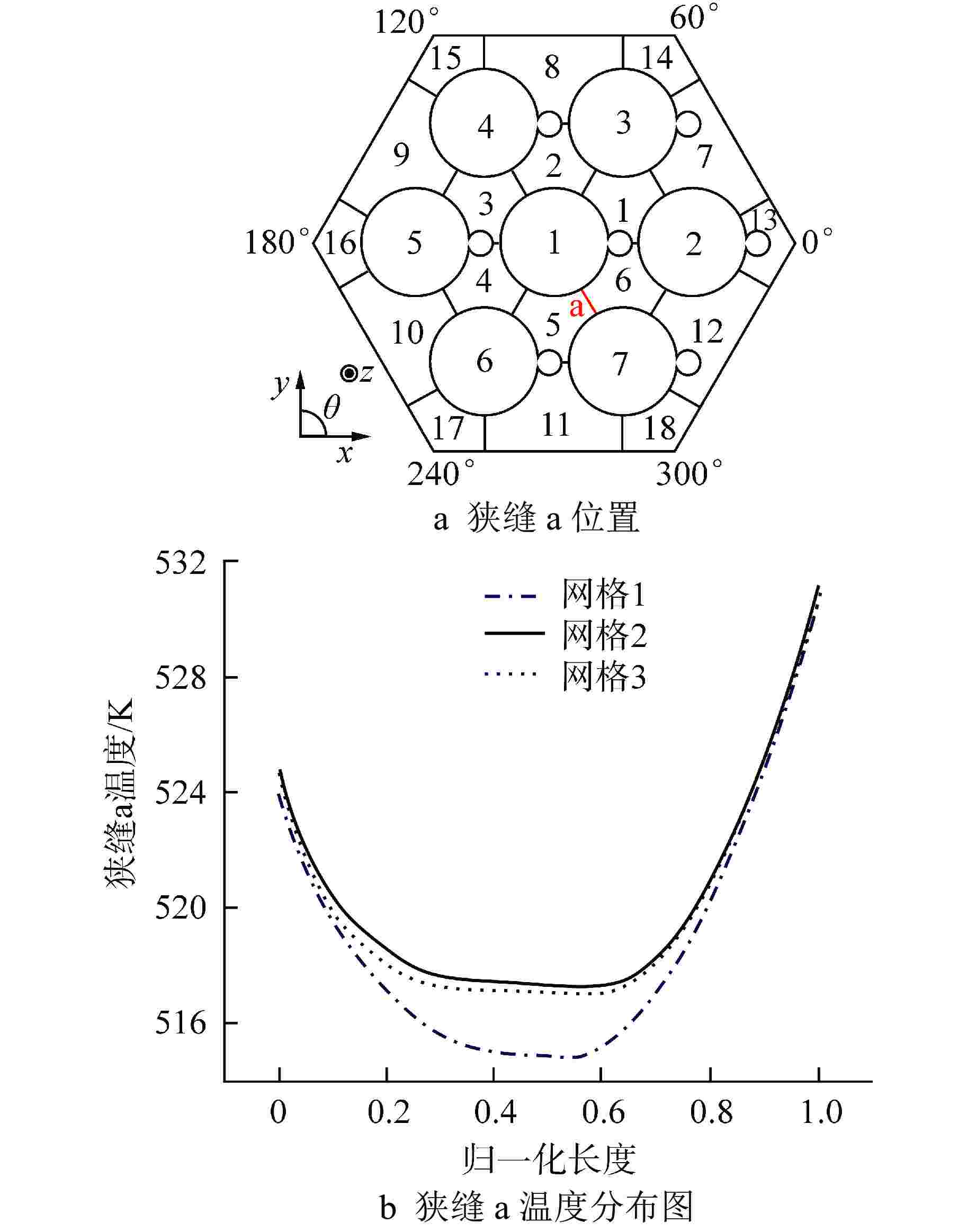
Table 2. Grid Independence Verification
网格编号 第一层网格高度/mm 边界层数 网格数 1 0.010 7 3490176 2 0.008 12 5190715 3 0.008 15 5949764
下载: 导出CSV
表 3 LES结果与Pacio实验结果拟合度
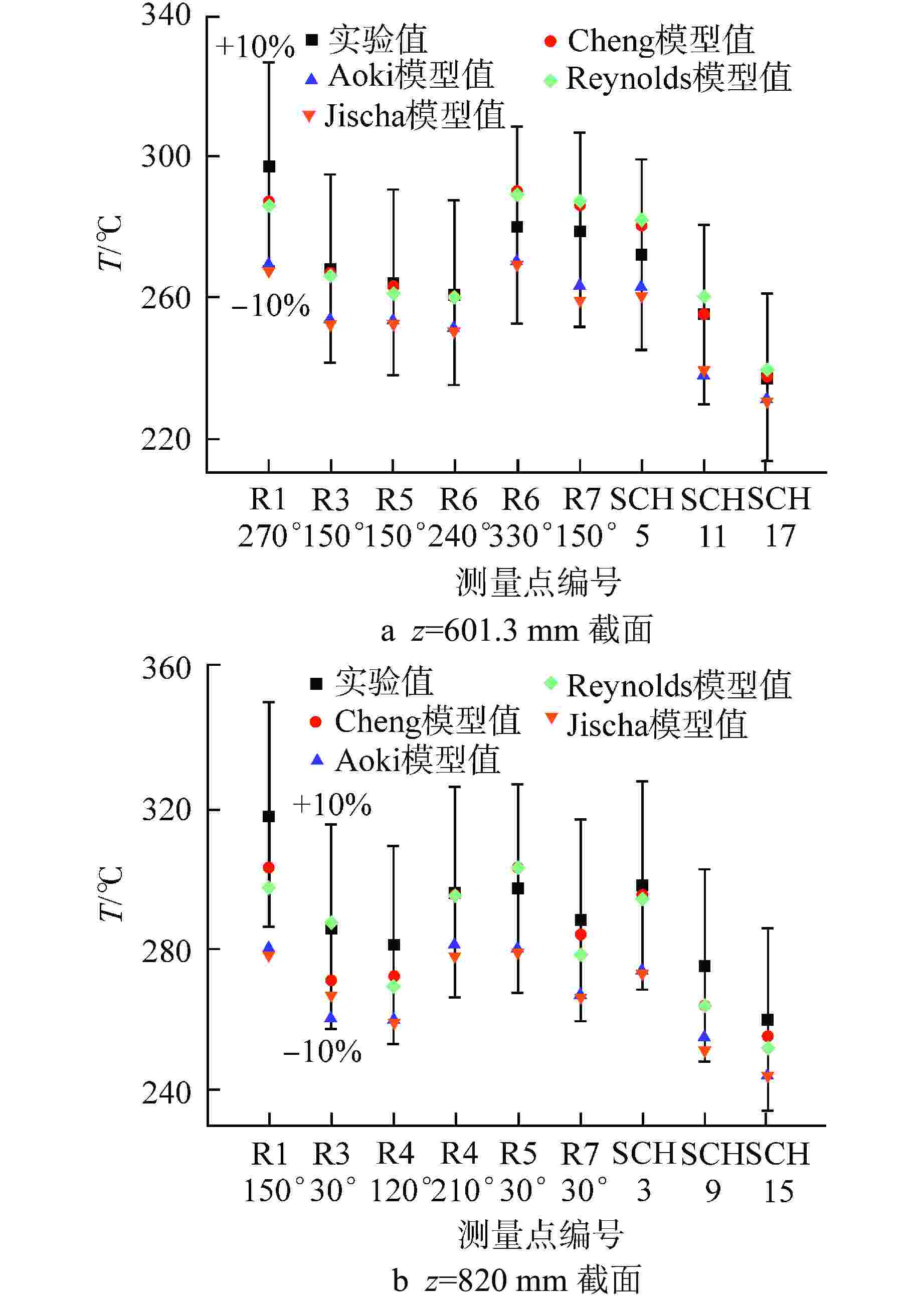
Table 3. Fitting Degree between LES Results and Pacio Experimental Results
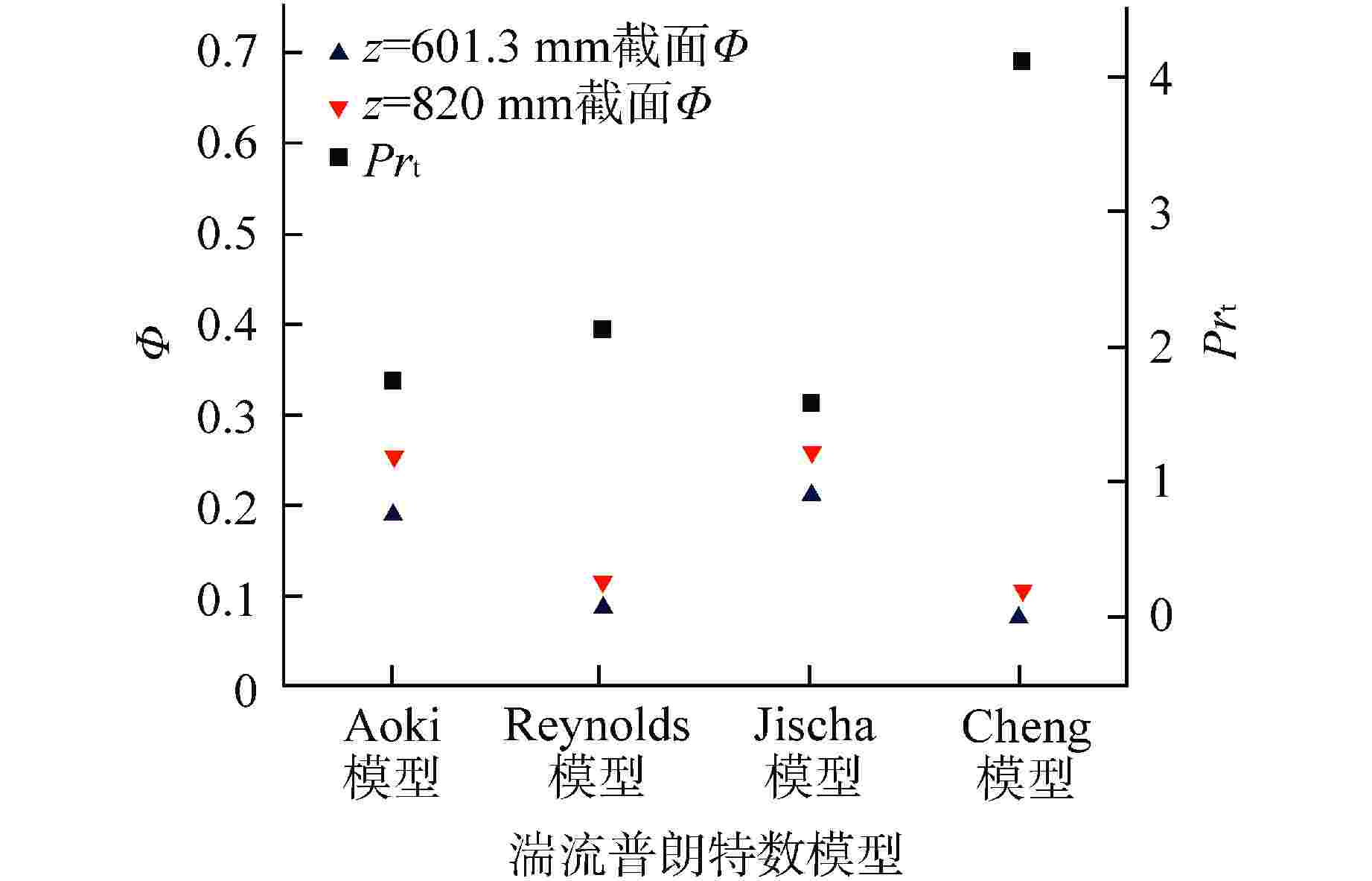
对比项 拟合度 Aoki模型 Reynolds模型 Jischa模型 Cheng模型 z=601.3 mm截面 $ {{\varTheta }_{{\text{max}}}} $ 0.2887 0.1389 0.3093 0.1250 $ {{\varTheta }_{{\text{min}}}} $ 0.1125 0.0164 0.1375 0 $ \varPhi $ 0.1901 0.0879 0.2122 0.0730 z=820 mm截面 $ {{\varTheta }_{{\text{max}}}} $ 0.3220 0.1780 0.3390 0.1744 $ {{\varTheta }_{{\text{min}}}} $ 0.1563 0.0104 0.1856 0.0104 $ \varPhi $ 0.2531 0.1115 0.2600 0.1024
下载: 导出CSV
表 4 RANS湍流模型模拟结果与Pacio实验结果拟合度
Table 4. Fitting Degree between Simulation Results of RANS Turbulence Models and Pacio Experimental Results
对比项 拟合度 标准k-ε
模型RNG k-ε
模型SST k-ω
模型RSM
模型z=601.3 mm截面 $ {{\varTheta }_{{\text{max}}}} $ 0.3514 0.2750 0.2703 0.2703 $ {{\varTheta }_{{\text{min}}}} $ 0.0313 0 0 0 $ \varPhi $ 0.1689 0.1713 0.1172 0.1699 z=820 mm截面 $ {{\varTheta }_{{\text{max}}}} $ 0.4167 0.3333 0.3500 0.3167 $ {{\varTheta }_{{\text{min}}}} $ 0.0116 0.0408 0 0.0103 $ \varPhi $ 0.1895 0.1907 0.1424 0.1763
下载: 导出CSV
-
[1] DUPONCHEEL M, BRICTEUX L, MANCONI M, et al. Assessment of RANS and improved near-wall modeling for forced convection at low Prandtl numbers based on LES up to Reτ = 2000[J]. International Journal of Heat and Mass Transfer, 2014, 75: 470-482. doi: 10.1016/j.ijheatmasstransfer.2014.03.080 [2] NATESAN K, SUNDARARAJAN T, NARASIMHAN A, et al. Turbulent flow simulation in a wire-wrap rod bundle of an LMFBR[J]. Nuclear Engineering and Design, 2010, 240(5): 1063-1072. doi: 10.1016/j.nucengdes.2009.12.025 [3] SAGAUT P. Large eddy simulation for incompressible flows. An introduction[J]. Measurement Science and Technology, 2001, 12(10): 1745-1746. [4] AOKI S. A consideration on the heat transfer in liquid metal[J]. Bulletin of the Tokyo Institute of Technology, 1963, 54: 63-73. [5] REYNOLDS A J. The prediction of turbulent Prandtl and Schmidt numbers[J]. International Journal of Heat and Mass Transfer, 1975, 18(9): 1055-1069. doi: 10.1016/0017-9310(75)90223-9 [6] JISCHA M, RIEKE H B. About the prediction of turbulent Prandtl and Schmidt numbers from modeled transport equations[J]. International Journal of Heat and Mass Transfer, 1979, 22(11): 1547-1555. doi: 10.1016/0017-9310(79)90134-0 [7] CHENG X, TAK N I. Investigation on turbulent heat transfer to lead–bismuth eutectic flows in circular tubes for nuclear applications[J]. Nuclear Engineering and Design, 2006, 236(4): 385-393. doi: 10.1016/j.nucengdes.2005.09.006 [8] PACIO J, DAUBNER M, FELLMOSER F, et al. Experimental study of heavy-liquid metal (LBE) flow and heat transfer along a hexagonal 19-rod bundle with wire spacers[J]. Nuclear Engineering and Design, 2016, 301: 111-127. doi: 10.1016/j.nucengdes.2016.03.003 [9] PACIO J, DAUBNER M, FELLMOSER F, et al. Corrigendum to "Experimental study of heavy-liquid metal (LBE) flow and heat transfer along a hexagonal 19-rod bundle with wire spacers"[Nucl. Eng. Des. 301 (2016) 111-127][J]. Nuclear Engineering and Design, 2021, 371: 110928. doi: 10.1016/j.nucengdes.2020.110928 [10] FAZIO C, SOBOLEV V P, AERTS A, et al. Handbook on lead-bismuth eutectic alloy and lead properties, materials compatibility, thermal-hydraulics and technologies[M]. France: Organisation for Economic Co-operation and Development, 2015: 91. [11] GAJAPATHY R, VELUSAMY K, SELVARAJ P, et al. CFD investigation of helical wire-wrapped 7-pin fuel bundle and the challenges in modeling full scale 217 pin bundle[J]. Nuclear Engineering and Design, 2007, 237(24): 2332-2342. doi: 10.1016/j.nucengdes.2007.05.003 [12] JEONG J H, SONG M S, LEE K L. CFD investigation of three-dimensional flow phenomena in a JAEA 127-pin wire-wrapped fuel assembly[J]. Nuclear Engineering and Design, 2017, 323: 166-184. doi: 10.1016/j.nucengdes.2017.08.008 [13] FEI C, HUAI X L, CAI J, et al. Investigation on the applicability of turbulent-Prandtl-number models for liquid lead-bismuth eutectic[J]. Nuclear Engineering and Design, 2013, 257: 128-133. doi: 10.1016/j.nucengdes.2013.01.005 [14] MERZARI E, FISCHER P, YUAN H, et al. Benchmark exercise for fluid flow simulations in a liquid metal fast reactor fuel assembly[J]. Nuclear Engineering and Design, 2016, 298: 218-228. doi: 10.1016/j.nucengdes.2015.11.002 -
计量
- 文章访问数: 344
- HTML全文浏览量: 82
- PDF下载量: 84
- 被引次数: 0
