Study on Monte Carlo Importance Sampling Method Based on Unstructured Mesh
-
摘要: 为改善传统的依赖结构网格有限差分离散纵标（SN）程序确定粒子重要性分布的一致性共轭驱动重要抽样（CADIS）方法的建模和计算精度，以进一步提高其处理复杂几何深穿透问题的能力，本文开发了基于SN-间断有限元方法（DFEM）的并行三维非结构网格中子-光子耦合输运计算程序NECP-SUN，并将其作为共轭求解器与蒙特卡罗程序NECP-MCX耦合，研究并实现了全自动的非结构网格CADIS方法。对HBR-2基准题和中国聚变工程试验堆（CFETR）环向场磁体线圈盒快中子注量率的计算结果表明：较传统CADIS方法，非结构网格CADIS方法对复杂几何的适应性更强，取得的结果相对统计偏差更低、更接近实测值；较直接蒙特卡罗计算，非结构网格CADIS方法的品质因子（FOM）提高了1~3个量级。因此，本文研究的非结构网格CADIS方法能够较好地处理复杂几何深穿透问题。
-
关键词:
- 中子输运计算 /
- 蒙特卡罗方法 /
- 一致性共轭驱动重要抽样（CADIS）方法 /
- 非结构网格
Abstract: In order to improve the modeling and calculation accuracy of the traditional Consistent Adjoint Driven Importance Sampling (CADIS) method that relies on structural-mesh finite-difference discrete ordinate (SN) code to determine the importance distribution of particles to further enhance its capability of dealing with complex-geometric deep-penetration problems, a fully automatic unstructured-mesh CADIS method is studied and implemented in this paper, parallel three-dimensional unstructured-mesh neutron-photon-coupled transport code NECP-SUN based on SN method and discontinuous finite element method (DFEM) is developed and embedded into the Monte Carlo code NECP-MCX as adjoint transport solver. The numerical results of the calculations of the HBR-2 benchmark and the fast-neutron fluence rate of the toroidal field coil boxes in the Chinese Fusion Engineering Test Reactor (CFETR) show that the unstructured-mesh CADIS method has stronger adaptability to complex geometry than the traditional CADIS method, and the results obtained are relatively lower in relative statistical error and closer to the measurements; the figure of merit (FOM) is increased by 1~3 orders than that of direct Monte Carlo simulation. Therefore, the unstructured-mesh CADIS method studied in this paper can better handle deep-penetration problems with complex geometry. -
图 5 HBR-2基准题的结构网格模型及非结构网格模型
Figure 5. The Structural-Mesh Model and Unstructured-Mesh Model of HBR-2 Benchmark
图 6 局部加密前后的中子剂量仪区域网格
Figure 6. Mesh of Radiometric Monitor with/without Local Refinement
图 7 CFETR 22.5°扇段的CAD模型及非结构网格建模
Figure 7. CAD Model and Unstructured Mesh of CFETR 22.5° Sector
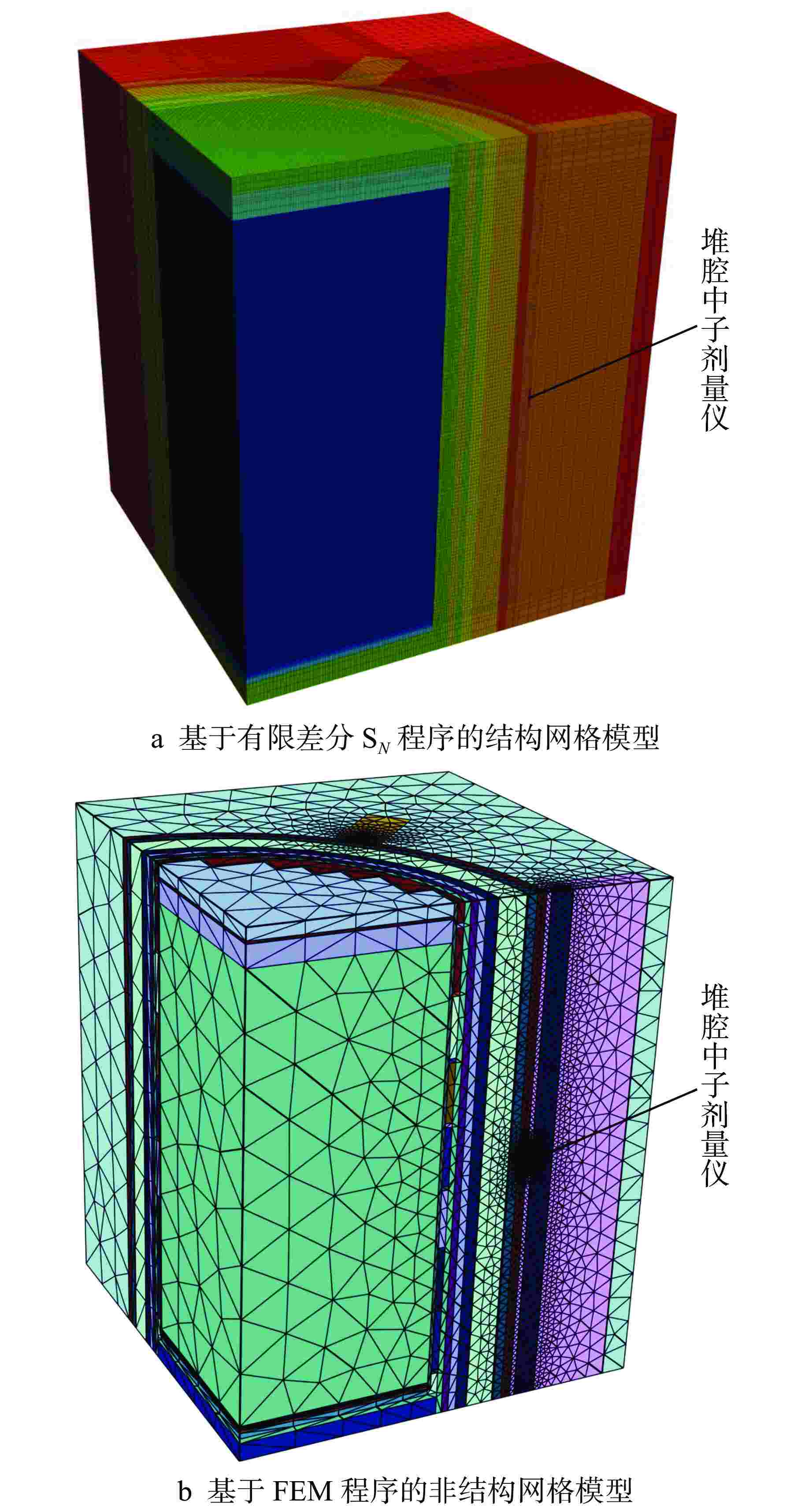
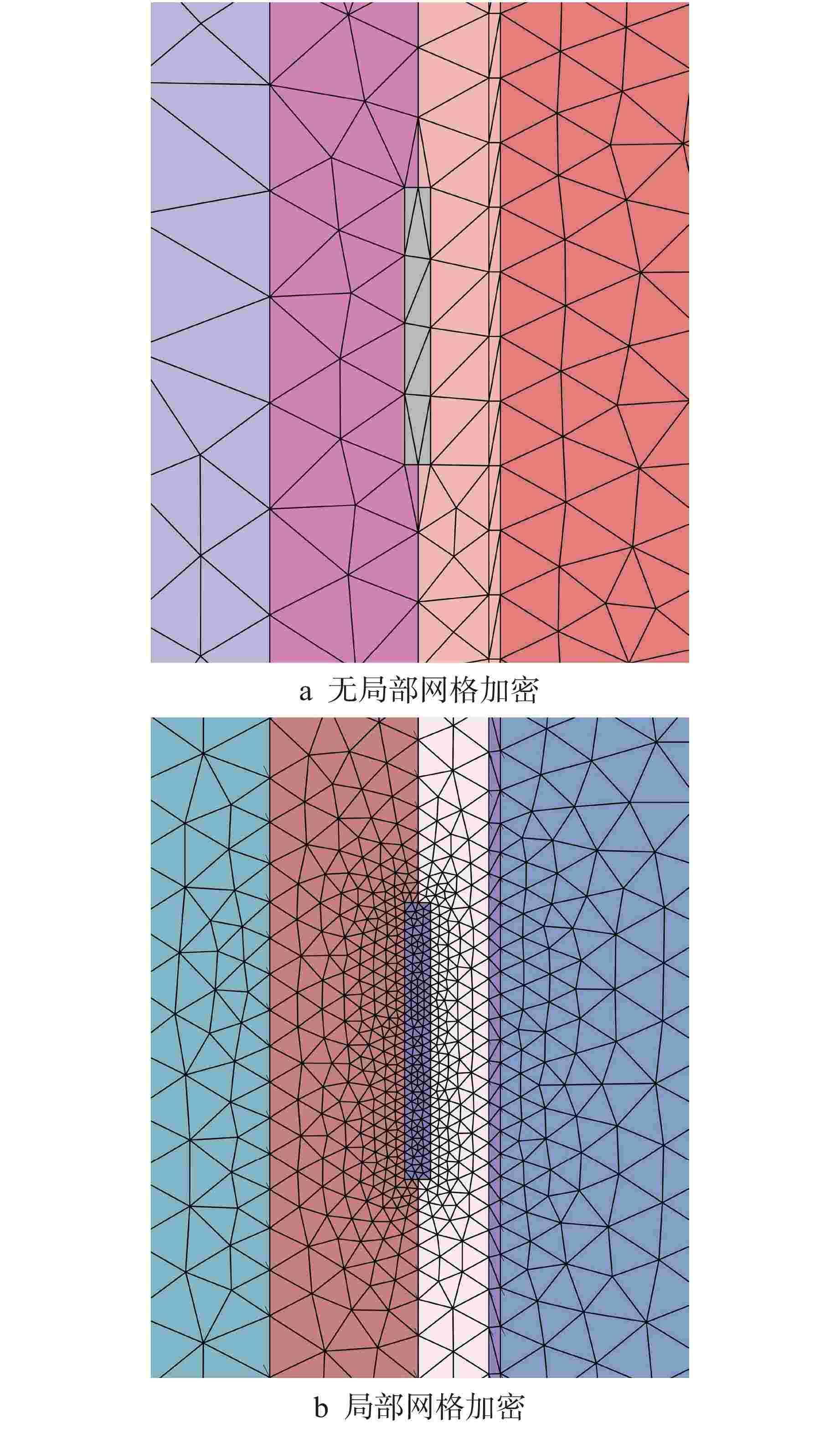
表 1 网格剖分参数及网格数量
Table 1. Subdivision Parameters of Meshes and Number of Meshes
网格剖分方式 全局剖分 目标区域局部加密 最小尺寸/cm 0.5 2 最大尺寸/cm 48 48 目标区域尺寸/cm 0.5 网格数量 1113428 246357 
下载: 导出CSV
表 2 堆腔中子剂量仪各反应道的比活度及其C/E值
Table 2. Specific Activities and C/E of each Reaction Channel of Radiometric Monitor in Reactor Cavity
计算方法 统计量 237Np(n,f)137Cs 238U(n,f)137Cs 58Ni(n,p)58Co 54Fe(n,p)54Mn 46Ti(n,p)46Sc 63Cu(n,α)60Co 实验测量 比活度/(Bq·mg−1) 2.24×101 8.51×10−1 1.96×102 8.71×100 3.31×100 2.65×10−1 MCX 比活度/(Bq·mg−1) 2.00×101 9.24×10−1 6.86×101 7.89×10−1 无计数 无计数 C/E 0.89 1.09 0.35 0.09 无计数 无计数 MCX_Hydra 比活度/(Bq·mg−1) 1.64×101 6.63×10−1 2.29×102 1.00×101 4.63×100 3.25×10−1 C/E 0.73 0.78 1.17 1.15 1.40 1.23 MCX_SUN 比活度/(Bq·mg−1) 1.60×101 6.40×10−1 2.20×102 9.65×100 4.27×100 2.87×10−1 C/E 0.71 0.75 1.12 1.11 1.29 1.08 MCX_SUN_Fine 比活度/(Bq·mg−1) 1.60×101 6.39×10−1 2.17×102 9.51×100 4.26×100 2.84×10−1 C/E 0.71 0.75 1.11 1.09 1.29 1.07
下载: 导出CSV
表 3 堆腔中子剂量仪各反应道的相对统计偏差和FOM
Table 3. Relative Statistical Errors and FOM of each Reaction Channel of Radiometric Monitor in Reactor Cavity
计算方法 统计量 237Np(n,f)137Cs 238U(n,f)137Cs 58Ni(n,p)58Co 54Fe(n,p)54Mn 46Ti(n,p)46Sc 63Cu(n,α)60Co MCX 相对统计偏差/% 37.86 97.97 85.49 99.99 100 100 FOM 1.57×10−2 2.35×10−3 3.08×10−3 2.25×10−3 无实际意义 无实际意义 MCX_Hydra 相对统计偏差/% 0.21 0.74 1.04 1.18 2.23 4.05 FOM 4.97×101 4.09×100 2.08×100 1.60×100 4.52×10−1 1.36×10−1 MCX_SUN 相对统计偏差/% 0.49 1.05 1.48 1.73 1.57 2.47 FOM 5.14×100 1.13×100 5.65×10−1 4.14×10−1 5.02×10−1 2.03×10−1 MCX_SUN_Fine 相对统计偏差/% 0.32 0.74 0.86 0.98 1.74 3.25 FOM 1.37×101 2.52×100 1.89×100 1.43×100 4.59×10−1 1.31×10−1
下载: 导出CSV
表 4 环向场磁体线圈盒快中子注量率及其相对统计偏差和FOM
Table 4. Value, Relative Statistic Errors and FOM of Fast-Neutron Fluence Rate of Toroidal Field Coil Boxes
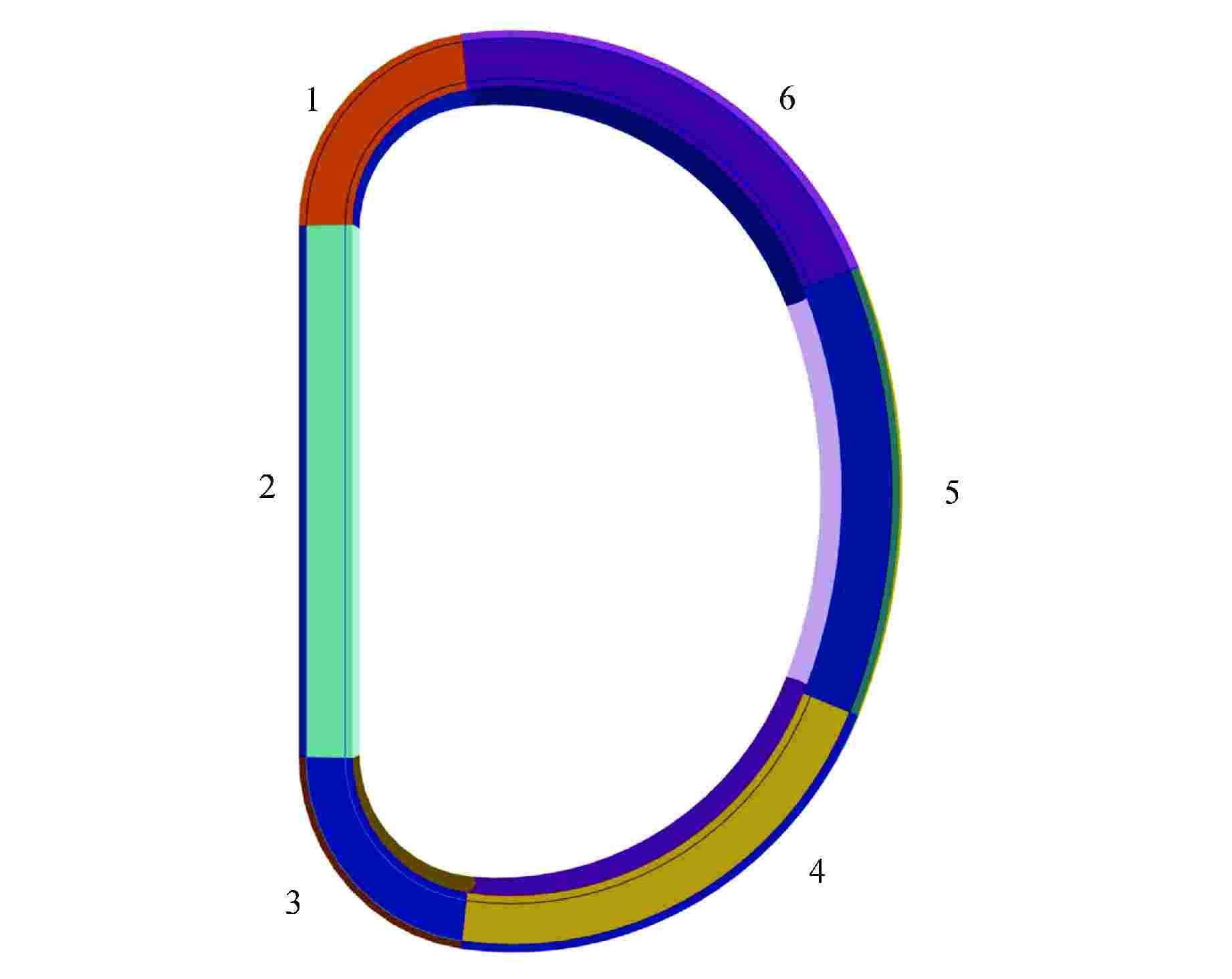
计算方法 统计量 线圈盒1 线圈盒2 线圈盒3 线圈盒4 线圈盒5 线圈盒6 MCX_9 快中子注量率/(cm−2·s−1) 1.116×107 1.154×107 4.363×106 6.899×106 1.479×106 3.565×106 相对统计偏差/% 40.16 28.93 47.70 28.36 47.73 39.61 FOM 5.334×10−3 1.028×10−2 3.781×10−3 1.069×10−2 3.775×10−3 5.483×10−3 MCX_12 快中子注量率/(cm−2·s−1) 1.474×107 2.083×107 8.541×106 8.172×106 1.746×106 3.362×106 相对统计偏差/% 5.76 36.08 5.90 2.73 5.60 4.41 FOM 1.857×10−3 4.737×10−5 1.773×10−3 8.275×10−3 1.966×10−3 3.165×10−3 MCX_SUN 快中子注量率/(cm−2·s−1) 1.563×107 2.120×107 9.087×106 7.878×106 1.814×106 3.166×106 相对统计偏差/% 3.77 2.89 4.02 3.30 9.00 3.19 FOM 1.267×10−1 2.157×10−1 1.114×10−1 1.657×10−1 2.221×10−2 1.764×10−1
下载: 导出CSV
-
[1] 曹良志, 谢仲生, 李云召. 近代核反应堆物理分析[M]. 北京: 中国原子能出版社, 2017: 310-313. [2] MUNK M, SLAYBAUGH R N. Review of hybrid methods for deep-penetration neutron transport[J]. Nuclear Science and Engineering, 2019, 193(10): 1055-1089. doi: 10.1080/00295639.2019.1586273 [3] WAGNER J C, HAGHIGHAT A. Automated variance reduction of Monte Carlo shielding calculations using the discrete ordinates adjoint function[J]. Nuclear Science and Engineering, 1998, 128(2): 186-208. doi: 10.13182/NSE98-2 [4] MOSHER S W, JOHNSON S R, BEVILL A M, et al. ADVANTG—an automated variance reduction parameter generator: ORNL/TM-2013/416 Rev. 1[R]. Oak Ridge: Oak Ridge National Laboratory, 2015. [5] PEPLOW D E. Monte Carlo shielding analysis capabilities with MAVRIC[J]. Nuclear Technology, 2011, 174(2): 289-313. doi: 10.13182/NT174-289 [6] ALWIN J L, SPENCER J B, FAILLA G A. Criticality accident alarm system analysis using MCNP6.2 constructive solid geometry/unstructured mesh hybrid[Z]. 2019. [7] WAREING T A, MCGHEE J M, MOREL J E. ATTILA: a three-dimensional, unstructured tetrahedral mesh discrete ordinates transport code[J]. Transactions of the American Nuclear Society, 1996, 75: 146-147. [8] DOMINESEY K A, KOWAL P J, EUGENIO J A, et al. Scientific workflows for MCNP6 and proteus within the neams workbench[C]//International Conference on Physics of Reactors: Transition to a Scalable Nuclear Future. Cambridge: EDP Sciences, 2021: 06052. [9] WARNER P, DE OLIVEIRA C R E. Validation of the 3D finite element transport theory code EVENT for shielding applications[J]. Journal of Nuclear Science and Technology, 2000, 37(S1): 466-470. [10] MIAO J X, FANG C, WAN C H, et al. Development and preliminary application of deterministic code NECP-FISH for neutronics analysis of fusion-reactor blanket[J]. Annals of Nuclear Energy, 2022, 169: 108943. doi: 10.1016/j.anucene.2021.108943 [11] REED W H, HILL T R. Triangular mesh methods for the neutron transport equation: Technical Report LA-UR-73-479[R]. Mex: Los Alamos Scientific Laboratory, 1973. [12] HE Q M, ZHENG Q, LI J, et al. NECP-MCX: A hybrid Monte-Carlo-Deterministic particle-transport code for the simulation of deep-penetration problems[J]. Annals of Nuclear Energy, 2021, 151: 107978. doi: 10.1016/j.anucene.2020.107978 [13] REMEC I, KAM F B K. H. B. Robinson-2 pressure vessel benchmark: NUREG/CR-6453; ORNL/TM-13204[R]. Washington: US Nuclear Regulatory Commission, 1998. [14] XU L F, CAO L Z, ZHENG Y Q, et al. Development of a new parallel SN code for neutron-photon transport calculation in 3-D cylindrical geometry[J]. Progress in Nuclear Energy, 2017, 94: 1-21. doi: 10.1016/j.pnucene.2016.09.005 [15] EL-MEHALAWI M, MILLER R A. A database system of mechanical components based on geometric and topological similarity. Part I: representation[J]. Computer-Aided Design, 2003, 35(1): 83-94. doi: 10.1016/S0010-4485(01)00177-4 -
计量
- 文章访问数: 1727
- HTML全文浏览量: 66
- PDF下载量: 82
- 被引次数: 0
