Research on Prediction of Subcooled Flow Boiling CHF for Spiral Flow Based on Machine Learning
-
摘要: 过冷沸腾广泛应用于以国际热核聚变实验堆(ITER)为代表的高热流冷却场合。本文聚焦高热流、螺旋流动条件下水的过冷沸腾临界热流密度(CHF)的预测方法,建立了该类工况下的过冷沸腾CHF实验数据库。选用了4种典型机器学习模型:反向传播(BP)神经网络、遗传算法( GA )-BP神经网络、 径向基函数(RBF)神经网络和极限学习机(ELM);利用传统的经验关联式和新兴的机器学习方法对螺旋流动过冷沸腾CHF进行预测研究。经与实验数据库对比,结果表明,相关机器学习模型能够有效预测螺旋流动过冷沸腾CHF,其预测性能相较于传统的经验关联式有大幅提升,其中ELM模型预测效果最优,平均绝对误差和均方根误差分别为2.79%和4.22%。研究成果为高热流螺旋流动过冷沸腾CHF的准确预测提供了新途径。
-
关键词:
- 临界热流密度(CHF) /
- 过冷沸腾 /
- 机器学习 /
- 传热 /
- 两相流
Abstract: Subcooled boiling is widely used in cooling applications with high heat fluxes represented by International Thermonuclear Experimental Reactor (ITER). In this paper, predictions on the critical heat flux (CHF) of subcooled water boiling under high heat flux and swirl flow conditions are focused and a database of subcooled boiling CHF is established. Machine learning methods are applied, in which four typical machine learning models are adopted, namely Back Propagation (BP) neural network, Genetic Algorithm (GA)-BP neural network, Radial Basis Function (RBF) neural network and Extreme Learning Machine (ELM). The results indicate that machine learning models can effectively predict subcooled boiling CHF with swirling flow, and the prediction performances are obviously promoted, comparing with traditional empirical correlations. Among typical machine learning models, the ELM model possesses the best performance, with the MAE and RMSE are equal to 2.79% and 4.22%, respectively. The results provide a new path to making accurate predictions on the CHF for subcooled boiling under high heat flux and swirling flow conditions.-
Key words:
- Critical heat flux (CHF) /
- Subcooled boiling /
- Machine learning /
- Heat transfer /
- Two-phase flow
-
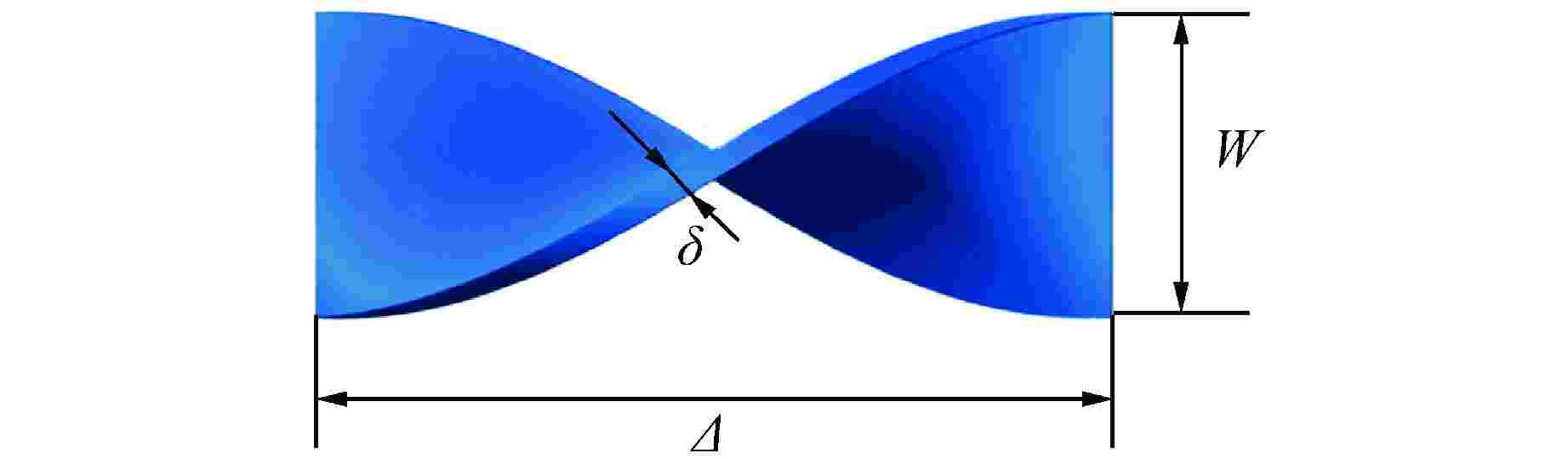
表 1 高热流条件下内插扭带管的过冷水流动沸腾CHF数据
Table 1. CHF Data for Subcooled Water Flow in Twisted-Tape Tubes under High Heat Fluxes
参数名 参数值 Yan[11] Gambill[18] Tong[19] Hata-Masuzaki[20] Araki[21] Boscary[22] Dedov[9-10] 内径d/mm 9 6.3 2.42~6.53 6 7 10~18 4 长径比L/d 20 70 24 9.92 57.14 5.6~11.5 5 扭曲比y 2~4 12 1.93 2.39~4.45 3 2 4.25~8.25 压力p/MPa 4.2 1.69 1.0 0.8 0.98~1.49 1~3.7 0.7~1 质量流速G/(kg·m−2·s−1) 8000 7845 5100~10000 3845~7013 4000~20000 5000~16000 1100~9900 临界平衡态含气率xcr −0.07~0.0106 −0.15 −0.183~−0.152 −0.279~−0.111 −0.34~−0.256 −0.473~−0.13 −0.31~−0.18 临界热流密度qcr/(MW·m−2) 10~15 13 18.24~35.78 9.90~32.32 19.8~45.9 16.8~68.6 11.6~51 数据点 4 1 5 52 15 47 15 L—管长 表 2 内插扭带管的高热流CHF经验关联式
Table 2. Empirical Correlation of High Heat Flow CHF in Twisted-Tape Tube
作者 关联式 应用范围 Drizius[23] ${q_{ {\text{cr, TT} } } } = \dfrac{G}{ { { {(2y)}^{0.1} } } }\left( {\dfrac{ {1.7 \times { {10}^5} } }{\xi } + \dfrac{ {17.3\xi } }{ { {4^{0.01\xi } } } } } \right), \xi=L / d_{\mathrm{h}}$ d=1.6 mm, p=0.4~1.4 MPa,
G=4000~25000 kg/(m²·s), y=1~5Schlosser[24] ${q_{ {\text{cr,TT} } } } = 0.23{f_{ {\text{TT} } } }\left[ {1 + 0.00216{ {\left( {\dfrac{ { {p } } }{ { {p_{ {\text{cr} } } } } } } \right)}^{1.8} }R{e^{0.5} }Ja} \right]G{h_{ {\text{fg} } } }\\ f = 8{\left( { { { {d } } \mathord{\left/ {\vphantom { { {d_{\text{h} } } } { {d_0} } } } \right. } { {d_0} } } } \right)^{0.32} }R{e^{ - 0.6} } ,Ja = \dfrac{ { {c_p}\Delta {T_{ {\text{sub} } } } } }{ { {h_{ {\text{fg} } } } } }\dfrac{ { {\rho _{\text{l} } } } }{ { {\rho _{\text{g} } } } }\\Re = \dfrac{ { {u_{\text{r} } }{d_{\text{h} } } } }{\mu },{u_{\text{r} } } = u{\left( {1 + \dfrac{ { { {\text{π} }^2} } }{ {4{y^2} } } } \right)^{0.5} } , p_{ {\rm{cr} } }=22.1 \;\mathrm{MPa}, d_0=12.7 \;\mathrm{mm}$ d=3~10 mm, p=6.9~13.8 MPa,
G=700~6000 kg/(m²·s)Koski[25] ${q_{ {\text{cr,TT} } } } = 0.23{f_{ {\text{TT} } } }\left[ {1 + 0.00216{ {\left( {\dfrac{p}{ { {p_{ {\text{cr} } } } } } } \right)}^{1.8} }R{e^{0.5} }Ja} \right]G{h_{ {\text{fg} } } }\\ f = 8{\left( {\dfrac{ { {d_{\text{h} } } }}{ { {d} } } } \right)^{0.32} }R{e^{ - 0.6} },Ja = \dfrac{ { {c_p}\Delta {T_{ {\text{sub} } } } } }{ { {H_{ {\text{fg} } } } } }\dfrac{ { {\rho _{\text{l} } } }}{ { {\rho _{\text{g} } } }} \\{ { {f_{ {\text{TT} } } }} \mathord{\left/ {\vphantom { { {f_{ {\text{TT} } } }} f} } \right. } f} = 2.2{y^{ - 0.406} },p_{ {\rm{cr} } }=22.1 \;\mathrm{MPa}, d_0=12.7 \;\mathrm{mm}$ d=3~10 mm, p=6.9~13.8 MPa,
G=700~6000 kg/(m²·s)Nariai-Inasaka[26] $\begin{gathered} {q_{ {\text{cr, TT} } } } = {q_{ {\text{cr, smooth} } } }{\left[ {1 + 0.01\theta \exp \left( { - {p^2} } \right)} \right]^{1/6} } \\ \theta = \dfrac{ { { {\text{π} }^2}u_{ {\text{ax} } }^2} }{ {2g{d_{\text{i} } }{y^2} } }{\text{; } }{u_{ {\text{ax} } } } = \dfrac{G}{ { {\rho _{\text{m} } } }};{\text{ } }{\rho _{\text{m} } } = {\left( {\dfrac{ {x'} }{ { {\rho _{\text{g} } } }} + \dfrac{ {1 - x'} }{ { {\rho _{\text{l} } } } } } \right)^{ - 1} } \\ \end{gathered}$ d=3.45~10.02 mm, p=0.1~3.8 MPa,
u=4.5~47.5 m/s, y=2.08~∞Arment[27] $ \begin{gathered} {q_{{\text{cr, TT}}}} = {q_{{\text{cr, smooth}}}}{\left[ {1 + 0.7\theta \exp \left( { - 0.09{{{\rho _{\text{l}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{l}}}} {{\rho _{\text{g}}}}}} \right. } {{\rho _{\text{g}}}}}} \right)} \right]^{0.14}} \\ {q_{{\text{cr, smooth}}}} = f\left( {p,G,x} \right){k_{\text{d}}}{k_{\text{L}}} \\ {k_{\text{d}}} = {\left( {{d \mathord{\left/ {\vphantom {d {8{\text{ mm}}}}} \right. } {8{\text{ mm}}}}} \right)^{ - 0.5}};{\text{ }}{k_{\text{L}}} = \exp ({d \mathord{\left/ {\vphantom {d L}} \right. } L}){\text{ (if }}{d \mathord{\left/ {\vphantom {d L}} \right. } L} \leqslant 0.2,{\text{ }}x \leqslant 0) \\ \end{gathered} $ G=678~7845 kg/(m²·s), d=4.4~11.51 mm,
p=0.8~14.7 MPa, y=1.93~445Yan[11] $ \begin{gathered} {q_{{\text{cr, TT}}}} = {q_{{\text{cr, smooth}}}}{\left[ {1 + 0.7\theta \exp \left( { - 0.09{{{\rho _{\text{l}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{l}}}} {{\rho _{\text{g}}}}}} \right. } {{\rho _{\text{g}}}}}} \right)} \right]^{0.14}} \\ {q_{{\text{cr, smooth}}}} = f\left( {p,G,x} \right){k_{\text{d}}} \\ {k_{\text{d}}} = {\left( {{d \mathord{\left/ {\vphantom {d {8{\text{ mm}}}}} \right. } {8{\text{ mm}}}}} \right)^{ - 0.5}} \\ \end{gathered} $ G=678~7845 kg/(m²·s), d=4.4~11.51 mm,
p=0.8~14.7 MPa, y=1.93~445qcr, TT—临界热流密度(内插扭带管);qcr, smooth—临界热流密度(光滑管);Ja—雅各布数;cp—定压比热容;Re—雷诺数;μ—动力粘度;ur—合成速度;pcr—临界压力;ρl—液相密度;ρg—汽相密度;ρm—平均流体密度;f—光滑管摩擦阻力系数;fTT—扭带管摩擦阻力系数;θ—离心力影响因子;uax—修正速度;kd—直径因素校正因子;kL—长度因素校正因子;u—流速;g—重力加速度;x′—真实干度 表 3 经验关联式CHF预测性能
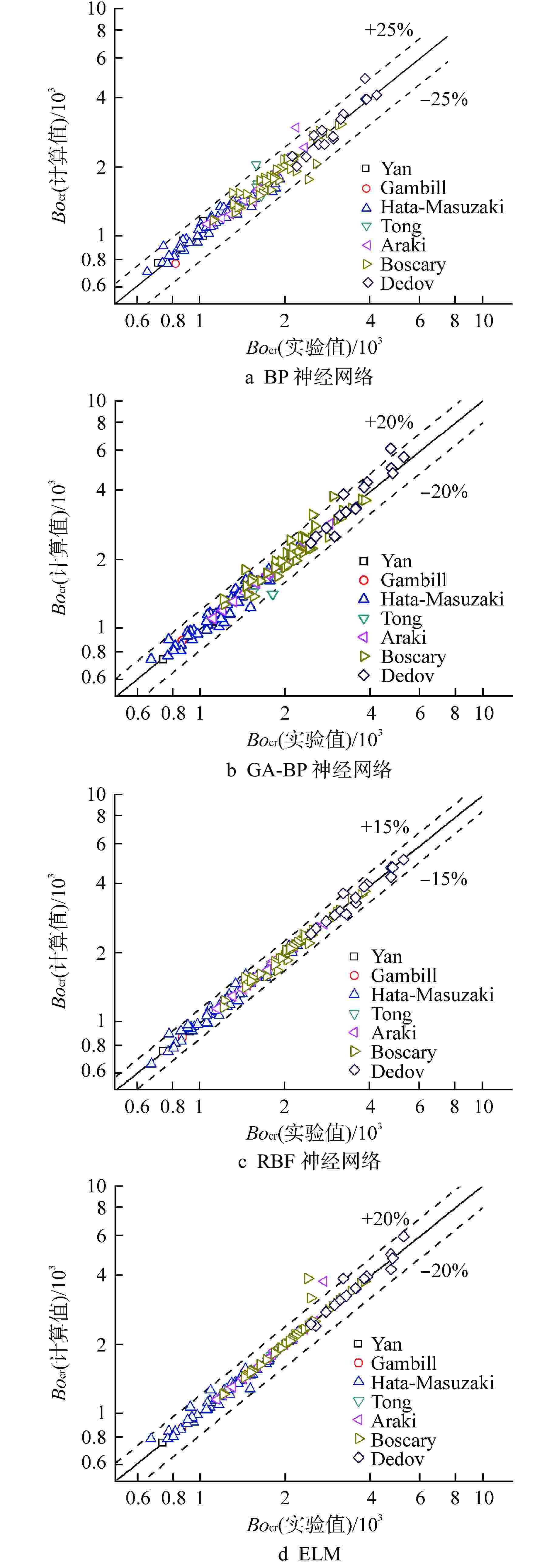
Table 3. Prediction Performance of Empirical Correlations for CHF
关联式 MAE/% RMSE/% Drizius 180.19 206.47 Tong 75-Ⅰ 74.013 105.02 Tong 75-Ⅱ 125.21 163.49 Nariai-Inasaka 226.07 303.42 Arment 17.66 21.25 Modified Arment 18.27 23.24 表 4 机器学习模型的预测性能
Table 4. Prediction Performance of Machine Learning Models
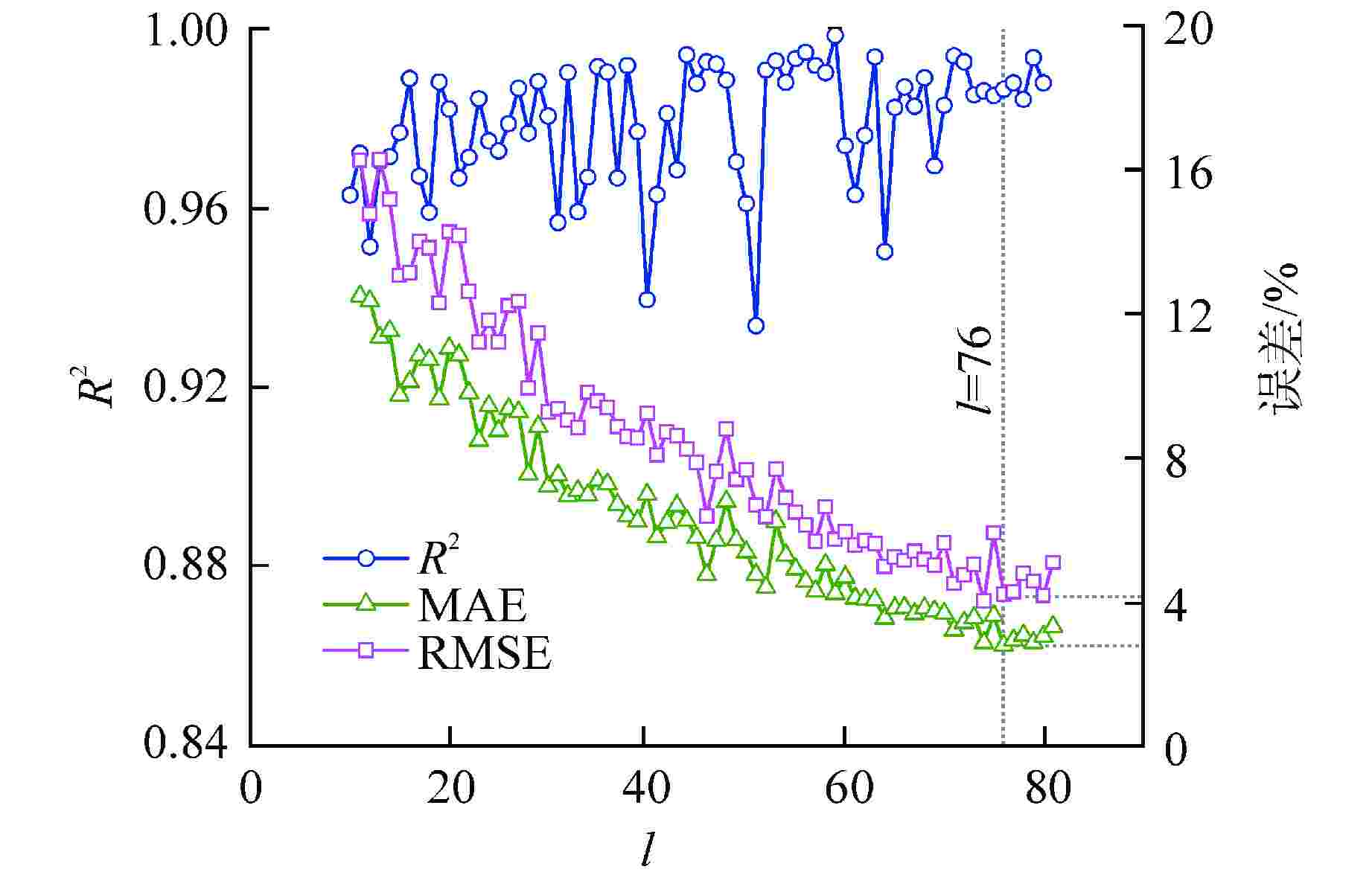
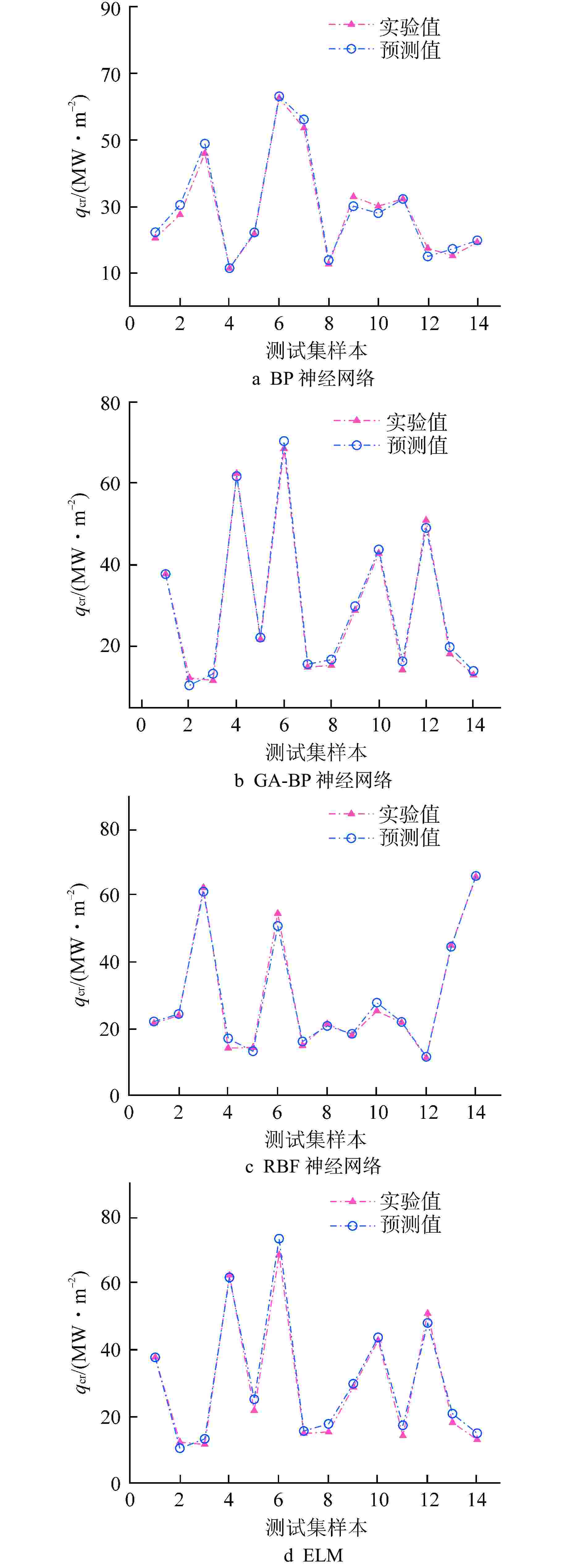
机器学习模型 MAE/% RMSE/% BP神经网络 6.66 9.23 GA-BP神经网络 5.89 8.21 RBF神经网络 2.75 7.89 ELM 2.79 4.22 -
[1] DOBRAN F. Fusion energy conversion in magnetically confined plasma reactors[J]. Progress in Nuclear Energy, 2012, 60: 89-116. doi: 10.1016/j.pnucene.2012.05.008 [2] FANG X D, YUAN Y L, XU A Y, et al. Review of correlations for subcooled flow boiling heat transfer and assessment of their applicability to water[J]. Fusion Engineering and Design, 2017, 122: 52-63. doi: 10.1016/j.fusengdes.2017.09.008 [3] 颜建国,郭鹏程,马嘉琦,等. 高热流条件下过冷沸腾流动阻力特性试验研究[J]. 化工学报,2019, 70(11): 4257-4267. [4] HATA K, SHIRAI Y, MASUZAKI S. Heat transfer and critical heat flux of subcooled water flow boiling in a HORIZONTAL circular tube[J]. Experimental Thermal and Fluid Science, 2013, 44: 844-857. doi: 10.1016/j.expthermflusci.2012.10.001 [5] YAN J G, BI Q C, CAI L Z, et al. Subcooled flow boiling heat transfer of water in circular tubes with twisted-tape inserts under high heat fluxes[J]. Experimental Thermal and Fluid Science, 2015, 68: 11-21. doi: 10.1016/j.expthermflusci.2015.04.003 [6] BOURNONVILLE Y, GRANDOTTO M, PASCAL-RIBOT S, et al. Numerical simulation of swirl-tube cooling concept, application to the ITER project[J]. Fusion Engineering and Design, 2009, 84(2-6): 501-504. doi: 10.1016/j.fusengdes.2008.11.028 [7] HATA K, MASUZAKI S. Subcooled boiling heat transfer for turbulent flow of water in a short vertical tube[J]. Journal of Heat Transfer, 2009, 132(1): 011501. [8] YAGOV V V. Heat transfer and crisis in swirl flow boiling[J]. Experimental Thermal and Fluid Science, 2005, 29(7): 871-883. doi: 10.1016/j.expthermflusci.2005.03.013 [9] DEDOV A V, KOMOV A T, VARAVA A N, et al. Hydrodynamics and heat transfer in swirl flow under conditions of one-side heating. Part 1: Pressure drop and single-phase heat transfer[J]. International Journal of Heat and Mass Transfer, 2010, 53(19-20): 4123-4131. doi: 10.1016/j.ijheatmasstransfer.2010.05.034 [10] DEDOV A V, KOMOV A T, VARAVA A N, et al. Hydrodynamics and heat transfer in swirl flow under conditions of one-side heating. Part 2: Boiling heat transfer. Critical heat fluxes[J]. International Journal of Heat and Mass Transfer, 2010, 53(21-22): 4966-4975. doi: 10.1016/j.ijheatmasstransfer.2010.05.035 [11] YAN J G, BI Q C, ZHU G, et al. Critical heat flux of highly subcooled water flow boiling in circular tubes with and without internal twisted tapes under high mass fluxes[J]. International Journal of Heat and Mass Transfer, 2016, 95: 606-619. doi: 10.1016/j.ijheatmasstransfer.2015.12.024 [12] 刘斌,袁博,赵建福,等. 微重力流动沸腾临界热流密度预测经验关联式[J]. 工程热物理学报,2020, 41(10): 2479-2483. [13] 钱虹,江诚,潘岳凯,等. 基于时间序列神经网络的蒸汽发生器传热管泄漏程度诊断研究[J]. 核动力工程,2020, 41(2): 160-167. doi: 10.13832/j.jnpe.2020.02.0160 [14] LIANG X, XIE Y Q, DAY R, et al. A data driven deep neural network model for predicting boiling heat transfer in helical coils under high gravity[J]. International Journal of Heat and Mass Transfer, 2021, 166: 120743. doi: 10.1016/j.ijheatmasstransfer.2020.120743 [15] PARK H M, LEE J H, KIM K D. Wall temperature prediction at critical heat flux using a machine learning model[J]. Annals of Nuclear Energy, 2020, 141: 107334. doi: 10.1016/j.anucene.2020.107334 [16] QIU Y, GARG D, KIM S M, et al. Machine learning algorithms to predict flow boiling pressure drop in mini/micro-channels based on universal consolidated data[J]. International Journal of Heat and Mass Transfer, 2021, 178: 121607. doi: 10.1016/j.ijheatmasstransfer.2021.121607 [17] 马栋梁,周涛,黄彦平. 基于机器学习的超临界水传热恶化判定研究[J]. 核动力工程,2021, 42(4): 91-95. doi: 10.13832/j.jnpe.2021.04.0091 [18] GAMBILL W R, BUNDY R D, WANSBROUGH R W. Heat transfer, burnout, and pressure drop for water in swirl flow through tubes with internal twisted tapes: ORNL-2911[R]. Oak Ridge, Tenn: Oak Ridge National Laboratory, 1960. [19] TONG W, BERGLES A E, JENSEN M K. Critical heat flux and pressure drop of subcooled flow boiling in small-diameter tubes with twisted-tape inserts[J]. Journal of Enhanced Heat Transfer, 1996, 3(2): 95-108. doi: 10.1615/JEnhHeatTransf.v3.i2.30 [20] HATA K, MASUZAKI S. Heat transfer and critical heat flux of subcooled water flow boiling in a SUS304-tube with twisted-tape insert[J]. Journal of Thermal Science and Engineering Applications, 2011, 3(1): 012001. doi: 10.1115/1.4003609 [21] ARAKI M, SATO K, SUZUKI S, et al. Critical-heat-flux experiment on the screw tube under one-sided-heating conditions[J]. Fusion Technology, 1996, 29(4): 519-528. doi: 10.13182/FST96-A30695 [22] BOSCARY J, FABRE J, SCHLOSSER J. Critical heat flux of water subcooled flow in one-side heated swirl tubes[J]. International Journal of Heat and Mass Transfer, 1999, 42(2): 287-301. doi: 10.1016/S0017-9310(98)00108-2 [23] DRIZIUS M R M, SKEMA R K, SLANCIAUSKAS A A. Boiling crisis in swirled flow of water in pipes[J]. Heat Transfer - Soviet Research, 1978, 10(4): 1-7. [24] SCHLOSSER J, CHAPPUIS P, DESCHAMPS P, et al. Thermal-hydraulic tests on net divertor targets using swirl tubes[Z]//Proceedings of the 1991 Winter Meeting of the American Nuclear Society. San Francisco: American Nuclear Society, 1991. [25] KOSKI J A. Thermal-hydraulic considerations in the surface contouring of a limited head for Tore Supra[Z]//Proceedings of the 7th Proc Nuclear Thermal Hydraulics, ANS Winter Meeting. 1991. [26] NARIAI H, INASAKA F, FUJISAKI W, et al. Critical heat flux of subcooled flow boiling in tubes with internal twisted tape[Z]//Proceedings of the 7th Proc, Nuclear Thermal Hydraulics, ANS Winter Meeting. 1991. [27] ARMENT T W, TODREAS N E, BERGLES A E. Critical heat flux and pressure drop for tubes containing multiple short-length twisted-tape swirl promoters[J]. Nuclear Engineering and Design, 2013, 257: 1-11. doi: 10.1016/j.nucengdes.2012.12.008 [28] 颜建国,郑书闽,郭鹏程,等. 基于GA-BP神经网络的超临界CO2传热特性预测研究[J]. 化工学报,2021, 72(9): 4649-4657. [29] 关鹏,焦玉勇,段新胜. 基于RBF神经网络的土体导热系数非线性预测[J]. 太阳能学报,2021, 42(3): 171-178. doi: 10.19912/j.0254-0096.tynxb.2018-1118 [30] 崔江,唐军祥,张卓然,等. 基于极限学习机的航空发电机旋转整流器快速故障分类方法研究[J]. 中国电机工程学报,2018, 38(8): 2458-2466. doi: 10.13334/J.0258-8013.PCSEE.162334 [31] TONG L S. A phenomenological study of critical heat flux: ASME Paper 75-1-HT-68[R]. New York, USA: ASME, 1975. -





 下载:
下载: