基于逐步回归无量纲棒束CHF关系式开发与DNBR限值确定

殷园; 冯思敏; 庞波; 席炎炎; 张玉相; 傅先刚

doi:10.13832/j.jnpe.2023.04.0072

基于逐步回归无量纲棒束CHF关系式开发与DNBR限值确定

doi: 10.13832/j.jnpe.2023.04.0072

殷园^{1, 2,},
冯思敏^{1, 2},
庞波^{1, 2, ,},
席炎炎³,
张玉相³,
傅先刚³

1.
深圳大学核科学与技术系，广东深圳，518060
2.
国家能源核电运营及寿命管理技术研发中心-核电运营安全技术联合实验室，广东深圳，518060
3.
中广核研究院有限公司，广东深圳，518116

基金项目: 深圳市高等院校稳定支持计划面上项目（20200803132736020）

详细信息

作者简介:
殷　园（1964—），女，特聘研究员，现主要从事先进核能系统方面的研究，E-mail: yinyuan@szu.edu.cn

通讯作者:
庞　波，E-mail: bo.pang@szu.edu.cn

中图分类号: TL334
计量
- 文章访问数: 1023
- HTML全文浏览量: 64
- PDF下载量: 41
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-19
- 修回日期: 2022-09-02
- 刊出日期: 2023-08-15

Development of Dimensionless Rod-bundle CHF Correlation Based on Stepwise Regression and Determination of DNBR Limit

Yin Yuan^{1, 2
,},
Feng Simin^{1, 2},
Pang Bo^{1, 2
, ,},
Xi Yanyan³,
Zhang Yuxiang³,
Fu Xiangang³

1.
Department of Nuclear Science and Technology, Shenzhen University (SZU), Shenzhen, Guangdong, 518060, China
2.
Institute of Nuclear Power Operation Safety Technology (INPOST), Affiliated to the National Energy R & D Center on Nuclear Power Operation and Life Management, Shenzhen, Guangdong, 518060, China
3.
China Nuclear Power Technology Research Institute Co., Ltd., Shenzhen, Guangdong, 518116, China

摘要

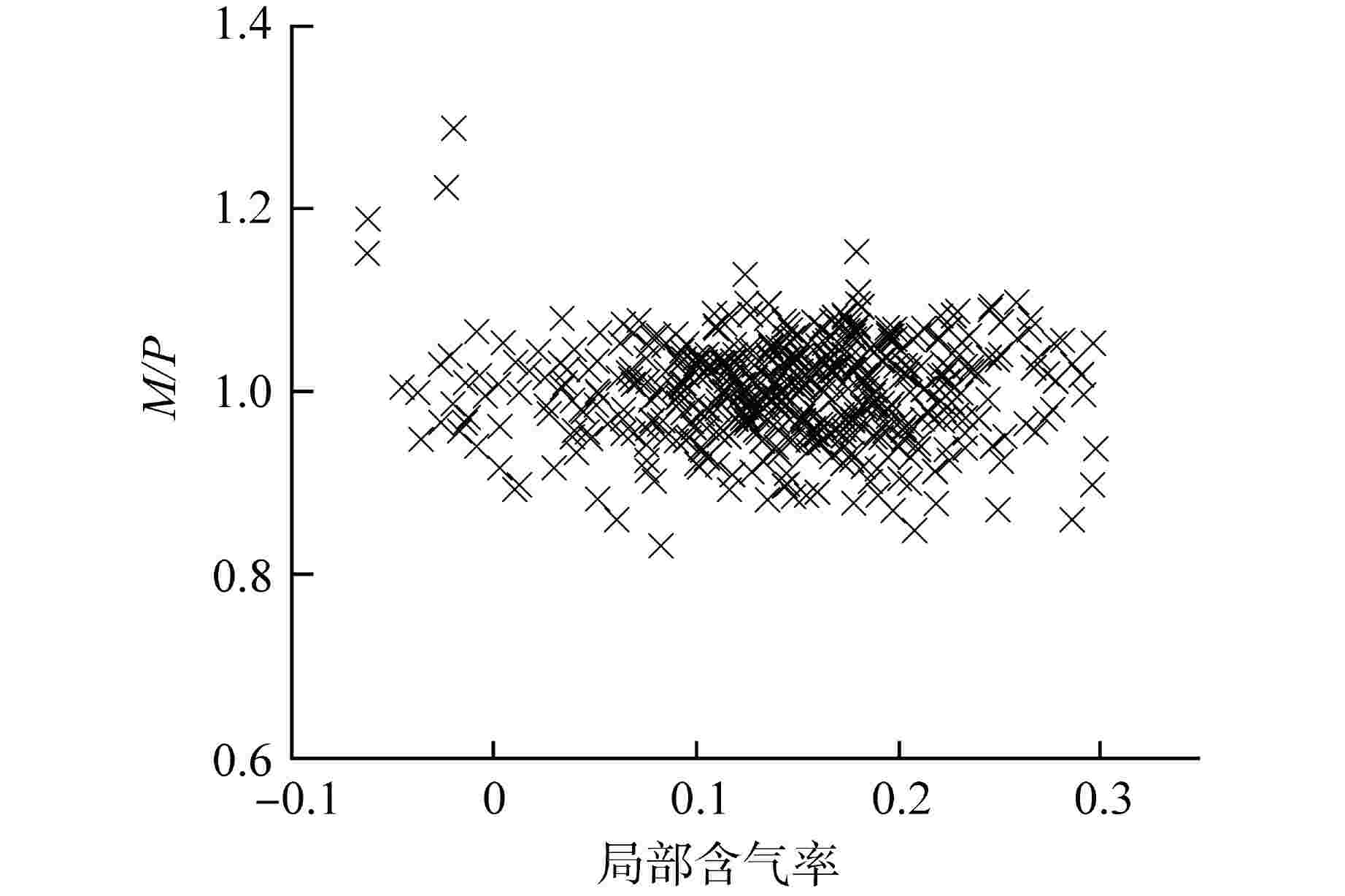
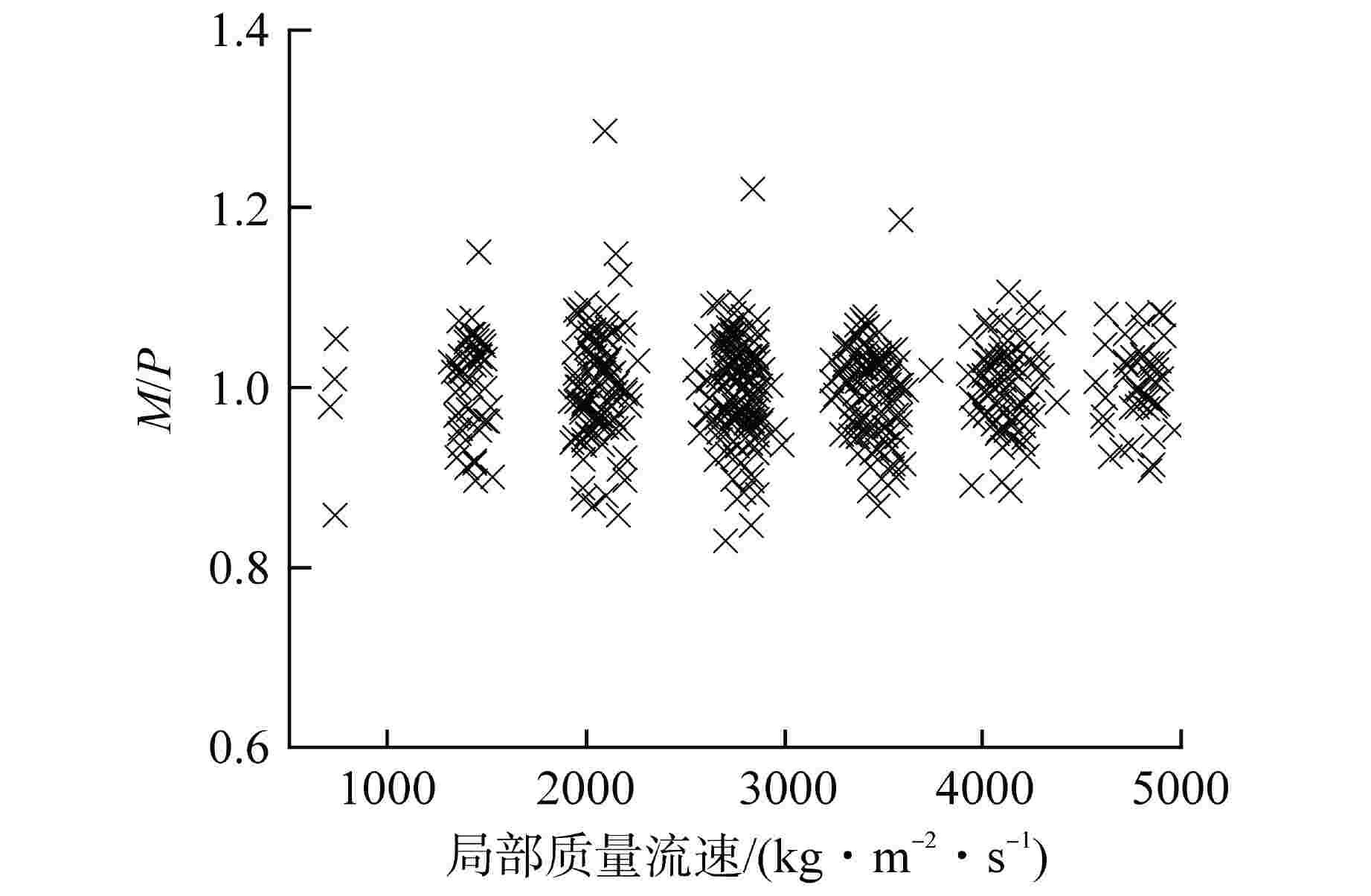
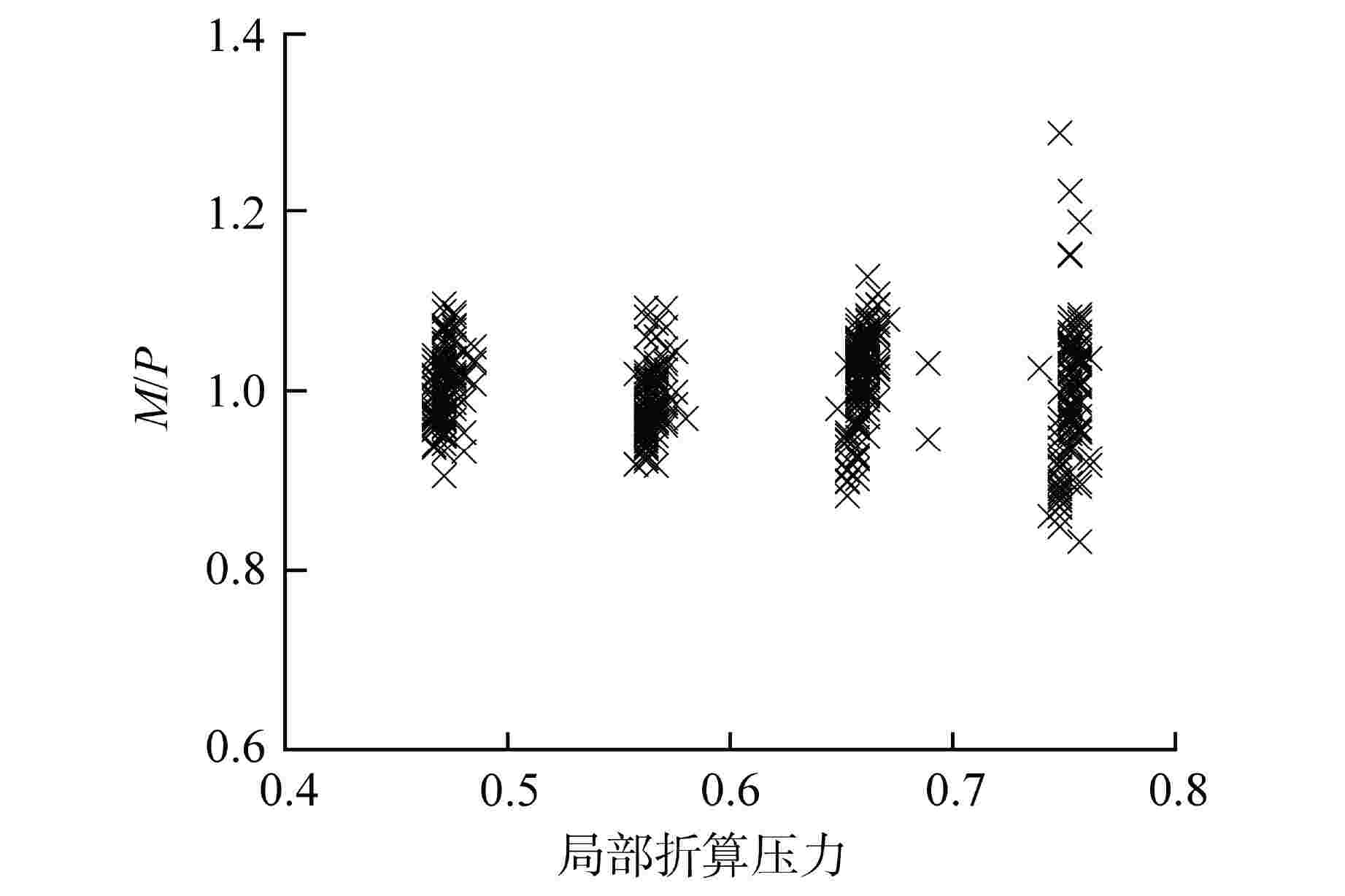
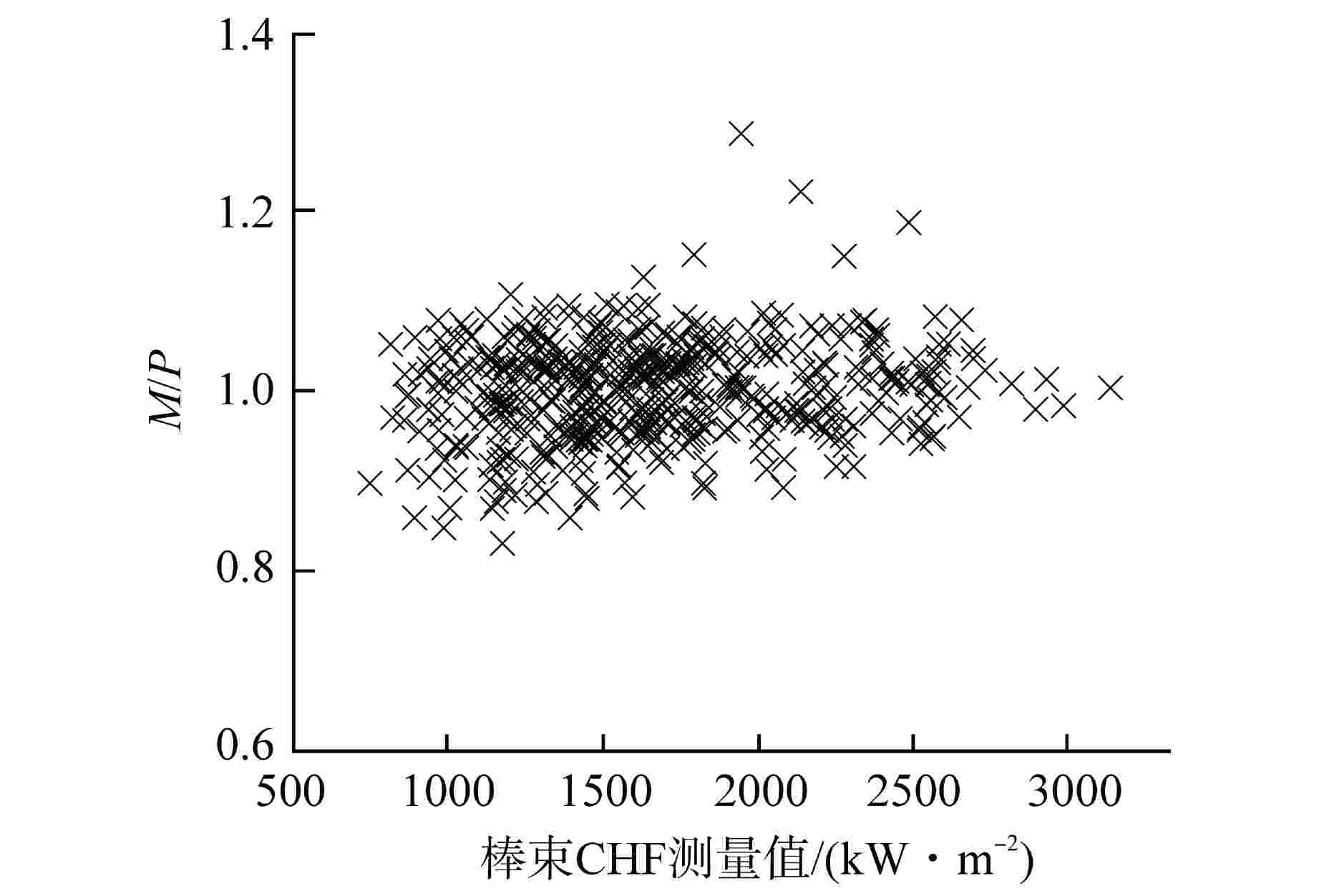
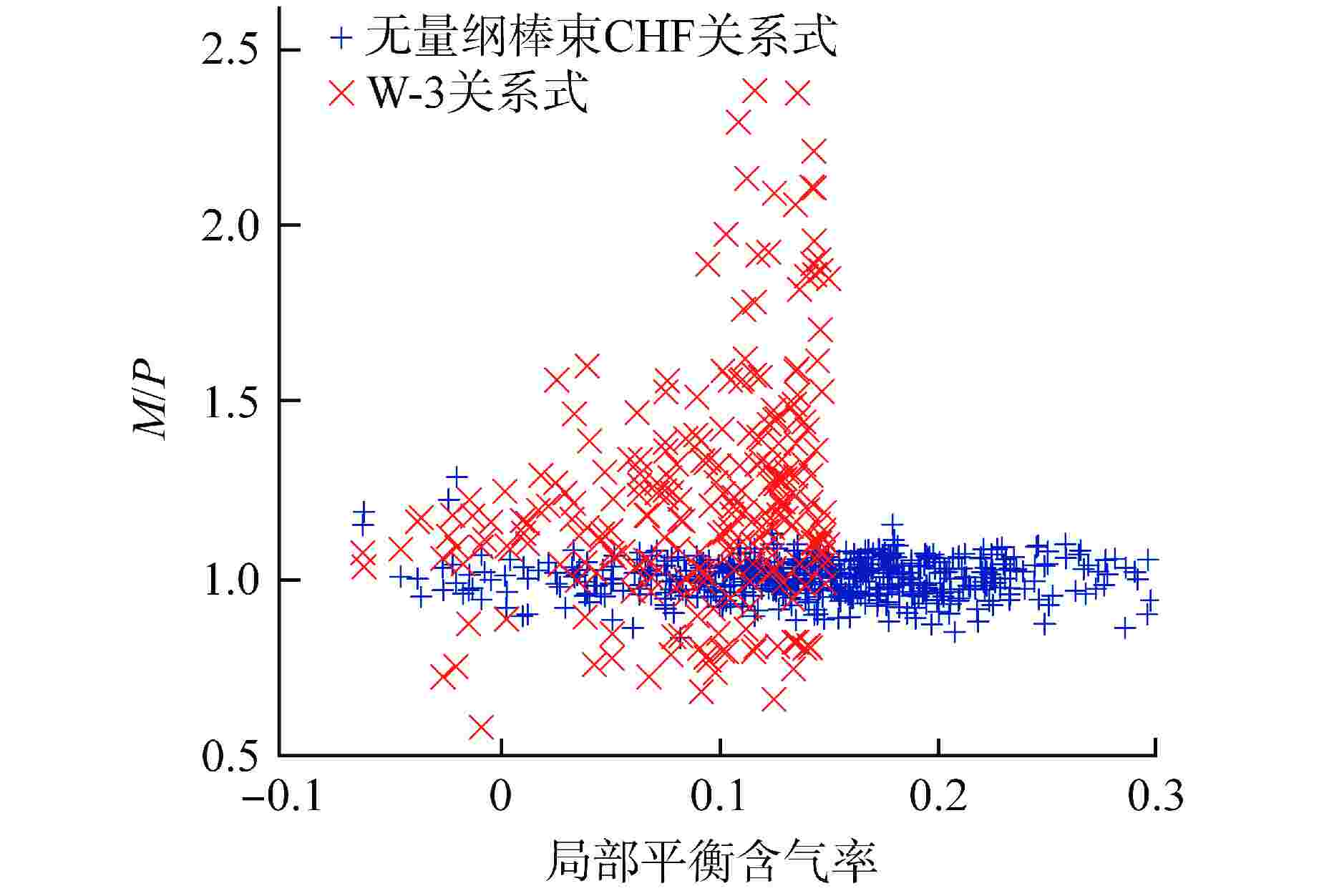
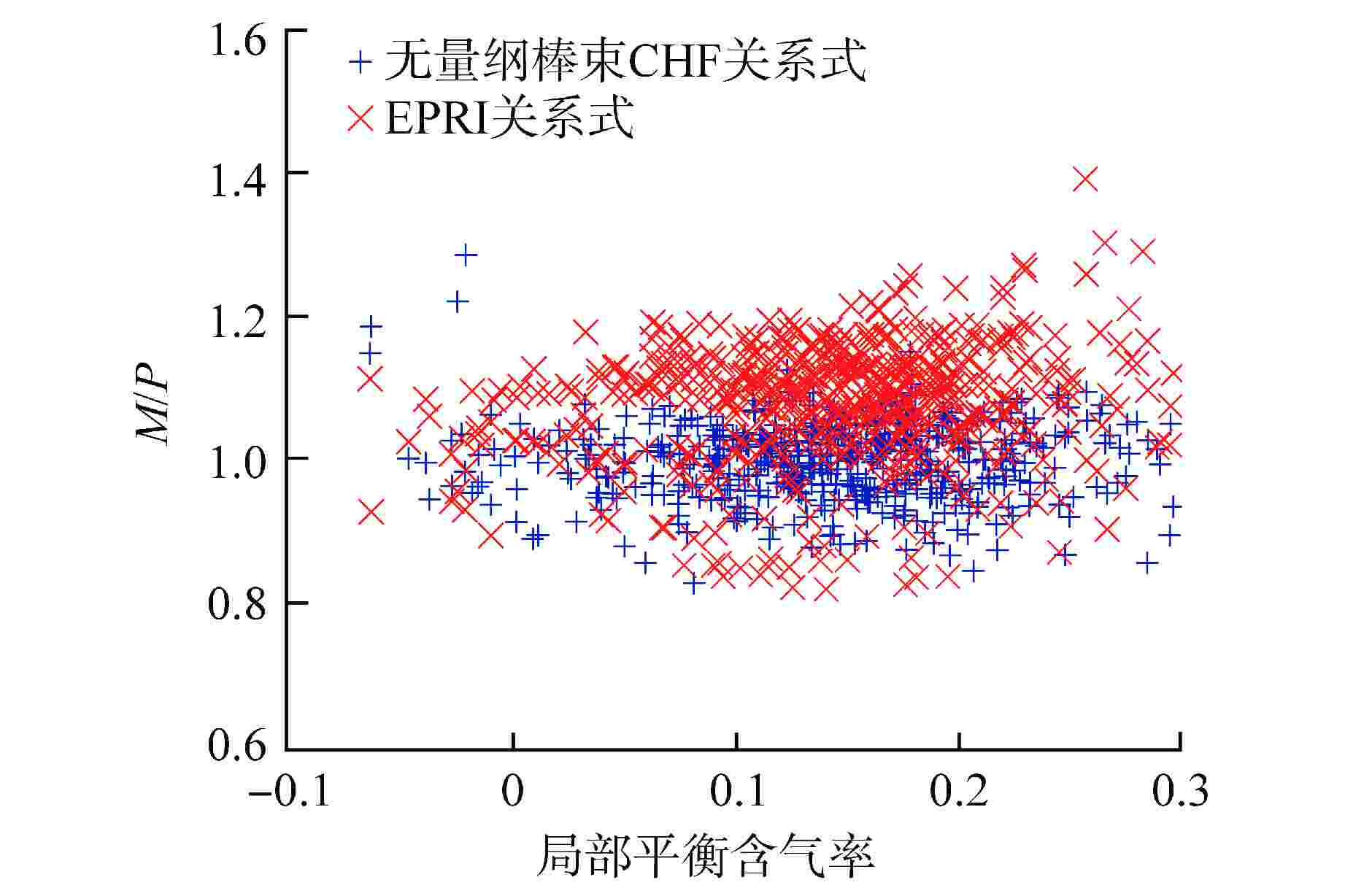
摘要: 针对目前国内外先进压水堆棒束临界热流密度（CHF）经验关系式普遍存在数学形式复杂、自变量系数众多且缺乏物理意义的共性问题，以美国电力研究院（EPRI）棒束CHF数据库中遴选的485个5×5压水堆棒束CHF数据点为基础，基于逐步回归分析开发了一套新型无量纲棒束CHF关系式。考虑了导向管冷壁效应与轴向非均匀加热效应后，实测CHF与预测CHF之比M/P的平均值为0.998，均方根偏差为0.0546，标准差为0.0546，基于分组法确定了关系式的95/95 偏离泡核沸腾比（DNBR）限值为1.16。
- 逐步回归分析 /
- 棒束临界热流密度（CHF） /
- 无量纲关系式 /
- 偏离泡核沸腾比（DNBR）
Abstract: At present, the empirical correlations of critical heat flux (CHF) of advanced PWR rod-bundles at home and abroad generally have the common problems of complex mathematical form, numerous independent variable coefficients and lack of physical significance. In this study, based on 485 rod-bundle CHF data points of 5×5 PWR rod-bundles selected from the rod bundle CHF database of American Electric Power Research Institute (EPRI), a new dimensionless CHF correlation is developed with stepwise regression analysis. Considering the cold wall effect and axial non-uniform heating effect of the guide tube, the average value of the ratio M/P between the measured CHF and the predicted CHF is 0.998, the root mean square error is 0.0546, and the standard deviation is 0.0546. Based on the grouping method, the limit of the 95/95 departure from nucleate boiling ratio (DNBR) of the correlation is determined to be 1.16.
- Stepwise regression /
- Rod-bundle CHF /
- Dimensionless correlation /
- DNBR

HTML全文

图 1 5×5棒束轴向示意图

Figure 1. Axial View of the 5×5 Test Rod-bundle

下载: 全尺寸图片幻灯片

图 2 5×5棒束截面示意图

Figure 2. Cross-sectional View of the 5×5 Test Rod Bundle

下载: 全尺寸图片幻灯片

图 3 M/P随局部平衡含气率的变化趋势

Figure 3. M/P Distribution versus Local Equilibrium Quality

下载: 全尺寸图片幻灯片

图 4 M/P随局部质量流速的变化趋势

Figure 4. M/P Distribution versus Local Mass Velocity

下载: 全尺寸图片幻灯片

图 5 M/P随局部折算压力的变化趋势

Figure 5. M/P Distribution versus Local Reduced Pressure

下载: 全尺寸图片幻灯片

图 6 M/P随棒束CHF测量值的变化趋势

Figure 6. M/P Distribution versus Measured CHF

下载: 全尺寸图片幻灯片

图 7 无量纲棒束CHF关系式与W-3关系式的对比

Figure 7. Comparison between the Dimensionless Rod-Bundle CHF Correlation with the W-3 Correlation

下载: 全尺寸图片幻灯片

图 8 无量纲棒束CHF关系式与EPRI关系式的对比

Figure 8. Comparison between the Dimensionless Rod-bundle CHF Correlation with the EPRI Correlation

下载: 全尺寸图片幻灯片

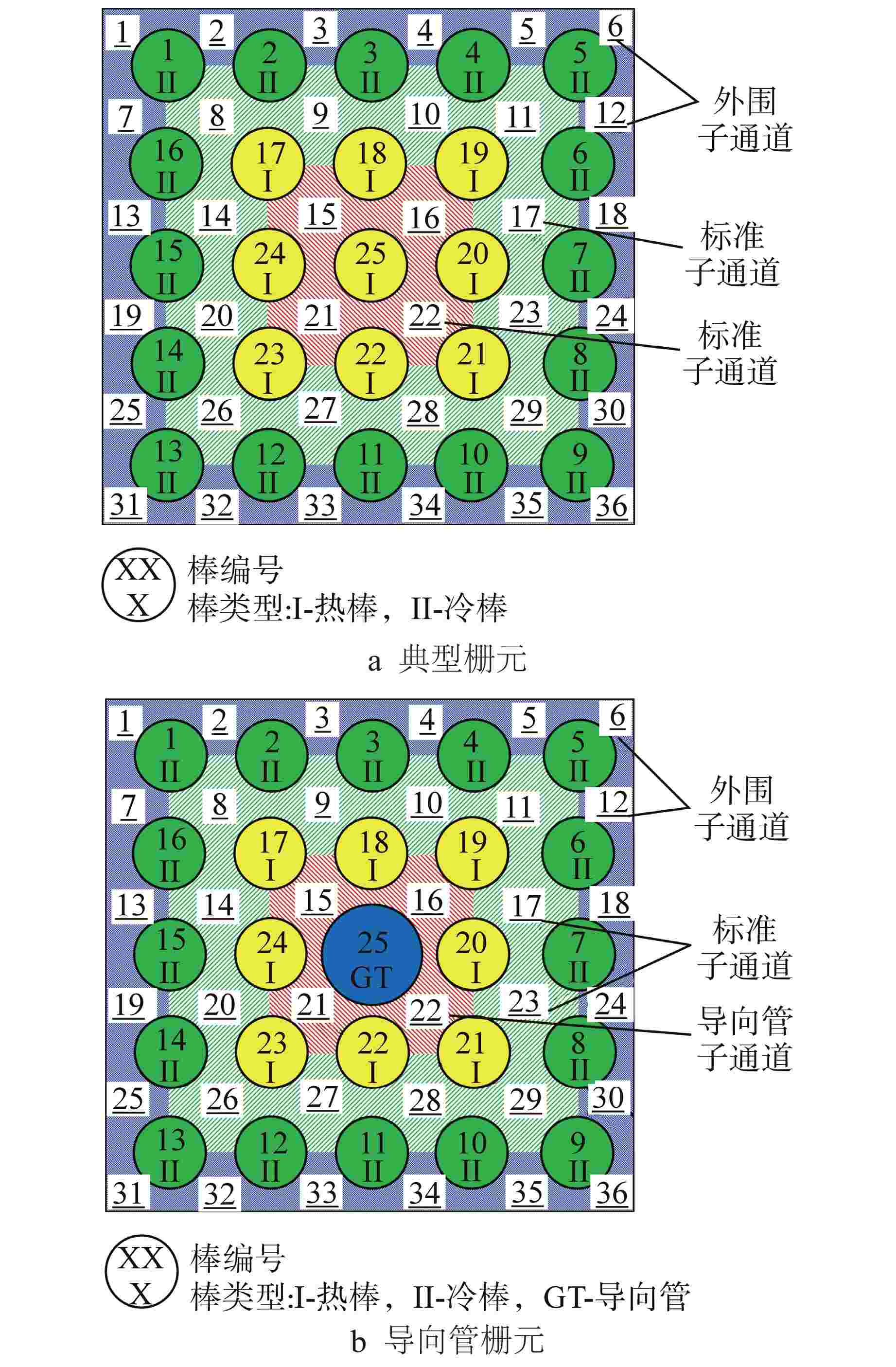
表 1 5×5棒束试验序列信息

Table 1. Specification of 5×5 Test Bundles

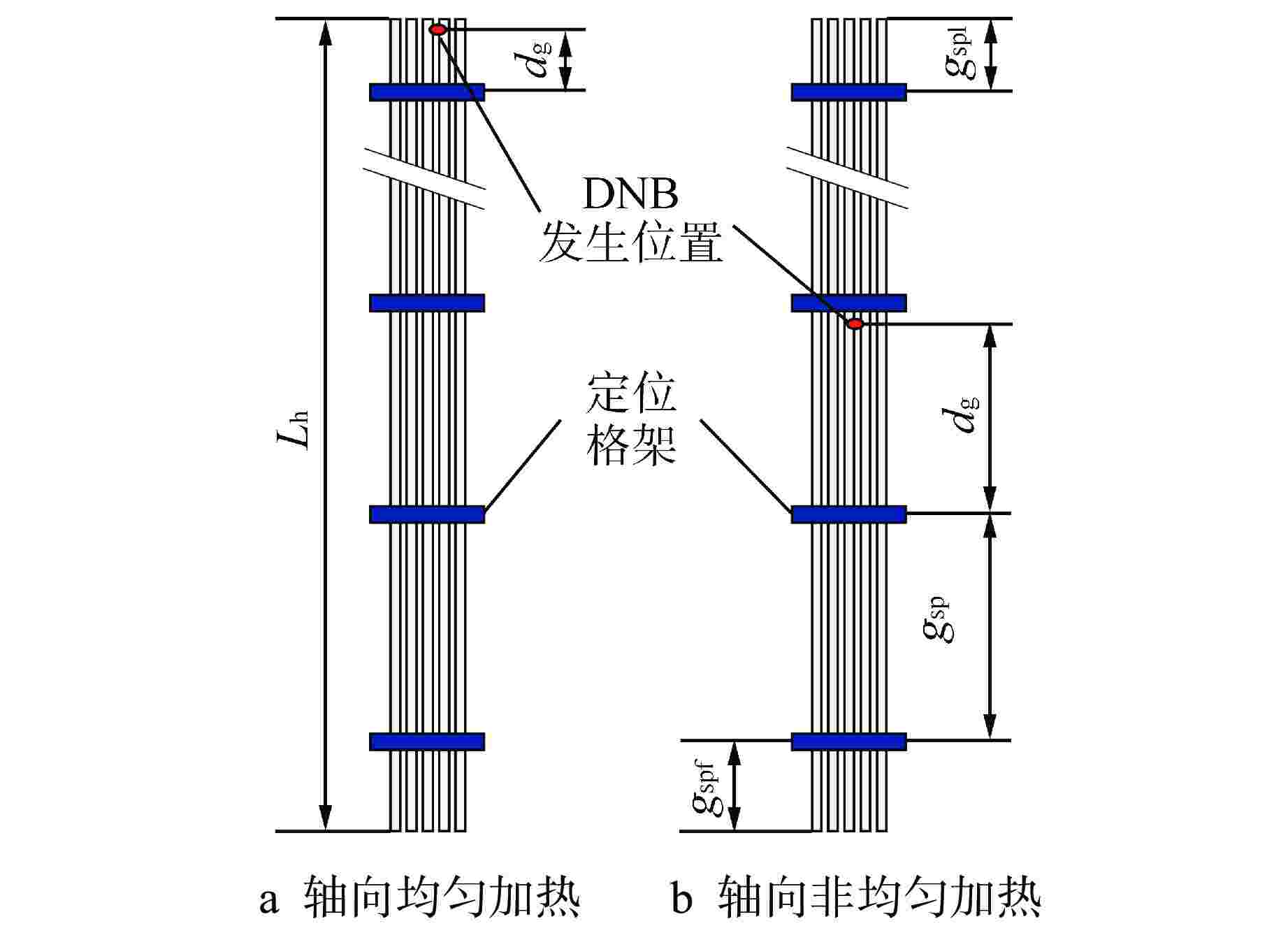
试验序列	L_h/mm	D_g/mm	d_g/mm	g_sp/mm	N
HTRF-156	4267.20		317.5	330.2	102
HTRF-157	2438.40		317.5	330.2	77
HTRF-160	2438.40		241.6	279.4	67
HTRF-161	4267.20		241.3	279.4	59
HTRF-163	2438.40		241.3	558.8	41
HTRF-158	2438.40	12.24	317.5	330.2	65
HTRF-164	4267.20		254.0	279.4	75
N—每个试验序列测试点数量

下载: 导出CSV

表 2 5×5棒束试验序列局部数据参数范围

Table 2. Local Data Range of 5×5 Test Bundles

试验序列	压力/ MPa	质量流速/ (kg·m⁻²·s⁻¹)	平衡含气率
轴向均匀加热典型栅元	10.3~16.7	710~5000	−0.06~0.30
轴向均匀加热导向管栅元	10.4~16.8	1300~4600	−0.05~0.29
轴向非均匀加热典型栅元	10.4~16.8	1300~4800	0.08~0.29

下载: 导出CSV

表 3 COBRA-IV-I子通道分析闭合条件

Table 3. Closure Models of Subchannel Analysis with COBRA-IV-I

子通道分析闭合模型		模型公式与参数
压降模型	单相湍流摩擦系数	$0.184R{e^{ - 0.2}}$
	两相摩擦倍增因子	Armand模型^[7]
	定位格架局部压降系数	0.570、1.250
含气率-空泡份额关系	过冷沸腾	Levy模型^[7]
含气率-空泡份额关系	饱和沸腾	修正Armand模型^[7]
子通道横向搅混模型	横流阻力系数	0.5
子通道横向搅混模型	湍流交混系数	0.02

下载: 导出CSV

表 4 无量纲关系式M/P数据误差参数

Table 4. Error Statistics of the Proposed Dimensionless Rod-Bundle CHF Correlation

试验序列	$ N $	$\bar \mu $	RMSE	s
HTRF-156	102	0.986	0.0526	0.0524
HTRF-157	77	1.006	0.0508	0.0504
HTRF-160	67	1.008	0.0639	0.0634
HTRF-161	59	0.978	0.0586	0.0581
HTRF-163	41	1.009	0.0437	0.0432
HTRF-158	65	1.005	0.0523	0.0519
HTRF-164	75	1.002	0.0507	0.0504
所有数据	485	0.998	0.0546	0.0546

下载: 导出CSV

表 5 M/P数据分组及关系式DNBR限值的确定

Table 5. Grouping of the M/P Data and Determination of the DNBR Limit

分组	试验序列	N	$\bar \mu $	s	正态分布	95/95 DNBR
1	HTRF-156、161	161	0.983	0.0549	否	1.156
2	HFRT-164	75	1.002	0.0504	是	1.110
3	HTRF-157、158、160、163	249	1.007	0.0537	否	1.119

下载: 导出CSV

参考文献(17)

[1]	CHENG X, MÜLLER U. Review on critical heat flux in water cooled reactors: FZKA-6825[R]. Karlsruhe: Forschungszentrum Karlsruhe, 2003.
[2]	张玉相,席炎炎,庞铮铮,等. CHF关系式开发与DNBR限值确定方法研究[J]. 核动力工程,2016, 37(5): 130-134.
[3]	TONG L S, WEISMAN J. Thermal analysis of pressurized water reactors[M]. 3rd ed. La Grange Park: American Nuclear Society, 1996: 478-490.
[4]	REDDY D G, FIGHETTI C F. Parametric study of CHF data Volume 2. A generalized subchannel CHF correlation for PWR and BWR fuel assemblies. Final report: EPRI-NP-2609-Vol. 2[R]. New York: Columbia University, 1983.
[5]	刘伟. 压水堆燃料组件临界热流密度关系式的开发、评估及应用[D]. 西安: 西安交通大学, 2013.
[6]	FIGHETTI C F, REDDY D G. Parametric study of CHF data. Volume 3, Part 1. Critical heat flux data. Final report: EPRI-NP-2609-Vol. 3-Pt. 1[R]. New York: Columbia University, 1982.
[7]	STEWART C W, WHEELER C L, CENA R J, et al. COBRA-IV: the model and the method: BNWL-2214[R]. Richland: Pacific Northwest Laboratories, 1977.
[8]	DRAPER N R, SMITH H. Applied regression analysis[M]. New York: John Wiley & Sons Inc, 1981.
[9]	WEISMAN J, PEI B S. Prediction of critical heat flux in flow boiling at low qualities[J]. International Journal of Heat and Mass Transfer, 1983, 26(10): 1463-1477. doi: 10.1016/S0017-9310(83)80047-7
[10]	LEE C H, MUDAWWAR I. A mechanistic critical heat flux model for subcooled flow boiling based on local bulk flow conditions[J]. International Journal of Multiphase Flow, 1988, 14(6): 711-728. doi: 10.1016/0301-9322(88)90070-5
[11]	TONG L S, TANG Y S. Boiling heat transfer and two-phase flow[M]. 2nd ed. Washington: Taylor & Francis Ltd. , 1997: 333.
[12]	GROENEVELD D C, CHENG S C, DOAN T. 1986 AECL-UO critical heat flux lookup table[J]. Heat Transfer Engineering, 1986, 7(1-2): 46-62. doi: 10.1080/01457638608939644
[13]	ROSAL E R, CERMAK J O, TONG L S, et al. High pressure rod bundle DNB data with axially non-uniform heat flux[J]. Nuclear Engineering and Design, 1974, 31(1): 1-20. doi: 10.1016/0029-5493(74)90129-0
[14]	刘伟, 杜思佳, 张渝, 等. 一种基于分组法的CHF关系式DNBR限值统计学确定方法: 中国, 201910887222.2[P]. 2020-01-24.
[15]	国家质量技术监督局. 数据的统计处理和解释正态性检验: GB/T 4882-2001[S]. 北京: 中国标准出版社, 2004:14-17.
[16]	OWEN D B. Factors for one-sided tolerance limits and for variables sampling plans: NSA-17-023849[R]. Albuquerque: Sandia Corporation, 1963.
[17]	NATRELLA M G. Experimental statistics[M]. Washington: NBS Handbook 91 National Bureau Standards, 1963: 31.