全堆芯热工子通道模型的JFNK全局求解方法研究

章运山; 周夏峰

doi:10.13832/j.jnpe.2023.05.0039

全堆芯热工子通道模型的JFNK全局求解方法研究

doi: 10.13832/j.jnpe.2023.05.0039

章运山,
周夏峰^,

华中科技大学，武汉，430074

基金项目: 国家自然科学基金（12005073）；国防科技工业核动力技术创新中心项目（HDLCXZX-2021-HD-033）

详细信息

作者简介:
章运山（1998—），男，硕士研究生，现主要从事核反应堆堆芯子通道模型研究，E-mail: zhangyunshan_dj@foxmail.com

通讯作者:
周夏峰，E-mail: zhouxiafeng@hust.edu.cn

中图分类号: TL339
计量
- 文章访问数: 1810
- HTML全文浏览量: 278
- PDF下载量: 392
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-14
- 修回日期: 2022-12-23
- 刊出日期: 2023-10-13

Study on JFNK Global Solution Method of of Full-core Thermal Sub-channel Model

Zhang Yunshan,
Zhou Xiafeng^,

Huazhong University of Science and Technology, Wuhan, 430074, China

摘要

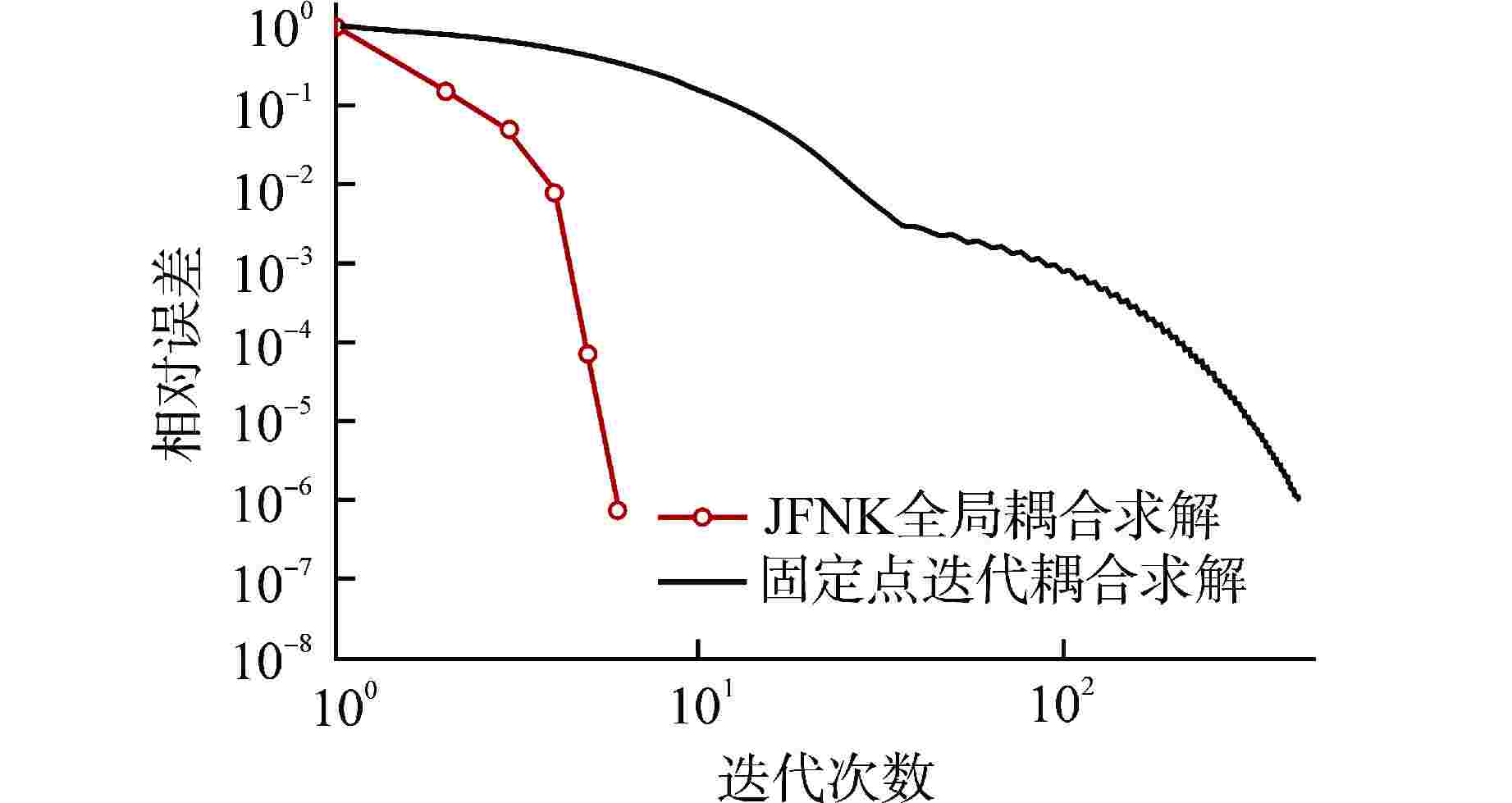
摘要: 反应堆热工子通道模型详细考虑了轴向流动、横向交混，湍流交混等多种耦合因素，是堆芯热工水力分析的关键模型，但是这些因素为子通道数值模拟带来了困难和挑战。为了提高热工子通道模型的计算效率和收敛性，本文基于Jacobian-Free Newton-Krylov（JFNK）全局求解方法（以下简称JFNK方法），开发了全堆芯热工子通道模型的全局求解框架，并基于现有程序的模型和框架建立了基于物理预处理的残差系统，增强JFNK方法的收敛速率。结果表明，JFNK方法的计算效率是固定点迭代方法的5倍，且JFNK方法的效率优势随着收敛精度的提高会更加明显。因此，对于复杂热工子通道模型，JFNK方法有着不错的潜力和效率优势。
- 全堆芯热工水力 /
- 子通道分析 /
- JFNK /
- 物理预处理
Abstract: The thermal sub-channel model of reactor takes into account many coupling factors such as axial flow, lateral mixing and turbulent mixing in detail, and it is the key model of thermal hydraulic analysis of the core. However, these factors bring difficulties and challenges to the numerical simulation of sub-channel. In order to improve the computational efficiency and convergence of the thermal sub-channel model, this paper develops a global solution framework for the thermal sub-channel model of the whole core based on the Jacobian-Free Newton-Krylov (JFNK) global solution method (hereinafter referred to as JFNK method), and establishes a residual system based on physical pretreatment according to the existing code model and framework to enhance the convergence rate of JFNK method. Numerical solutions show that the speedup of JFNK methods is about five compared with the fixed-point iterative method used in the original sub-channel models and there are higher efficiency for JFNK methods as convergence precision improves, which indicates the potential and efficiency advantages of JFNK methods for complicated thermal sub-channel model.
- Full-core thermal hydraulics /
- Sub-channel analysis /
- JFNK /
- Physical precondition

HTML全文

图 1 子通道流动及交错网格

∆P—轴向压降；∆Z—轴向间隔；j—轴向控制体j

Figure 1. Subchannel Flow and Staggered Mesh

下载: 全尺寸图片幻灯片

图 2 固定点迭代流程图

Figure 2. Flow Chart of Fixed-point Iteration

下载: 全尺寸图片幻灯片

图 3 JFNK方法流程图

Figure 3. Flow Chart of JFNK Method

下载: 全尺寸图片幻灯片

图 4 全堆芯组件编号及径向功率分布

Figure 4. Assembl Number and Radial Power Distribution of Full Core

下载: 全尺寸图片幻灯片

图 5 2×2径向网格

Figure 5. 2×2 Meshes in Radial Direction

下载: 全尺寸图片幻灯片

图 6 堆芯出口混合焓和质量流速

Figure 6. Mixing Enthalpy and Mass Flux at Core Outlet

下载: 全尺寸图片幻灯片

图 7 组件79和52对应通道轴向质量流速比较

Figure 7. Comparison of Axial Mass Fluxes in Assemblies 79 and 52

下载: 全尺寸图片幻灯片

图 8 组件79和52对应通道轴向混合焓比较

Figure 8. Comparison of Axial Mixing Enthalpies in Assemblies 79 and 52

下载: 全尺寸图片幻灯片

图 9 组件79和52对应通道轴向压力比较

Figure 9. Comparison of Axial Pressures in Assemblies 79 and 52　　　　　

下载: 全尺寸图片幻灯片

图 10 2种方法的收敛曲线

Figure 10. Convergence Curves of Two Methods

下载: 全尺寸图片幻灯片

图 11 不同松弛因子下固定点迭代收敛曲线

Figure 11. Convergence Curves of Fixed Point Iteration with Different Relaxation Factors

下载: 全尺寸图片幻灯片

表 1 全堆芯计算参数^[19-20]

Table 1. Calculation Parameters of Full Core

参数	量值
燃料组件数目	157
燃料组件边长/cm	21.504
燃料棒数目（每个燃料组件）	264
导向管和控制棒数目（每个燃料组件）	25
燃料棒外直径/cm	0.95
导向管外径/cm	1.245
棒中心间距/cm	1.26
参考热流密度/(W·cm⁻²)	55.6534
堆芯入口流量/(m³·h⁻¹)	64066.2
冷却剂入口温度/℃	292.4
堆芯出口压力/10⁵Pa	155
轴向功率因子峰值	1.55
轴向加热区起始点高度/cm	15.25
轴向加热区长度/cm	366.0

下载: 导出CSV

表 2 不同收敛精度对应的2种方法的收敛性比较

Table 2. Comparison of Convergence of Two Methods with Different Convergence Accuracies

收敛精度	固定点迭代方法		JFNK全局求解方法		加速比
收敛精度	时间/s	迭代次数	时间/s	Newton迭代次数	加速比
1×10⁻³	45.0	95	16.97	4	2.65
1×10⁻⁴	89.8	213	24.92	4	3.60
1×10⁻⁵	153.4	336	34.91	5	4.39
1×10⁻⁶	194.5	454	39.10	5	4.97

下载: 导出CSV

表 3 不同松弛因子下的2种方法的迭代次数和计算时间

Table 3. Iterative Number and Computation Time of Two Methods with Different Relaxation Factors

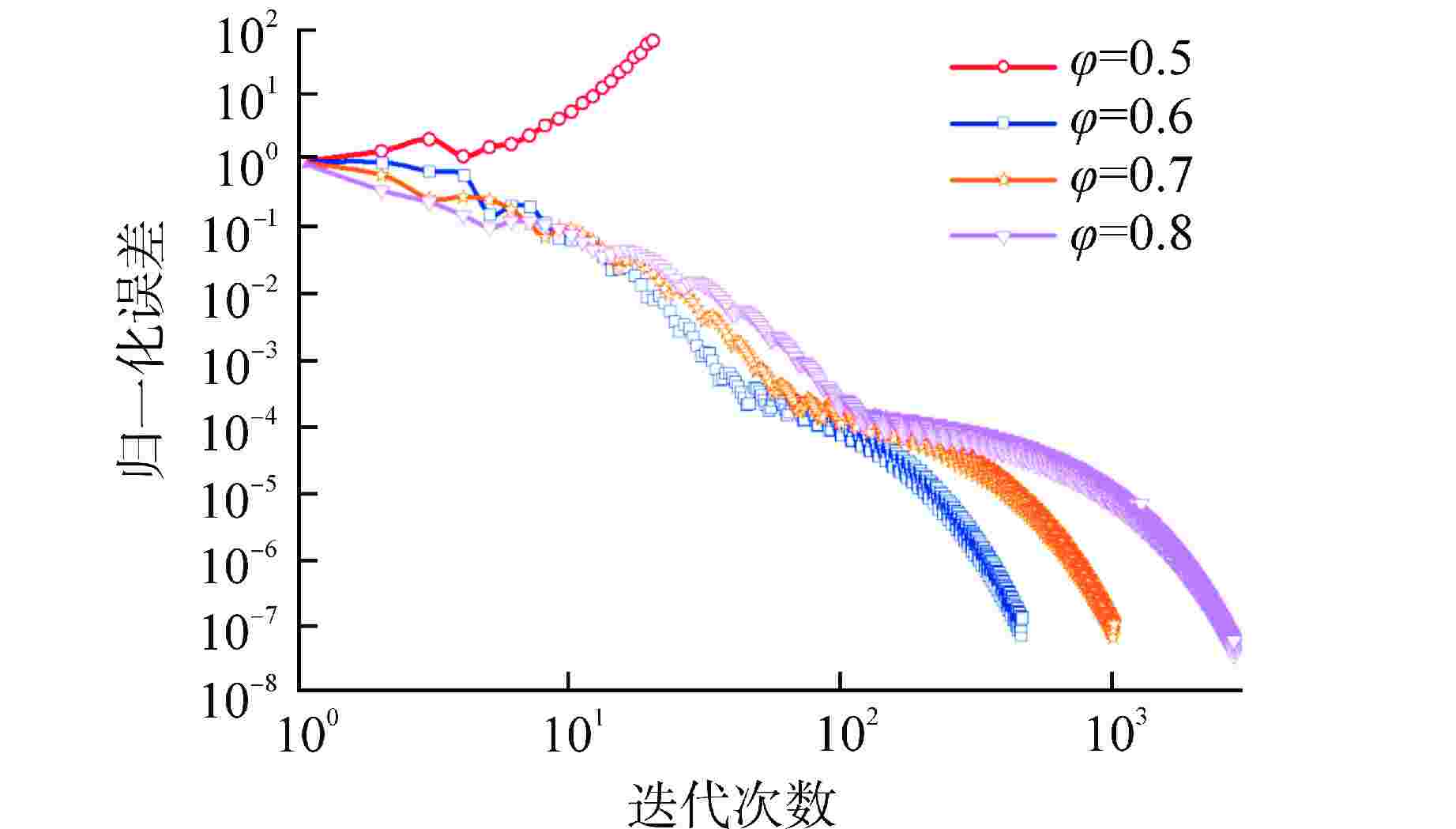
φ	固定点迭代方法		JFNK全局求解方法
φ	固定点迭代步	时间/s	Newton迭代步	时间/s
0.50	无法计算		5	35.9
0.60	454	194.5	5	39.7
0.70	994	422.4	5	39.2
0.80	2376	1172.8	11	54.3

下载: 导出CSV

参考文献(20)

[1]	ROWE D S. COBRA-III: a digital computer program for steady state and transient thermal--hydraulic analysis of rod bundle nuclear fuel elements: BNWL-B-82[R]. Richland: Battelle Pacific Northwest Labs. , 1971.
[2]	ROWE D S. COBRA IIIC: digital computer program for steady state and transient thermal-hydraulic analysis of rod bundle nuclear fuel elements: BNWL-1695[R]. Richland: Battelle Pacific Northwest Labs. , 1973.
[3]	STEWART C W, WHEELER C L, CENA R J, et al. COBRA-IV: the model and the method: BNWL-2214[R]. Richland: Pacific Northwest Laboratories, 1977.
[4]	BASILE D, BEHGI M, CHIERICI R, et al. COBRA-EN: Code System for Thermal-Hydraulic Transient Analysis of Light Water Reactor Fuel Assemblies and Cores: RSICC Code Package PSR-507[R]. U.S.: Oak-Ridge, 2001.
[5]	PLAS R. FLICA III M-reactors or test loops thermohydraulic computer code: CEA-N--2418[R]. Gif-sur-Yvette: CEA Centre d'Etudes Nucleaires de Saclay, 1984.
[6]	DENG J, LU Q, LIU Y, et al. Review of sub-channel code development for pressurized water reactor and introduction of CORTH-V2.0 sub-channel code[J]. Progress in Nuclear Energy, 2020, 125: 103373. doi: 10.1016/j.pnucene.2020.103373
[7]	HU J W, SALKO JR R K, WYSOCKI A J. CTF 4.0 theory manual[R]. Oak Ridge: Oak Ridge National Lab. , 2019.
[8]	TOUMI I, BERGERON A, GALLO D, et al. FLICA-4: a three-dimensional two-phase flow computer code with advanced numerical methods for nuclear applications[J]. Nuclear Engineering and Design, 2000, 200(1-2): 139-155. doi: 10.1016/S0029-5493(99)00332-5
[9]	ESMAILI H, KAZEMINEJAD H, KHALAFI H, et al. Subchannel analysis of annular fuel assembly using the preconditioned Jacobian-free Newton Krylov methods[J]. Annals of Nuclear Energy, 2020, 146: 107616. doi: 10.1016/j.anucene.2020.107616
[10]	PORTER N W. Development of a novel residual formulation of CTF and application of parameter estimation techniques[D]. Raleigh: North Carolina State University, 2018.
[11]	PORTER N W, MOUSSEAU V A, AVRAMOVA M N. CTF-R: a novel residual-based thermal hydraulic solver[J]. Nuclear Engineering and Design, 2019, 348: 37-45. doi: 10.1016/j.nucengdes.2019.04.006
[12]	PLAS R. FLICA III M-reactors or test loops thermohydraulic computer code[R]. Gif-sur-Yvette: CEA Centre d'Etudes Nucleaires de Saclay, 1984.
[13]	MOORTHI A, SHARMA A K, VELUSAMY K. A review of sub-channel thermal hydraulic codes for nuclear reactor core and future directions[J]. Nuclear Engineering and Design, 2018, 332: 329-344. doi: 10.1016/j.nucengdes.2018.03.012
[14]	KNOLL D A, KEYES D E. Jacobian-free Newton–Krylov methods: a survey of approaches and applications[J]. Journal of Computational Physics, 2004, 193(2): 357-397. doi: 10.1016/j.jcp.2003.08.010
[15]	CHAN T F, VAN DER VORST H A. Approximate and incomplete factorizations[M]//KEYES D E, SAMEH A, VENKATAKRISHNAN V. Parallel Numerical Algorithms. Dordrecht: Springer, 1997: 167-202.
[16]	ZHOU X F, ZHONG C M, ZHANG Y Y. Jacobian-free Newton Krylov two-node coarse mesh finite difference based on nodal expansion method for multiphysics coupled models[J]. Annals of Nuclear Energy, 2022, 168: 108915. doi: 10.1016/j.anucene.2021.108915
[17]	EISENSTAT S C, WALKER H F. Choosing the forcing terms in an inexact Newton method[J]. SIAM Journal on Scientific Computing, 1996, 17(1): 16-32. doi: 10.1137/0917003
[18]	PERNICE M, WALKER H F. NITSOL: a Newton iterative solver for nonlinear systems[J]. SIAM Journal on Scientific Computing, 1998, 19(1): 302-318. doi: 10.1137/S1064827596303843
[19]	广东核电培训中心. 900MW压水堆核电站系统与设备[M]. 北京: 原子能出版社, 2005: 611.
[20]	梁志滔. 压水堆核电站堆芯子通道分析[D]. 广州: 华南理工大学, 2011.