Experimental Investigation on Void Fraction Distribution of Boiling Flow in 2×2 Rod Bundle Channel
-
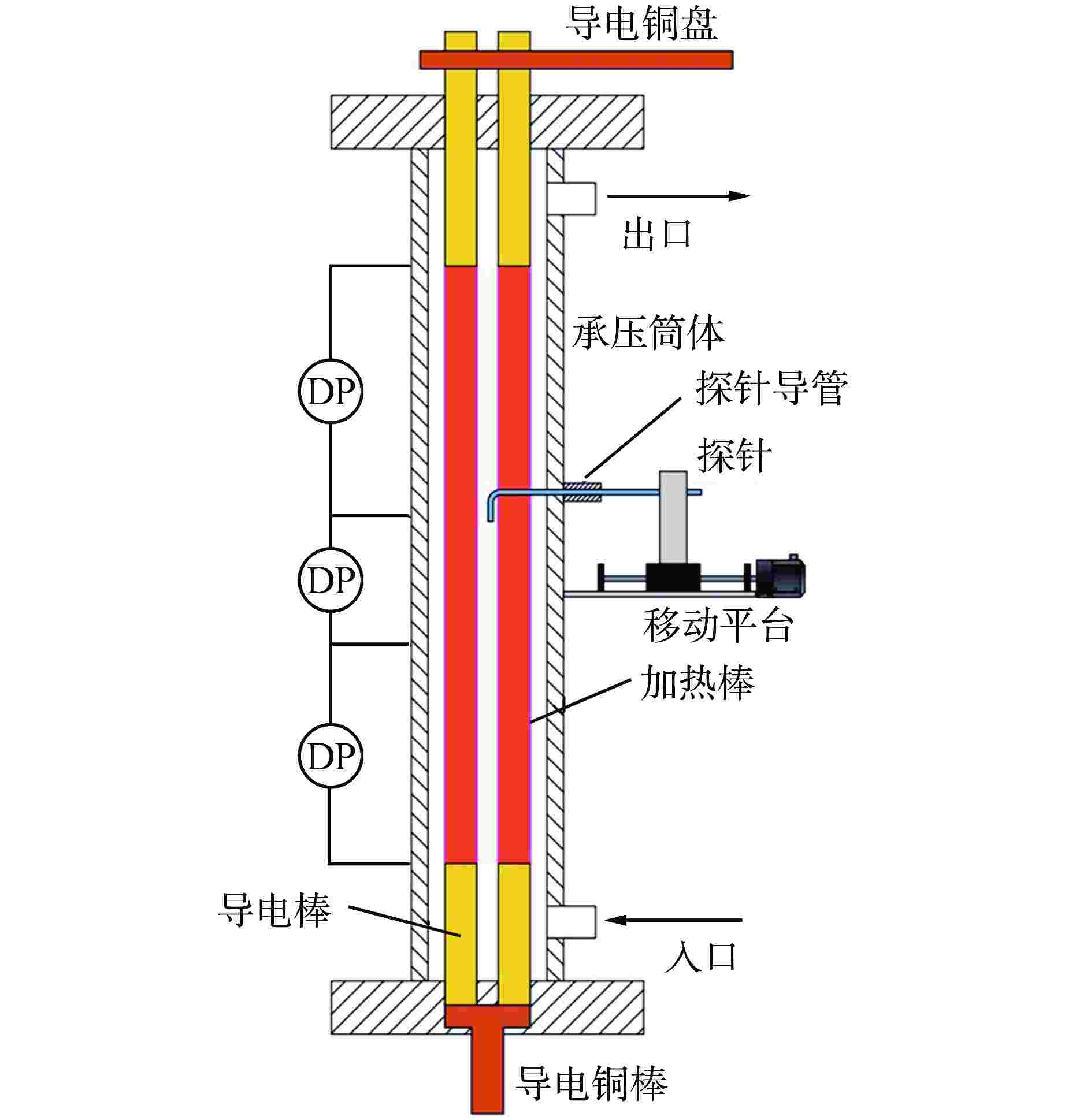
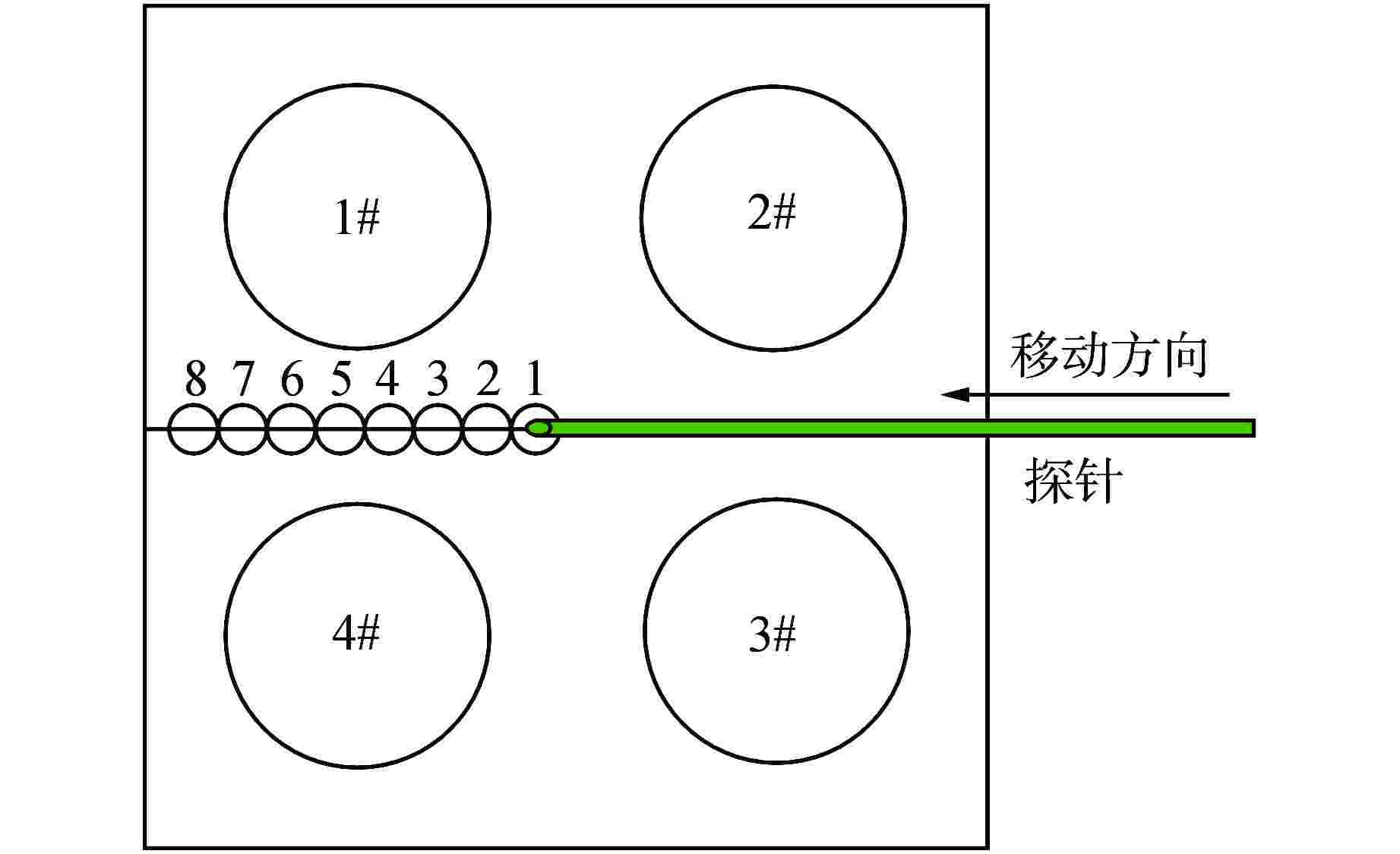
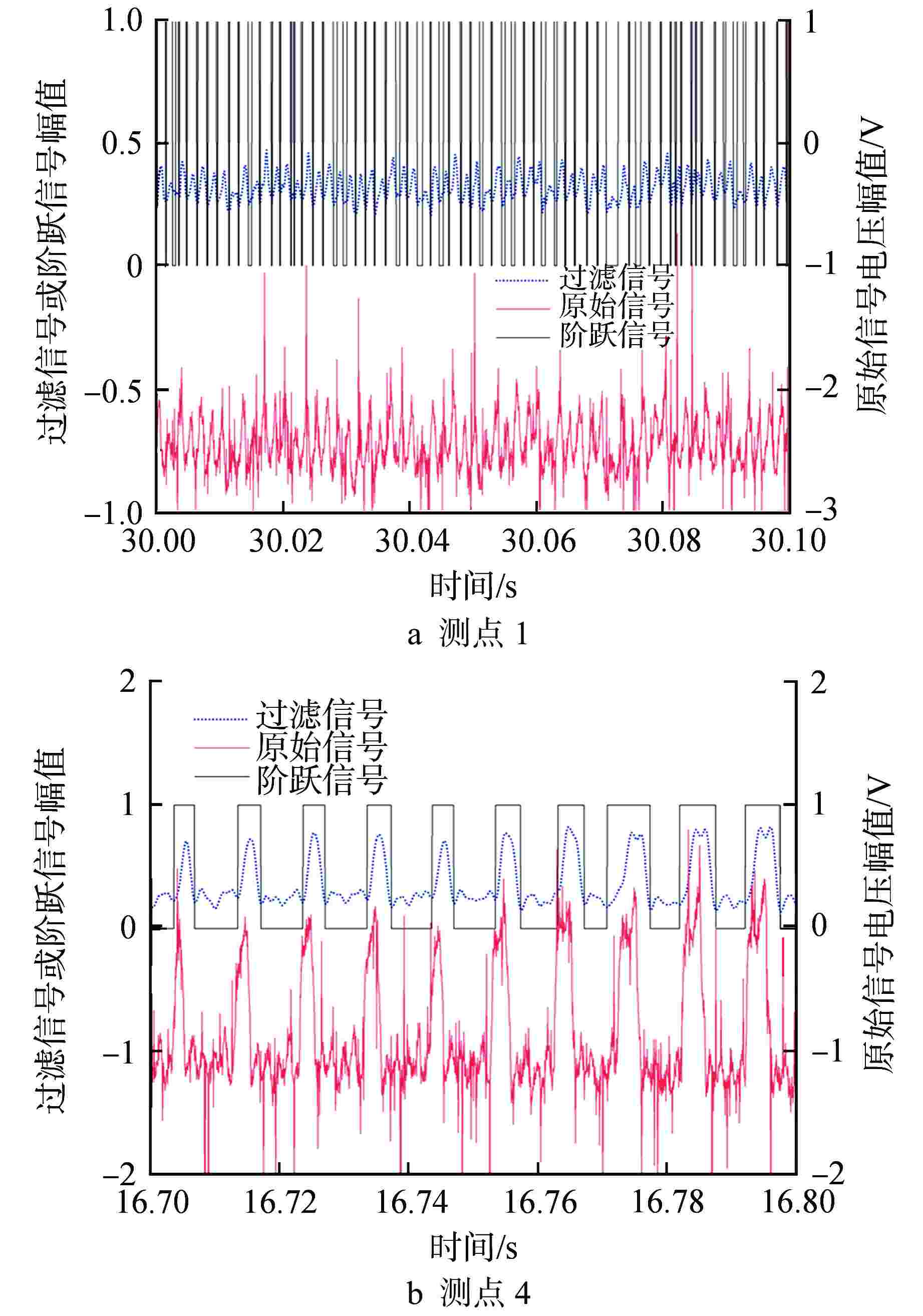
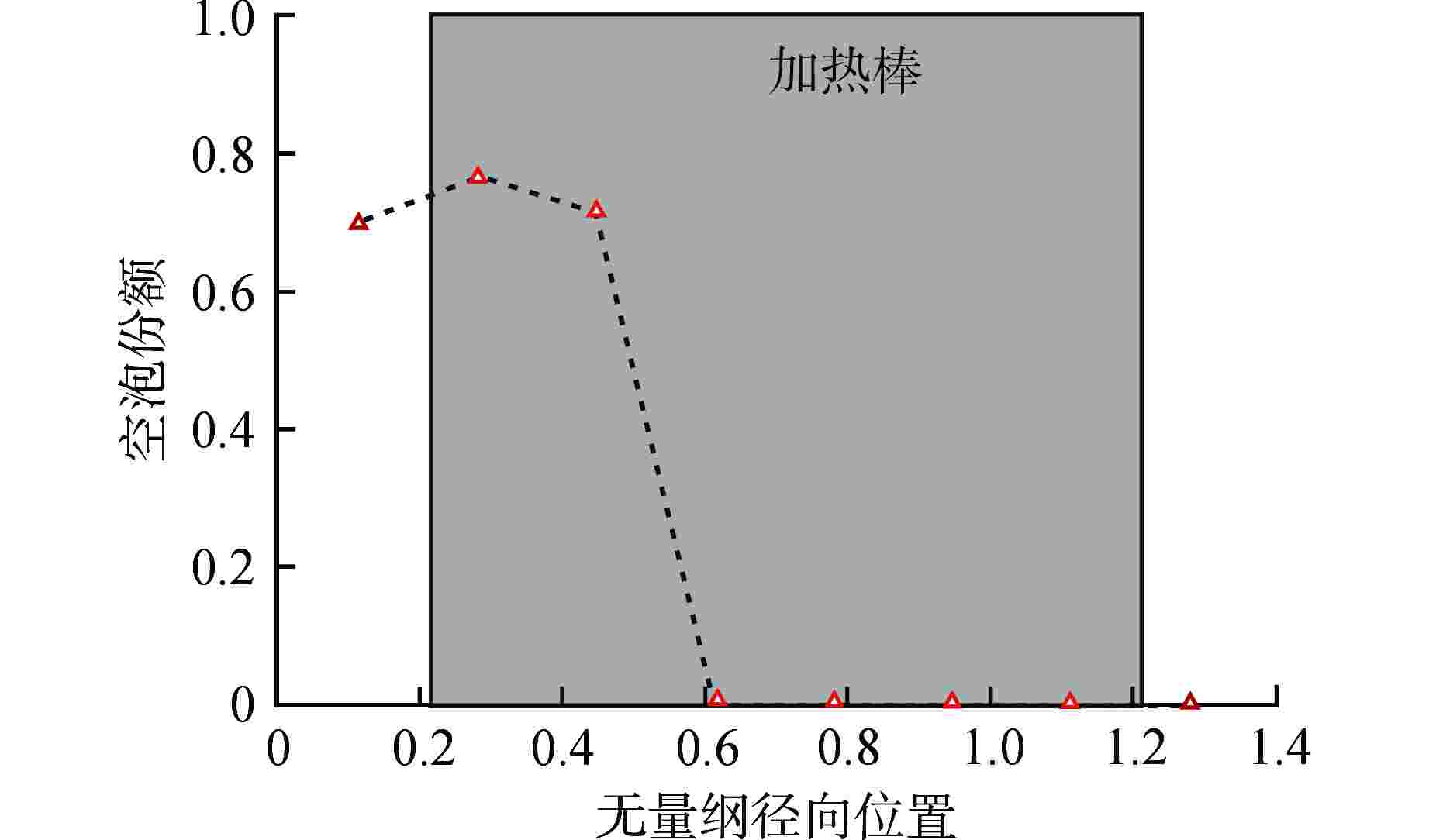
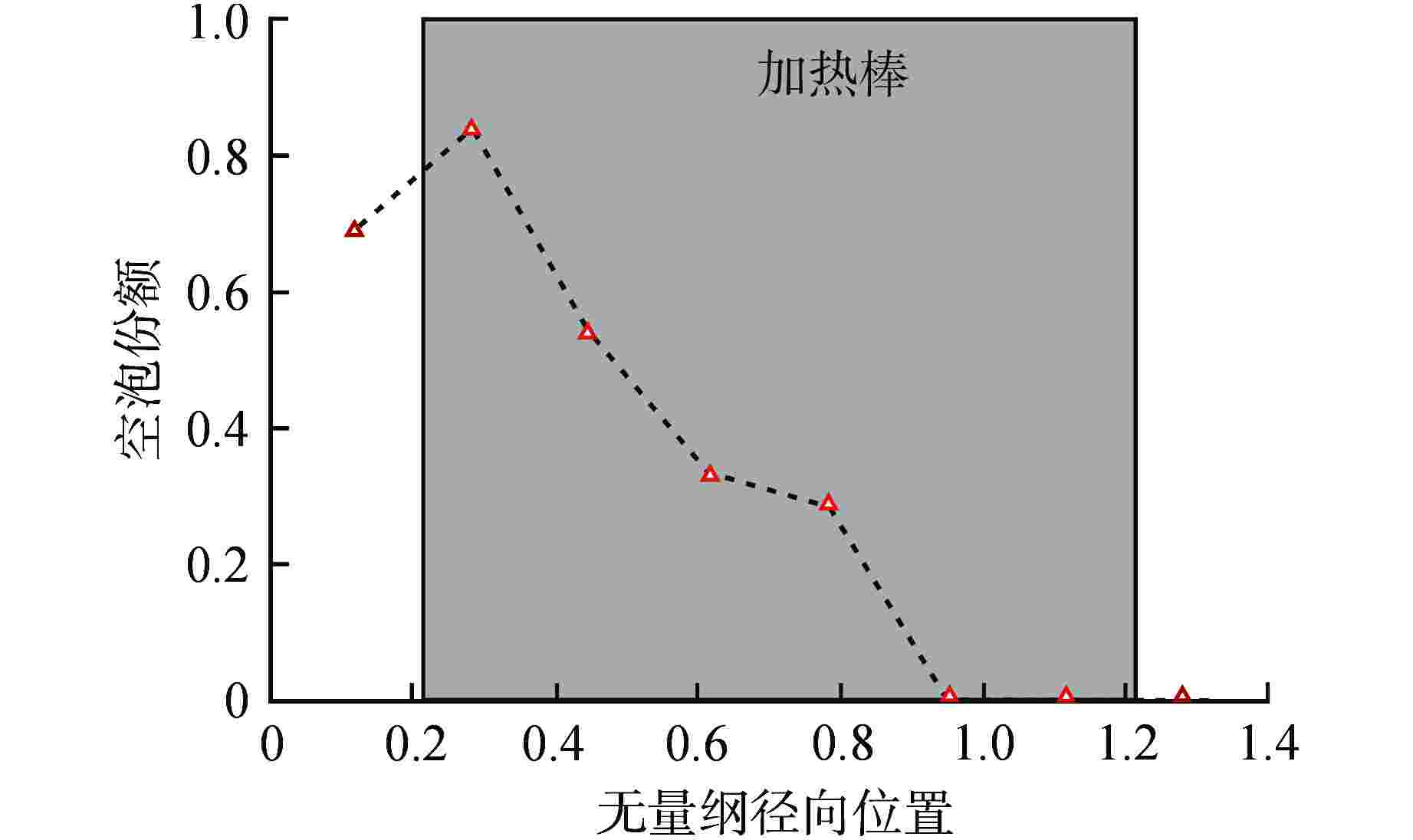
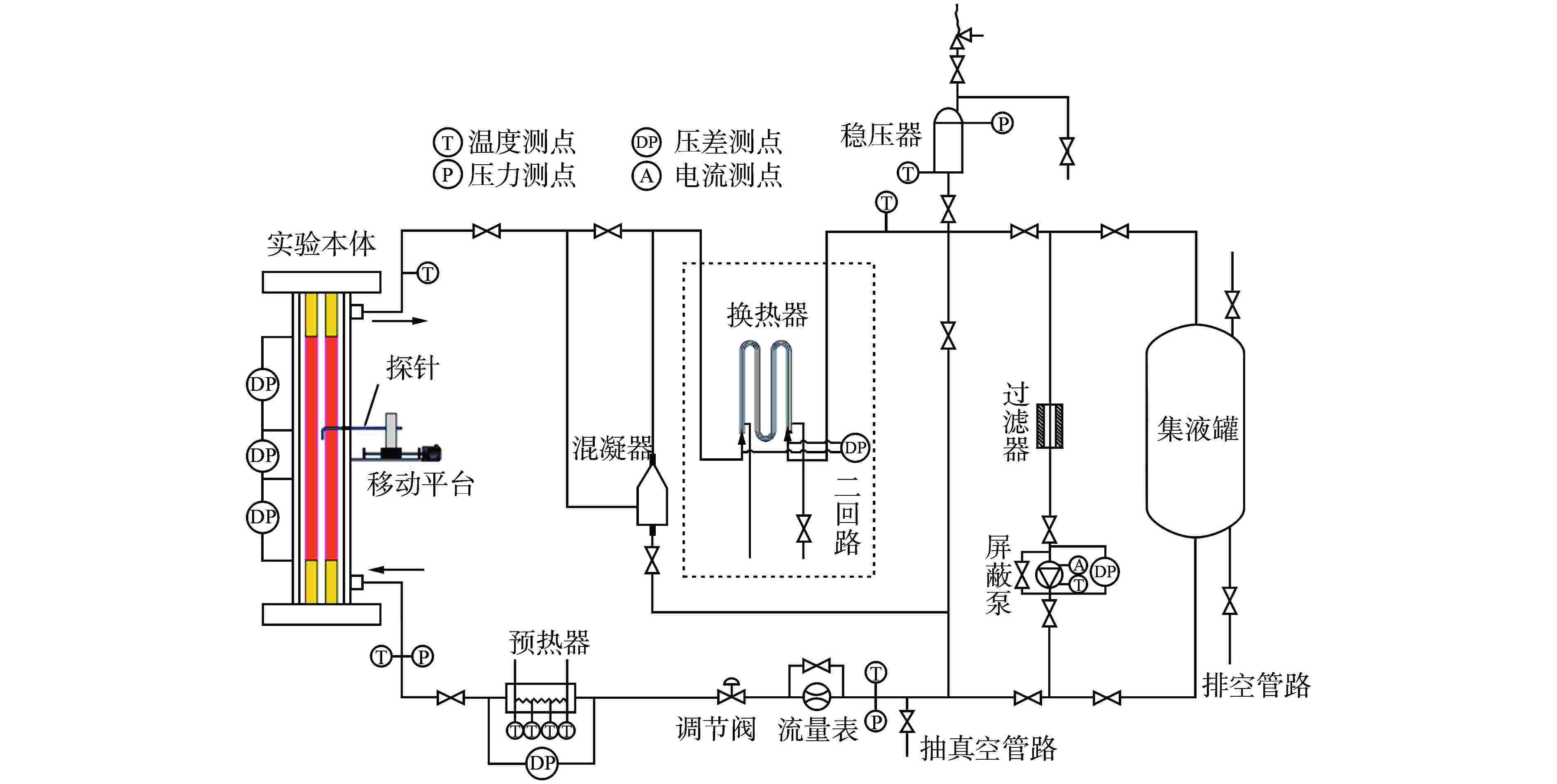
摘要: 电导探针方法是一种获取两相界面参数的重要手段。通过单探头电导探针测量并分析了2×2棒束通道内流动沸腾空泡份额的径向分布,结果表明,在当前实验工况下,从汽泡信号的波动特性来看,通道中心处的汽泡信号主体波动幅度较小,棒间隙处的汽泡信号主体波动幅度较大;空泡份额径向分布均呈现出中心峰的分布特性,中心峰呈现出下凹的现象,这是由于中心处的汽泡相对于壁面处的汽泡吸收的热量更小而发生冷凝。Abstract: The conductivity probe method is an important methodology to obtain two-phase interfacial parameters. The radial distribution of the boiling flow void fraction in the 2 × 2 rod bundle channel was measured and analyzed by a one-sensor conductivity probe. The results show that under the current experimental conditions, from the fluctuation characteristics of the bubble signal, the fluctuation amplitude of the bubble signal main body at the center of the channel is small, and the fluctuation amplitude of the bubble signal main body at the rod gap is large. The radial distribution of void fraction shows the distribution characteristics of the core peak, and the core peak shows a concave phenomenon, which is due to the bubble at the center receives less heat than that at the wall.
-
Key words:
- Conductivity probe,
- Rod bundle channel,
- Boiling flow,
- Void fraction
-
表 1 棒束通道实验工况
Table 1. Experimental Conditions of Rod Bundle Channel
工况
序号压力/
MPa质量流速/
(kg·m−2·s−1)入口过冷度/
K热流密度/
(kW·m−2)1 0.33 824.40 27.10 590 2 0.33 825.86 27.80 605 3 0.33 822.93 21.90 590 表 2 原始汽泡信号主体电压振幅和单个阶跃信号的时间跨度
Table 2. Time Span of Original Bubble Signal Main Body Amplitude and Single Step Signal
工况序号 测点1 测点4 电压振幅/V 时间跨度/ms 电压振幅/V 时间跨度/ms 1 0~0.5 1.2~3.0 0 0 2 0~0.5 1.5~3.0 0~1 3.0~8.0 3 0~0.5 1.0~3.0 0~1.5 5.0~8.0 表 3 滑速比模型
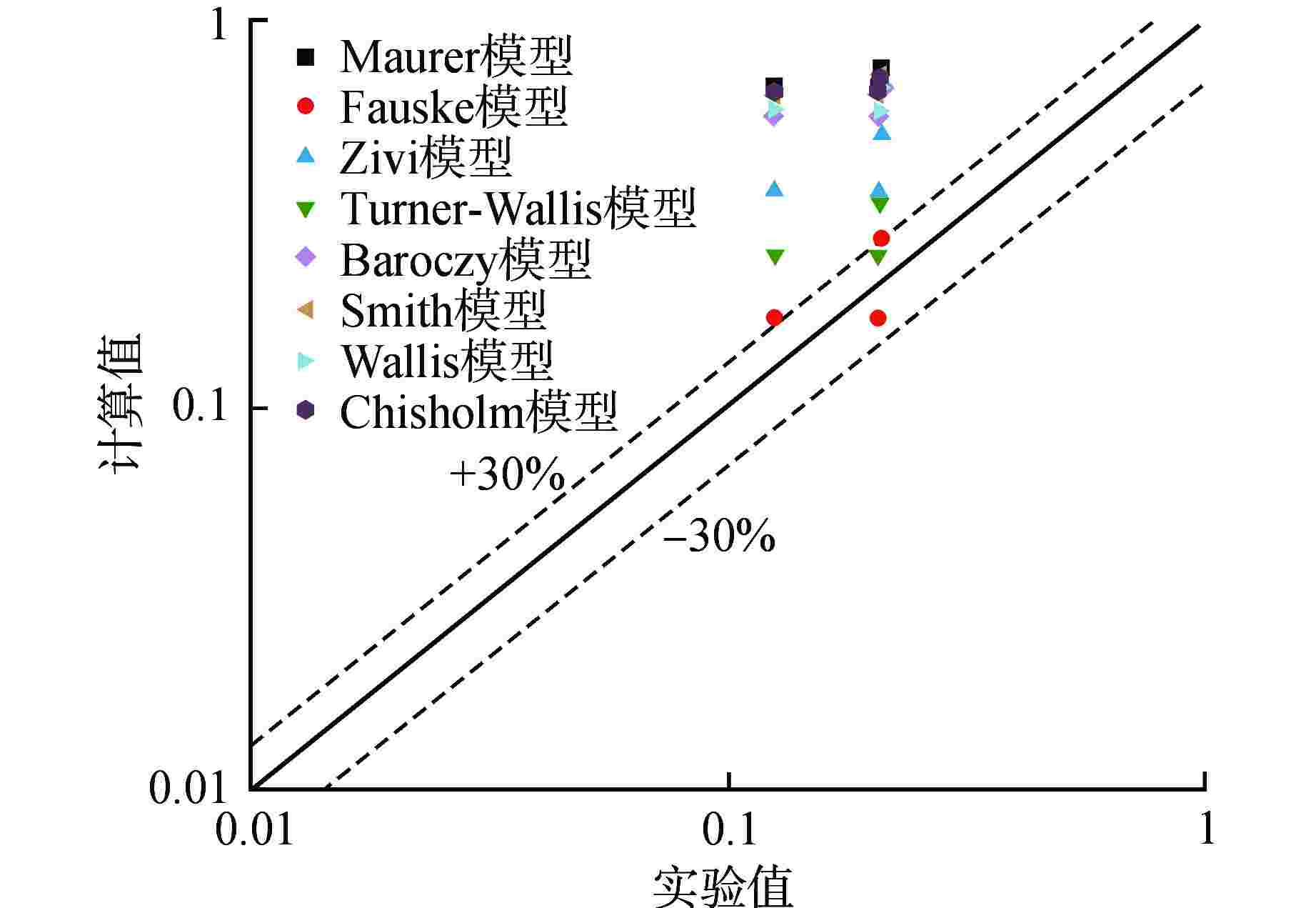
Table 3. Slip Ratio Model
学者 表达式 Maurer[20] $\alpha = \dfrac{1}{{1 + 0.8{{\left( {\dfrac{{1 - x}}{x}} \right)}^{0.6819 + 0.01217p}}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{0.6}}}}$ Fauske[21] $\alpha = \dfrac{1}{{1 + \dfrac{{1 - x}}{x}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{1/2}}}}$ Zivi[22] $\alpha = \dfrac{1}{{1 + \dfrac{{1 - x}}{x}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{2/3}}}}$ Turner-
Wallis[23]$ \alpha = \dfrac{1}{{1 + {{\left[ {{{\left( {\dfrac{{{\mu _{\text{f}}}}}{{{\mu _{\text{g}}}}}} \right)}^{0.1}}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{0.5}}{{\left( {\dfrac{{1 - x}}{x}} \right)}^{0.9}}} \right]}^{0.8}}}} $ Baroczy[24] $\alpha = {\left[ {1 + {{\left( {\dfrac{{1 - x}}{x}} \right)}^{0.72}}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{0.65}}{{\left( {\dfrac{{{\mu _{\text{f}}}}}{{{\mu _{\text{g}}}}}} \right)}^{0.13}}} \right]^{ - 1}}$ Smith[25] $\alpha = {\left\{ {1 + 0.4\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}\left( {\dfrac{1}{x} - 1} \right) + 0.6\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}\left( {\dfrac{1}{x} - 1} \right){{\left[ {\dfrac{{{\rho _{\text{f}}}/{\rho _{\text{g}}} + 0.4(1/x - 1)}}{{1 + 0.4(1/x - 1)}}} \right]}^{1/2}}} \right\}^{ - 1}}$ Wallis[26] $ \alpha = {\left\{ {1 + {{\left[ {{{\left( {\dfrac{{{\mu _{\text{f}}}}}{{{\mu _{\text{g}}}}}} \right)}^{0.1}}{{\left( {\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}} \right)}^{0.5}}{{\left( {\dfrac{{1 - x}}{x}} \right)}^{0.9}}} \right]}^{0.8}}} \right\}^{ - 0.38}} $ Chisholm[27] $\alpha = \dfrac{1}{{1 + \dfrac{{1 - x}}{x}\dfrac{{{\rho _{\text{g}}}}}{{{\rho _{\text{f}}}}}\sqrt {1 - x\left( {1 - \dfrac{{{\rho _{\text{f}}}}}{{{\rho _{\text{g}}}}}} \right)} }}$ α—空泡份额;p—压力,MPa; $ {\rho _{\text{g}}} $—气相密度,kg/m3; $ {\rho _{\text{f}}} $—液相密度,kg/m3; $ {\mu _{\text{g}}} $—气相粘度,Pa∙s; $ {\mu _{\text{f}}} $—液相粘度,Pa∙s 表 4 汽泡尺寸计算结果
Table 4. Calculation Results of Bubble Size
工况序号 测点1 测点4 时间跨
度/ms基于Fauske模型的
汽泡尺寸/mm时间跨
度/ms基于Fauske模型的
汽泡尺寸/mm1 1.2~3.0 23.7~59.2 0 0 2 1.5~3.0 29.6~59.2 3.0~8.0 59.2~157.9 3 1.0~3.0 19.7~59.2 5.0~8.0 98.7~157.9 -
[1] ISHII M, HIBIKI T. Thermo-fluid dynamics of two-phase flow[M]. 2nd ed. New York: Springer, 2011: 518. [2] OZAR B, BROOKS C S, HIBIKI T, et al. Interfacial area transport of vertical upward steam–water two-phase flow in an annular channel at elevated pressures[J]. International Journal of Heat and Mass Transfer, 2013, 57(2): 504-518. doi: 10.1016/j.ijheatmasstransfer.2012.10.059 [3] PRASSER H M, KREPPER E, LUCAS D. Evolution of the two-phase flow in a vertical tube—decomposition of gas fraction profiles according to bubble size classes using wire-mesh sensors[J]. International Journal of Thermal Sciences, 2002, 41(1): 17-28. doi: 10.1016/S1290-0729(01)01300-X [4] TOMIYAMA A, TAMAI H, ZUN I, et al. Transverse migration of single bubbles in simple shear flows[J]. Chemical Engineering Science, 2002, 57(11): 1849-1858. doi: 10.1016/S0009-2509(02)00085-4 [5] LUCAS D, KREPPER E, PRASSER H M. Development of co-current air–water flow in a vertical pipe[J]. International Journal of Multiphase Flow, 2005, 31(12): 1304-1328. doi: 10.1016/j.ijmultiphaseflow.2005.07.004 [6] 徐济鋆. 沸腾传热和气液两相流[M]. 第二版. 北京: 原子能出版社, 2001: 388. [7] AGOSTINI G, ERA A, PREMOLI A. Density measurements of steam- water mixtures flowing in a tubular channel under adiabatic and heated conditions[J]. Energia Nucleare, 1971, 18(5): 295-310. [8] ANKLAM T M, MILLER R F. Void fraction under high pressure, low flow conditions in rod bundle geometry[J]. Nuclear Engineering and Design, 1983, 75(1): 99-108. doi: 10.1016/0029-5493(83)90083-3 [9] ANODA Y, KUKITA Y, TASAKA K. Void fraction distribution on rod bundle under high pressure conditions[C]// American Society of Mechanical Engineers. Proceedings of the ASME Winter Annual Meeting. US: American Society of Mechanical Engineers.1990: 283-289. [10] YUN B J, SIM S K, HWANG S H, et al. Local characteristics of two-phase flow parameters in an annulus boiling channel[J]. KSME International Journal, 1997, 11(4): 443-456. doi: 10.1007/BF02945083 [11] YUN B J, PARK G C, JULIA J E, et al. Flow structure of subcooled boiling water flow in a subchannel of 3×3 rod bundles[J]. Journal of Nuclear Science and Technology, 2008, 45(5): 402-422. doi: 10.1080/18811248.2008.9711450 [12] YANG X, SCHLEGEL J P, LIU Y, et al. Measurement and modeling of two-phase flow parameters in scaled 8×8 BWR rod bundle[J]. International Journal of Heat and Fluid Flow, 2012, 34: 85-97. doi: 10.1016/j.ijheatfluidflow.2012.02.001 [13] YANG X, SCHLEGEL J P, LIU Y, et al. Experimental study of interfacial area transport in air–water two phase flow in a scaled 8×8 BWR rod bundle[J]. International Journal of Multiphase Flow, 2013, 50: 16-32. doi: 10.1016/j.ijmultiphaseflow.2012.10.006 [14] REN Q Y, PAN L M, ZHOU W X, et al. Phase distribution characteristics of bubbly flow in 5 × 5 vertical rod bundles with mixing vane spacer grids[J]. Experimental Thermal and Fluid Science, 2018, 96: 451-459. doi: 10.1016/j.expthermflusci.2018.04.002 [15] SHEN X Z, MIWA S, XIAO Y G, et al. Local measurements of upward air-water two-phase flows in a vertical 6×6 rod bundle[J]. Experimental and Computational Multiphase Flow, 2019, 1(3): 186-200. doi: 10.1007/s42757-019-0031-0 [16] BOTTINI J L, ZHU L X, OOI Z J, et al. Experimental study of boiling flow in a vertical heated annulus with local two-phase measurements and visualization[J]. International Journal of Heat and Mass Transfer, 2020, 155: 119712. doi: 10.1016/j.ijheatmasstransfer.2020.119712 [17] OOI Z J, BROOKS C S. Beyond time-averaged measurement of bubble parameters in steam-water flows with conductivity probes[J]. International Journal of Multiphase Flow, 2021, 138: 103594. doi: 10.1016/j.ijmultiphaseflow.2021.103594 [18] HIBIKI T, HOGSETT S, ISHII M. Local measurement of interfacial area, interfacial velocity and liquid turbulence in two-phase flow[J]. Nuclear Engineering and Design, 1998, 184(2-3): 287-304. doi: 10.1016/S0029-5493(98)00203-9 [19] SAHA P, ZUBER N. Point of net vapor generation and vapor void fraction in subcooled boiling[C]//Proceedings of the International Heat Transfer Conference 5. Tokyo: IHTC, 1974: 175-179. [20] MAURER G. A method of predicting steady-state boiling vapor fractions in reactor coolant channels[J]. Bettis Technical Review, 1960, WAPD-BT-19: 59-70. [21] FAUSKE H. Critical two-phase, steam-water flows[C]//Proceedings of the the 1961 Heat Transfer and Fluid Mechanics Institute. Stanford: Stanford University Press, 1961: 79-89. [22] ZIVI S M. Estimation of steady-state steam void-fraction by means of the principle of minimum entropy production[J]. Journal of Heat Transfer, 1964, 86(2): 247-251. doi: 10.1115/1.3687113 [23] TURNER J M, WALLIS G B. The separate-cylinders model of two-phase flow: NSA-19-040737[R]. Hanover: Thayer School of Engineering, Dartmouth College, 1965. [24] BAROCZY C J. A systematic correlation for two-phase pressure drop[J]. Chemical Engineering Progress Symposium Series, 1966, 64: 232-249. [25] SMITH S L. Void fractions in two-phase flow: a correlation based upon an equal velocity head model[J]. Proceedings of the Institution of Mechanical Engineers, 1969, 184(1): 647-664. doi: 10.1243/PIME_PROC_1969_184_051_02 [26] WALLIS G B. One-dimensional two-phase flow[M]. New York: McGraw-Hill, 1969: 408. [27] CHISHOLM D. Pressure gradients due to friction during the flow of evaporating two-phase mixtures in smooth tubes and channels[J]. International Journal of Heat and Mass Transfer, 1973, 16(2): 347-358. doi: 10.1016/0017-9310(73)90063-X [28] ISHII M. One-dimensional drift-flux model and constitutive equations for relative motion between phases in various two-phase flow regimes: ANL-77-47[R]. Argonne: Argonne National Laboratory, 1978. [29] ISHII M, ZUBER N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows[J]. AIChE Journal, 1979, 25(5): 843-855. doi: 10.1002/aic.690250513 [30] KIM S, FU X Y, WANG X, et al. Development of the miniaturized four-sensor conductivity probe and the signal processing scheme[J]. International Journal of Heat and Mass Transfer, 2000, 43(22): 4101-4118. doi: 10.1016/S0017-9310(00)00046-6 [31] REN Q Y, PAN L M, PU Z P, et al. Two-group phase distribution characteristics for air-water flow in 5×5 vertical rod bundle channel with mixing vane spacer grids[J]. International Journal of Heat and Mass Transfer, 2021, 176: 121444. doi: 10.1016/j.ijheatmasstransfer.2021.121444 [32] ZHANG H W, XIAO Y, GU H Y. Experimental investigation of two-phase flow evolution in a tight lattice bundle using wire-mesh sensor[J]. International Journal of Heat and Mass Transfer, 2021, 171: 121079. doi: 10.1016/j.ijheatmasstransfer.2021.121079 -





 下载:
下载: