Prediction and Analysis of Heat Transfer Characteristics of Supercritical Fluids Based on Interpretable Machine Learning
-
摘要: 超临界流体在拟临界温度附近发生剧烈的物性变化,传热特性难以准确预测。本研究采用可解释机器学习的研究方法预测并分析超临界流体传热特性。使用粒子群优化算法(PSO)搜索反向传播神经网络(BPNN)模型最优超参数,建立了超临界流体传热预测模型,并与传统经验关联式进行了精度比较。使用SHAP可解释算法对BPNN模型进行了全局和局部解释,根据不同工况下特征重要度的变化发现超临界相关机理现象。结果显示,所建立的神经网络模型在测试集上的平均绝对百分比误差(MAPE)为1.4%,决定系数R2为0.9992,与经验关联式相比,该模型具有更高的预测精度;对于垂直向上流动,浮升力效应在传热恶化工况中明显具有更高的特征重要度,是传热恶化行为发生的主要因素。因此,本研究建立的基于可解释机器学习的研究方法对进一步研究超临界流体传热特性具有一定的参考意义。Abstract: The physical properties of supercritical fluids change drastically near the pseudo-critical temperature, making it challenging to accurately predict heat transfer characteristics. In this study, the method of interpretable machine learning was used to predict and analyze the heat transfer characteristics of supercritical fluids. The particle swarm optimization algorithm (PSO) was used to search for the optimal hyperparameters of the back propagation neural network (BPNN) model, the supercritical fluid heat transfer prediction model was established, and its accuracy was compared with the traditional empirical correlation. The global and local interpretation of the BPNN model was carried out by using the SHAP interpretable algorithm, and the supercritical correlation phenomenon and mechanism were found according to the change of feature importance under different conditions. The results show that the MAPE of the established neural network model on the test set is 1.4%, and the coefficient of determination R2 is 0.9992, which has higher prediction accuracy compared with the empirical correlation formula. For vertical upward flow, buoyancy effect obviously has higher feature importance in heat transfer deterioration condition, which is the main factor of heat transfer deterioration behavior. Therefore, the research method based on interpretable machine learning established in this study has certain reference significance for further study of the heat transfer characteristics of supercritical fluids.
-
0. 引 言
超临界流体由于其独特的热力学及输运性质,被认为是提高动力循环和能量转换热效率的工质,并已在航空航天、核电、太阳能、制冷、地热能、化工技术等工程领域应用[1]。超临界流体的物性会在拟临界温度附近发生剧烈的非线性变化,包括比热的急剧增加、动力粘度和密度急剧下降等。虽然偏离核态沸腾(DNB)现象在超临界压力下不会发生,但在特定质量流速和热流密度组合下,可能发生传热恶化(HTD),从而导致壁温过高。这对于应用场景系统的设计和安全带来巨大挑战,因此对超临界流体传热特性研究至关重要。
目前对于超临界流体传热预测的研究大多采用经验关联式的方法。大多数关联式在传统的Dittus-Boelter关联式或Ginielinski关联式的基础上,引入物性比、浮升力因子、加速度因子等参数用于表征超临界传热中的特殊效应[2-8]。然而引入参数与预测参数之间存在高度非线性的关系,限制了经验关联式拟合的准确性。另外,部分研究采用数值模拟的方法获得流场信息并预测超临界流体的传热系数[9-15],而湍流模型的可靠性决定了计算流体动力学(CFD)模拟的准确性[15],目前针对超临界流体拟临界区传热的湍流模型开发还比较欠缺。此外,直接数值模拟(DNS)通常需要高性能的计算资源,限制了其在超临界传热预测中的实际应用。因此有必要探索新的超临界流体传热预测方法。
近年来,随着人工智能的快速发展,人工神经网络(ANN)由于具有优异的自学习、自适应、容错性、非线性拟合等特性,一些研究将其应用于超临界传热预测,并表现出了预测精度高、应用范围广、便捷性强等优势。Zhang等[16]建立了一个同时预测超临界H2O和CO2的壁面温度和努塞尔数Nu的通用ANN模型,是目前第一个可用于多流体的超临界传热预测模型,对Nu进行预测,对于CO2决定系数R2为0.974;对于H2O,R2为0.970。Amardeep等[17]利用超临界水在垂直上升管道中换热的CFD模拟数据,利用ANN对Nu进行预测,平均绝对百分比误差(MAPE)达到1.46%。Ma等[18]在低热流密度工况下,建立了超临界水传热系数预测的反向传播神经网络(BPNN)模型,R2为0.971。Sun等[19]使用遗传算法优化反向传播神经网络(GA-BP)的初始参数,建立了GA-BP模型对管内超临界CO2流动传热的Tw进行预测,均方根误差(RMSE)达到1.03℃,R2达到0.99。Pesteei等[20]采用数据处理组法(GMDH)模型预测了雷诺数Re<2500条件下垂直管内超临界CO2的局部换热特性,RMSE=25.643 kW/(m2·K),R2=0.984。以上研究表明,神经网络模型能够为超临界流体复杂的换热行为和传热特性提供更为准确的预测。
然而,ANN是一种“黑盒模型”,模型的内部逻辑和预测机制对用户是隐藏的,从而阻止了对于其决策行为的解释和推理,这种不可解释性将大大影响模型应用的可信度和可靠性,阻碍人们从模型中获取知识[21]。
因此,本研究基于可解释机器学习的方法,将可解释算法与BPNN相结合,一方面建立超临界流体传热预测模型,提供较为准确的超临界传热预测,另一方面通过BPNN模型挖掘数据内部的价值,发现超临界相关机理现象,为揭示超临界传热机理提供新的视角。
1. 数据与方法
本研究采用上海交通大学超临界水流动传热实验数据,流动方向为垂直向上,管道形状为圆形,工况参数覆盖范围为:压力P为23~30 MPa,质量流量G为600~1500 kg/(m2·s),热流密度q为200~1400 kW/m2,管径d为7.6~26 mm,主流温度Tb为210.84~449.29℃。实验数据包含1598个样本点。
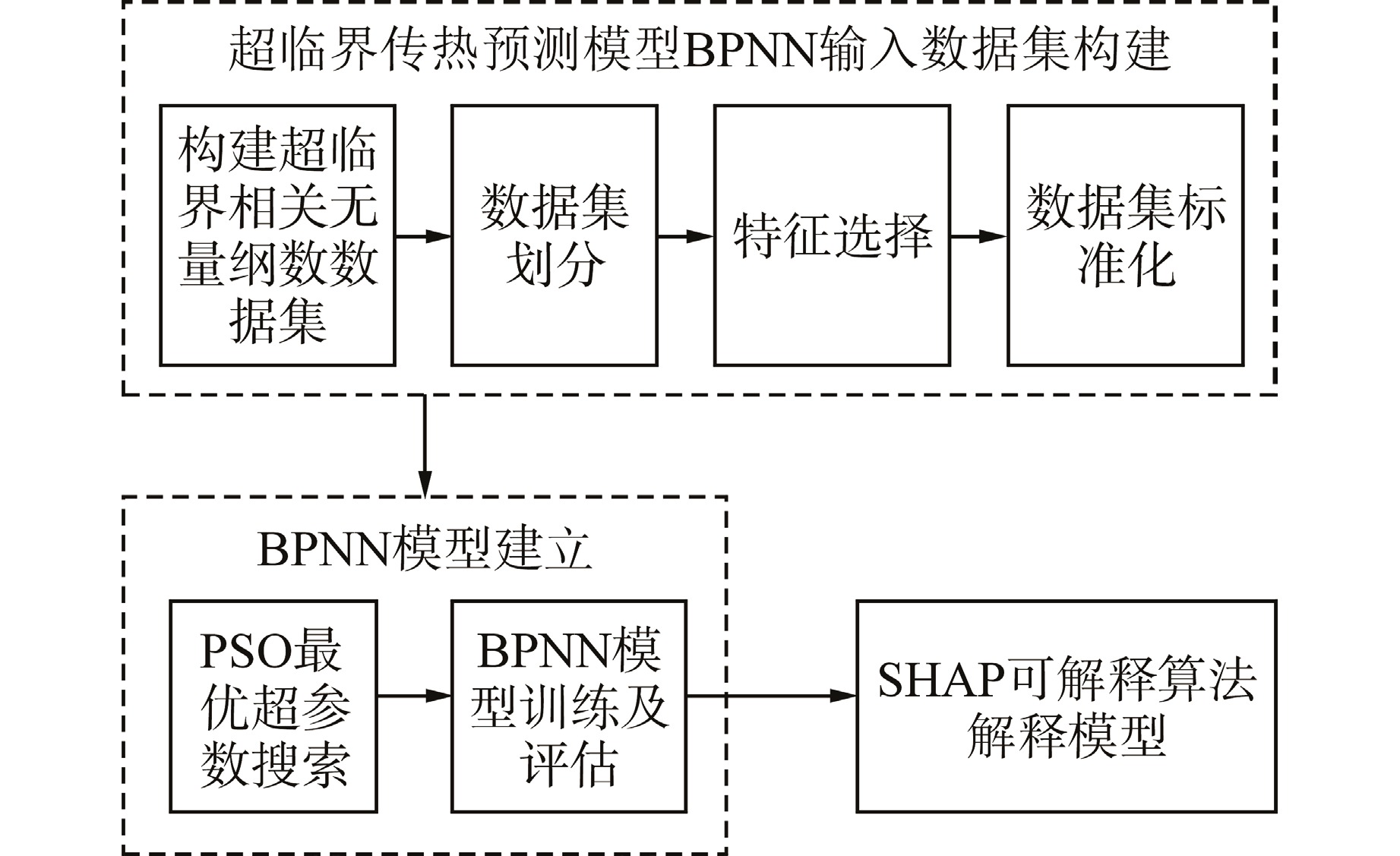
研究流程如图1所示,通过REFPROP物性包获取流体的热物性数据,对选择的与超临界传热相关的无量纲数进行计算构建数据集。随机划分80%的数据为训练集,20%的数据为测试集。采用Spearman相关系数法进行特征选择,选择后的特征作为BPNN模型的输入参数,Nu作为模型的输出参数。采用Z-Score标准化处理训练集和测试集上的数据。离线阶段采用粒子群优化算法(PSO)对模型进行超参数寻优,在线阶段对模型进行训练和评估。最后使用SHAP可解释算法对模型进行全局和局部解释,根据不同工况下特征重要度的变化研究超临界传热机理现象。
1.1 超临界传热预测模型BPNN输入数据集建立
对于超临界流体流动传热,考虑了21个无量纲数见表1。其中,$B{u_2}$参数由Jackson[22]提出,用于描述垂直管中的超临界传热浮力效应;$B{u_1}$参数由Jiang等[23]提出,也是评估垂直管中浮力效应的显著依据;Liu等[24]根据浮力效应引起的剪切力变化推导出$B{u_3}$参数。
表 1 特征选择前的无量纲数Table 1. Dimensionless Number before Feature Selection序号 无量纲数 序号 无量纲数 1 $R{e_{\text{b}}}$ 12 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{w}}}}}}$ 2 $P{r_{\text{b}}}$ 13 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{b}}}}}}$ 3 $R{e_{\text{w}}}$ 14 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{w}}}}}}$ 4 $R{e_{\text{f}}}$ 15 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{{\text{pc}}}}}}$ 5 $P{r_{\text{w}}}$ 16 $\dfrac{{{k_{\text{b}}}}}{{{k_{{\text{pc}}}}}}$ 6 ${\overline {Pr} _{\text{b}}}$ 17 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{pc}}}}}}$ 7 ${\overline {Pr} _{\text{w}}}$ 18 $ Gr_{\text{b}}=\dfrac{\left(\rho_{\text{b}}-\rho_{\text{w}}\right)gd^3}{\rho_{\text{b}}\mathit{\upsilon}_{\text{b}}^2} $ 8 $\dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{w}}}}}$ 19 $B{u_1} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^2}}$ 9 $\dfrac{{{k_{\text{b}}}}}{{{k_{\text{w}}}}}$ 20 $B{u_2} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.7}}}$ 10 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}$ 21 $B{u_3} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.625}Pr_{\text{w}}^{{\text{0}}{\text{.4}}}}}{\left( {\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\text{w}}}}}{{{\mu _{\text{b}}}}}} \right)$ 11 $\dfrac{{{\nu _{\text{b}}}}}{{{\nu _{\text{w}}}}}$ 本研究使用REFPROP物性包,通过输入工况参数原始实验数据集获取相应工况下的流体物性,计算初始选择的无量纲数,构建超临界流体流动传热相关无量纲数数据集。
1.1.1 BPNN模型输入数据集划分及标准化
在机器学习实践中,特征向量中的不同特征往往具有不同的量纲和量纲单位,这样的情况会影响数据分析的结果。为消除特征之间的量纲影响,加快模型的求解速度和收敛速度,提高模型稳定性,采用Z-Score标准化处理数据集。转换函数如式(1)所示。
$$ x^{^{{\prime}}} = \frac{{x - \mu }}{\delta } $$ (1) 式中,x为样本;$ x^{^{{\prime}}} $为标准化后的样本;$ \mu $为数据集的均值;$ \delta $为数据集的标准差。
为防止测试集数据泄漏,影响模型泛化能力,应先划分数据集,再进行归一化处理。本研究将数据集打乱之后随机划分,其中80%的数据划分为训练集,20%的数据划分为测试集,在训练集上对模型的参数进行更新,在测试集上测试模型的泛化能力。对训练集进行标准化处理后,使用训练集上的均值和标准差对测试集进行标准化处理。
1.1.2 BPNN输入参数特征选择
由于所考虑的21个无量纲数数量较多,相互之间可能存在较强的相关性,为了剔除冗余特征、提高模型的准确度,采用Spearman相关系数法对原始特征集进行特征选择。
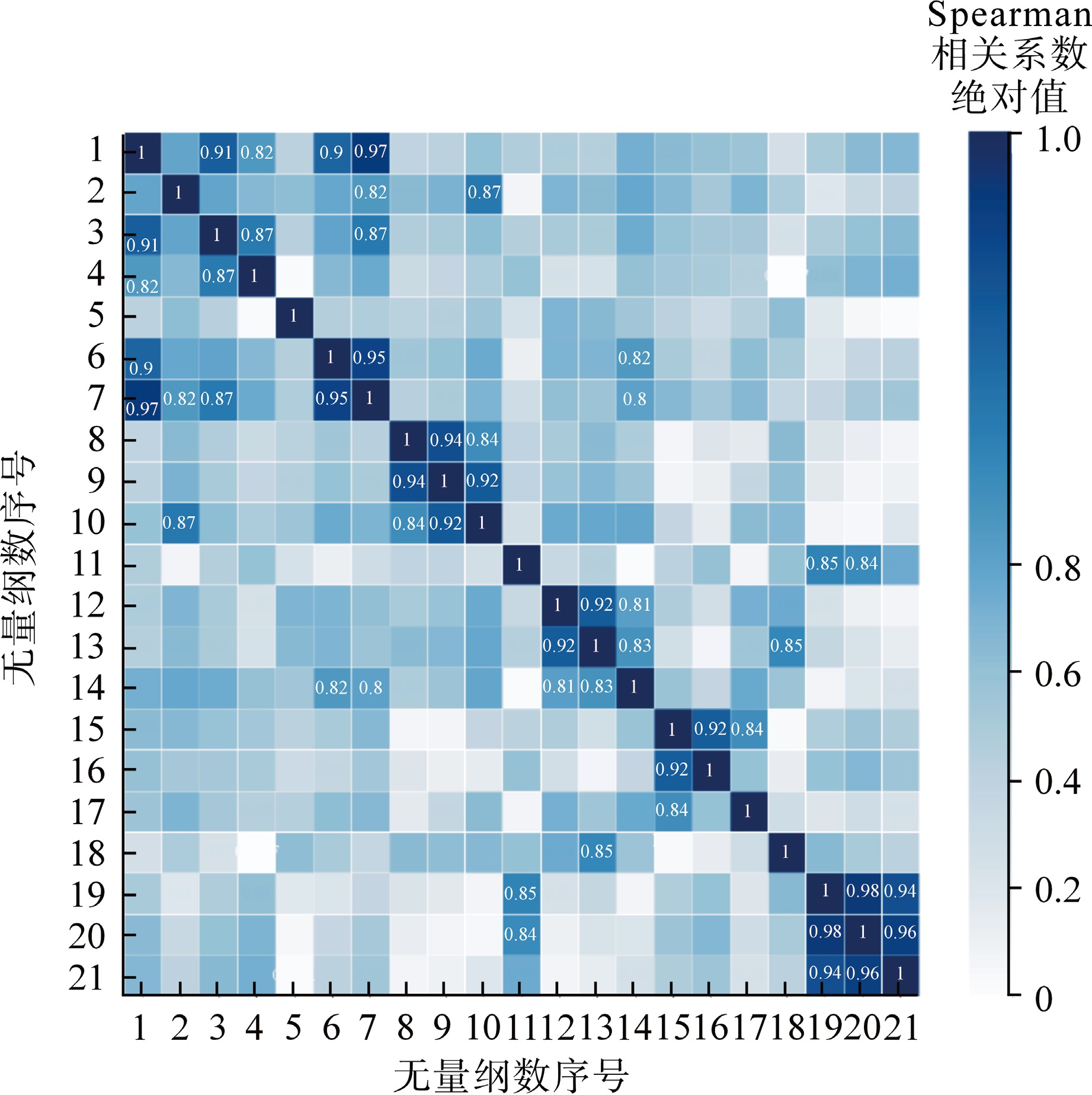
Spearman相关系数绝对值越接近1,表示两个特征之间存在的相关性越强。对于相关性强的特征对,两个特征具有相似的信息,因此可选用其中的一个。
因此,本研究特征选择的方法为:
(1)图2为Spearman相关系数绝对值矩阵,显示数值大于0.8的相关系数绝对值,基于图2选择出相关系数大于阈值0.8的特征对。
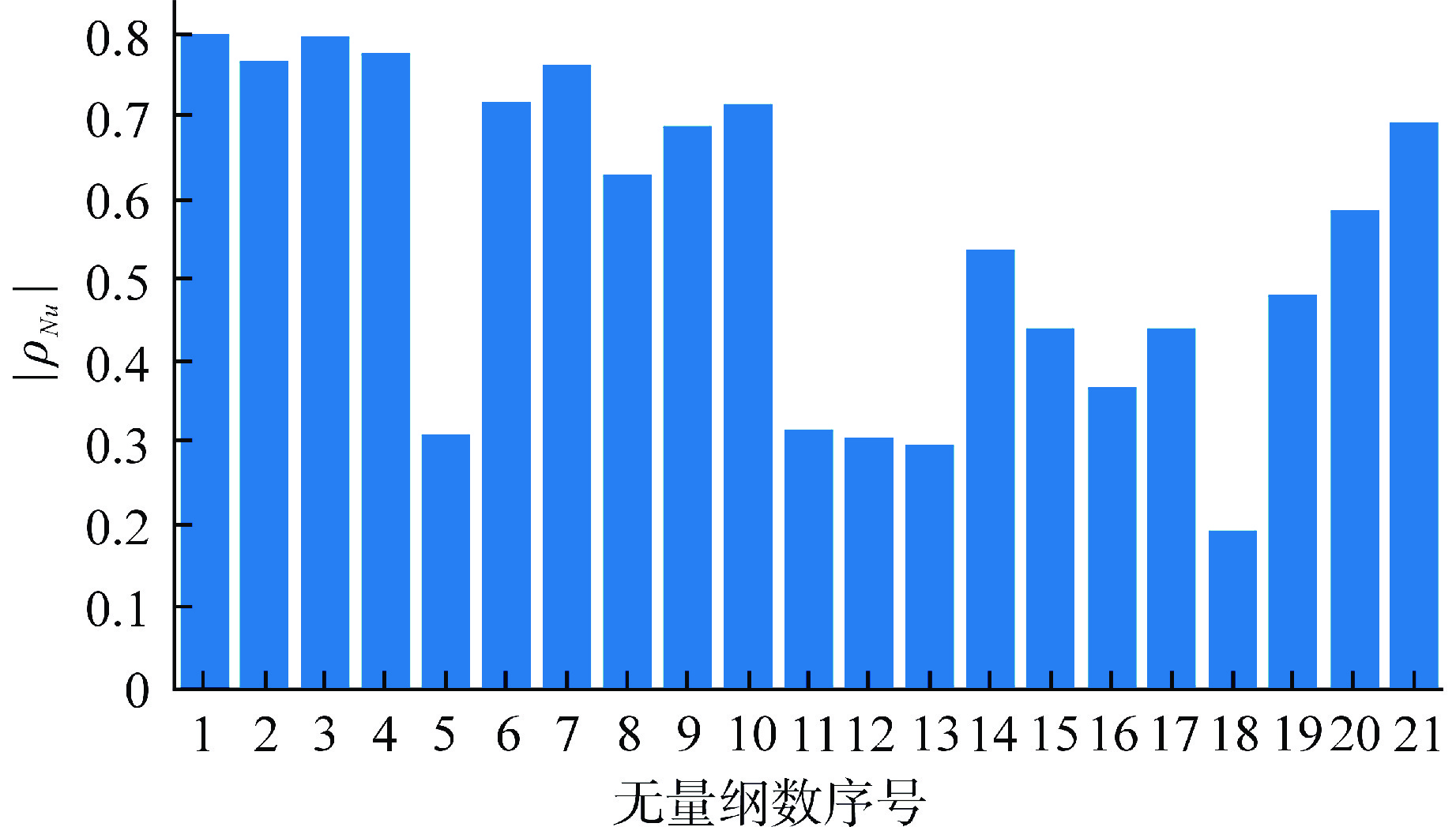
(2)根据图3,将特征对中两个特征与Nu的相关系数(ρNu)相比较,保留与Nu相关性较高的特征。
最终获得8个无量纲数:Reb、Prb、$ {\overline {Pr} _{\text{b}}} $、$ {{{\nu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\nu _{\text{b}}}} {{\nu _{\text{w}}}}}} \right. } {{\nu _{\text{w}}}}} $、$ {{{{\bar c}_p}} \mathord{\left/ {\vphantom {{{{\bar c}_p}} {{c_{p,{\text{w}}}}}}} \right. } {{c_{p,{\text{w}}}}}} $、$ {{{c_{p,{\text{b}}}}} \mathord{\left/ {\vphantom {{{c_{p,{\text{b}}}}} {{c_{p,{\text{pc}}}}}}} \right. } {{c_{p,{\text{pc}}}}}} $、Grb、Bu3。特征选择后的无量纲数数据集即为本文超临界传热预测模型BPNN的输入数据集。
1.2 超临界传热预测模型BPNN建立
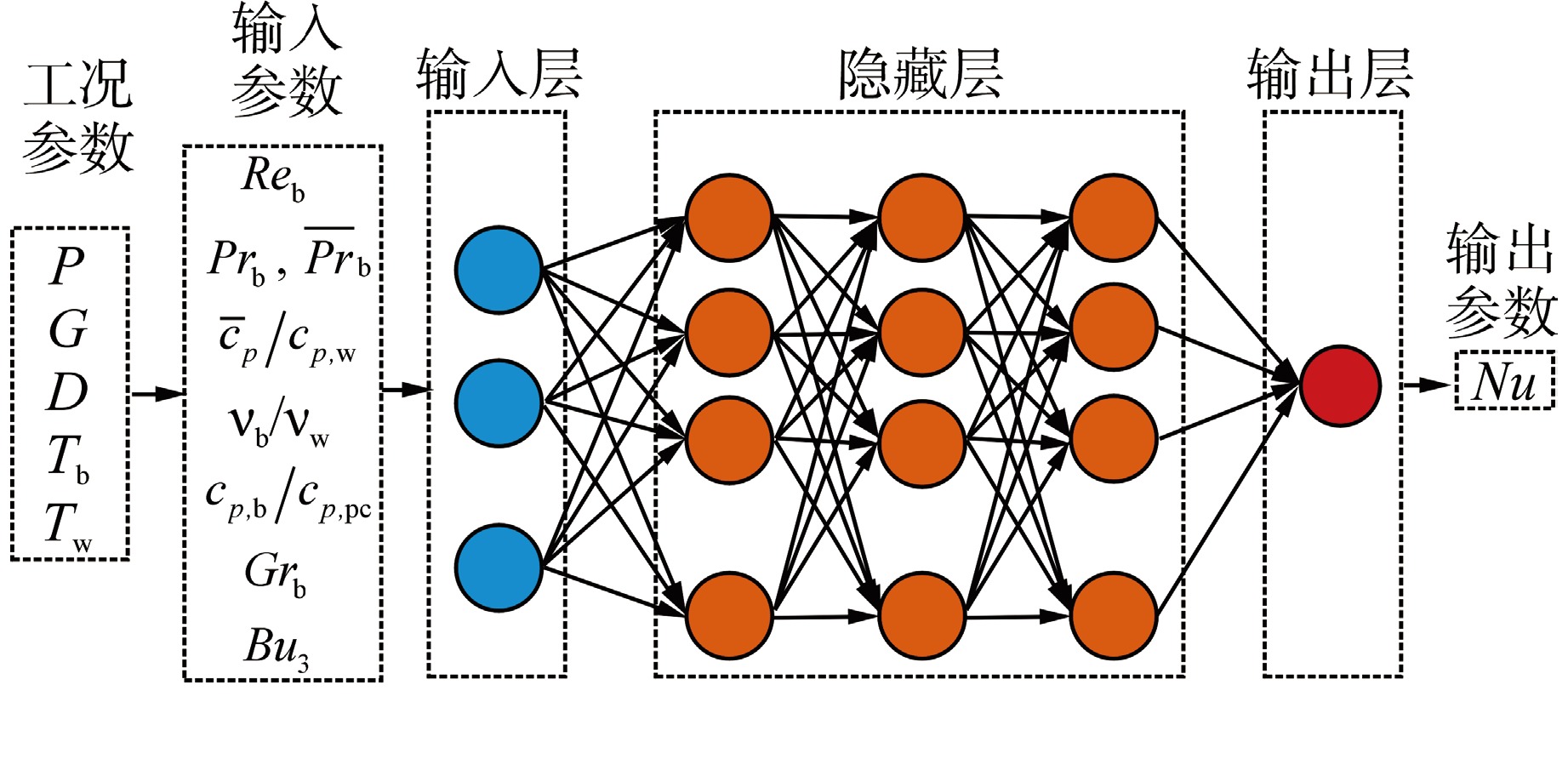
BPNN通常是指由误差反向传播算法训练的多层前馈网络,是应用最广泛的神经网络之一。本文使用PyTorch框架搭建BPNN作为超临界传热预测模型。BPNN模型构建包括PSO最优超参数搜索和模型构建,如图4所示。使用PSO搜索获得的超参数构建最优模型,结合测试集得到预测结果。
1.2.1 BPNN模型设置
模型结构如图4所示,BPNN模型包含一个输入层、若干隐藏层和一个输出层,每层包含多个神经元,每个神经元既有输入也有输出,一个神经元的输入来自前一层神经元的输出。输入层为1.1.2节中选择出的8个与超临界传热相关的无量纲数,输出层为包含传热系数的Nu。
权重和偏置初始化:在BPNN模型中,每个神经元具有相关的权重和偏置,这些权重和偏置是信号传递和激活过程中的关键参数,两者的调整和优化是模型训练的核心过程。权重初始化的目的是防止模型在前向传播过程中激活函数的输出损失梯度出现爆炸或消失,提高网络训练的效率和稳定性。而针对不同的激活函数,采用的初始化方法也不同。Kaiming初始化方法针对具有修正线性单元(ReLU)激活函数的网络模型[25],通过将权重初始化为从均值为0、方差为2/n的高斯分布中采样,其中n是上一层神经元的数量,从而解决梯度消失问题。对于偏置项不会存在梯度消失和爆炸问题,因此可以安全地将偏置初始化为0。因此,本文采用适用于ReLU激活函数的Kaiming初始化方法初始化模型权重,设置初始偏置为常数0。
模型参数更新:从输入样本开始,输入信号会经过每一层神经元权重和偏置的作用,并通过激活函数ReLU进行非线性的变换,通过网络的各层逐步传递信号,得到模型的预测值,之后通过均方误差(MSE)损失函数用于计算预测值和真实值之间的误差,并将该误差从输出层向隐藏层反向传播,使用梯度下降算法更新模型权重和偏置,从而最小化损失函数。本文使用Adam优化器更新网络参数。该算法是一种自适应学习率优化算法,可以根据每个参数的历史梯度信息来调整学习率,能够自动适应不同参数的更新速度。
1.2.2 BPNN模型最优超参数搜索
不同于训练过程中模型自行调整的权重和阈值,在训练开始之前,有一些超参数需要人为设定,这些超参数极大程度上决定了模型的性能。PSO算法具有良好的全局搜索能力,通过更新粒子的速度和位置,寻找目标函数的最优解,实现简单,收敛速度快且精度高。因此,本研究采用PSO算法对模型超参数进行寻优。
优化流程如图5所示。首先设置初始粒子群的位置,即粒子位置中每个超参数的初始值;计算每个粒子位置所对应的适应度函数的值,即使用每个粒子所代表的超参数组合训练模型,并将验证集上的损失作为适应度函数的值;根据粒子适应值更新单个粒子个体的最优值和全体粒子全局的最优值。接着更新粒子的速度和位置,继续计算粒子适应值,更新个体极值和全局极值直至达到终止迭代次数,最终输出搜索到的最优超参数组合。
为了使搜索到的超参数具有更好的泛化能力,防止过拟合,在最优超参数搜索过程中,本研究采用五折交叉验证,将训练集划分为5份,每份轮流作为验证集,评估超参数组合性能,其余4份作为训练集更新模型参数,之前划分的测试集不参与超参数的寻优过程。对于同一超参数组合,将获得5个模型的评估结果,得到的平均误差作为PSO算法的适应度函数,最小化适应度函数作为寻优方向。
1.3 超临界传热预测模型BPNN特征重要度分析
深度神经网络、支持向量机等机器学习模型具有较高的预测精度,但是可解释性较差,因此利用事后辅助的归因解析及可视化工具来提高模型的可解释性[26]。从模型解释的范围划分,模型解释分为全局解释和局部解释,全局解释是指理解模型在整个数据集上的预测行为,而局部解释是指分析模型在单个实例或数据子集上的预测行为[27]。SHAP可解释算法可以实现全局解释与局部解释,因此本文选用SHAP可解释算法对超临界传热预测模型BPNN进行特征重要度分析。
SHAP可解释算法以博弈论的思想,通过计算模型中各个特征的边际贡献来衡量各个特征的影响大小,进而对黑盒模型进行解释,该边际贡献被称为夏普利值。
边际贡献$ {\phi _i} $的计算公式为:
$$ \phi_i=\sum_{S \subseteq \left(M \backslash x_i\right)} \frac{|S|!(|M|-|S|-1)!}{|M|!} \Delta \psi $$ (2) $$ \Delta \psi=\left\{f\left(x_{S \cup(i)}\right)-f\left(x_S\right)\right\} $$ 式中,M为特征全集;S为除去$ {x_i} $的特征子集,$ S $的取值有多种情况,分别对应了不同的特征组合;$ f({x_{S \cup (i)}}) $和$ f({x_S}) $分别为各种特征组合下$ {x_i} $参与与不参与时的模型结果;$ \left|S\right|!(|M|-|S|-1)!/\left|M\right|! $表示各种参数组合对应的概率。式(2)表示在不同特征组合下,特征$ {x_i} $参与和$ {x_i} $不参与时的模型结果变化情况。
2. 结果与讨论
2.1 超临界传热预测模型BPNN最优超参数搜索结果
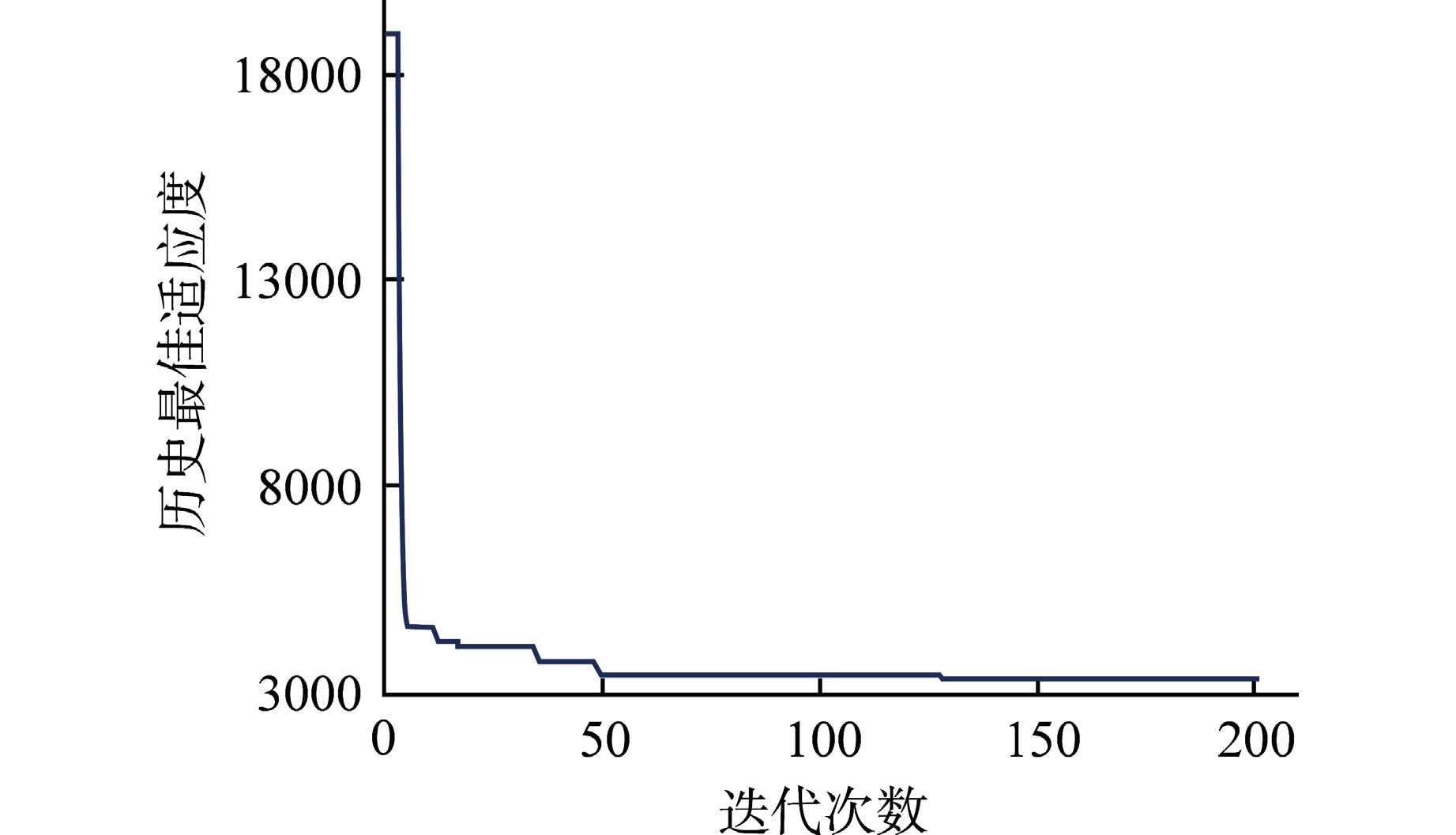
本研究采用PSO算法对超临界传热预测模型BPNN的隐藏层数、隐藏层节点数、初始学习率、批数量以及训练迭代次数进行搜索。如图6所示,历史最佳适应度随着优化迭代次数的增加呈现出明显的变化。在前50代的迭代中,适应度值发生较大的下降,在50代之后,适应度值变化较小,优化曲线逐渐收敛。当达到预设的200代优化迭代次数后,优化过程自动停止,并输出优化结果。超参数搜索空间与搜索结果如表2所示。
表 2 超参数搜索空间及搜索结果Table 2. Hyper Parameters Search Space and Results超参数名称 搜索范围 搜索结果 隐藏层数 1~4 2 隐藏层节点数 1~300 119、196 初始学习率 0.00009~0.009 3.0521×10−3 批数量 2~128 115 迭代次数 500~3000 2352 2.2 超临界传热预测模型BPNN预测结果
将搜索到的超参数组合代入模型,构建超临界传热预测模型BPNN。在之前划分的占比80%的训练集上进行模型参数的迭代更新,在占比20%的测试集上对模型进行精度与泛化能力的最终评估。
为评估超临界传热预测模型BPNN预测的性能,本研究以MAPE、RMSE、R2作为评判预测模型性能优劣的标准,各评估误差指标的计算公式如下:
$$ {\text{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left|\frac{{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }_i} - {y_i}}}{{{y_i}}}\right|} \times 100 \text{%} $$ (3) $$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }_i} - {y_i}} \right)}^2}} } $$ (4) $$ {R^2} = 1 - \frac{{\displaystyle\sum_{i = 1}^N {{{\left( {{y_i} - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} }_i}} \right)}^2}} }}{{\displaystyle\sum_{i = 1}^N {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} }} $$ (5) 式中,$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{y} _i} $为模型的预测值;$ {y_i} $为实验值;N为样本数。
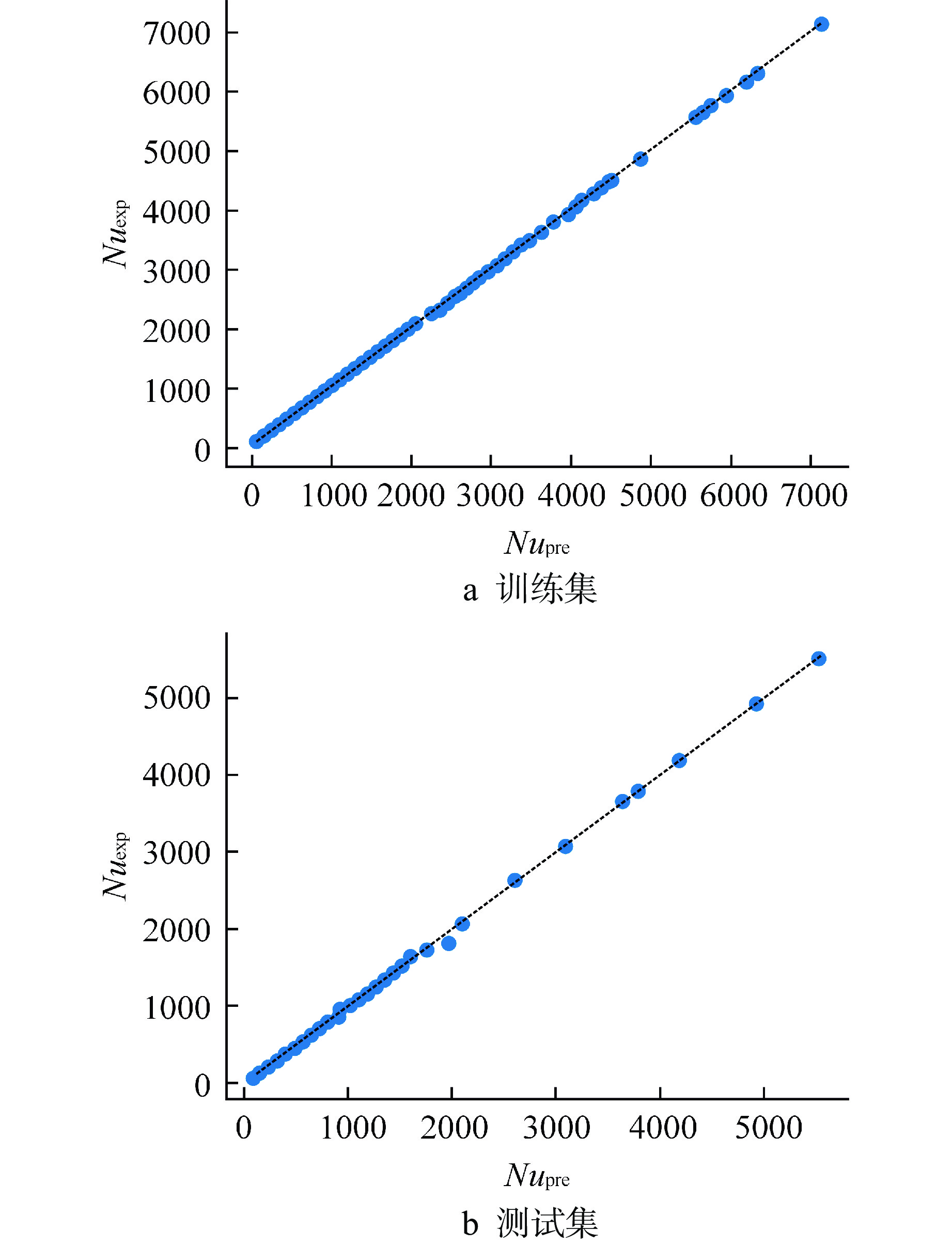
如图7所示,训练集和测试集上预测值与实验值基本呈现y=x分布,达到较好的拟合效果。根据训练集和测试集上不同预测误差对应的数据占比统计,如表3所示,测试集上95.31%的样本预测误差小于5%,训练集上98.74%的样本预测误差小于5%。
表 3 5%和10%预测误差对应数据占比Table 3. Proportion of Data Corresponding to the 5% and 10% Prediction Errors数据集 ${\eta _{5\text{%} }}$ ${\eta _{10\text{%} }}$ 训练集 98.74% 99.76% 测试集 95.31% 98.12% ${\eta _{5\text{%} }}$—预测误差小于5%的数据比例;${\eta _{10\text{%} }}$—预测误差小于5%的数据比例 从误差指标数值看,训练集和测试集的误差较为接近,MAPE分别为0.8%和1.4%,RMSE分别为7.0和18.8,测试集误差稍高于训练集,根据表4统计,测试集存在1.87%的样本(6个样本)预测误差较大,说明测试集中可能存在异常样本点,同时测试集数据点相对训练集较少,平衡异常误差的能力较弱,从而导致测试集上的MAPE、RMSE稍高。BPNN模型在训练集和测试集上的精度均较高,精度相差在合理的范围内,R2均在0.999左右,说明模型有效避免了过拟合,对Nu的预测达到了较高的精度。
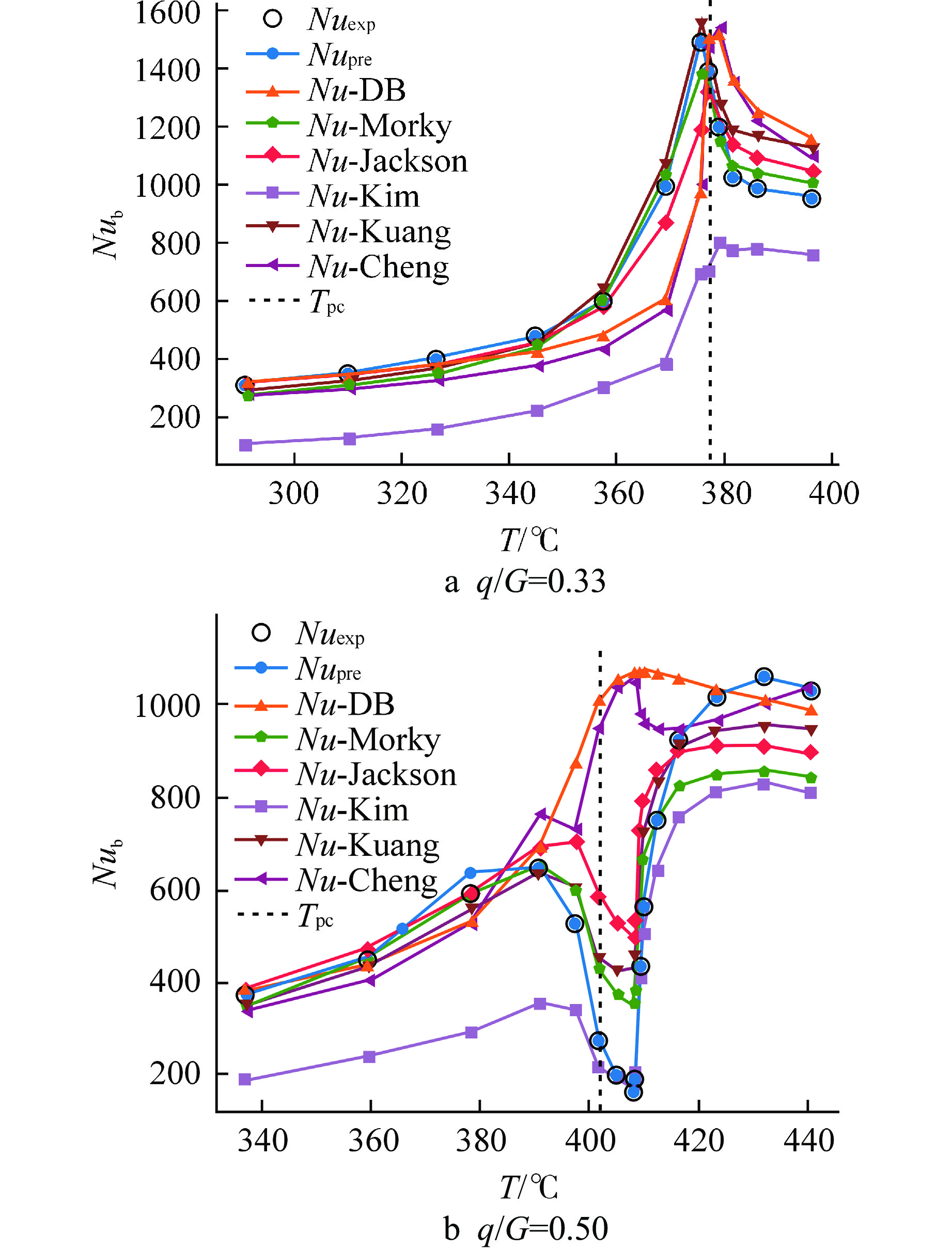
表 4 数据集误差Table 4. Dataset Error数据集 MAPE/% RMSE R2 训练集 0.8 7.0 0.99991 测试集 1.4 18.8 0.99921 使用6个现有经验关联式与BPNN模型在测试集上进行精度比对,结果如表5所示,BPNN模型预测结果的MAPE、RMSE、R2相对于其他关联式均具有显著的优势。选择q/G=0.33和q/G=0.50工况下关联式与BPNN的预测结果进行比对,如图8所示,在q/G=0.33工况下,各模型与实验数据均表现出相似的趋势,在q/G=0.50工况下,除去DB公式与Cheng关联式,其余关联式均预测出传热恶化的趋势,在两种工况下,本文所提出的超临界传热预测模型BPNN预测结果与实验结果最为接近。
表 5 BPNN与现有关联式比对结果Table 5. Comparison Results between BPNN and Existing Correlations选择支持向量机回归模型(SVR)和随机森林回归模型(RFR)与本研究提出的BPNN模型在测试集上进行对比,对比结果如表6所示。由于本研究建立的BPNN模型每层具有较多的神经元,从而导致该模型的训练过程涉及到大量参数的矩阵和激活函数的运算,而SVR和RFR具有更简单的模型结构,因此BPNN模型在计算速度上慢于另外两个模型,但是BPNN模型能够学习到更复杂的特征,在3个指标上均体现出更高的精度优势。
表 6 不同模型的对比结果Table 6. Comparison of Different Models模型 训练时间/s MAPE/% RMSE R2 SVR 13.46 3.9 50.9 0.994 RFR 24.63 3.5 82.3 0.984 BPNN 129.01 1.4 18.8 0.999 2.3 超临界传热预测模型BPNN特征重要度分析结果
2.2节的评估结果说明本文提出的超临界传热预测模型BPNN具有较高的精度和较好的泛化性能,因此可认为BPNN模型已经较好地学习到数据的规律,捕获了数据中蕴含的输入变量与目标变量之间的内在关系。因此可采用SHAP可解释算法对BPNN模型在全部数据集以及局部数据子集上的预测行为分别进行全局解释和局部解释,并基于具有物理意义的特征的特征重要度发掘超临界相关机理。
为更清晰地比对特征重要度的变化,对每个样本中特征的夏普利值的绝对值进行归一化。在SHAP特征重要度图中,横轴为每个特征夏普利值绝对值的平均值,该值越大,则说明在所选工况下,该特征对BPNN模型预测越重要,即对目标参数影响越大。
2.3.1 超临界传热预测模型BPNN全局特征重要度分析结果
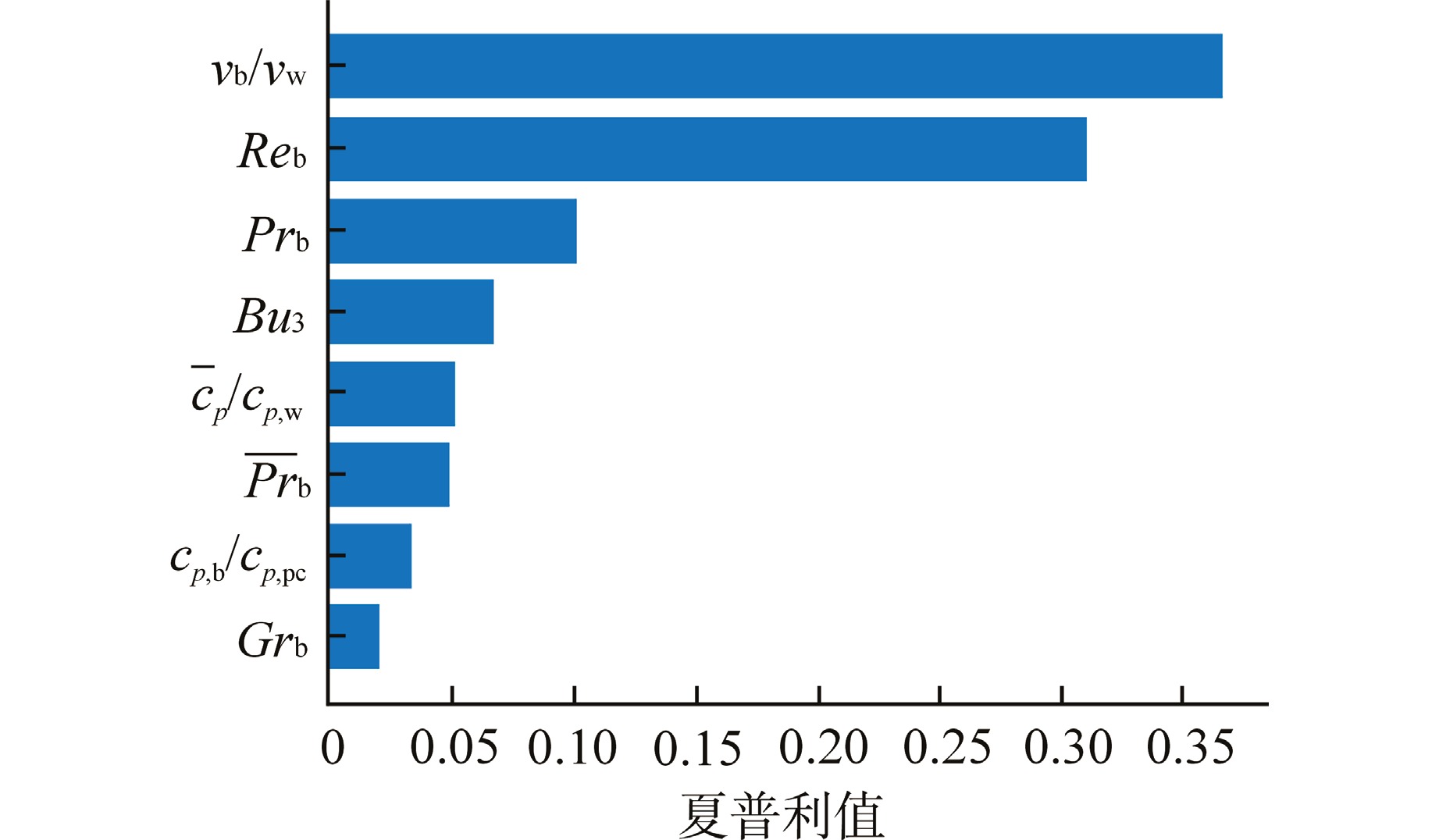
通过全局解释,获得在所有工况条件下所有样本每个特征的特征重要度绝对值的平均值,从而获得在整个实验数据范围内起重要作用的特征。全局解释结果如图9所示,在所有工况范围内,$ {\nu }_{\text{b}}/{\nu }_{\text{w}}、R{e}_{\text{b}}、P{r}_{\text{b}} $的重要度最高,说明对于超临界流体的换热,径向物性的修正对于Nu的预测起到十分重要的作用。
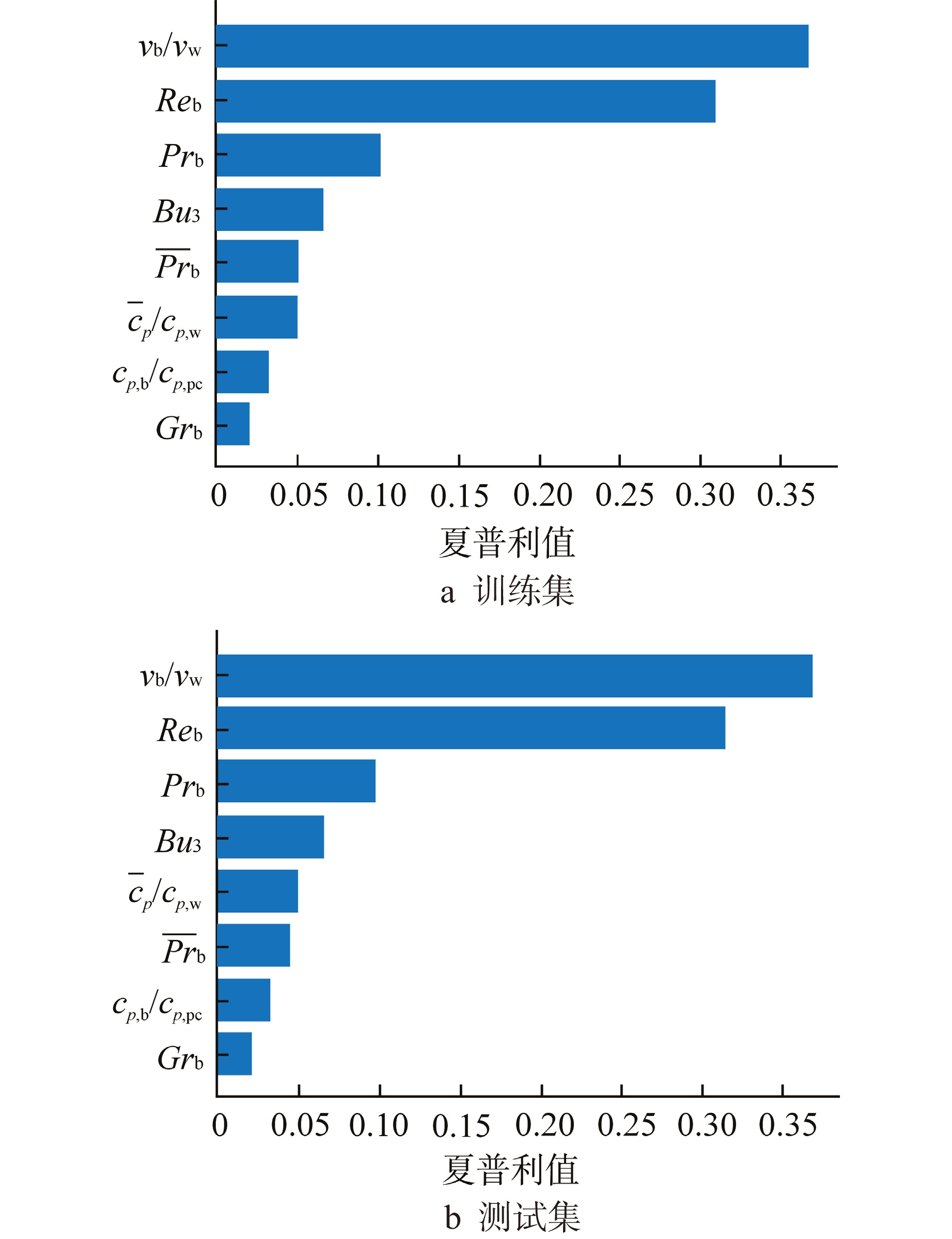
由于测试集包含与训练集不同的样本,它可以提供对BPNN模型在新数据上的解释能力的评估。因此训练集和测试集上解释结果是否一致和稳定,也可以用于评估模型的可靠性和泛化能力。如图10所示,通过全局解释结果和训练集、测试集解释结果比对,特征重要度排序稳定,在重要度较低的${\bar c_p}/{c_{p,{\text{w}}}}$、${\overline {Pr} _{\text{b}}}$处排序稍有变化,在重要度较高的特征,其排序均未发生变化,因此说明BPNN模型解释结果比较稳定,具有较好的泛化能力。
2.3.2 超临界传热模型在传热强化及恶化工况处特征重要度分析结果
为研究不同工况下的超临界传热机理,对BPNN模型在发生传热恶化和传热强化的两组工况下的预测行为进行特征重要度分析。
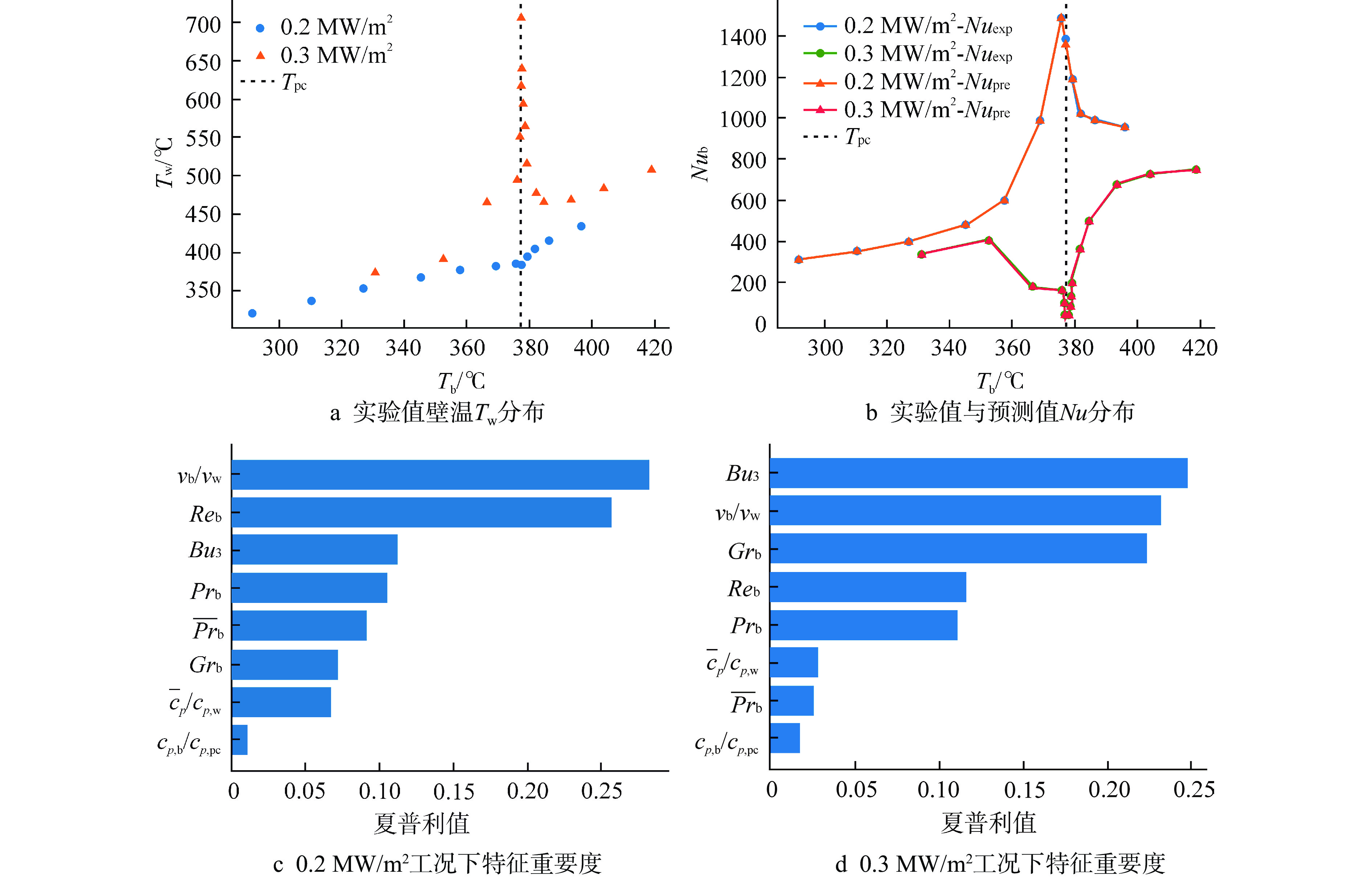
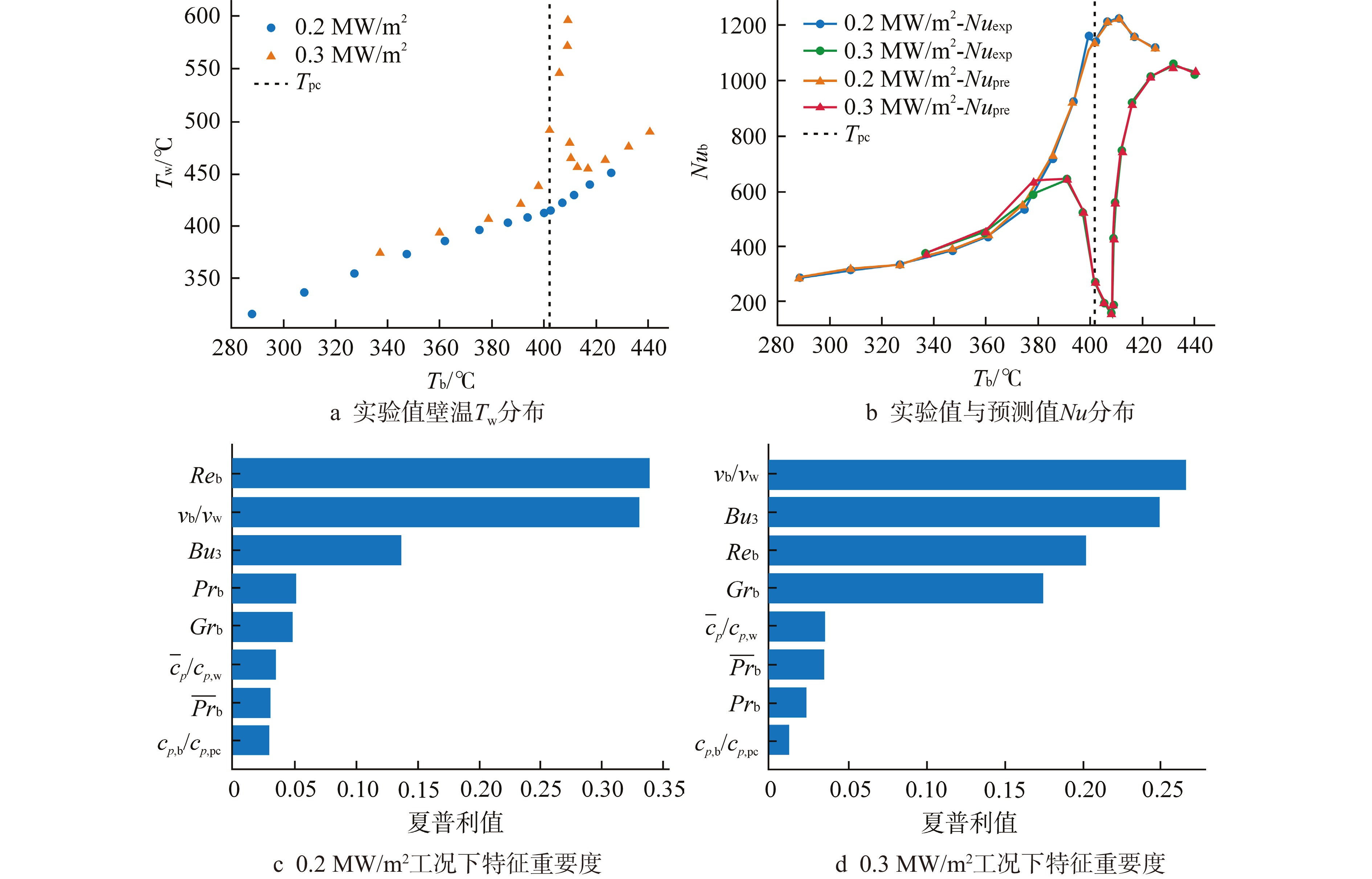
选择的2组工况分别为:①工况1:管径26 mm,压力23 MPa,质量流量600 kg/(m2·s)条件下,热流密度从0.2 MW/m2增加到0.3 MW/m2;②工况2:管径26 mm,压力30 MPa,质量流量600 kg/(m2·s)条件下,热流密度从0.2 MW/m2增加到0.3 MW/m2。如图11a和图11b所示,在0.2 MW/m2热流密度下,Nu分布曲线在拟临界温度附近有明显峰值,而Tw分布曲线在拟临界温度处趋势变缓,此时为传热强化行为。而随着热流密度的增加,0.3 MW/m2热流密度下,Nu分布曲线在拟临界温度附近急剧下降,Tw分布曲线在拟临界温度附近有明显飞升,此时发生明显的传热恶化。如图11b和图12b所示,对于发生传热强化或传热恶化的工况,本文所提出的超临界流体传热预测模型BPNN均可以做出准确的预测。
对BPNN模型在两组工况下的预测行为分别做局部解释,获得的特征重要度变化如图11c、图11d和图12c、图12d所示。在两组工况下,热流密度从0.2 MW/m2增加到0.3 MW/m2,传热行为由传热强化转变为传热恶化。图11c和图12c对应工况发生传热强化,$R{e_{\text{b}}}$和${\nu _{\text{b}}}/{\nu _{\text{w}}}$相对其他特征具有显著的特征重要度。图11d和图12d对应工况发生传热恶化,$ B{u}_{3}、{\nu }_{\text{b}}/{\nu }_{\text{w}} $、$G{r_{\text{b}}}$相对其他特征具有显著的特征重要度。局部解释的结果说明在两种传热行为中,代表径向物性不均匀性的${\nu _{\text{b}}}/{\nu _{\text{w}}}$对Nu的预测起到较为重要的作用,在传热强化工况中,代表湍流强度的$ Re_{\mathrm{b}} $对传热起到十分重要的作用,而浮升力效应对应的$B{u_3}$和$G{r_{\text{b}}}$在传热恶化工况中明显具有更高的特征重要度,对Nu的影响更大。
3. 结 论
本研究采用可解释机器的研究方法,离线阶段采用PSO算法搜索最优超参数,搭建超临界传热预测模型BPNN,在线阶段使用超临界水在垂直上升管中流动传热实验数据训练并评估BPNN模型,最后对BPNN模型进行全局解释与局部解释,以预测模型为媒介,发现超临界相关机理现象,获得如下结论:
(1)本研究建立的超临界传热预测模型BPNN预测精度明显优于经验关联式和SVR、RFR等黑盒模型,在测试集上的MAPE达到1.4%,R2达到0.9992。
(2)全局特征重要度分析比对结果验证了该BPNN模型具有较好的泛化性能且解释结果具有稳定性,发现对于超临界流体的换热,径向物性的修正对于Nu的预测起到十分重要的作用。不同工况下的局部解释发现在传热强化工况中,$R{e_b}$对传热起重要作用,而表征浮升力效应的特征$B{u_3}$和$G{r_{\text{b}}}$在传热恶化工况下具有更高的特征重要度,说明浮升力效应是传热恶化行为发生的主要因素。
参数符号表:
${c_p}$:定压比热容,J/(kg·K)
${\bar c_p}$:平均定压比热容,J/(kg·K)
d:管内径,mm
g:重力加速度,9.81 m/s2
G:质量流量,kg/(m2·s)
h:传热系数,W/(m2·K)
$k$:导热系数,W/(m·K)
P:压力,bar(1 bar=105 Pa)
q:热流密度,kW/m2
T:温度,℃
u:流动速度,m/s
$\eta $:一定误差范围内的数据比例
$\rho $:密度,kg/m3
$\mu $:动力粘度,kg/(m·s)
$\upsilon $:运动粘度,m2/s
$Re$:雷诺数
$Pr$:普朗特数
$\overline {Pr} $:平均普朗特数
$G{r_{\text{b}}}$:格拉晓夫数
$ Bu_{ } $:浮升力因子
Nu:努塞尔数
下标
b:流体
w:壁面
f:平均
pc:拟临界
pre:预测
exp:实验
-
表 1 特征选择前的无量纲数
Table 1. Dimensionless Number before Feature Selection
序号 无量纲数 序号 无量纲数 1 $R{e_{\text{b}}}$ 12 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{w}}}}}}$ 2 $P{r_{\text{b}}}$ 13 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{b}}}}}}$ 3 $R{e_{\text{w}}}$ 14 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{w}}}}}}$ 4 $R{e_{\text{f}}}$ 15 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{{\text{pc}}}}}}$ 5 $P{r_{\text{w}}}$ 16 $\dfrac{{{k_{\text{b}}}}}{{{k_{{\text{pc}}}}}}$ 6 ${\overline {Pr} _{\text{b}}}$ 17 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{pc}}}}}}$ 7 ${\overline {Pr} _{\text{w}}}$ 18 $ Gr_{\text{b}}=\dfrac{\left(\rho_{\text{b}}-\rho_{\text{w}}\right)gd^3}{\rho_{\text{b}}\mathit{\upsilon}_{\text{b}}^2} $ 8 $\dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{w}}}}}$ 19 $B{u_1} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^2}}$ 9 $\dfrac{{{k_{\text{b}}}}}{{{k_{\text{w}}}}}$ 20 $B{u_2} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.7}}}$ 10 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}$ 21 $B{u_3} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.625}Pr_{\text{w}}^{{\text{0}}{\text{.4}}}}}{\left( {\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\text{w}}}}}{{{\mu _{\text{b}}}}}} \right)$ 11 $\dfrac{{{\nu _{\text{b}}}}}{{{\nu _{\text{w}}}}}$ 表 2 超参数搜索空间及搜索结果
Table 2. Hyper Parameters Search Space and Results
超参数名称 搜索范围 搜索结果 隐藏层数 1~4 2 隐藏层节点数 1~300 119、196 初始学习率 0.00009~0.009 3.0521×10−3 批数量 2~128 115 迭代次数 500~3000 2352 表 3 5%和10%预测误差对应数据占比
Table 3. Proportion of Data Corresponding to the 5% and 10% Prediction Errors
数据集 ${\eta _{5\text{%} }}$ ${\eta _{10\text{%} }}$ 训练集 98.74% 99.76% 测试集 95.31% 98.12% ${\eta _{5\text{%} }}$—预测误差小于5%的数据比例;${\eta _{10\text{%} }}$—预测误差小于5%的数据比例 表 4 数据集误差
Table 4. Dataset Error
数据集 MAPE/% RMSE R2 训练集 0.8 7.0 0.99991 测试集 1.4 18.8 0.99921 表 5 BPNN与现有关联式比对结果
Table 5. Comparison Results between BPNN and Existing Correlations
表 6 不同模型的对比结果
Table 6. Comparison of Different Models
模型 训练时间/s MAPE/% RMSE R2 SVR 13.46 3.9 50.9 0.994 RFR 24.63 3.5 82.3 0.984 BPNN 129.01 1.4 18.8 0.999 -
[1] XIE G N, XU X X, LEI X L, et al. Heat transfer behaviors of some supercritical fluids: a review[J]. Chinese Journal of Aeronautics, 2022, 35(1): 290-306. doi: 10.1016/j.cja.2020.12.022 [2] SWENSON H S, CARVER J R, KAKARALA C R. Heat transfer to supercritical water in smooth-bore tubes[J]. Journal of Heat Transfer, 1965, 87(4): 477-483. doi: 10.1115/1.3689139 [3] PETUKHOV B S. Heat transfer and friction in turbulent pipe flow with variable physical properties[J]. Advances in Heat Transfer, 1970, 6: 503-564. [4] KIM J K, JEON H K, LEE J S. Wall temperature measurement and heat transfer correlation of turbulent supercritical carbon dioxide flow in vertical circular/non-circular tubes[J]. Nuclear Engineering and Design, 2007, 237(15-17): 1795-1802. doi: 10.1016/j.nucengdes.2007.02.017 [5] JACKSON J D. An semi-empirical model of turbulent convective heat transfer to fluids at supercritical pressure[C]//Proceedings of the 16th International Conference on Nuclear Engineering. Orlando: ASME, 2008: 911-921. [6] FANG X D, XU Y. Modified heat transfer equation for in-tube supercritical CO2 cooling[J]. Applied Thermal Engineering, 2011, 31(14-15): 3036-3042. doi: 10.1016/j.applthermaleng.2011.05.037 [7] CHENG X, ZHAO M, FEUERSTEIN F, et al. Prediction of heat transfer to supercritical water at different boundary conditions[J]. International Journal of Heat and Mass Transfer, 2019, 131: 527-536. doi: 10.1016/j.ijheatmasstransfer.2018.11.028 [8] LI Y, CHEN Y Q, ZHANG Y C, et al. An improved heat transfer correlation for supercritical aviation kerosene flowing upward and downward in vertical tubes[J]. Journal of Thermal Science, 2020, 29(1): 131-143. doi: 10.1007/s11630-019-1197-2 [9] CHENG X, KUANG B, YANG Y H. Numerical analysis of heat transfer in supercritical water cooled flow channels[J]. Nuclear Engineering and Design, 2007, 237(3): 240-252. doi: 10.1016/j.nucengdes.2006.06.011 [10] ZHANG B, SHAN J Q, JIANG J. Numerical analysis of supercritical water heat transfer in horizontal circular tube[C]//Proceedings of the 17th International Conference on Nuclear Engineering. Brussels: ICONE, 2009: 471-479. [11] PANDEY S, LAURIEN E, CHU X. A modified convective heat transfer model for heated pipe flow of supercritical carbon dioxide[J]. International Journal of Thermal Sciences, 2017, 117: 227-238. doi: 10.1016/j.ijthermalsci.2017.03.021 [12] ZVORYKIN A, FIALKO N, JULII S, et al. CFD study on specifics of flow and heat transfer in vertical bare tubes cooled with water at supercritical pressures[C]//Proceedings of the 25th International Conference on Nuclear Engineering, Shanghai: AS ME, 2017: V009T15A013. [13] XU K K, RUAN B, MENG H. Validation and analyses of RANS CFD models for turbulent heat transfer of hydrocarbon fuels at supercritical pressures[J]. International Journal of Thermal Sciences, 2018, 124: 212-226. doi: 10.1016/j.ijthermalsci.2017.10.019 [14] YANG Z, CHENG X, ZHENG X H, et al. Reynolds-averaged Navier-Stokes equations describing turbulent flow and heat transfer behavior for supercritical fluid[J]. Journal of Thermal Science, 2021, 30(1): 191-200. doi: 10.1007/s11630-020-1339-6 [15] LIU X J, SONG M Q, CHENG X. Current status and challenges of supercritical fluid thermal hydraulics[J]. Nuclear Engineering and Design, 2019, 354: 110176. doi: 10.1016/j.nucengdes.2019.110176 [16] ZHANG R Z, TONG W T, XU S Y, et al. ANN model with feature selection to predict turbulent heat transfer characteristics of supercritical fluids: take CO2 and H2O as examples[J]. International Journal of Thermal Sciences, 2023, 188: 108247. doi: 10.1016/j.ijthermalsci.2023.108247 [17] AMARDEEP S, SALIGRAM A K, KASHYAP S R, et al. Heat transfer characteristics for upward flow of supercritical water in a vertical pipe–computational fluid dynamics analysis and artificial neural network prediction[J]. International Journal of Thermal Sciences, 2023, 184: 107990. doi: 10.1016/j.ijthermalsci.2022.107990 [18] MA D L, ZHOU T, CHEN J, et al. Supercritical water heat transfer coefficient prediction analysis based on BP neural network[J]. Nuclear Engineering and Design, 2017, 320: 400-408. doi: 10.1016/j.nucengdes.2017.06.013 [19] SUN F, XIE G N, LI S L. An artificial-neural-network based prediction of heat transfer behaviors for in-tube supercritical CO2 flow[J]. Applied Soft Computing, 2021, 102: 107110. doi: 10.1016/j.asoc.2021.107110 [20] PESTEEI S M, MEHRABI M. Modeling of convection heat transfer of supercritical carbon dioxide in a vertical tube at low Reynolds numbers using artificial neural network[J]. International Communications in Heat and Mass Transfer, 2010, 37(7): 901-906. doi: 10.1016/j.icheatmasstransfer.2010.05.018 [21] GUIDOTTI R, MONREALE A, RUGGIERI S, et al. A survey of methods for explaining black box models[J]. ACM Computing Surveys (CSUR), 2018, 51(5): 93. [22] Hall W B, Jackson J D, Watson A. Paper 3: A review of forced convection heat transfer to fluids at supercritical pressures[C]//Proceedings of the institution of mechanical engineers, conference proceedings. Sage UK: London, England: SAGE Publications, 1967, 182(9): 10-22. [23] JIANG P X, ZHANG Y, ZHAO C R, et al. Convection heat transfer of CO2 at supercritical pressures in a vertical mini tube at relatively low Reynolds numbers[J]. Experimental Thermal and Fluid Science, 2008, 32(8): 1628-1637. doi: 10.1016/j.expthermflusci.2008.05.006 [24] LIU S H, HUANG Y P, LIU G X, et al. Improvement of buoyancy and acceleration parameters for forced and mixed convective heat transfer to supercritical fluids flowing in vertical tubes[J]. International Journal of Heat and Mass Transfer, 2017, 106: 1144-1156. doi: 10.1016/j.ijheatmasstransfer.2016.10.093 [25] HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: surpassing human-level performance on imagenet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 1026-1034. [26] CARVALHO D V, PEREIRA E M, CARDOSO J S. Machine learning interpretability: A survey on methods and metrics[J]. Electronics, 2019, 8(8): 832. doi: 10.3390/electronics8080832 [27] SUDJIANTO A, ZHANG A. Designing inherently interpretable machine learning models[J]. 2021. DOI: 10.48550/arXiv.2111.01743. [28] DITTUS F W, BOELTER L M K. Heat transfer in automobile radiators of the tubular type[J]. International Communications in Heat and Mass Transfer, 1985, 12(1): 3-22. doi: 10.1016/0735-1933(85)90003-X [29] MOKRY S, PIORO I, FARAH A, et al. Development of supercritical water heat-transfer correlation for vertical bare tubes[J]. Nuclear Engineering and Design, 2011, 241(4): 1126-1136. doi: 10.1016/j.nucengdes.2010.06.012 [30] JACKSON J D. Fluid flow and convective heat transfer to fluids at supercritical pressure[J]. Nuclear Engineering and Design, 2013, 264: 24-40. doi: 10.1016/j.nucengdes.2012.09.040 [31] CHENG X, YANG Y H, HUANG S F. A simplified method for heat transfer prediction of supercritical fluids in circular tubes[J]. Annals of Nuclear Energy, 2009, 36(8): 1120-1128. doi: 10.1016/j.anucene.2009.04.016 [32] XIN L, BO K. Wide-ranged heat transfer correlations of supercritical water in vertical upward channels[J]. Nuclear Science & Engineering, 2012, 32(4): 344-353. [33] KIM D E, KIM M H. Experimental investigation of heat transfer in vertical upward and downward supercritical CO2 flow in a circular tube[J]. International Journal of Heat and Fluid Flow, 2011, 32(1): 176-191. doi: 10.1016/j.ijheatfluidflow.2010.09.001 -







 下载:
下载:











 下载:
下载: