Prediction and Analysis of Heat Transfer Characteristics of Supercritical Fluids Based on Interpretable Machine Learning
-
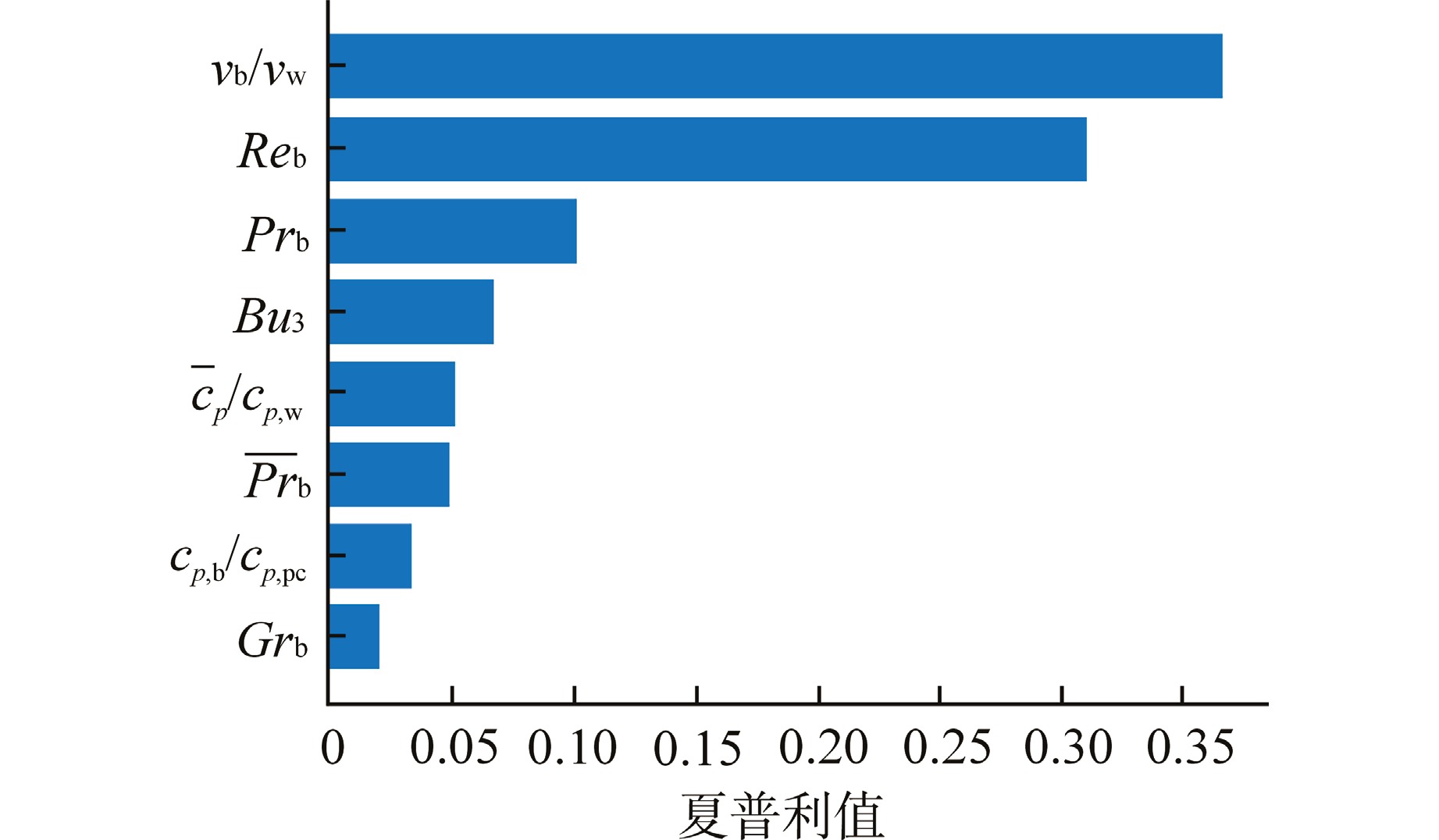
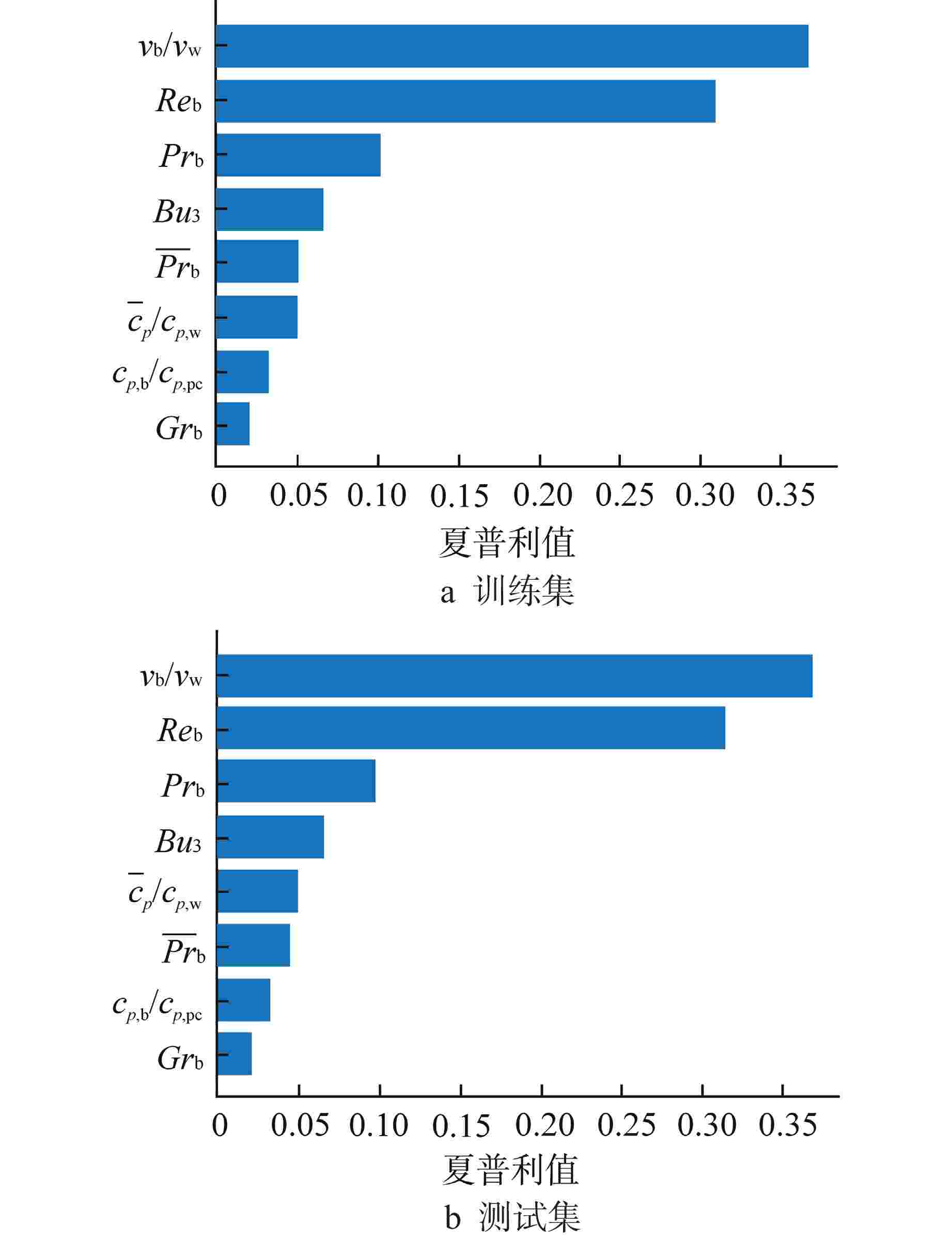
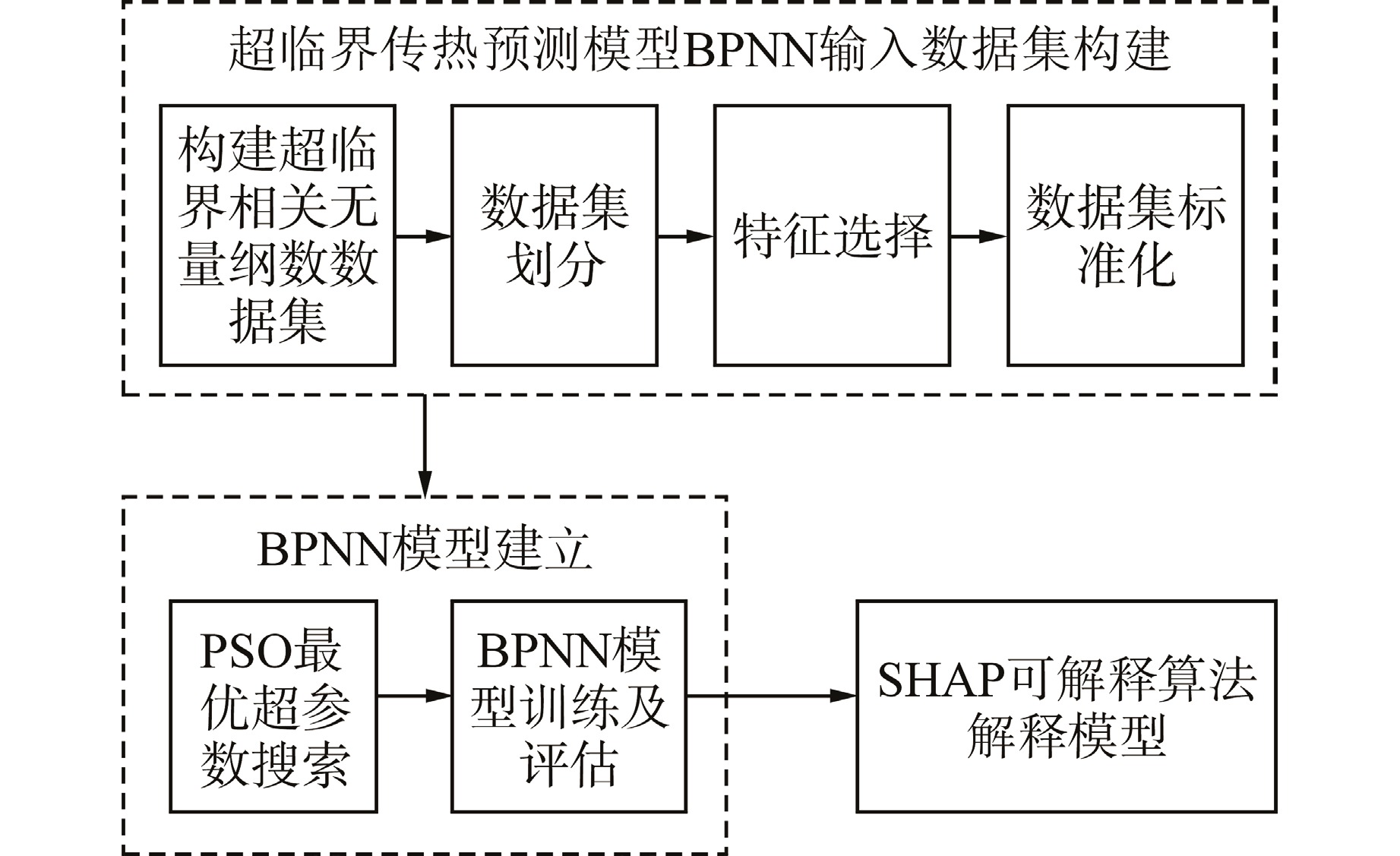
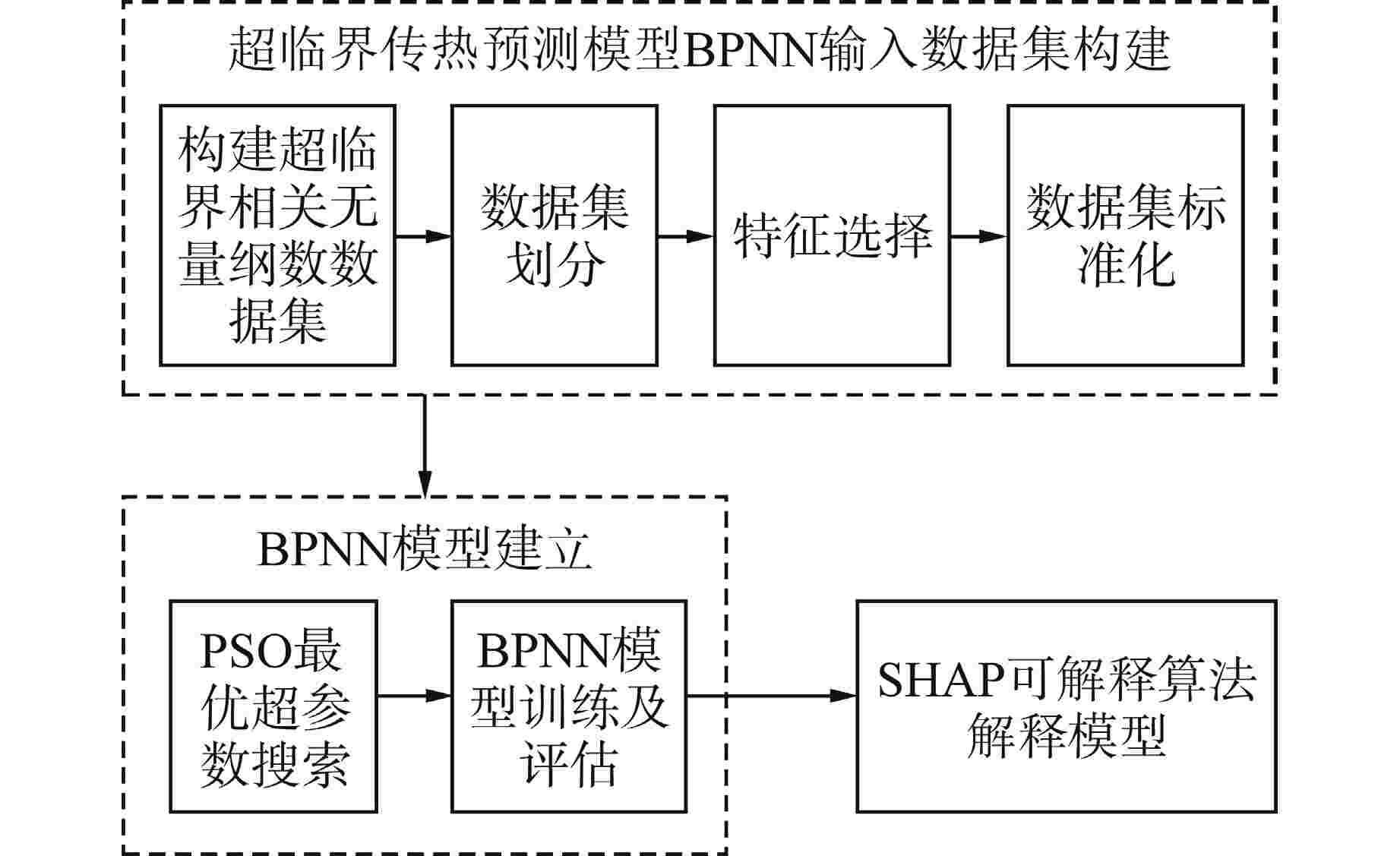
摘要: 超临界流体在拟临界温度附近发生剧烈的物性变化,传热特性难以准确预测。本研究采用可解释机器学习的研究方法预测并分析超临界流体传热特性。使用粒子群优化算法(PSO)搜索反向传播神经网络(BPNN)模型最优超参数,建立了超临界流体传热预测模型,并与传统经验关联式进行了精度比较。使用SHAP可解释算法对BPNN模型进行了全局和局部解释,根据不同工况下特征重要度的变化发现超临界相关机理现象。结果显示,所建立的神经网络模型在测试集上的平均绝对百分比误差(MAPE)为1.4%,决定系数R2为0.9992,与经验关联式相比,该模型具有更高的预测精度;对于垂直向上流动,浮升力效应在传热恶化工况中明显具有更高的特征重要度,是传热恶化行为发生的主要因素。因此,本研究建立的基于可解释机器学习的研究方法对进一步研究超临界流体传热特性具有一定的参考意义。Abstract: The physical properties of supercritical fluids change drastically near the pseudo-critical temperature, making it challenging to accurately predict heat transfer characteristics. In this study, the method of interpretable machine learning was used to predict and analyze the heat transfer characteristics of supercritical fluids. The particle swarm optimization algorithm (PSO) was used to search for the optimal hyperparameters of the back propagation neural network (BPNN) model, the supercritical fluid heat transfer prediction model was established, and its accuracy was compared with the traditional empirical correlation. The global and local interpretation of the BPNN model was carried out by using the SHAP interpretable algorithm, and the supercritical correlation phenomenon and mechanism were found according to the change of feature importance under different conditions. The results show that the MAPE of the established neural network model on the test set is 1.4%, and the coefficient of determination R2 is 0.9992, which has higher prediction accuracy compared with the empirical correlation formula. For vertical upward flow, buoyancy effect obviously has higher feature importance in heat transfer deterioration condition, which is the main factor of heat transfer deterioration behavior. Therefore, the research method based on interpretable machine learning established in this study has certain reference significance for further study of the heat transfer characteristics of supercritical fluids.
-
表 1 特征选择前的无量纲数
Table 1. Dimensionless Number before Feature Selection
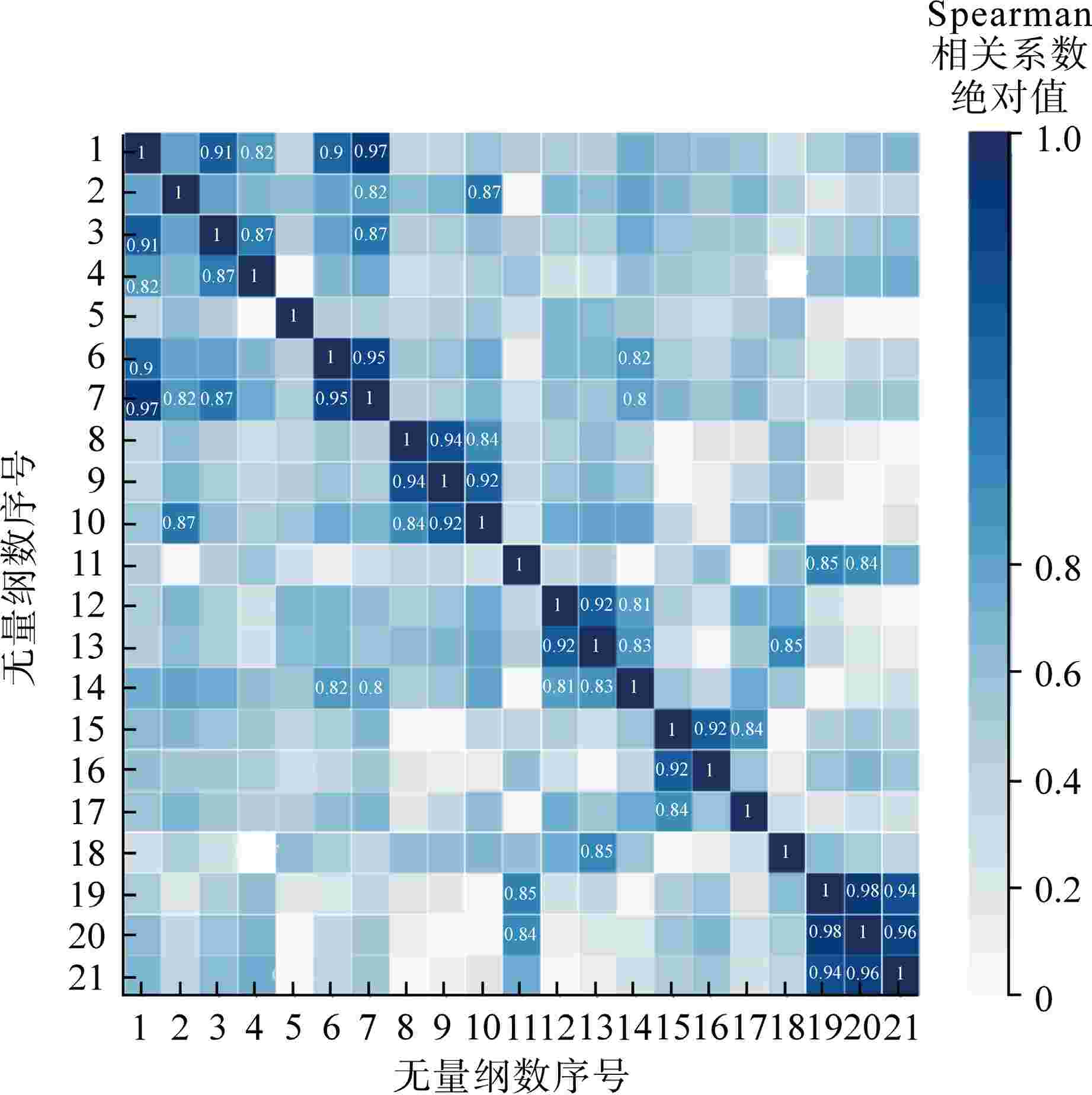
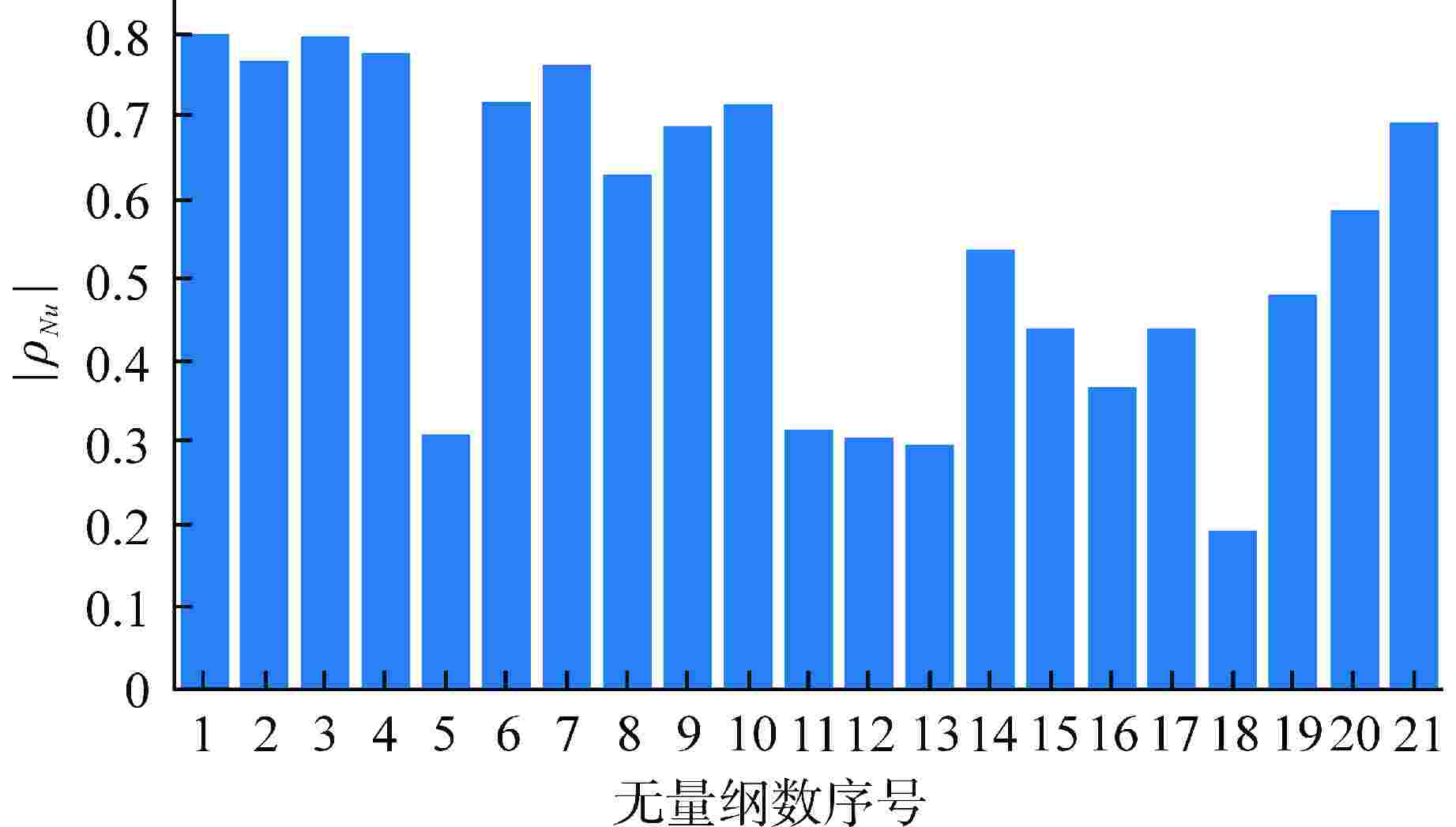
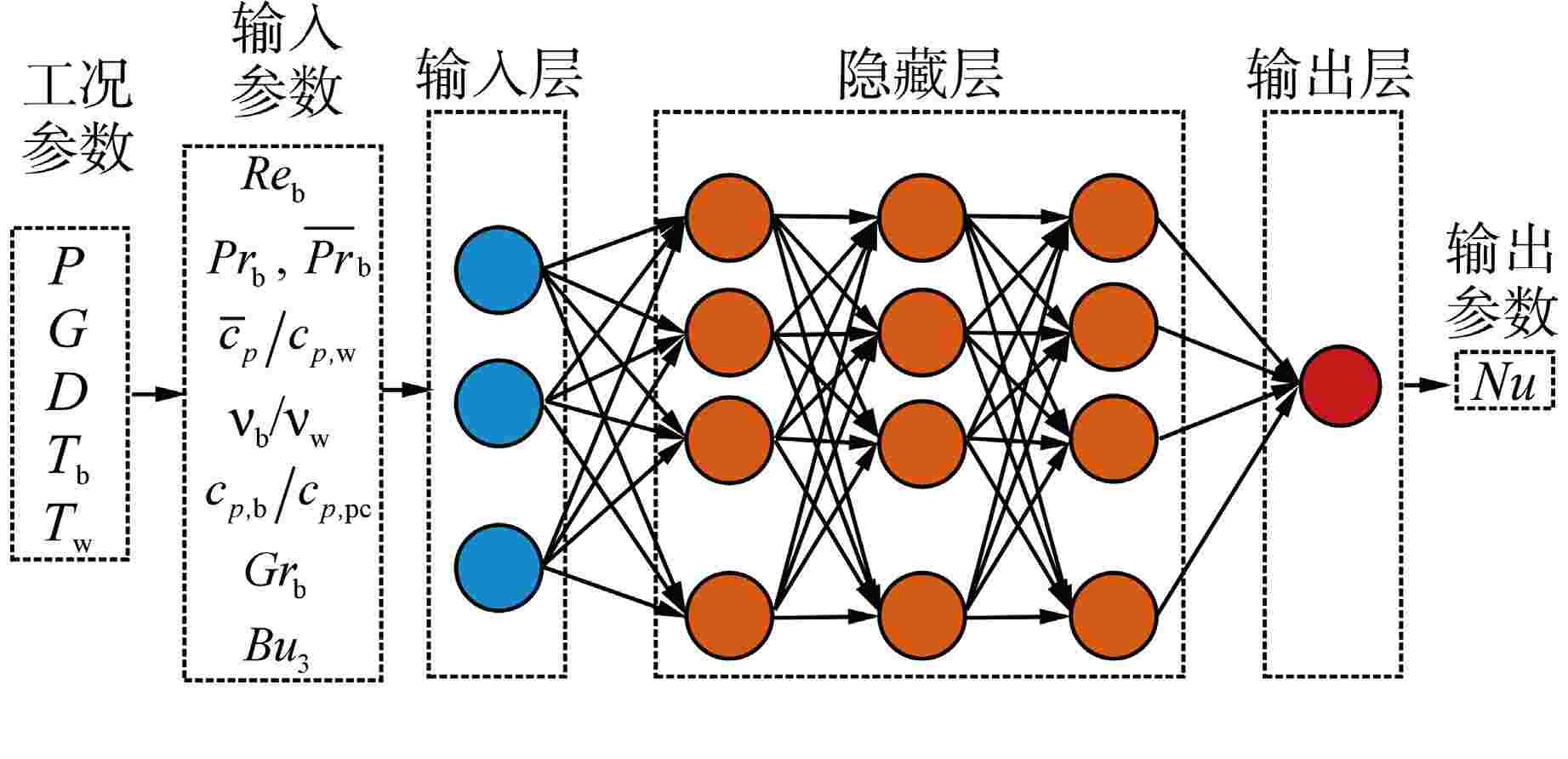
序号 无量纲数 序号 无量纲数 1 $R{e_{\text{b}}}$ 12 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{w}}}}}}$ 2 $P{r_{\text{b}}}$ 13 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{b}}}}}}$ 3 $R{e_{\text{w}}}$ 14 $\dfrac{{{{\bar c}_p}}}{{{c_{p,{\text{w}}}}}}$ 4 $R{e_{\text{f}}}$ 15 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{{\text{pc}}}}}}$ 5 $P{r_{\text{w}}}$ 16 $\dfrac{{{k_{\text{b}}}}}{{{k_{{\text{pc}}}}}}$ 6 ${\overline {Pr} _{\text{b}}}$ 17 $\dfrac{{{c_{p,{\text{b}}}}}}{{{c_{p,{\text{pc}}}}}}$ 7 ${\overline {Pr} _{\text{w}}}$ 18 $ Gr_{\text{b}}=\dfrac{\left(\rho_{\text{b}}-\rho_{\text{w}}\right)gd^3}{\rho_{\text{b}}\mathit{\upsilon}_{\text{b}}^2} $ 8 $\dfrac{{{\mu _{\text{b}}}}}{{{\mu _{\text{w}}}}}$ 19 $B{u_1} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^2}}$ 9 $\dfrac{{{k_{\text{b}}}}}{{{k_{\text{w}}}}}$ 20 $B{u_2} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.7}}}$ 10 $\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}$ 21 $B{u_3} = \dfrac{{G{r_{\text{b}}}}}{{Re_{\text{b}}^{2.625}Pr_{\text{w}}^{{\text{0}}{\text{.4}}}}}{\left( {\dfrac{{{\rho _{\text{b}}}}}{{{\rho _{\text{w}}}}}} \right)^{0.5}}\left( {\dfrac{{{\mu _{\text{w}}}}}{{{\mu _{\text{b}}}}}} \right)$ 11 $\dfrac{{{\nu _{\text{b}}}}}{{{\nu _{\text{w}}}}}$ 表 2 超参数搜索空间及搜索结果
Table 2. Hyper Parameters Search Space and Results
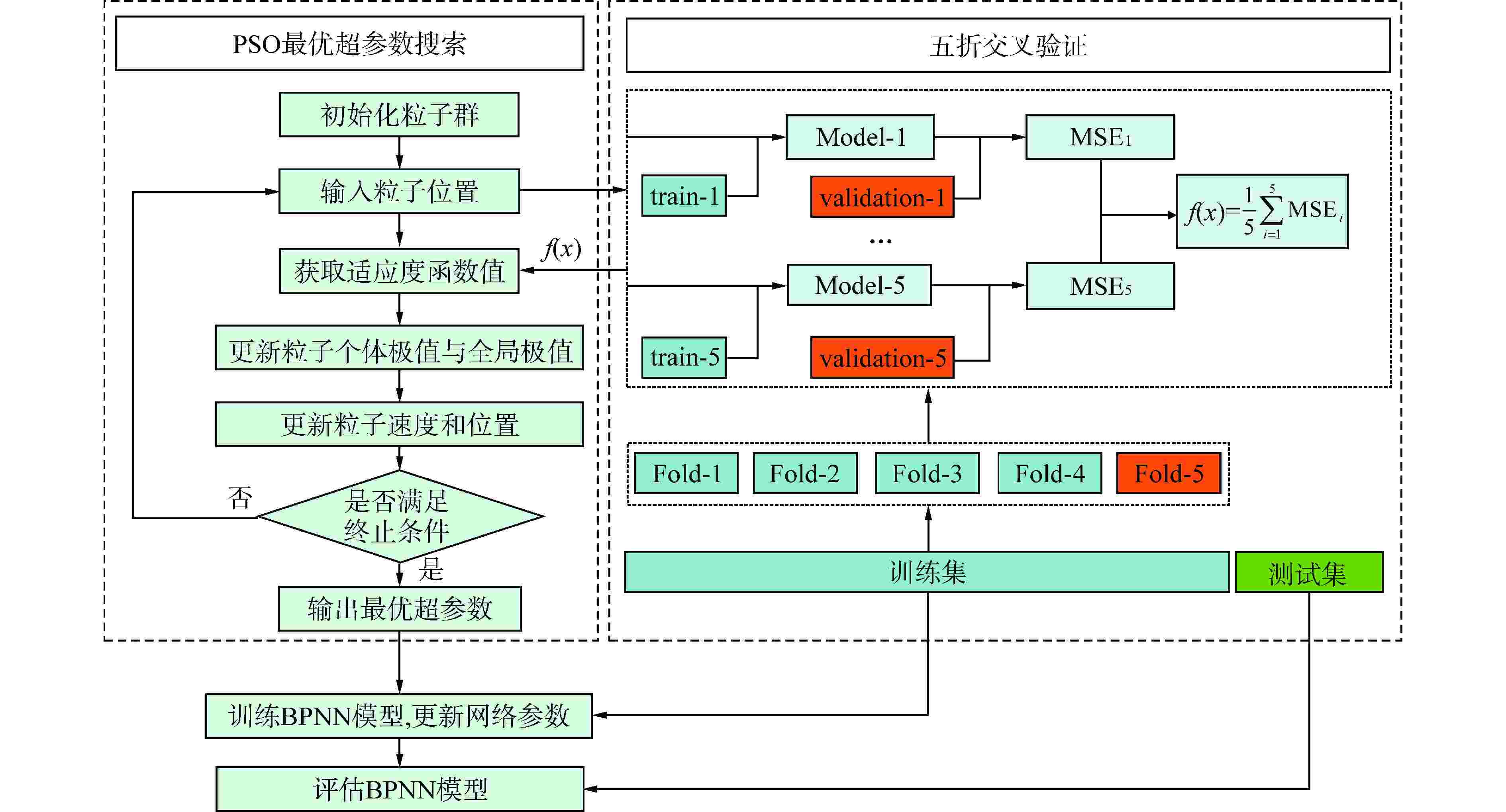
超参数名称 搜索范围 搜索结果 隐藏层数 1~4 2 隐藏层节点数 1~300 119、196 初始学习率 0.00009~0.009 3.0521×10−3 批数量 2~128 115 迭代次数 500~3000 2352 表 3 5%和10%预测误差对应数据占比
Table 3. Proportion of Data Corresponding to the 5% and 10% Prediction Errors
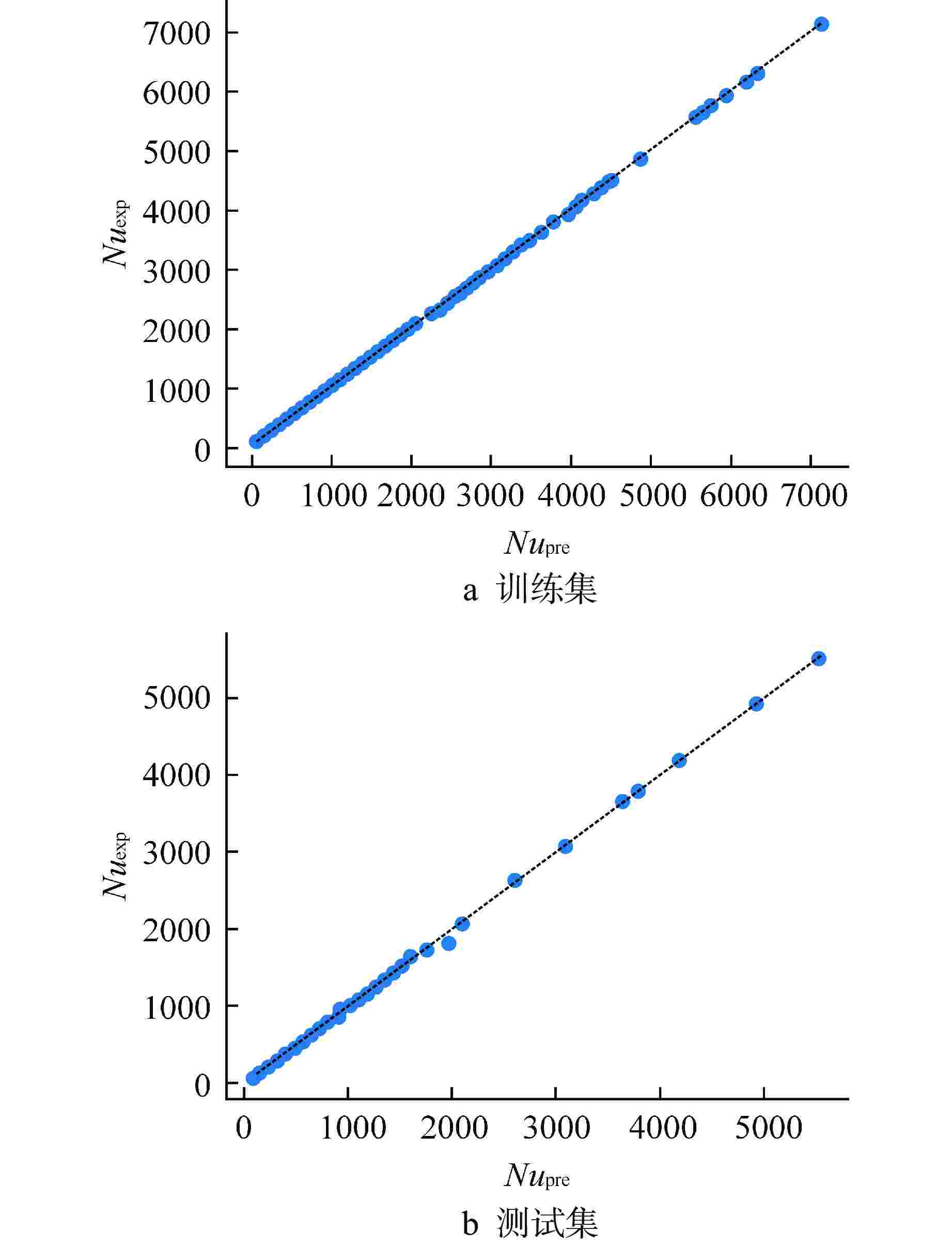
数据集 ${\eta _{5\text{%} }}$ ${\eta _{10\text{%} }}$ 训练集 98.74% 99.76% 测试集 95.31% 98.12% ${\eta _{5\text{%} }}$—预测误差小于5%的数据比例;${\eta _{10\text{%} }}$—预测误差小于5%的数据比例 表 4 数据集误差
Table 4. Dataset Error
数据集 MAPE/% RMSE R2 训练集 0.8 7.0 0.99991 测试集 1.4 18.8 0.99921 表 5 BPNN与现有关联式比对结果
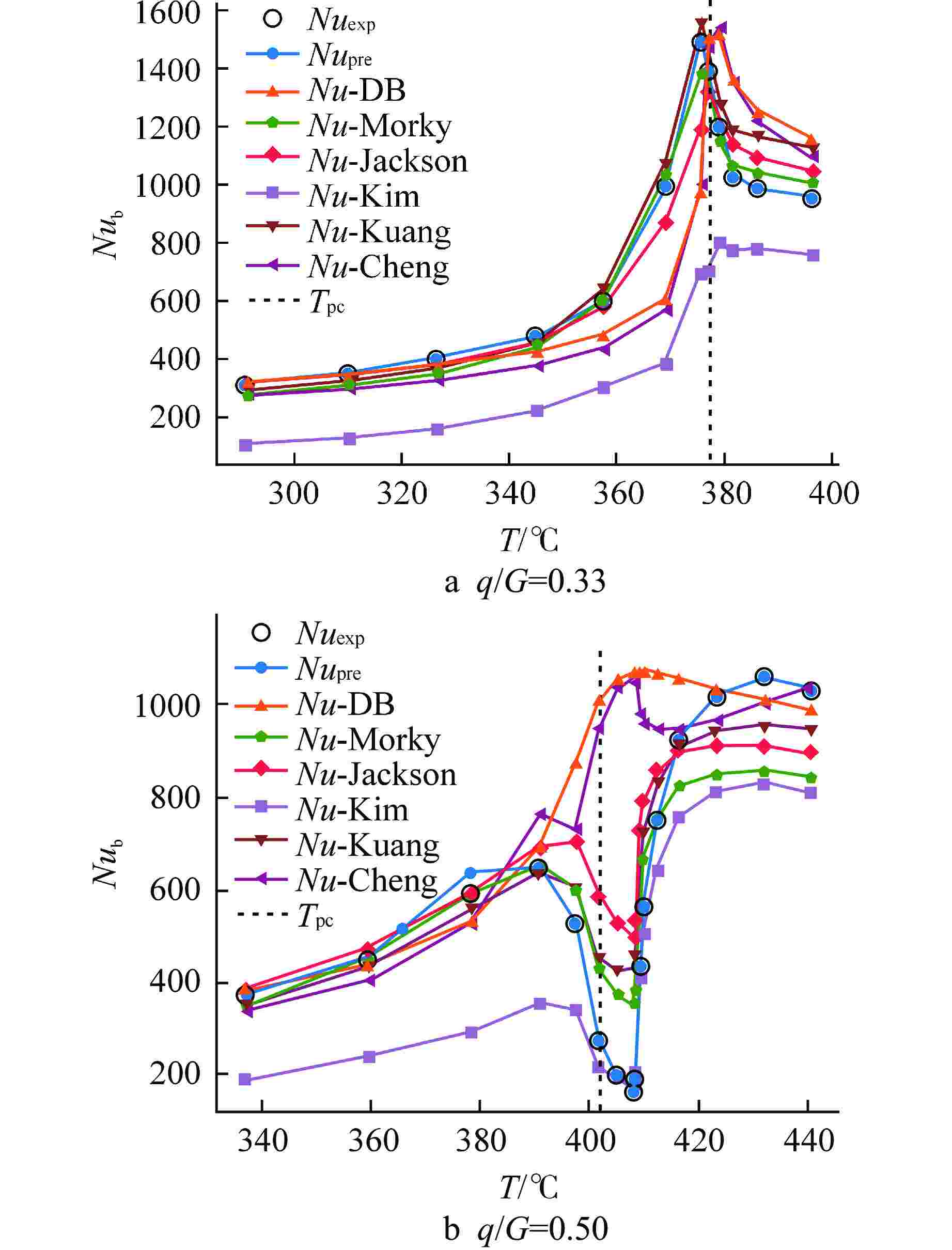
Table 5. Comparison Results between BPNN and Existing Correlations
表 6 不同模型的对比结果
Table 6. Comparison of Different Models
模型 训练时间/s MAPE/% RMSE R2 SVR 13.46 3.9 50.9 0.994 RFR 24.63 3.5 82.3 0.984 BPNN 129.01 1.4 18.8 0.999 -
[1] XIE G N, XU X X, LEI X L, et al. Heat transfer behaviors of some supercritical fluids: a review[J]. Chinese Journal of Aeronautics, 2022, 35(1): 290-306. doi: 10.1016/j.cja.2020.12.022 [2] SWENSON H S, CARVER J R, KAKARALA C R. Heat transfer to supercritical water in smooth-bore tubes[J]. Journal of Heat Transfer, 1965, 87(4): 477-483. doi: 10.1115/1.3689139 [3] PETUKHOV B S. Heat transfer and friction in turbulent pipe flow with variable physical properties[J]. Advances in Heat Transfer, 1970, 6: 503-564. [4] KIM J K, JEON H K, LEE J S. Wall temperature measurement and heat transfer correlation of turbulent supercritical carbon dioxide flow in vertical circular/non-circular tubes[J]. Nuclear Engineering and Design, 2007, 237(15-17): 1795-1802. doi: 10.1016/j.nucengdes.2007.02.017 [5] JACKSON J D. An semi-empirical model of turbulent convective heat transfer to fluids at supercritical pressure[C]//Proceedings of the 16th International Conference on Nuclear Engineering. Orlando: ASME, 2008: 911-921. [6] FANG X D, XU Y. Modified heat transfer equation for in-tube supercritical CO2 cooling[J]. Applied Thermal Engineering, 2011, 31(14-15): 3036-3042. doi: 10.1016/j.applthermaleng.2011.05.037 [7] CHENG X, ZHAO M, FEUERSTEIN F, et al. Prediction of heat transfer to supercritical water at different boundary conditions[J]. International Journal of Heat and Mass Transfer, 2019, 131: 527-536. doi: 10.1016/j.ijheatmasstransfer.2018.11.028 [8] LI Y, CHEN Y Q, ZHANG Y C, et al. An improved heat transfer correlation for supercritical aviation kerosene flowing upward and downward in vertical tubes[J]. Journal of Thermal Science, 2020, 29(1): 131-143. doi: 10.1007/s11630-019-1197-2 [9] CHENG X, KUANG B, YANG Y H. Numerical analysis of heat transfer in supercritical water cooled flow channels[J]. Nuclear Engineering and Design, 2007, 237(3): 240-252. doi: 10.1016/j.nucengdes.2006.06.011 [10] ZHANG B, SHAN J Q, JIANG J. Numerical analysis of supercritical water heat transfer in horizontal circular tube[C]//Proceedings of the 17th International Conference on Nuclear Engineering. Brussels: ICONE, 2009: 471-479. [11] PANDEY S, LAURIEN E, CHU X. A modified convective heat transfer model for heated pipe flow of supercritical carbon dioxide[J]. International Journal of Thermal Sciences, 2017, 117: 227-238. doi: 10.1016/j.ijthermalsci.2017.03.021 [12] ZVORYKIN A, FIALKO N, JULII S, et al. CFD study on specifics of flow and heat transfer in vertical bare tubes cooled with water at supercritical pressures[C]//Proceedings of the 25th International Conference on Nuclear Engineering, Shanghai: AS ME, 2017: V009T15A013. [13] XU K K, RUAN B, MENG H. Validation and analyses of RANS CFD models for turbulent heat transfer of hydrocarbon fuels at supercritical pressures[J]. International Journal of Thermal Sciences, 2018, 124: 212-226. doi: 10.1016/j.ijthermalsci.2017.10.019 [14] YANG Z, CHENG X, ZHENG X H, et al. Reynolds-averaged Navier-Stokes equations describing turbulent flow and heat transfer behavior for supercritical fluid[J]. Journal of Thermal Science, 2021, 30(1): 191-200. doi: 10.1007/s11630-020-1339-6 [15] LIU X J, SONG M Q, CHENG X. Current status and challenges of supercritical fluid thermal hydraulics[J]. Nuclear Engineering and Design, 2019, 354: 110176. doi: 10.1016/j.nucengdes.2019.110176 [16] ZHANG R Z, TONG W T, XU S Y, et al. ANN model with feature selection to predict turbulent heat transfer characteristics of supercritical fluids: take CO2 and H2O as examples[J]. International Journal of Thermal Sciences, 2023, 188: 108247. doi: 10.1016/j.ijthermalsci.2023.108247 [17] AMARDEEP S, SALIGRAM A K, KASHYAP S R, et al. Heat transfer characteristics for upward flow of supercritical water in a vertical pipe–computational fluid dynamics analysis and artificial neural network prediction[J]. International Journal of Thermal Sciences, 2023, 184: 107990. doi: 10.1016/j.ijthermalsci.2022.107990 [18] MA D L, ZHOU T, CHEN J, et al. Supercritical water heat transfer coefficient prediction analysis based on BP neural network[J]. Nuclear Engineering and Design, 2017, 320: 400-408. doi: 10.1016/j.nucengdes.2017.06.013 [19] SUN F, XIE G N, LI S L. An artificial-neural-network based prediction of heat transfer behaviors for in-tube supercritical CO2 flow[J]. Applied Soft Computing, 2021, 102: 107110. doi: 10.1016/j.asoc.2021.107110 [20] PESTEEI S M, MEHRABI M. Modeling of convection heat transfer of supercritical carbon dioxide in a vertical tube at low Reynolds numbers using artificial neural network[J]. International Communications in Heat and Mass Transfer, 2010, 37(7): 901-906. doi: 10.1016/j.icheatmasstransfer.2010.05.018 [21] GUIDOTTI R, MONREALE A, RUGGIERI S, et al. A survey of methods for explaining black box models[J]. ACM Computing Surveys (CSUR), 2018, 51(5): 93. [22] Hall W B, Jackson J D, Watson A. Paper 3: A review of forced convection heat transfer to fluids at supercritical pressures[C]//Proceedings of the institution of mechanical engineers, conference proceedings. Sage UK: London, England: SAGE Publications, 1967, 182(9): 10-22. [23] JIANG P X, ZHANG Y, ZHAO C R, et al. Convection heat transfer of CO2 at supercritical pressures in a vertical mini tube at relatively low Reynolds numbers[J]. Experimental Thermal and Fluid Science, 2008, 32(8): 1628-1637. doi: 10.1016/j.expthermflusci.2008.05.006 [24] LIU S H, HUANG Y P, LIU G X, et al. Improvement of buoyancy and acceleration parameters for forced and mixed convective heat transfer to supercritical fluids flowing in vertical tubes[J]. International Journal of Heat and Mass Transfer, 2017, 106: 1144-1156. doi: 10.1016/j.ijheatmasstransfer.2016.10.093 [25] HE K M, ZHANG X Y, REN S Q, et al. Delving deep into rectifiers: surpassing human-level performance on imagenet classification[C]//Proceedings of 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015: 1026-1034. [26] CARVALHO D V, PEREIRA E M, CARDOSO J S. Machine learning interpretability: A survey on methods and metrics[J]. Electronics, 2019, 8(8): 832. doi: 10.3390/electronics8080832 [27] SUDJIANTO A, ZHANG A. Designing inherently interpretable machine learning models[J]. 2021. DOI: 10.48550/arXiv.2111.01743. [28] DITTUS F W, BOELTER L M K. Heat transfer in automobile radiators of the tubular type[J]. International Communications in Heat and Mass Transfer, 1985, 12(1): 3-22. doi: 10.1016/0735-1933(85)90003-X [29] MOKRY S, PIORO I, FARAH A, et al. Development of supercritical water heat-transfer correlation for vertical bare tubes[J]. Nuclear Engineering and Design, 2011, 241(4): 1126-1136. doi: 10.1016/j.nucengdes.2010.06.012 [30] JACKSON J D. Fluid flow and convective heat transfer to fluids at supercritical pressure[J]. Nuclear Engineering and Design, 2013, 264: 24-40. doi: 10.1016/j.nucengdes.2012.09.040 [31] CHENG X, YANG Y H, HUANG S F. A simplified method for heat transfer prediction of supercritical fluids in circular tubes[J]. Annals of Nuclear Energy, 2009, 36(8): 1120-1128. doi: 10.1016/j.anucene.2009.04.016 [32] XIN L, BO K. Wide-ranged heat transfer correlations of supercritical water in vertical upward channels[J]. Nuclear Science & Engineering, 2012, 32(4): 344-353. [33] KIM D E, KIM M H. Experimental investigation of heat transfer in vertical upward and downward supercritical CO2 flow in a circular tube[J]. International Journal of Heat and Fluid Flow, 2011, 32(1): 176-191. doi: 10.1016/j.ijheatfluidflow.2010.09.001 -





 下载:
下载: