Application of Artificial Intelligence Algorithms in Thermal-Hydraulic Analysis of Nuclear Reactors
-
摘要: 人工智能算法快速预测、自学习与强泛用性的优势已应用于解决核反应堆热工水力现象和机理复杂的问题,包括热工水力参数预测、热工安全分析程序优化与计算流体动力学(CFD)效率提升等。本文回顾了人工智能算法在流型、沸腾换热及临界流等热工水力参数预测研究现状,针对严苛运行条件下机理不明、预测范围局限性问题,基于人工智能非线性快速预测优势扩展分析范围与精度;针对热工分析程序受限于参数模型的问题,利用人工智能自学习、自适应与极强泛用性优势,通过模型校准及数据同化技术提升复杂现象参数识别能力与预测性能;基于模型降阶与快速预测,提高热工水力物理场复杂现象参数的计算效率和多维复现重构能力。提出人工智能算法在反应堆系统大型关键设备全寿期准确预测、液态金属快堆等新型先进反应堆的加快设计迭代、跨尺度多物理场复杂交互的加速优化的未来应用前景。
-
关键词:
- 人工智能 /
- 核反应堆热工水力 /
- 计算流体动力学(CFD) /
- 热工水力参数预测 /
- 安全分析程序
Abstract: The advantages of artificial intelligence (AI) algorithms in rapid prediction, self-learning, and strong generalizability have been applied to address the complexities of thermal-hydraulic phenomena and mechanisms in nuclear reactors. These applications include predictions of thermal-hydraulic parameters, optimization of thermal safety analysis codes, and enhancements in computational fluid dynamics (CFD) efficiency. This paper reviews the current state of research on AI algorithms in predicting thermal-hydraulic parameters such as flow regimes, boiling heat transfer, and critical flow. To address challenges such as unknown mechanisms and limited prediction ranges under extreme operating conditions, this study leverages the nonlinear rapid prediction capabilities of AI to expand the scope and accuracy of analyses. For thermal analysis codes constrained by parameter models, the self-learning, adaptive, and highly generalizable features of AI are utilized to improve the identification and prediction of complex phenomenon parameters through model calibration and data assimilation techniques. By employing model reduction and fast prediction methods, AI enhances the computational efficiency and the multidimensional reconstruction of complex thermal-hydraulic physical fields. Furthermore, the study highlights the future prospects of AI algorithms in accurately predicting the full lifecycle performance of key components in large-scale reactor systems, accelerating design iterations for advanced reactors such as liquid-metal fast reactors, and optimizing cross-scale, multiphysics interactions in a more efficient manner. -
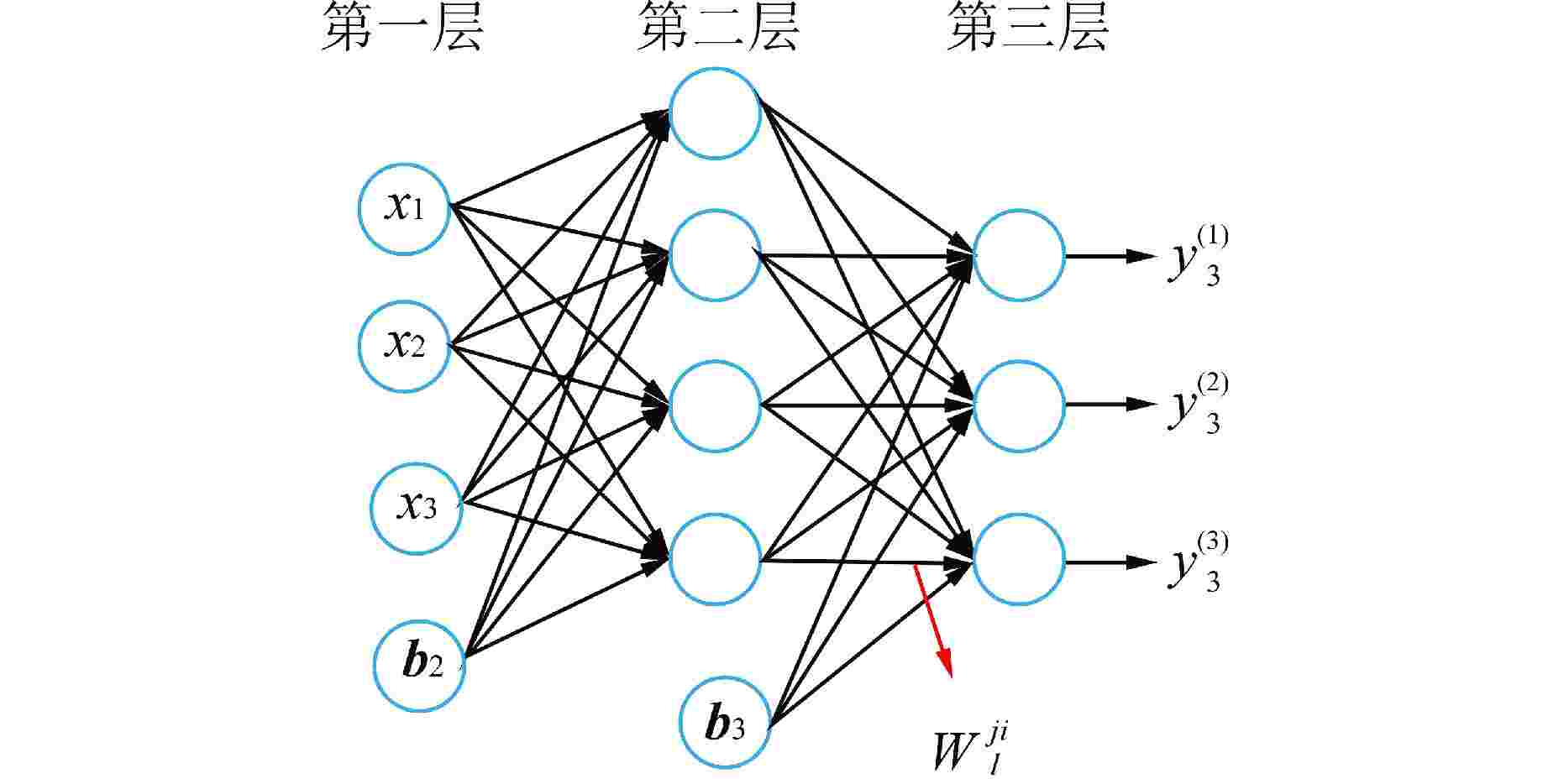
图 2 神经网络基本结构[3]
x—输入参数;y—输出参数;b—矢量,不同节点偏置量可能不一样;W—权重;l—第l层;j—第l层的j节点连接;i—第(l−1)层的i节点
Figure 2. Basic Structure of Neural Networks
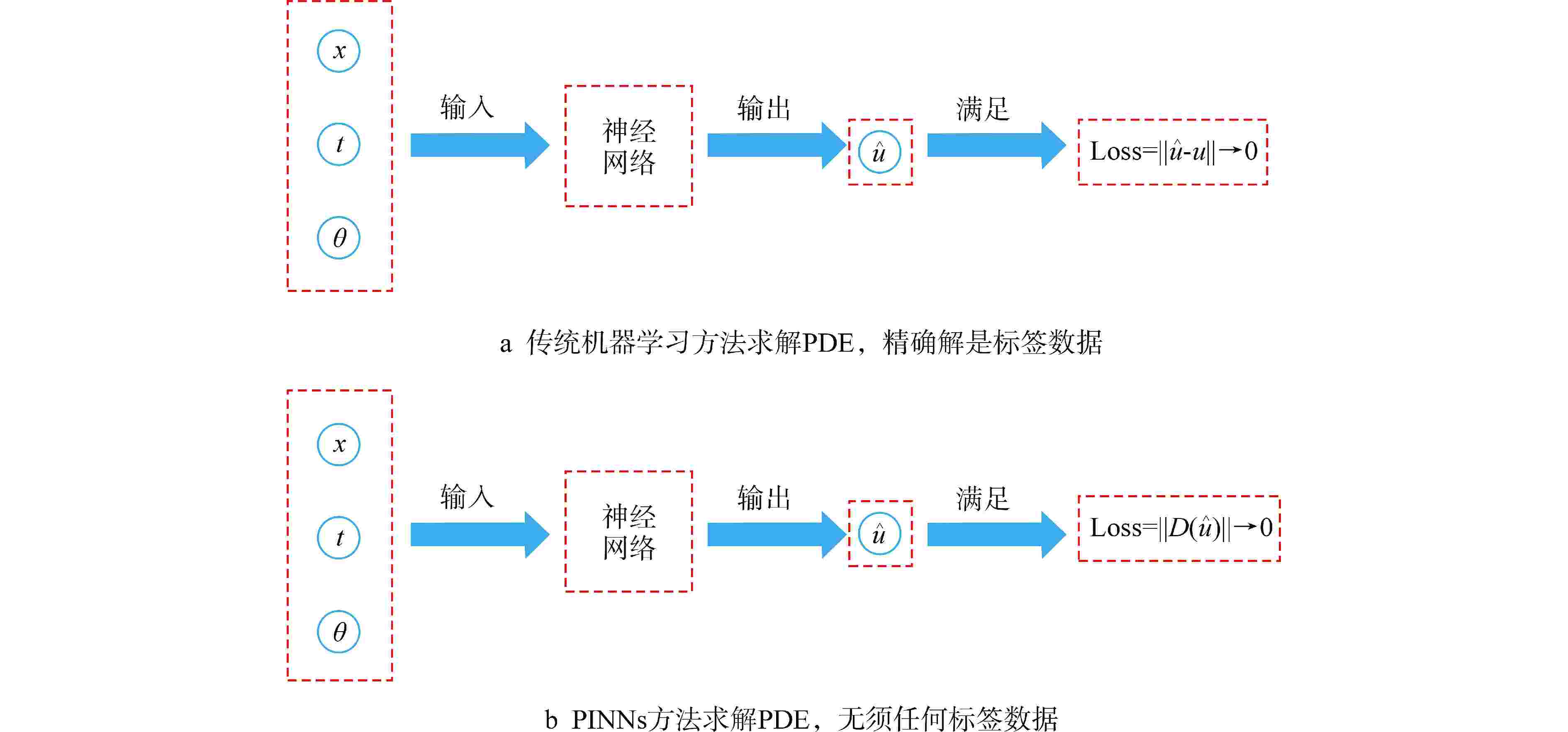
图 3 基于PDE智能求解方法的两种技术路线[9]
t—时间;θ—与空间相关的参数;$ \hat u $—模型计算的数值解;u—微分方程的解析解;Loss—模型计算结果与目标结果之间的差值;D($ \hat u $)—目标函数$ \hat u $的梯度;PDE—偏微分方程
Figure 3. Two Technological Approaches for Intelligent Solving Methods Based on PDEs
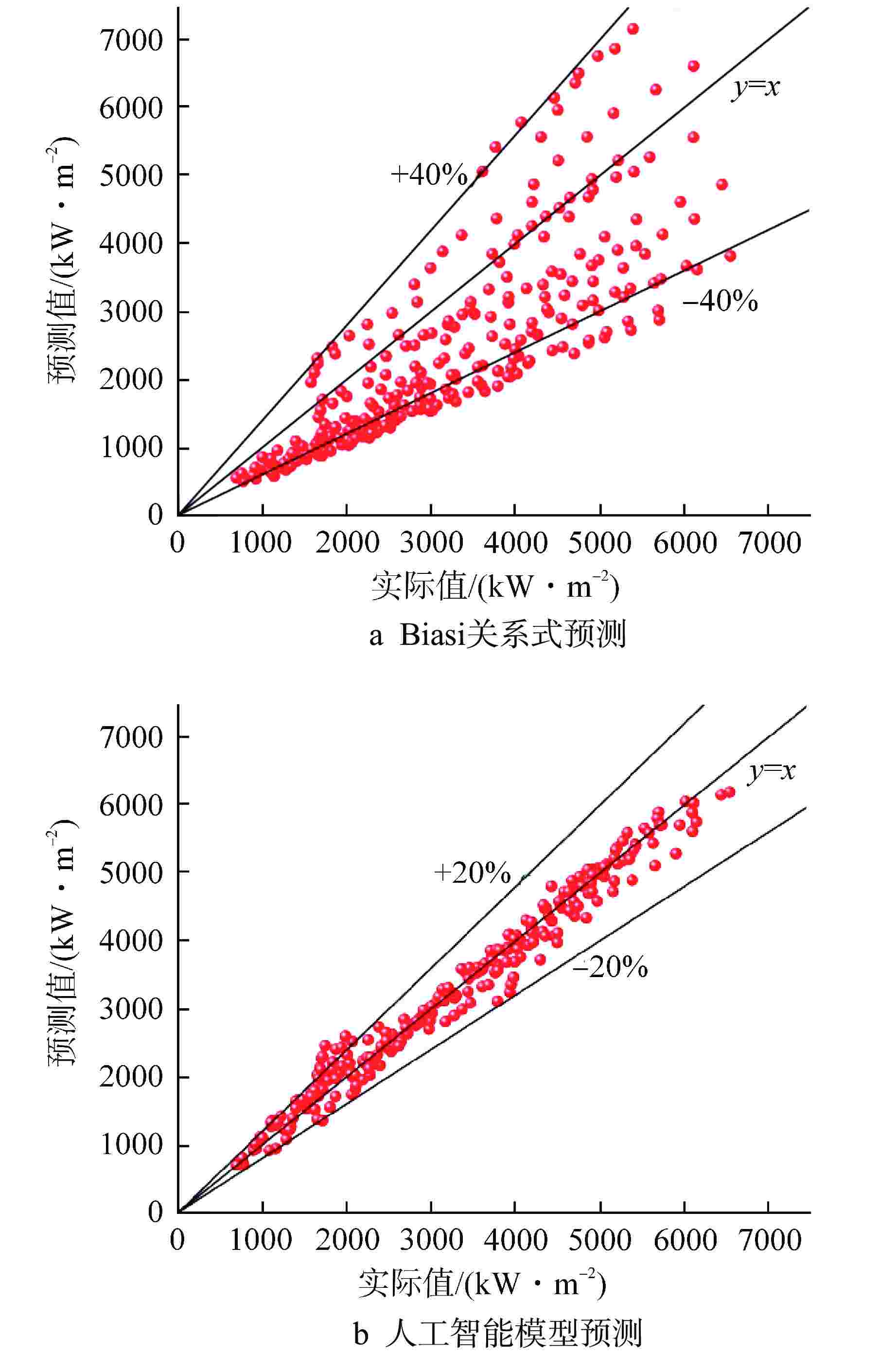
图 6 基于人工智能算法和传统经验关系式的CHF预测[39]
Figure 6. Prediction of CHF Based on AI Algorithms and Traditional Empirical Correlations
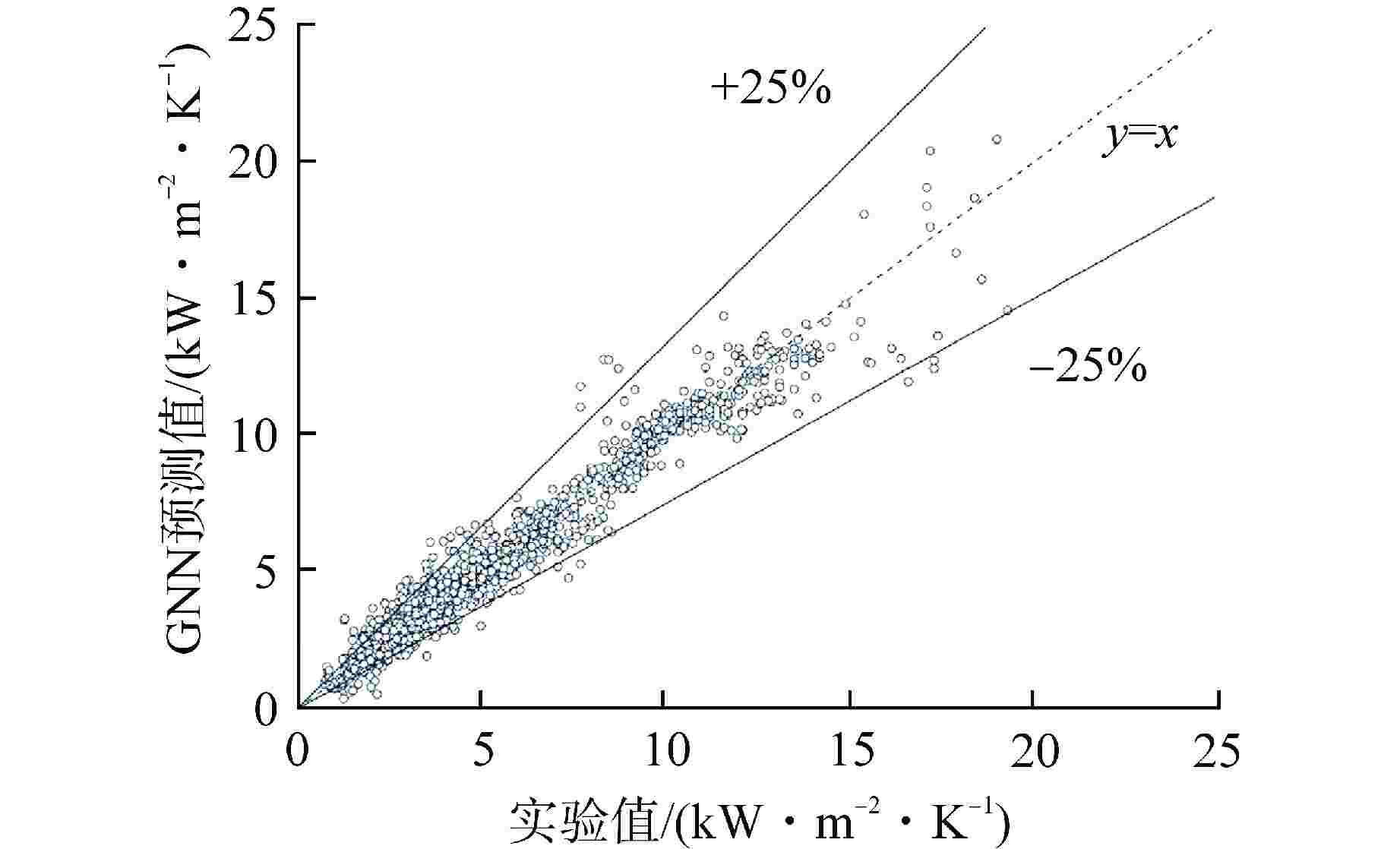
图 7 基于人工智能算法的沸腾换热系数预测[44]
Figure 7. Prediction of Boiling Heat Transfer Coefficient Based on AI Algorithms
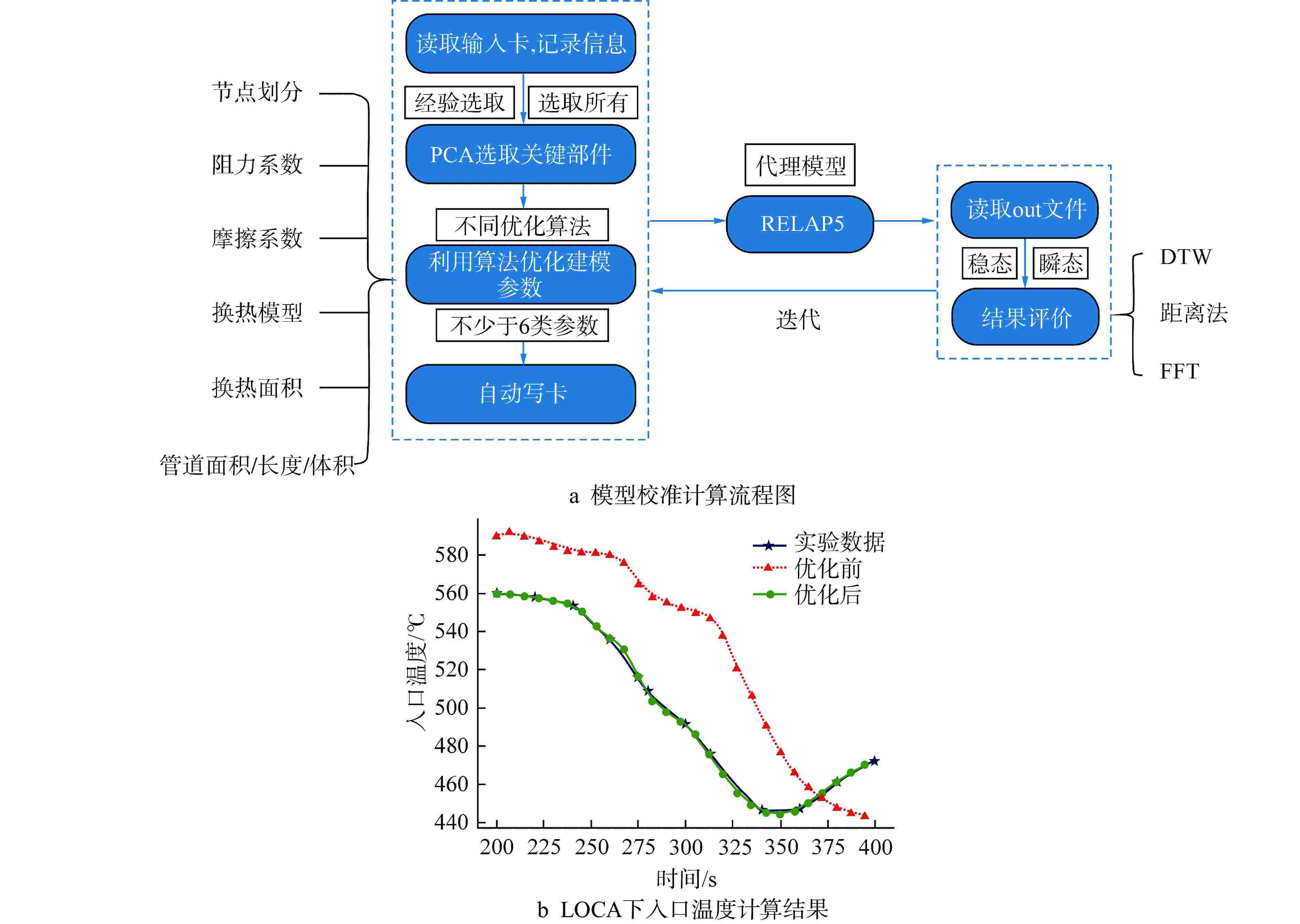
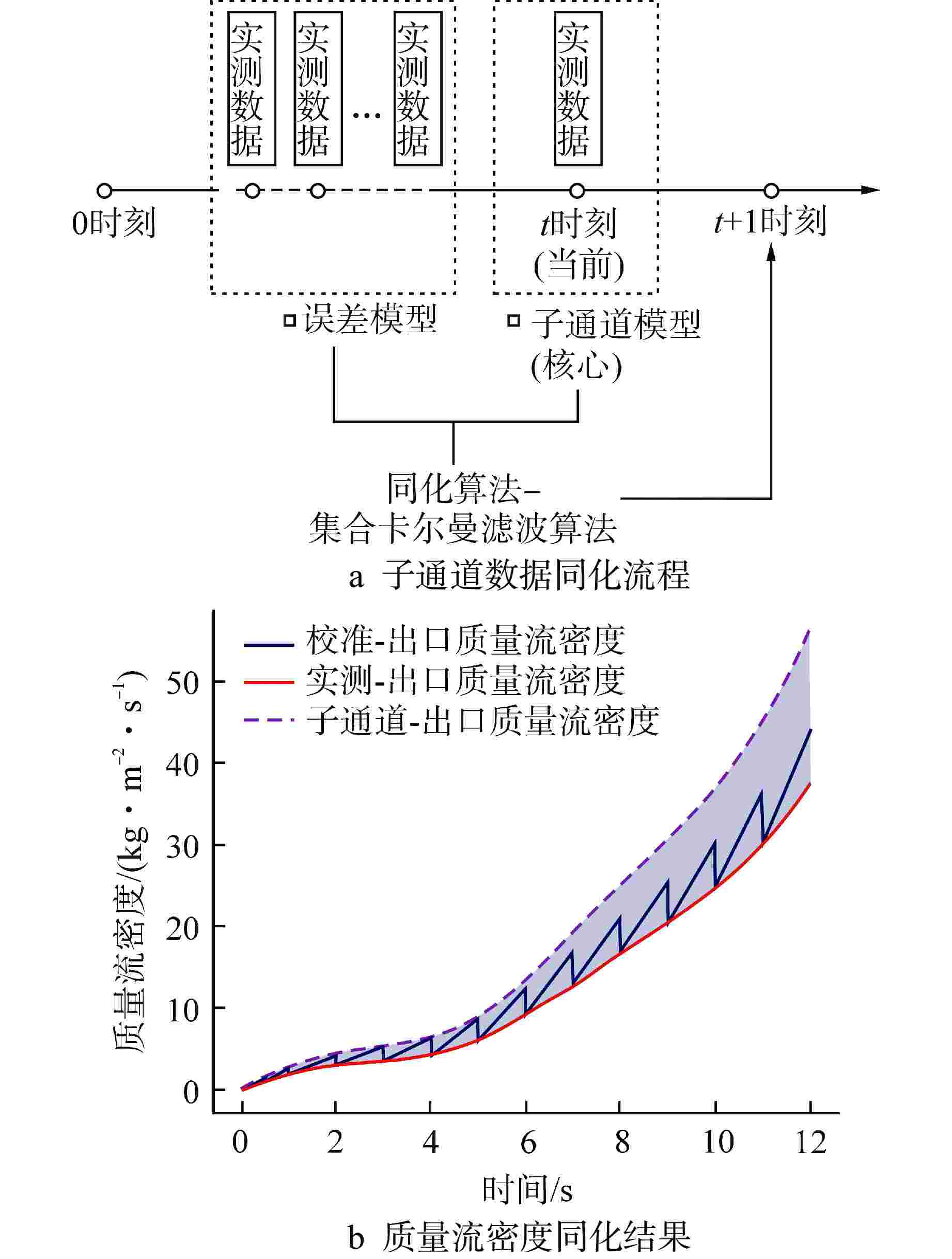
图 9 基于人工智能模型的系统分析程序优化[39]
HTC—换热系数
Figure 9. Optimization of System Analysis Codes Based on AI Models
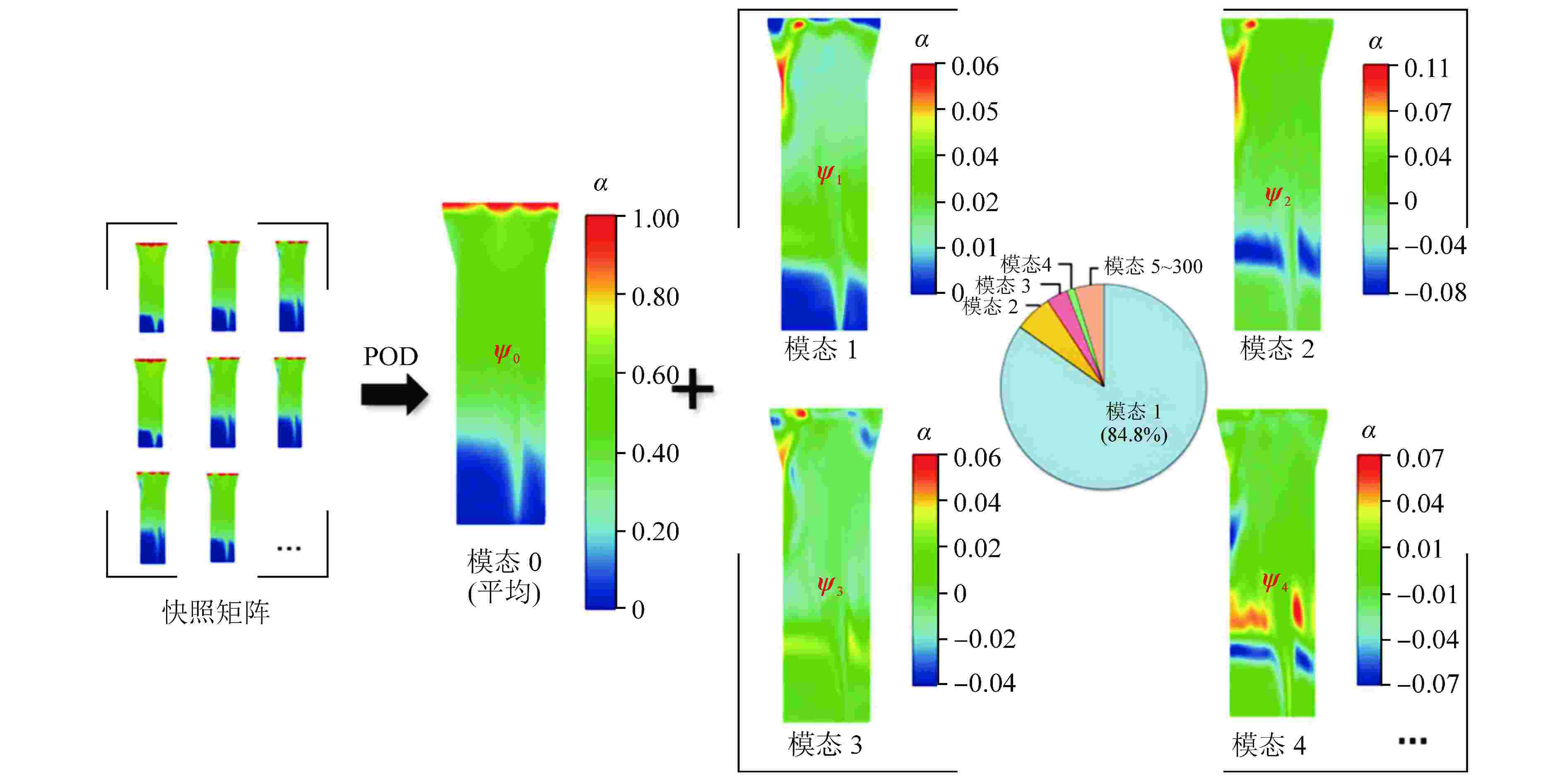
图 12 基于模型降阶的蒸汽发生器三维热工水力参数预测[84]
α—空泡份额;模态0~4—POD分析中提取的主要特征向量;ψ1~4—第1~4阶正交基向量
Figure 12. Prediction of Three-dimensional Thermal-hydraulic Parameters of a Steam Generator Based on Model Order Reduction
-
[1] FAROUGHI S A, PAWAR N M, FERNANDES C, et al. Physics-guided, physics-informed, and physics-encoded neural networks and operators in scientific computing: fluid and solid mechanics[J]. Journal of Computing and Information Science in Engineering, 2024, 24(4): 040802. doi: 10.1115/1.4064449 [2] YAO X. A review of evolutionary artificial neural networks[J]. International Journal of Intelligent Systems, 1993, 8(4): 539-567. doi: 10.1002/int.4550080406 [3] 章静,丛腾龙,苏光辉,等. 遗传神经网络对水平通道流动沸腾传热系数的预测[J]. 原子能科学技术,2015, 49(1): 70-76. doi: 10.7538/yzk.2015.49.01.0070 [4] SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural Networks, 2015, 61: 85-117. doi: 10.1016/j.neunet.2014.09.003 [5] BALCILAR M, DALKILIC A S, WONGWISES S. Artificial neural network techniques for the determination of condensation heat transfer characteristics during downward annular flow of R134a inside a vertical smooth tube[J]. International Communications in Heat and Mass Transfer, 2011, 38(1): 75-84. doi: 10.1016/j.icheatmasstransfer.2010.10.009 [6] ABDI H, VALENTIN D, EDELMAN B. Neural networks[M]. Thousand Oaks: Sage Publications, 1999: 1-96. [7] GOLDBERG D E, DEB K. A comparative analysis of selection schemes used in genetic algorithms[J]. Foundations of Genetic Algorithms, 1991, 1: 69-93. [8] CUOMO S, DI COLA V S, GIAMPAOLO F, et al. Scientific machine learning through physics–informed neural networks: where we are and what's next[J]. Journal of Scientific Computing, 2022, 92(3): 88. doi: 10.1007/s10915-022-01939-z [9] 查文舒,李道伦,沈路航,等. 基于神经网络的偏微分方程求解方法研究综述[J]. 力学学报,2022, 54(3): 543-556. doi: 10.6052/0459-1879-21-617 [10] LIN P Y, HANRATTY T J. Effect of pipe diameter on flow patterns for air-water flow in horizontal pipes[J]. International Journal of Multiphase Flow, 1987, 13(4): 549-563. doi: 10.1016/0301-9322(87)90021-8 [11] MANDHANE J M, GREGORY G A, AZIZ K. A flow pattern map for gas-liquid flow in horizontal pipes[J]. International Journal of Multiphase Flow, 1974, 1(4): 537-553. doi: 10.1016/0301-9322(74)90006-8 [12] BARNEA D, LUNINSKI Y, TAITEL Y. Flow pattern in horizontal and vertical two phase flow in small diameter pipes[J]. The Canadian Journal of Chemical Engineering, 1983, 61(5): 617-620. doi: 10.1002/cjce.5450610501 [13] YANG Z J, DANG Z R, YANG X H, et al. Downward two phase flow experiment and general flow regime transition criteria for various pipe sizes[J]. International Journal of Heat and Mass Transfer, 2018, 125: 179-189. doi: 10.1016/j.ijheatmasstransfer.2018.03.072 [14] LEE J Y, ISHII M, KIM N S. Instantaneous and objective flow regime identification method for the vertical upward and downward co-current two-phase flow[J]. International Journal of Heat and Mass Transfer, 2008, 51(13-14): 3442-3459. doi: 10.1016/j.ijheatmasstransfer.2007.10.037 [15] PARANJAPE S, CHEN S W, HIBIKI T, et al. Flow regime identification under adiabatic upward two-phase flow in a vertical rod bundle geometry[J]. Journal of Fluids Engineering, 2011, 133(9): 091302. doi: 10.1115/1.4004836 [16] PAN L M, ZHANG M H, JU P, et al. Vertical co-current two-phase flow regime identification using fuzzy C-means clustering algorithm and ReliefF attribute weighting technique[J]. International Journal of Heat and Mass Transfer, 2016, 95: 393-404. doi: 10.1016/j.ijheatmasstransfer.2015.11.081 [17] TAMBOURATZIS T, PÀZSIT I. A general regression artificial neural network for two-phase flow regime identification[J]. Annals of Nuclear Energy, 2010, 37(5): 672-680. doi: 10.1016/j.anucene.2010.02.004 [18] OUYANG L, JIN N D, REN W K. A new deep neural network framework with multivariate time series for two-phase flow pattern identification[J]. Expert Systems with Applications, 2022, 205: 117704. doi: 10.1016/j.eswa.2022.117704 [19] MA Y C, KONG D X, ZHANG J, et al. Study on flow regime prediction model for water-cooled reactor core based on machine learning algorithms[J]. Annals of Nuclear Energy, 2024, 201: 110428. doi: 10.1016/j.anucene.2024.110428 [20] LIU W, NARIAI H. Ultrahigh CHF prediction for subcooled flow boiling based on homogenous nucleation mechanism[J]. Journal of Heat Transfer, 2005, 127(2): 149-158. doi: 10.1115/1.1844536 [21] WEISMAN J, ILESLAMLOU S. A phenomenological model for prediction of critical heat flux under highly subcooled conditions[J]. Fusion Technology, 1988, 13(4): 654-659. doi: 10.13182/FST88-A25140 [22] KWON Y M, CHANG S H. A mechanistic critical heat flux model for wide range of subcooled and low quality flow boiling[J]. Nuclear Engineering and Design, 1999, 188(1): 27-47. doi: 10.1016/S0029-5493(99)00025-4 [23] KATTO Y. A prediction model of subcooled water flow boiling CHF for pressure in the range 0.1-20 MPa[J]. International Journal of Heat and Mass Transfer, 1992, 35(5): 1115-1123. doi: 10.1016/0017-9310(92)90172-O [24] LEE C H, MUDAWWAR I. A mechanistic critical heat flux model for subcooled flow boiling based on local bulk flow conditions[J]. International Journal of Multiphase Flow, 1988, 14(6): 711-728. doi: 10.1016/0301-9322(88)90070-5 [25] CELATA G P, CUMO M, MARIANI A, et al. Rationalization of existing mechanistic models for the prediction of water subcooled flow boiling critical heat flux[J]. International Journal of Heat and Mass Transfer, 1994, 37(S1): 347-360. [26] LIU W, NARIAI H, INASAKA F. Prediction of critical heat flux for subcooled flow boiling[J]. International Journal of Heat and Mass Transfer, 2000, 43(18): 3371-3390. doi: 10.1016/S0017-9310(99)00373-7 [27] PAYAN-RODRIGUEZ L A, GALLEGOS-MUÑOZ A, PORRAS-LOAIZA G L, et al. Critical heat flux prediction for water boiling in vertical tubes of a steam generator[J]. International Journal of Thermal Sciences, 2005, 44(2): 179-188. doi: 10.1016/j.ijthermalsci.2004.05.003 [28] 周磊,闫晓,黄善仿,等. 基于矩形窄缝通道实验数据的DNB机理模型评价[J]. 原子能科学技术,2011, 45(11): 1317-1323. doi: 10.7538/yzk.2011.45.11.1317 [29] VAN DER MOLEN S B, GALJEE F W B M. The boiling mechanism during burnout phenomena in subcooled two-phase water flows[J]. Flow Boiling and Two-Phase, 1978, 1: 381-385. [30] MOON S K, CHANG S H. Classification and prediction of the critical heat flux using fuzzy theory and artificial neural networks[J]. Nuclear Engineering and Design, 1994, 150(1): 151-161. doi: 10.1016/0029-5493(94)90059-0 [31] MAZZOLA A. Integrating artificial neural networks and empirical correlations for the prediction of water-subcooled critical heat flux[J]. Revue Générale de Thermique, 1997, 36(11): 799-806. [32] GUANGHUI S, MORITA K, FUKUDA K, et al. Analysis of the critical heat flux in round vertical tubes under low pressure and flow oscillation conditions. Applications of artificial neural network[J]. Nuclear Engineering and Design, 2003, 220(1): 17-35. doi: 10.1016/S0029-5493(02)00304-7 [33] ZHAO X G, SHIRVAN K, SALKO R K, et al. On the prediction of critical heat flux using a physics-informed machine learning-aided framework[J]. Applied Thermal Engineering, 2020, 164: 114540. doi: 10.1016/j.applthermaleng.2019.114540 [34] CHEN R H, SU G H, QIU S Z, et al. Prediction of CHF in concentric-tube open thermosiphon using artificial neural network and genetic algorithm[J]. Heat and Mass Transfer, 2010, 46(3): 345-353. doi: 10.1007/s00231-010-0575-9 [35] CONG T L, SU G G, QIU S Z, et al. Applications of ANNs in flow and heat transfer problems in nuclear engineering: a review work[J]. Progress in Nuclear Energy, 2013, 62: 54-71. doi: 10.1016/j.pnucene.2012.09.003 [36] WEI H M, SU G H, TIAN W X, et al. Study on dryout point by wavelet and GNN[J]. Applied Thermal Engineering, 2010, 30(6-7): 664-672. doi: 10.1016/j.applthermaleng.2009.11.014 [37] KIM H, MOON J, HONG D J, et al. Prediction of critical heat flux for narrow rectangular channels in a steady state condition using machine learning[J]. Nuclear Engineering and Technology, 2021, 53(6): 1796-1809. doi: 10.1016/j.net.2020.12.007 [38] ZHANG J F, ZHONG D W, SHI H P, et al. Machine learning prediction of critical heat flux on downward facing surfaces[J]. International Journal of Heat and Mass Transfer, 2022, 191: 122857. doi: 10.1016/j.ijheatmasstransfer.2022.122857 [39] QIU Z F, MA Y C, HUANG T, et al. Development and application of data-driven CHF model in system analysis code[J]. Nuclear Engineering and Design, 2024, 428: 113488. doi: 10.1016/j.nucengdes.2024.113488 [40] CHEN J C. Correlation for boiling heat transfer to saturated fluids in convective flow[J]. Industrial & Engineering Chemistry Process Design and Development, 1966, 5(3): 322-329. [41] SHAH M M. Chart correlation for saturated boiling heat transfer: equations and further study[J]. ASHRAE Transactions, 1982, 88: 165-196. [42] KANDLIKAR S G, STEINKE M E. Predicting heat transfer during flow boiling in minichannels and microchannels[J]. ASHRAE Transactions, 2003, 109: 667-676. [43] JAMBUNATHAN K, HARTLE S L, ASHFORTH-FROST S, et al. Evaluating convective heat transfer coefficients using neural networks[J]. International Journal of Heat and Mass Transfer, 1996, 39(11): 2329-2332. doi: 10.1016/0017-9310(95)00332-0 [44] ZHANG J, MA Y C, WANG M J, et al. Prediction of flow boiling heat transfer coefficient in horizontal channels varying from conventional to small-diameter scales by genetic neural network[J]. Nuclear Engineering and Technology, 2019, 51(8): 1897-1904. doi: 10.1016/j.net.2019.06.009 [45] ZHOU L W, GARG D, QIU Y, et al. Machine learning algorithms to predict flow condensation heat transfer coefficient in mini/micro-channel utilizing universal data[J]. International Journal of Heat and Mass Transfer, 2020, 162: 120351. doi: 10.1016/j.ijheatmasstransfer.2020.120351 [46] BARD A, QIU Y, KHARANGATE C R, et al. Consolidated modeling and prediction of heat transfer coefficients for saturated flow boiling in mini/micro-channels using machine learning methods[J]. Applied Thermal Engineering, 2022, 210: 118305. doi: 10.1016/j.applthermaleng.2022.118305 [47] WEI H M, SU G H, TIAN W X, et al. Study on the characteristic points of boiling curve by using wavelet analysis and genetic neural network[J]. Nuclear Engineering and Design, 2009, 239(11): 2317-2325. doi: 10.1016/j.nucengdes.2009.07.016 [48] WEI H M, SU G H, TIAN W X, et al. Study on the onset of nucleate boiling in narrow annular channel by genetic neural network[J]. International Communications in Heat and Mass Transfer, 2010, 37(6): 596-599. doi: 10.1016/j.icheatmasstransfer.2009.11.017 [49] ZHANG J, CHEN R H, WANG M J, et al. Prediction of LBB leakage for various conditions by genetic neural network and genetic algorithms[J]. Nuclear Engineering and Design, 2017, 325: 33-43. doi: 10.1016/j.nucengdes.2017.09.027 [50] MOODY F J. Closure to “discussions of ‘maximum flow rate of a single component, two-phase mixture’” (1965, ASME J. Heat Transfer, 87, pp. 141–142)[J]. Journal of Heat Transfer, 1965, 87(1): 142. doi: 10.1115/1.3689034 [51] WALLIS G B. One-dimensional two-phase flow[M]. Garden City: Dover Publications, 2020: 1-432. [52] FAUSKE H K. Contribution to the theory of two-phase, one-component critical flow[R]. Argonne: Argonne National Laboratory, 1962. [53] HENRY R E, FAUSKE H K, MCCOMAS S T. Two-phase critical flow at low qualities part I: experimental[J]. Nuclear Science and Engineering, 1970, 41(1): 79-91. doi: 10.13182/NSE70-A20366 [54] 龚禾林,洪历展,赵文博,等. 基于“全局-局部”搜索的核反应堆运行孪生反问题求解[J]. 原子能科学技术,2024, 58(7): 1424-1431. [55] 王伟伟. AP1000典型事故工况瞬态热工水力特性研究[D]. 西安: 西安交通大学,2017. [56] KHUWAILEH B A, TURINSKY P J. Surrogate based model calibration for pressurized water reactor physics calculations[J]. Nuclear Engineering and Technology, 2017, 49(6): 1219-1225. doi: 10.1016/j.net.2017.08.007 [57] LANAHAN M L, ABDEL-KHALIK S I, YODA M. Bayesian parameter estimation of the k-ω shear stress transport model for accurate simulations of impinging-jet heat transfer[J]. Fusion Science and Technology, 2023, 79(8): 1071-1081. doi: 10.1080/15361055.2023.2177065 [58] ZAJTSEV P A, PRIJMAK S V, OLEJNIKOV P P, et al. Models of the drift of the calibration curves of thermocouples and resistance thermometers under reactor conditions[J]. Atomic Energy, 2013, 113(3): 219-221. doi: 10.1007/s10512-012-9620-8 [59] KHVOSTOV G. Calibration and validation of thermal fuel behaviour models based on the first case of the first IAEA CRP FUMEX[J]. Journal of Nuclear Materials, 2023, 584: 154588. doi: 10.1016/j.jnucmat.2023.154588 [60] PERRET G, WICAKSONO D, CLIFFORD I D, et al. Global sensitivity analysis and bayesian calibration on a series of reflood experiments with varying boundary conditions[J]. Nuclear Technology, 2022, 208(4): 711-722. doi: 10.1080/00295450.2021.1936879 [61] LEFEBVRE L, SEGOND M, SPAGGIARI R, et al. Improving the predictivity of a steam generator clogging numerical model by global sensitivity analysis and Bayesian calibration techniques[J]. Nuclear Science and Engineering, 2023, 197(8): 2136-2149. doi: 10.1080/00295639.2023.2206769 [62] 丁政韬. 基于实测数据的反应堆热工水力模型校准及同化技术研究[D]. 西安: 西安交通大学,2024. [63] 宫鹏. 遥感科学与技术中的一些前沿问题[J]. 遥感学报,2009, 13(1): 13-23. [64] 马建文,秦思娴. 数据同化算法研究现状综述[J]. 地球科学进展,2012, 27(7): 747-757. [65] DENG Z W, HE C X, WEN X, et al. Recovering turbulent flow field from local quantity measurement: turbulence modeling using ensemble-Kalman-filter-based data assimilation[J]. Journal of Visualization, 2018, 21(6): 1043-1063. doi: 10.1007/s12650-018-0508-0 [66] SUAREZ G, ZHOU B Y, OEZKAYA E, et al. Towards turbulence modeling enhancement via the correction of Boussinesq’s hypothesis - a data-driven approach[C]//AIAA Aviation 2021 Forum. Virtual Event: American Institute of Aeronautics and Astronautics, 2021. [67] CHANDRAMOULI P, MEMIN E, HEITZ D. 4D variational data assimilation with large eddy simulation[C]//AIAA Aviation 2019 Forum. Dallas: American Institute of Aeronautics and Astronautics, 2019. [68] SAKOE H, CHIBA S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1978, 26(1): 43-49. doi: 10.1109/TASSP.1978.1163055 [69] GILLISSEN J J J, BOUFFANAIS R, YUE D K P. Data assimilation method to de-noise and de-filter particle image velocimetry data[J]. Journal of Fluid Mechanics, 2019, 877: 196-213. doi: 10.1017/jfm.2019.602 [70] PAN Z, ZHANG Y, GUSTAVSSON J P R, et al. Unscented Kalman filter (UKF)–based nonlinear parameter estimation for a turbulent boundary layer: a data assimilation framework[J]. Measurement Science and Technology, 2020, 31(9): 094011. doi: 10.1088/1361-6501/ab8904 [71] ZHENG D, LEUNG J, LEE B, et al. Data assimilation in the atmospheric dispersion model for nuclear accident assessments[J]. Atmospheric Environment, 2007, 41(11): 2438-2446. doi: 10.1016/j.atmosenv.2006.05.076 [72] 袁彪,王良瑜,绪梅,等. 数据同化在核事故辐射场评估中的应用研究[J]. 中国安全科学学报,2015, 25(5): 31-36. [73] SUNDAR S, RAJAGOPAL M C, ZHAO H Y, et al. Fouling modeling and prediction approach for heat exchangers using deep learning[J]. International Journal of Heat and Mass Transfer, 2020, 159: 120112. doi: 10.1016/j.ijheatmasstransfer.2020.120112 [74] HOSSEINI S, KHANDAKAR A, CHOWDHURY M E H, et al. Novel and robust machine learning approach for estimating the fouling factor in heat exchangers[J]. Energy Reports, 2022, 8: 8767-8776. doi: 10.1016/j.egyr.2022.06.123 [75] LI Q, ZHAN Q, YU S P, et al. Study on thermal-hydraulic performance of printed circuit heat exchangers with supercritical methane based on machine learning methods[J]. Energy, 2023, 282: 128711. doi: 10.1016/j.energy.2023.128711 [76] LONGO G A, MANCIN S, RIGHETTI G, et al. Machine learning approach for predicting refrigerant two-phase pressure drop inside Brazed Plate Heat Exchangers (BPHE)[J]. International Journal of Heat and Mass Transfer, 2020, 163: 120450. doi: 10.1016/j.ijheatmasstransfer.2020.120450 [77] EL-SAID E M S, ABD ELAZIZ M, ELSHEIKH A H. Machine learning algorithms for improving the prediction of air injection effect on the thermohydraulic performance of shell and tube heat exchanger[J]. Applied Thermal Engineering, 2021, 185: 116471. doi: 10.1016/j.applthermaleng.2020.116471 [78] ZHU G Y, WEN T, ZHANG D L. Machine learning based approach for the prediction of flow boiling/condensation heat transfer performance in mini channels with serrated fins[J]. International Journal of Heat and Mass Transfer, 2021, 166: 120783. doi: 10.1016/j.ijheatmasstransfer.2020.120783 [79] MOHAMMADPOUR J, HUSAIN S, SALEHI F, et al. Machine learning regression-CFD models for the nanofluid heat transfer of a microchannel heat sink with double synthetic jets[J]. International Communications in Heat and Mass Transfer, 2022, 130: 105808. doi: 10.1016/j.icheatmasstransfer.2021.105808 [80] WANG Q, ZHOU W W, YANG L, et al. Comparison between conventional and deep learning-based surrogate models in predicting convective heat transfer performance of U-bend channels[J]. Energy and AI, 2022, 8: 100140. doi: 10.1016/j.egyai.2022.100140 [81] EOM Y H, CHUNG Y, PARK M, et al. Deep learning-based prediction method on performance change of air source heat pump system under frosting conditions[J]. Energy, 2021, 228: 120542. doi: 10.1016/j.energy.2021.120542 [82] 叶伊博. 基于机器学习的蒸汽发生器污垢热阻及三维温度场快速预测研究[D]. 西安: 西安交通大学,2024. [83] GIRFOGLIO M, QUAINI A, ROZZA G. A POD-Galerkin reduced order model for the Navier–Stokes equations in stream function-vorticity formulation[J]. Computers & Fluids, 2022, 244: 105536. [84] HE S P, WANG M J, ZHANG J, et al. A deep-learning reduced-order model for thermal hydraulic characteristics rapid estimation of steam generators[J]. International Journal of Heat and Mass Transfer, 2022, 198: 123424. doi: 10.1016/j.ijheatmasstransfer.2022.123424 [85] KANG H L, TIAN Z F, CHEN G L, et al. Application of POD reduced-order algorithm on data-driven modeling of rod bundle[J]. Nuclear Engineering and Technology, 2022, 54(1): 36-48. doi: 10.1016/j.net.2021.07.010 [86] THUEREY N, WEIßENOW K, PRANTL L, et al. Deep learning methods for reynolds-averaged Navier-Stokes simulations of airfoil flows[J]. AIAA Journal, 2020, 58(1): 15-26. [87] BHATNAGAR S, AFSHAR Y, PAN S W, et al. Prediction of aerodynamic flow fields using convolutional neural networks[J]. Computational Mechanics, 2019, 64(2): 525-545. doi: 10.1007/s00466-019-01740-0 [88] MOHAN A T, GAITONDE D V. A deep learning based approach to reduced order modeling for turbulent flow control using LSTM neural networks[J]. arXiv preprint arXiv, 2018, 1804.09269. [89] GERMAN P, TANO M, FIORINA C, et al. GeN-ROM—an OpenFOAM®-based multiphysics reduced-order modeling framework for the analysis of Molten Salt Reactors[J]. Progress in Nuclear Energy, 2022, 146: 104148. doi: 10.1016/j.pnucene.2022.104148 [90] 邱亚松,白俊强,华俊. 基于本征正交分解和代理模型的流场预测方法[J]. 航空学报,2013, 34(6): 1249-1260. [91] YANG J, SUI X, HUANG Y P, et al. Assessment of reactor flow field prediction based on deep learning and model reduction[J]. Annals of Nuclear Energy, 2022, 179: 109367. doi: 10.1016/j.anucene.2022.109367 [92] GADALLA M, CIANFERRA M, TEZZELE M, et al. On the comparison of LES data-driven reduced order approaches for hydroacoustic analysis[J]. Computers & Fluids, 2021, 216: 104819. [93] MA W J, ZHANG J, YU J. Non-intrusive reduced order modeling for flowfield reconstruction based on residual neural network[J]. Acta Astronautica, 2021, 183: 346-362. doi: 10.1016/j.actaastro.2020.11.050 -






 下载:
下载: