全堆芯三维时空动力学中子输运程序SAAFCGSN应用研究

姜夺玉; 许鹏; 江新标; 胡田亮; 王立鹏; 曹璐; 李达

doi:10.13832/j.jnpe.2025.01.0013

全堆芯三维时空动力学中子输运程序SAAFCGSN应用研究

doi: 10.13832/j.jnpe.2025.01.0013

姜夺玉^{1, 2,},
许鹏¹,
江新标²,
胡田亮²,
王立鹏²,
曹璐²,
李达²

1.
火箭军工程大学，西安，710025
2.
西北核技术研究所强脉冲辐射环境模拟与效应国家重点实验室，西安，710024

基金项目: 国家自然科学基金项目（12205237，12275219）

详细信息

作者简介:
姜夺玉（1989—），男，助理研究员，博士研究生，现主要从事反应堆物理研究，E-mail: jcangyue@126.com

中图分类号: TL327
计量
- 文章访问数: 38
- HTML全文浏览量: 10
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-13
- 修回日期: 2024-06-10
- 刊出日期: 2025-02-15

Application Research on Whole-Core Three-Dimensional Space-Time Kinetics Neutron Transport Code SAAFCGSN

1.
Rocket Force University of Engineering, Xi’an, 710025, China
2.
State Key Laboratory of Intense Pulsed Radiation Simulation and Effect, Northwest Institute of Nuclear Technology, Xi’an, 710024, China

摘要

摘要: 当前为了应对新型先进小堆技术的发展，反应堆物理数值计算程序对三维全堆芯输运计算的要求不断提高。本文基于MOOSE平台开发了全堆芯三维时空动力学中子输运程序SAAFCGSN，该程序基于有限元方法实现空间变量离散，基于残差形式实现堆芯稳态、瞬态中子输运方程以及缓发中子先驱核方程的求解，采用JFNK方法避免直接求解Jacobin矩阵，从而提高计算速度，降低内存占用。为了检验程序的瞬态计算能力，本文使用经济发展与合作组织核能机构（OECD/NEA）C5G7-TD系列基准题验证了程序的可靠性，并与高保真确定论中子输运程序及蒙特卡罗程序模拟结果进行比较分析。研究表明，SAAFCGSN程序计算精度较高，可以有效处理控制棒尖齿效应，并得到详细的三维堆芯中子注量率分布，满足先进小堆的稳态及瞬态中子学计算需求。
- SAAFCGSN /
- MOOSE平台 /
- 时空动力学 /
- C5G7-TD基准题 /
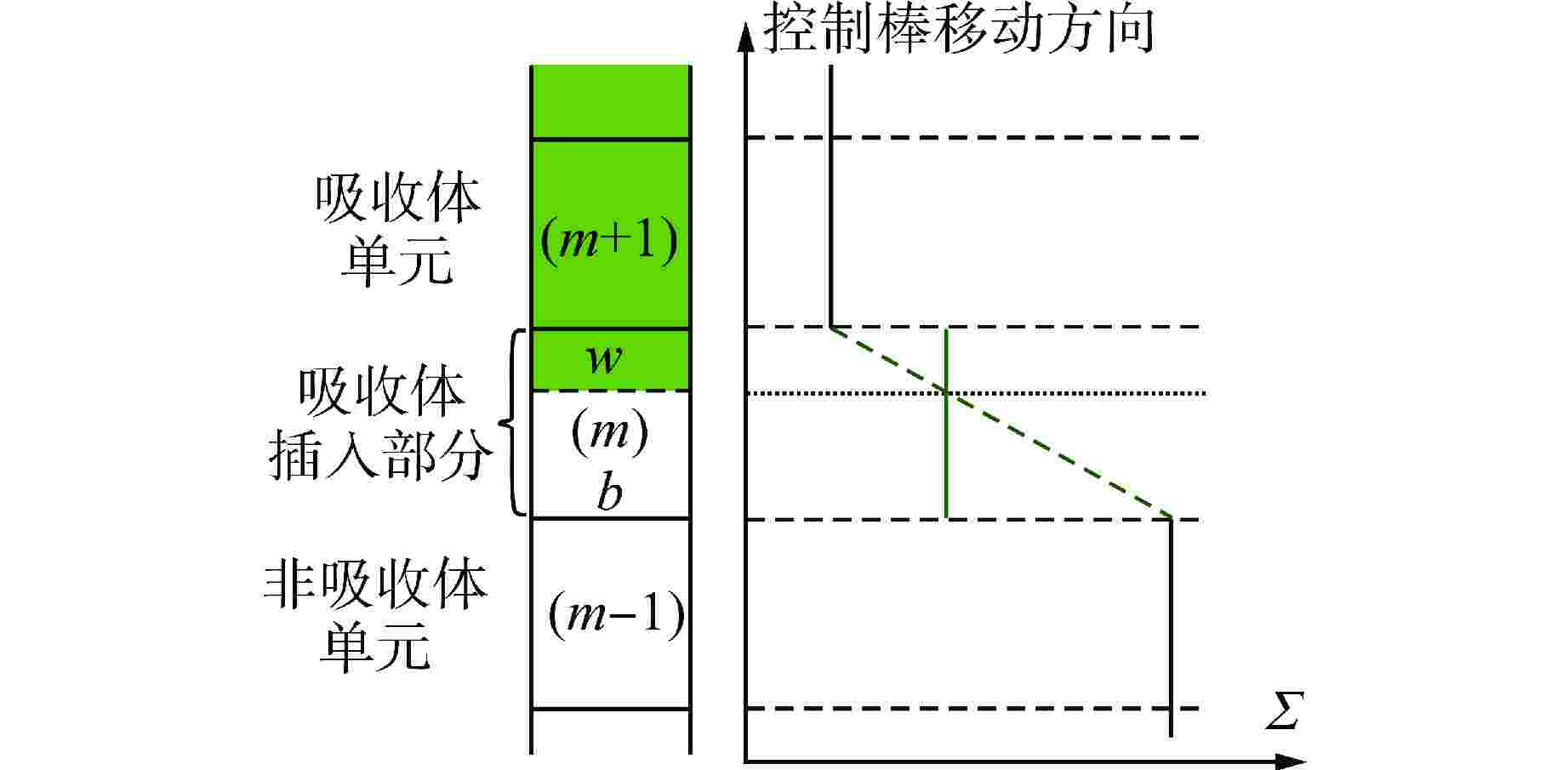
- 尖齿效应
Abstract: In response to the evolving demands of advanced small reactor technologies, there is an increasing requirement for three-dimensional whole core transport calculations in reactor physics numerical simulation codes. This paper presents the development of a three-dimensional space-time kinetics neutron transport code, SAAFCGSN, based on the MOOSE platform. The code implements spatial variable discretization using the finite element method, and solves the steady-state and transient neutron transport equations as well as the delayed neutron precursor equations using a residual form approach. The Jacobian-Free Newton-Krylov (JFNK) method is employed to avoid the direct computation of the Jacobian matrix, thereby enhancing computational speed and reducing memory usage. To evaluate the transient computational capability of the code, we validated its reliability using the OECD/NEA C5G7-TD benchmark series and conducted a comparative analysis with high-fidelity deterministic neutron transport codes and Monte Carlo simulations. The study demonstrates that the SAAFCGSN code achieves high computational accuracy, effectively manages the cusping effect of control rods, and obtains detailed neutron flux distributions within the three-dimensional core. It meets the steady-state and transient neutronic calculation requirements for advanced small reactors.
- SAAFCGSN /
- MOOSE platform /
- Space-time kinetics /
- C5G7-TD benchmark question /
- Cusping effect

HTML全文

图 1 瞬态求解流程图

Figure 1. Flowchart of Transient Solving

下载: 全尺寸图片幻灯片

图 2 控制棒尖齿效应处理模型

Figure 2. Model of Control Rod Cusping Treatment

下载: 全尺寸图片幻灯片

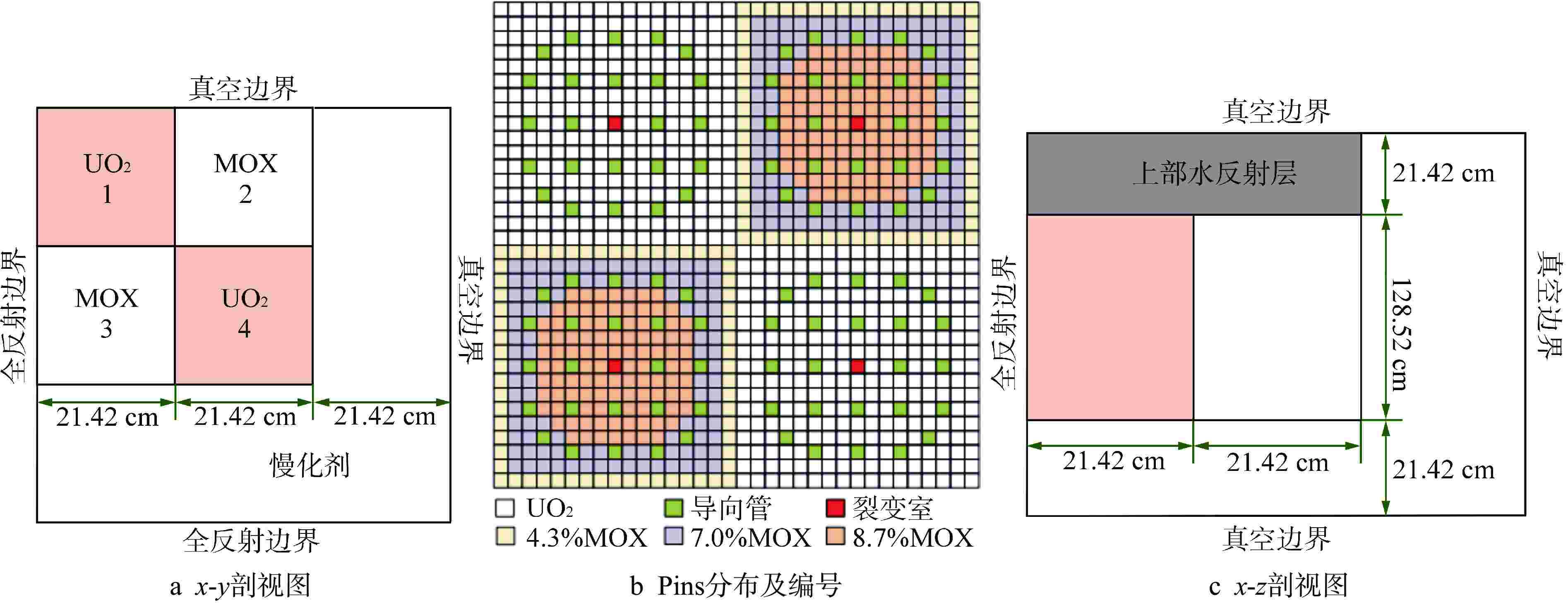
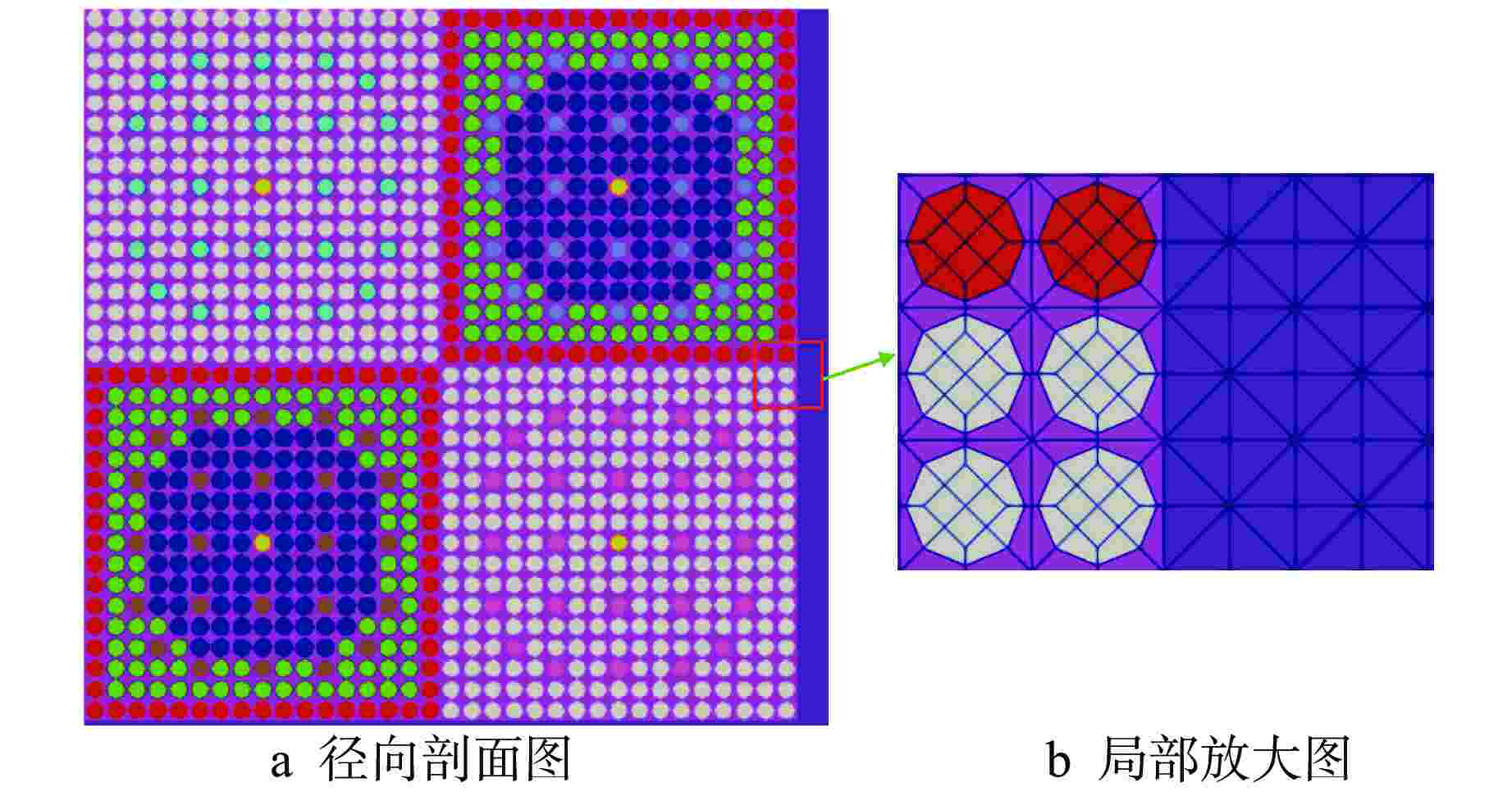
图 3 C5G7-TD堆芯结构图^[19]

Figure 3. C5G7-TD Core Structure Diagram

下载: 全尺寸图片幻灯片

图 4 C5G7-TD二维问题反应性引入方式

δ—初始密度比例的峰值

Figure 4. Reactivity Introduction Mode of C5G7-TD 2D Benchmark

下载: 全尺寸图片幻灯片

图 5 C5G7-TD三维问题控制棒拔插及慢化剂改变过程

Figure 5. Process of Control Rod Movement and Moderator Density Change of C5G7-TD 3D Benchmark

下载: 全尺寸图片幻灯片

图 6 C5G7-TD网格剖分

Figure 6. Meshing for C5G7-TD

下载: 全尺寸图片幻灯片

图 7 C5G7-TD稳态裂变率及缓发中子先驱核浓度分布

Figure 7. Steady-state Fission Rate and Delayed Neutron Precursor Distribution of C5G7-TD

下载: 全尺寸图片幻灯片

图 8 不同时间步长堆芯裂变率相对偏差

Figure 8. Relative Error of Core Fission Rate with Different Time Steps

下载: 全尺寸图片幻灯片

图 9 TD0/TD2/TD3/TD5的瞬态计算结果

Figure 9. Transient Calculation Results of TD0/TD2/TD3/TD5

下载: 全尺寸图片幻灯片

图 10 TD1的瞬态计算结果误差分析

Figure 10. Error Analysis of Transient Calculation Results of TD1

下载: 全尺寸图片幻灯片

图 11 TD4的瞬态计算结果误差分析

Figure 11. Error Analysis of Transient Calculation Results of TD4

下载: 全尺寸图片幻灯片

图 12 TD4-5控制棒尖齿效应

Figure 12. Control Rod Cusping Effect of TD4-5

下载: 全尺寸图片幻灯片

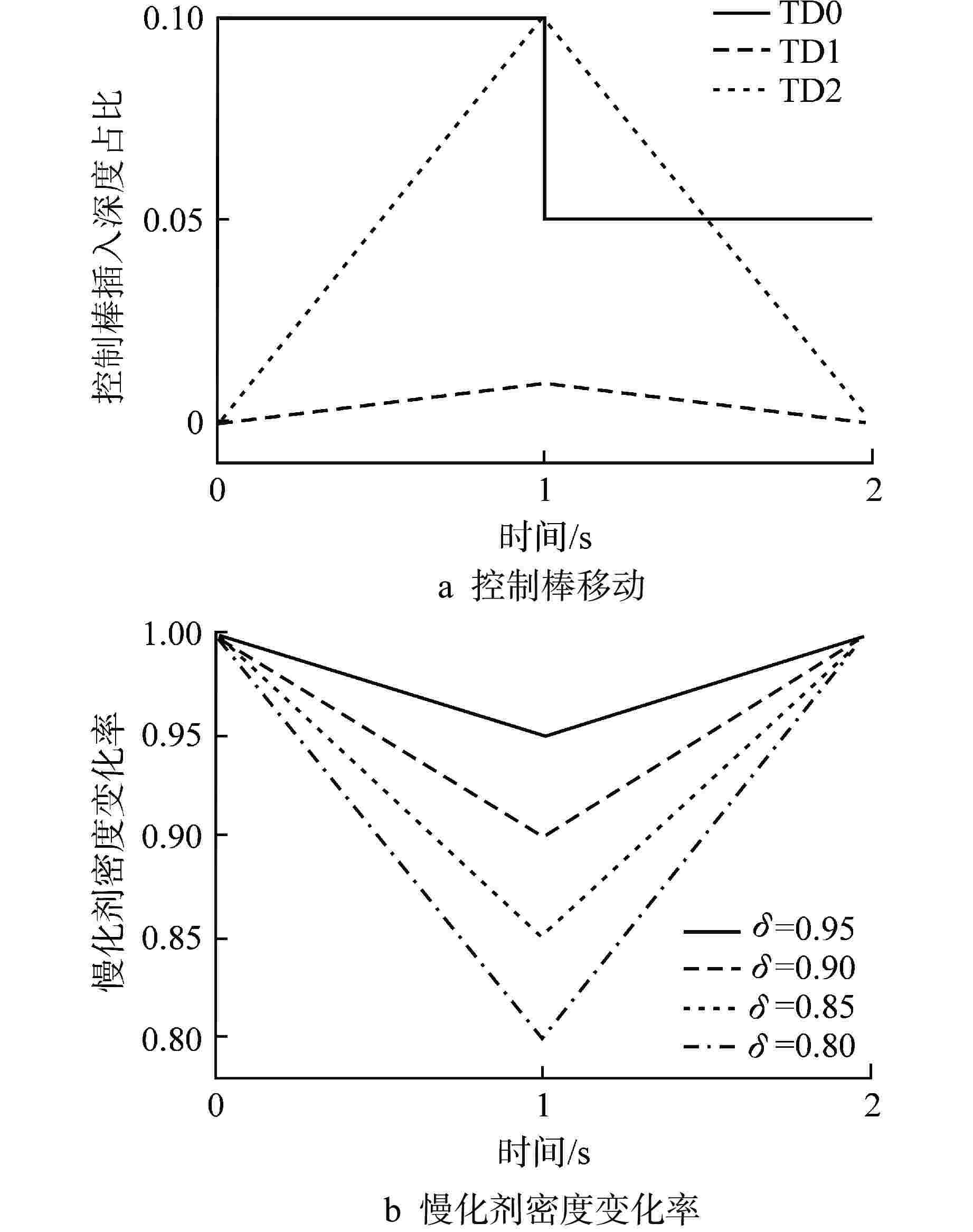
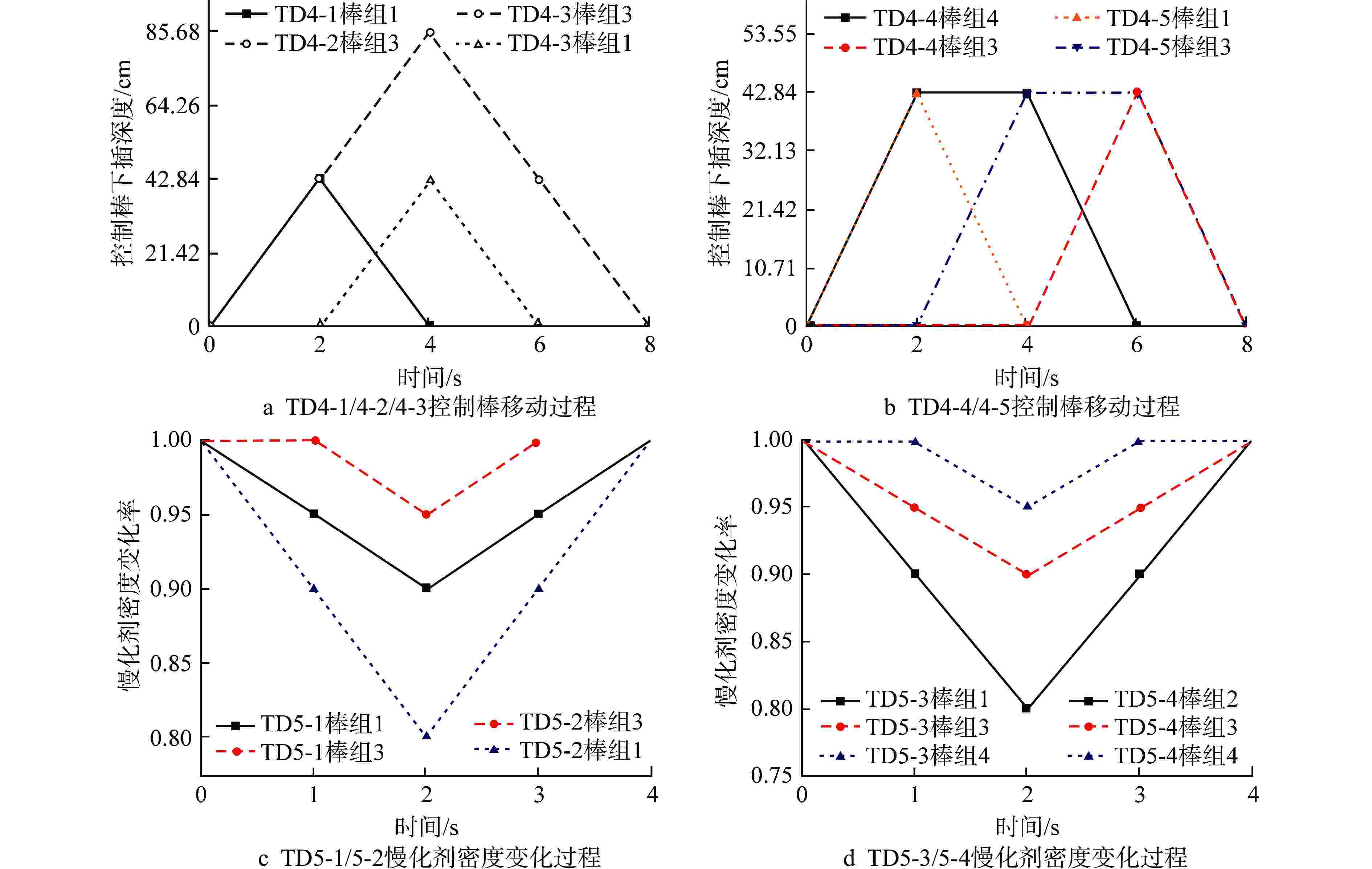
表 1 控制棒组移动方案

Table 1. Movement Scheme for Control Rod Groups

方案	TD0	TD1	TD2
1	棒组1	棒组1	棒组1
2	棒组3	棒组3	棒组3
3	棒组4	棒组4	棒组4
4	棒组1-3-4	棒组1-3-4
5	棒组1-2-3-4	棒组1-2-3-4

下载: 导出CSV

表 2 C5G7-TD基准题k_eff计算结果

Table 2. k_eff Calculation Results of C5G7-TD

程序	二维		三维
程序	k_eff	相对偏差/%	k_eff	相对偏差/%
OpenMC	1.18644±0.00005		1.16532±0.00004
PANDAS-MOC	1.186314	−0.011	1.165119	−0.017
NECP-X	1.18695	0.043	1.16580	0.041
Rattlesnake	1.183937	−0.211	1.162431	−0.248
McCARD	1.18107	−0.453
SAAFCGSN	1.184630	−0.153	1.164433	−0.076

下载: 导出CSV

表 3 C5G7-TD问题时间步长设置

Table 3. Time Steps Setting of C5G7-TD

TD0/TD1/TD2/TD3		TD4		TD5
时间/s	步长/s	时间/s	步长/s	时间/s	步长/s
0~2.0	0.025	0~0.1	0.025	0~0.1	0.025
2.0~2.5	0.05	0.1~0.2	0.1	0.10~0.25	0.05
2.5~3.0	0.1	0.2~4.0	0.2	0.25~4.00	0.25
3.0~5.0	0.5	4~10	0.5	4~6	0.5

下载: 导出CSV

表 4 TD0-1/2瞬态裂变率与MPACT结果对比

Table 4. Comparison of Transient Fission Rate Results between TD0-1/2 and MPACT

时间/s	MPACT		本文工作		相对偏差/%
时间/s	TD0-1	TD0-2	TD0-1	TD0-2	TD0-1	TD0-2
0.1	0.144	0.557	0.14671	0.57885	−1.85	−3.77
0.5	0.128	0.525	0.13052	0.54759	−1.93	−4.13
1.0	0.115	0.497	0.11711	0.51961	−1.80	−4.35
1.5	0.174	0.606	0.17826	0.62826	−2.39	−3.54
2.0	0.163	0.592	0.16684	0.61457	−2.30	−3.67
2.5	0.714	0.858	0.71599	0.86674	−0.28	−1.01
3.0	0.740	0.871	0.74158	0.87850	−0.21	−0.85
3.5	0.757	0.880	0.75730	0.88579	−0.04	−0.65
4.0	0.770	0.886	0.76958	0.89150	0.05	−0.62
4.5	0.780	0.891	0.77958	0.89616	0.05	−0.58
5.0	0.788	0.895	0.78799	0.90008	0	−0.56

下载: 导出CSV

参考文献(26)

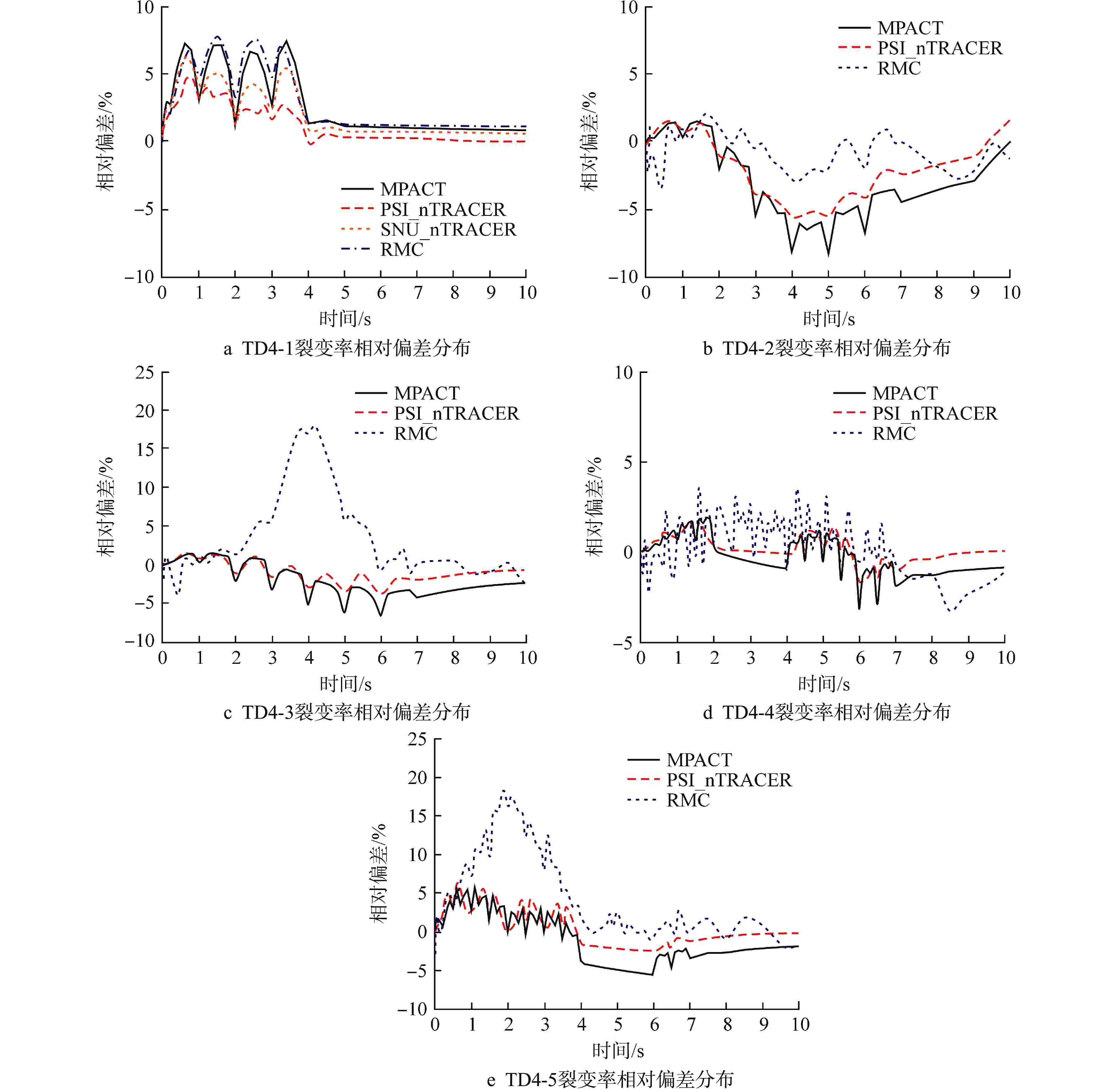
[1]	吴宏春,杨红义,曹良志,等. 金属冷却快堆关键分析软件的现状与展望[J]. 现代应用物理,2021, 12(1): 010201.
[2]	卢琳龙,李兵,高辉. 含氢反射层对金属活性区快中子脉冲反应堆特性参数的影响[J]. 现代应用物理,2022, 13(2): 020205.
[3]	CARLSON B G. Solution of the transport equation by S_n approximations: LA-1599[R]. Los Alamos: Los Alamos Scientific Laboratory, 1955.
[4]	STACEY W M. Nuclear reactor physics[M]. 2nd ed. Weinheim: WILEY-VCH Verlag GmbH & Co. KGaA, 2007: 338-353.
[5]	JIANG D Y, XU P, HU T L, et al. Coupled Monte Carlo and thermal-hydraulics modeling for the three-dimensional steady-state analysis of the Xi’an Pulsed Reactor[J]. Energies, 2023, 16(16): 6046. doi: 10.3390/en16166046
[6]	MOREL J E, MCGHEE J M. A self-adjoint angular flux equation[J]. Nuclear Science and Engineering, 1999, 132(3): 312-325. doi: 10.13182/NSE132-312
[7]	POMRANING G C, CLARK JR M. The variational method applied to the monoenergetic Boltzmann equation. Part II[J]. Nuclear Science and Engineering, 1963, 16(2): 155-164. doi: 10.13182/NSE63-A26495
[8]	ACKROYD R T. Least-squares derivation of extremum and weighted-residual methods for equations of reactor physics—I. The first-order Boltzmann equation and a first-order initial-value equation[J]. Annals of Nuclear Energy, 1983, 10(2): 65-99. doi: 10.1016/0306-4549(83)90011-7
[9]	LISCUM-POWELL J L. Finite element numerical solution of a self-adjoint transport equation for coupled electron-photon problems[D]. New Mexico: The University of New Mexico, 2000.
[10]	曹良志,吴宏春,周永强. 非结构几何下二阶自共轭中子输运方程中的简化球谐函数方法研究[J]. 核动力工程,2006, 27(3): 6-10. doi: 10.3969/j.issn.0258-0926.2006.03.002
[11]	叶青,吴宏春. R-Z几何中子输运方程的球谐函数方法[J]. 核动力工程,2008, 29(4): 19-23.
[12]	SCHUNERT S, WANG Y Q, MARTINEAU R, et al. A new mathematical adjoint for the modified SAAF-S_N equations[J]. Annals of Nuclear Energy, 2015, 75: 340-352. doi: 10.1016/j.anucene.2014.08.028
[13]	WANG Y Q, DEHART M D, GASTON D R, et al. Convergence study of Rattlesnake solutions for the two-dimensional C5G7 MOX benchmark[C]//Proceedings of Joint International Conference on Mathematics and Computation. Idaho Falls: Idaho National Lab. , 2015.
[14]	WANG Y Q, SCHUNERT S, LABOURÉ V. Rattlesnake theory manual: INL/EXT-17-42103[R]. Idaho Falls: Idaho National Laboratory, 2018.
[15]	LATIMER C, KÓPHÁZI J, EATON M D, et al. A geometry conforming isogeometric method for the self-adjoint angular flux (SAAF) form of the neutron transport equation with a discrete ordinate (S_N) angular discretisation[J]. Annals of Nuclear Energy, 2020, 136: 107049. doi: 10.1016/j.anucene.2019.107049
[16]	GIUDICELLI G, LINDSAY A, HARBOUR L, et al. 3.0 - MOOSE: enabling massively parallel multiphysics simulations[J]. SoftwareX, 2024, 26: 101690. doi: 10.1016/j.softx.2024.101690
[17]	KNOLL D A. KEYES D E. Jacobian-free Newton-Krylov methods: a survey of approaches and applications[J]. Journal of Computational Physics, 2004, 193(2): 357-397. doi: 10.1016/j.jcp.2003.08.010
[18]	JOO H S. Resolution of the control rod cusping problem for nodal methods[D]. Cambridge: Massachusetts Institute of Technology, 1984.
[19]	HOU J, IVANOV K N, BOYARINOV V F, et al. OECD/NEA benchmark for time-dependent neutron transport calculations without spatial homogenization[J]. Nuclear Engineering and Design, 2017, 317: 177-189. doi: 10.1016/j.nucengdes.2017.02.008
[20]	JIANG D Y, XU P, HU T L, et al. Transient multi-physics coupling analysis of the Xi'an Pulsed Reactor under pulsed condition[J]. Annals of Nuclear Energy, 2024, 200: 110379. doi: 10.1016/j.anucene.2024.110379
[21]	TAO S J, XU Y L. Neutron transport analysis of C5G7-TD benchmark with PANDAS-MOC[J]. Annals of Nuclear Energy, 2022, 169: 108966. doi: 10.1016/j.anucene.2022.108966
[22]	王博,刘宙宇,陈军,等. 基于NECP-X程序的C5G7-TD系列基准题的计算与分析[J]. 核动力工程,2020, 41(3): 24-30.
[23]	张旻婉,刘宙宇,温兴坚,等. 用NECP-X程序计算与分析VERA 9^#基准题[J]. 现代应用物理,2021, 12(1): 010212.
[24]	DEHART M D, MAUSOLFF Z, WEEMS Z, et al. Preliminary results for the OECD/NEA time dependent benchmark using Rattlesnake, Rattlesnake-IQS and TDKENO: INL/EXT-16-39723[R]. Idaho Falls: Idaho National Laboratory, 2016.
[25]	GUO X Y, SHANG X T, SONG J, et al. Kinetic methods in Monte Carlo code RMC and its implementation to C5G7-TD benchmark[J]. Annals of Nuclear Energy, 2021, 151: 107864. doi: 10.1016/j.anucene.2020.107864
[26]	SHEN Q C, WANG Y R, JABAAY D, et al. Transient analysis of C5G7-TD benchmark with MPACT[J]. Annals of Nuclear Energy, 2019, 125: 107-120. doi: 10.1016/j.anucene.2018.10.049