Investigation on the Flow and Heat Transfer Characteristics of Liquid Lead Cross-flow Tube Bundle under Cooling Conditions
-
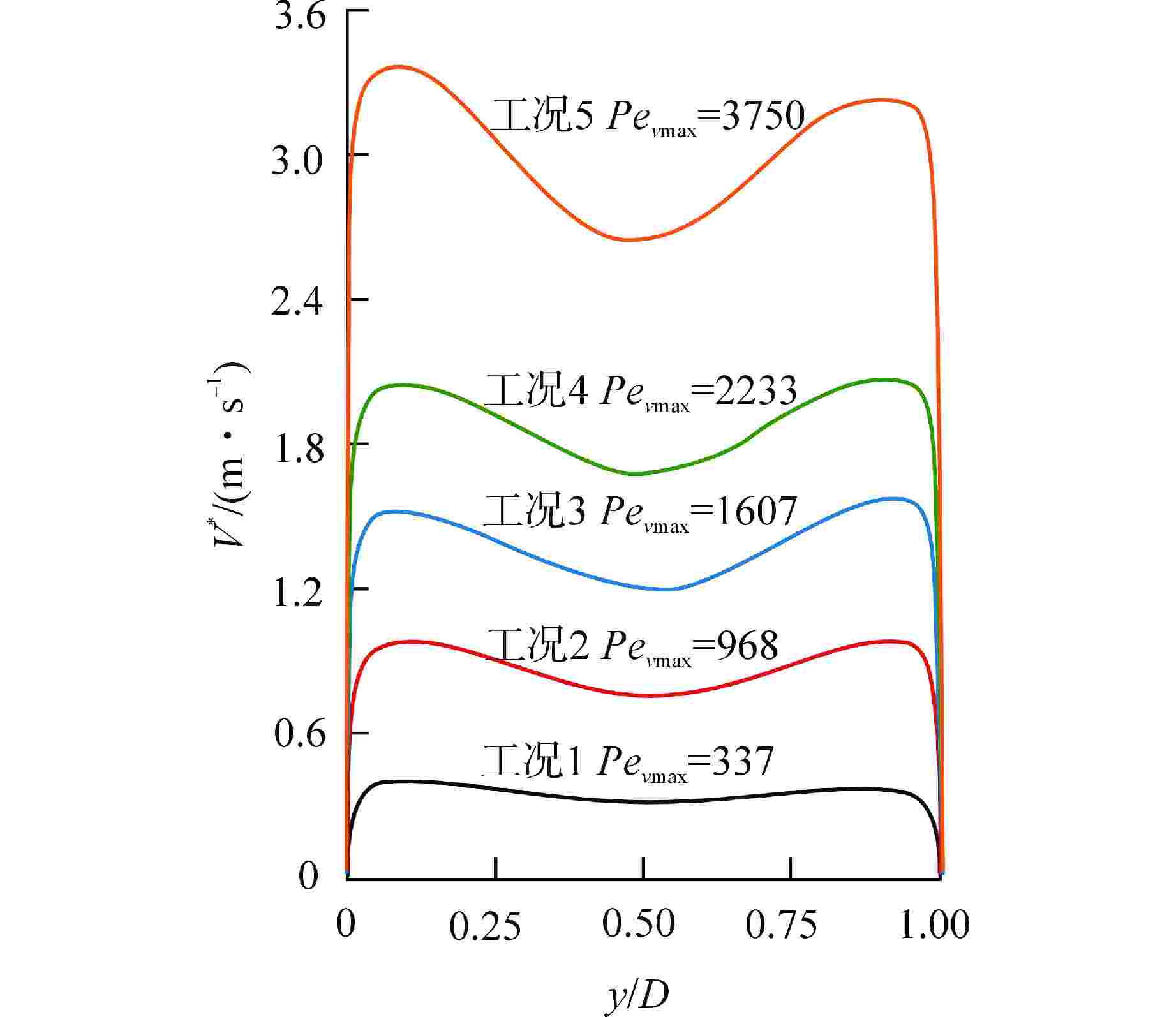
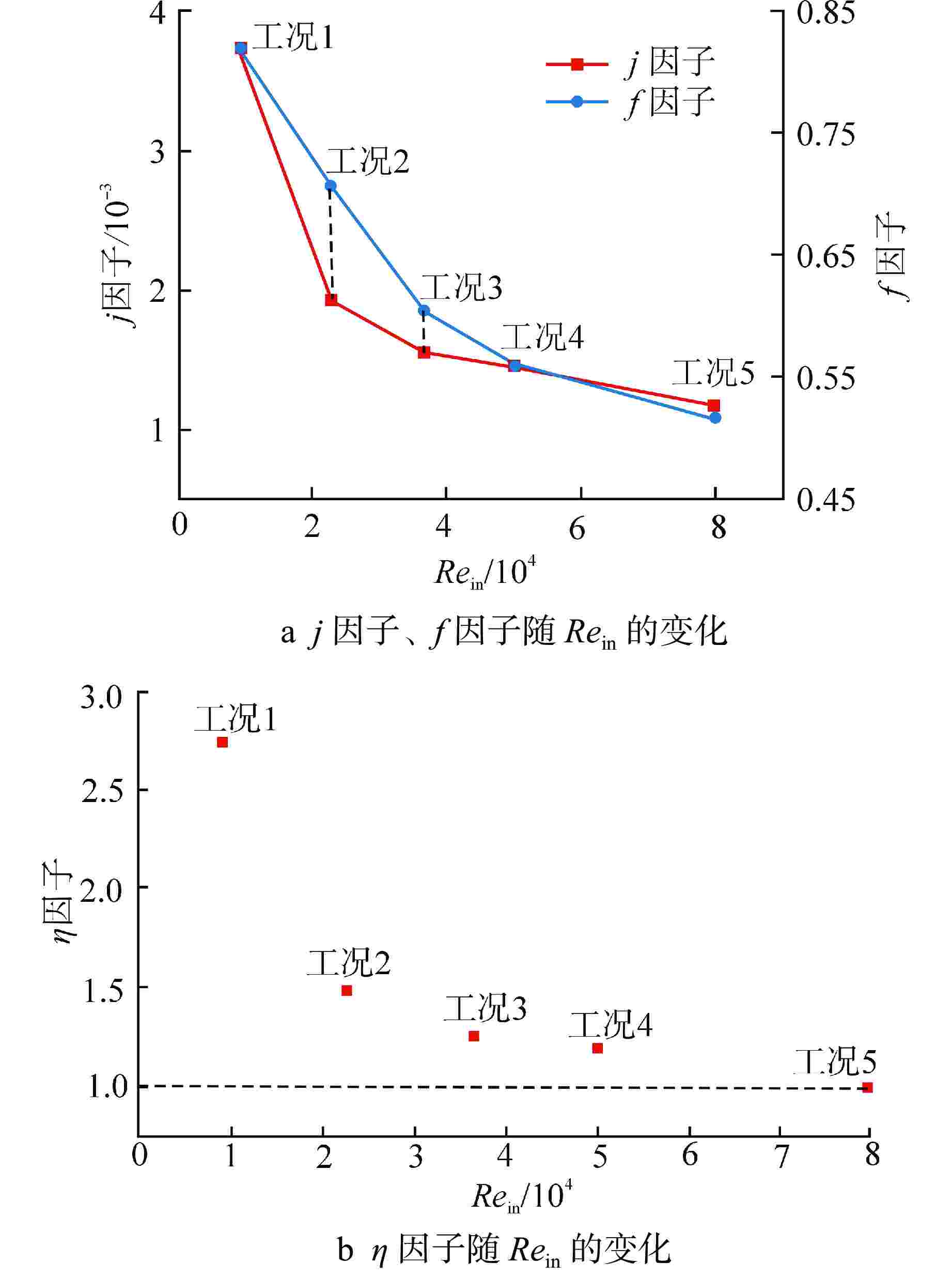
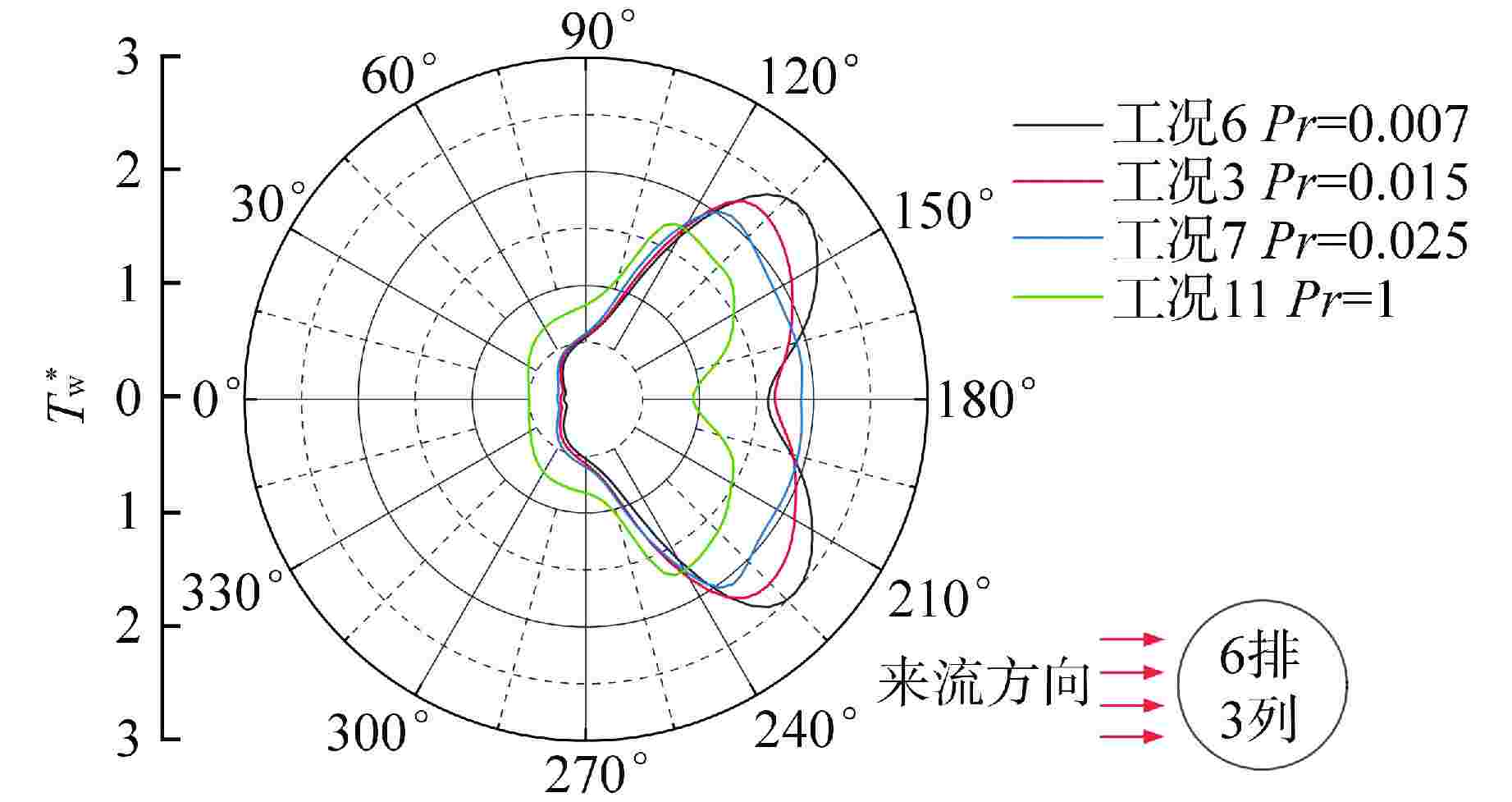
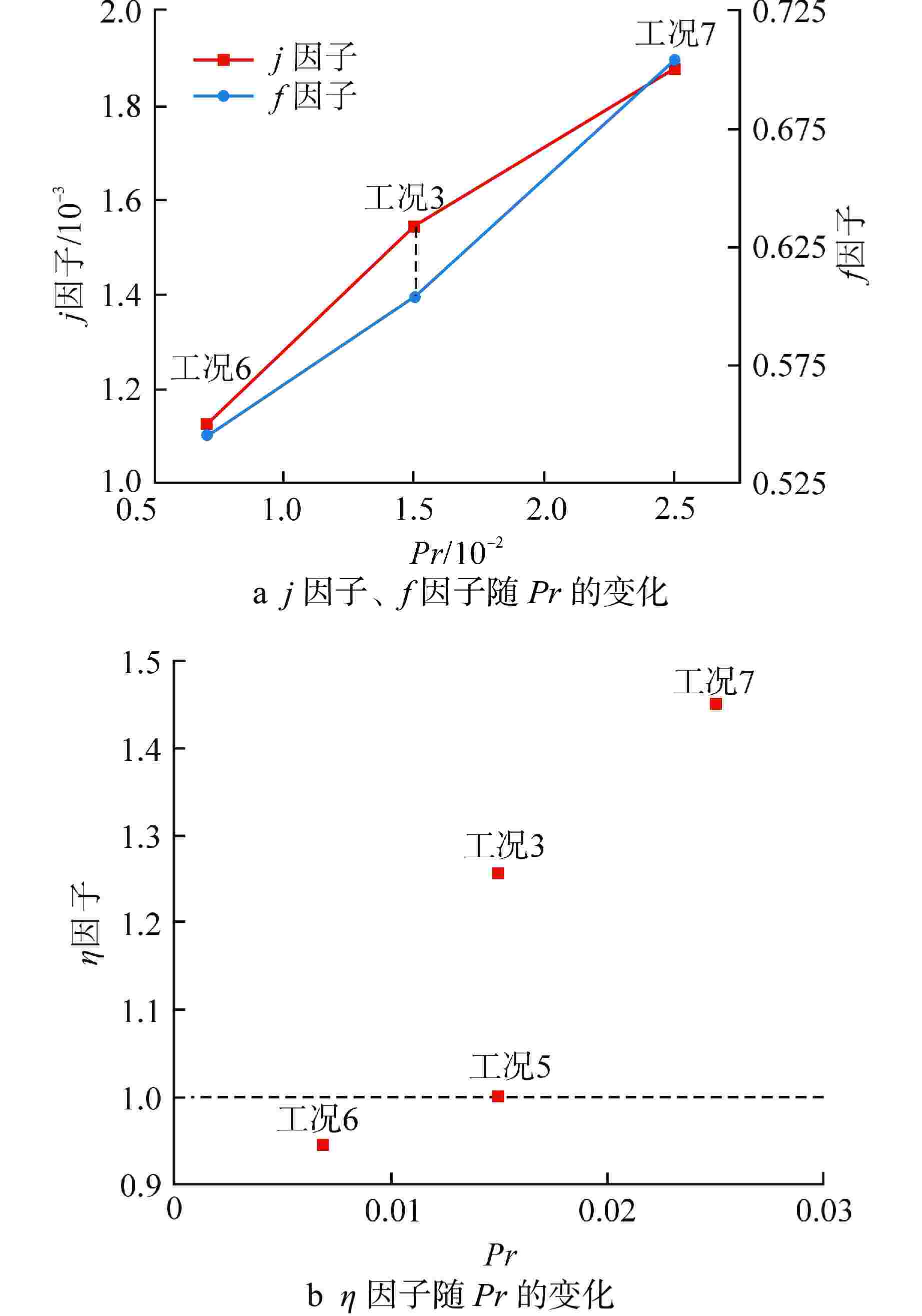
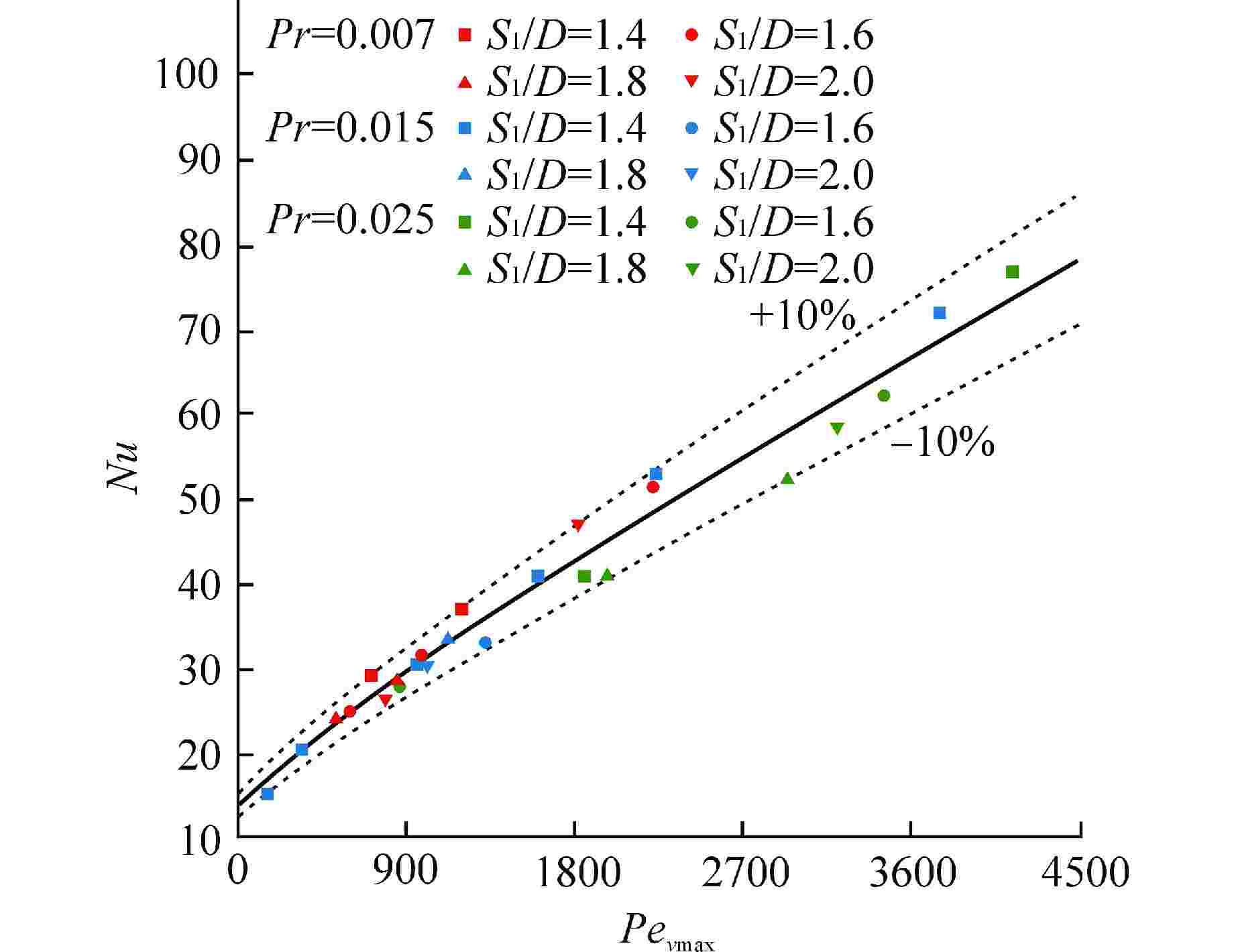
摘要: 液态金属冷却剂在主换热器内的流动传热特性对铅冷快堆的高效安全经济运行具有重要影响。本研究针对螺旋盘管式换热器中管束布置特征,建立了液态铅横流管束二维分析模型,对比分析了适用于液态铅横流管束流动的湍流普朗特数模型,采用数值模拟方法研究了液态铅横流冲刷换热管束的流动传热特性。结果表明,随着入口雷诺数的增大,液态铅在管间的时均速度分布曲线下凹程度增加,回流区内无量纲壁温的差异增大,并且涡旋对管壁180°附近区域的扰动增强。液态铅在横掠管束时的综合流动换热性能与螺旋盘管横向节径比呈正相关关系,与进口雷诺数呈负相关关系。基于数值模拟研究结果提出了液态铅横流错排管束的传热关联式,其预测误差在10%以内。Abstract: The flow and heat transfer characteristics of liquid metal coolant in the primary heat exchanger are of great importance to the economic and safe operation of lead-cooled fast reactor. According to the arrangement characteristics of tube bundle in a spiral coil heat exchanger, the present study established a two-dimensional analysis model for liquid lead cross-flow tube bundle. The turbulent Prandtl number model suitable for the flow of liquid lead cross-flow tube bundle is compared and analyzed, and the flow and heat transfer characteristics of liquid lead cross-flow scouring heat exchanger tube bundle are studied by numerical simulation. The results show that with the increase of inlet Reynolds number, the concave degree of the time-average velocity distribution curve of liquid lead among tubes increases, and the difference of dimensionless wall temperature enlarges in the return area, while the vortex disturbance is enhanced to the area around 180° of the tube walls. The comprehensive flow and heat transfer performance of liquid lead transversally scouring tube bundles has a positive correlation with the transverse pitch diameter ratio of the spiral coil and a negative correlation with the inlet Reynolds number. Based on the numerical simulation, the heat transfer correlation of liquid lead transversally scouring tube bundles is proposed, and its prediction error is less than 10%.
-
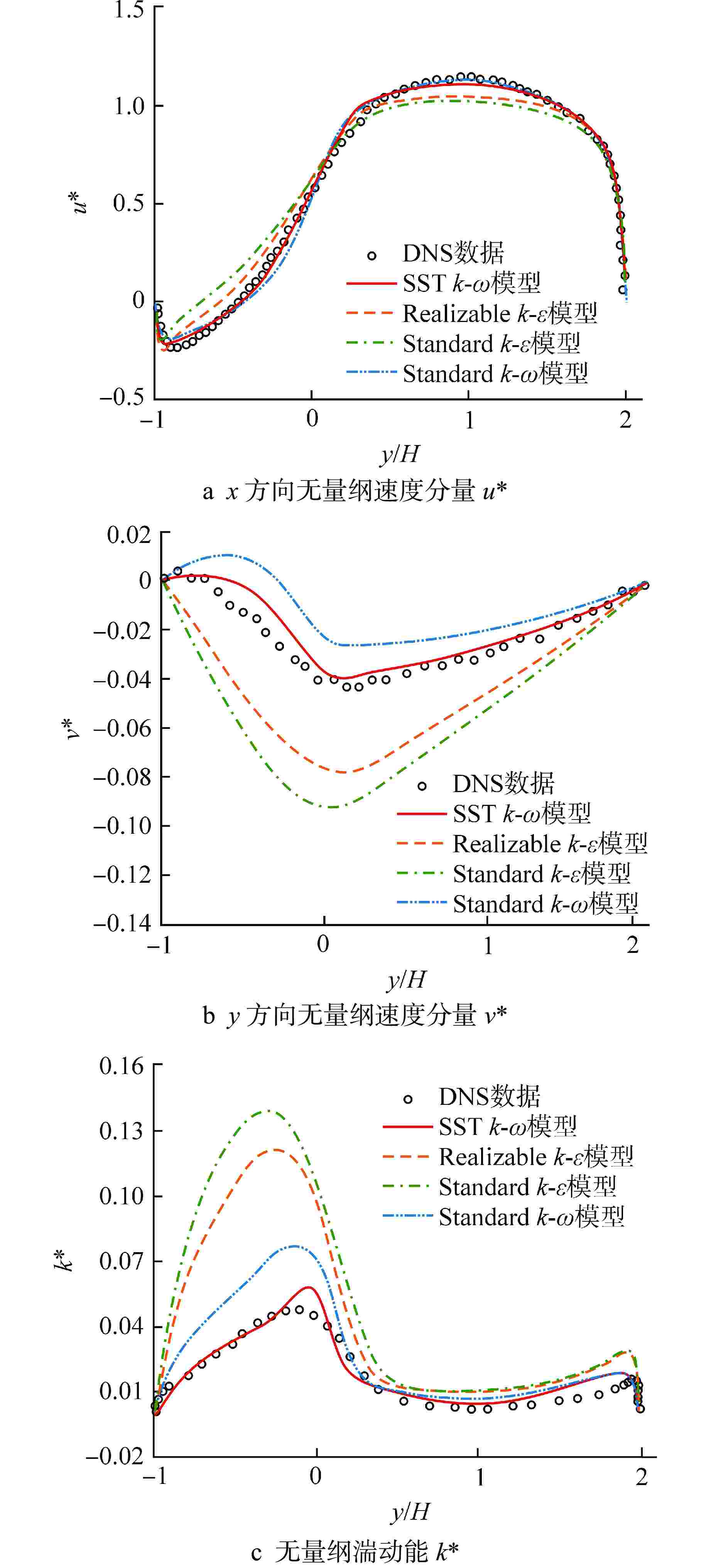
图 7 Kalish实验[24]几何模型示意图
Figure 7. Schematic Diagram of the Kalish Test Geometry Model
表 1 湍流普朗特数模型汇总
Table 1. Summary of Turbulence Prandtl Number Models
分类 提出者 模型 第一类湍流普朗特数模型 Aoki(1963)[10] $ Pr_{\text{t}}^{ - 1} = 0.014R{e^{0.45}}P{r^{0.2}}\left[ {1 - \exp \left( { - \dfrac{1}{{0.014R{e^{0.45}}P{r^{0.2}}}}} \right)} \right] $ (7) Reynolds(1975)[11] $P{r_{\text{t}}} = \left( {1 + 100P{e^{ - 0.5}}} \right)\left( {\dfrac{1}{{1 + 120R{e^{ - 0.5}}}} - 0.15} \right)$ (8) Jiacha&Rieke(1979)[12] $P{r_{\text{t}}} = 0.9 + \dfrac{{182.4}}{{PrR{e^{0.888}}}}$ (9) Cheng&Tak(2006)[13] $ \begin{gathered} P{r_{\text{t}}} = \left\{ \begin{array}{*{20}{l}} 4.12 & {{ Pe}} \leqslant 1000 \\ \dfrac{{0.01Pe}}{{{{\left[ {0.018P{e^{0.8}} - \left( {7.0 - A} \right)} \right]}^{1.25}}}}{\text{ }} & 1000{{ < Pe}} \leqslant 6000 \\ \end{array} \right. \\ \;\;\; A = \left\{ \begin{array}{*{20}{l}} 5.4 - 9 \times {10^{ - 4}}{{Pe }} & 1000 < Pe \leqslant 2000 \\ 3.6{\text{ }} & 2000 < Pe \leqslant 6000 \\ \end{array} \right. \\ \end{gathered} $ (10) Taler(2017)[14] $Pr_t^{ - 1} = 0.01592R{e^{0.45}}P{r^{0.2}}\left[ {1 - \exp \left( { - \dfrac{1}{{0.01592R{e^{0.45}}P{r^{0.2}}}}} \right)} \right]$ (11) 第二类湍流普朗特数模型 Kays&Crawford(1993)[15] $Pr_{\text{t}}^{ - 1} = 0.5882 + 0.228\dfrac{{{\varepsilon _M}}}{\nu } - 0.0441{\left( {\dfrac{{{\varepsilon _M}}}{\nu }} \right)^2}\left[ {1 - \exp \left( {\dfrac{{ - 5.165}}{{{{{\varepsilon _M}} \mathord{\left/ {\vphantom {{{\varepsilon _M}} \nu }} \right. } \nu }}}} \right)} \right]$ (12) Kays(1994)[16] $P{r_{\text{t}}} = 0.85 + \dfrac{2}{{P{e_{\text{t}}}}},{\text{ }}\quad P{e_{\text{t}}} = Pr\dfrac{{{\varepsilon _M}}}{\nu }$ (13) Weigand(1997)[17] $\begin{gathered} Pr_{\text{t}}^{ - 1} = \dfrac{1}{{2P{r_{{\text{t}}\infty }}}} + C \cdot P{e_{\text{t}}}\sqrt {\dfrac{1}{{P{r_{{\text{t}}\infty }}}}} - {\left( {C \cdot P{e_{\text{t}}}} \right)^2}\left[ {1 - \exp \left( { - \dfrac{1}{{CP{e_{\text{t}}}\sqrt {P{r_{{\text{t}}\infty }}} }}} \right)} \right] \\ P{r_{{\text{t}}\infty }} = 0.85 + \dfrac{{100}}{{PrR{e^{0.888}}}} \\ \end{gathered} $ (14) Lei(2022)[18] $P{r_{\mathrm{t}}} = 0.85 + \dfrac{{2.5}}{{P{e_{\mathrm{t}}}}},{\text{ }} \quad P{e_{\mathrm{t}}} = Pr\dfrac{{{\varepsilon _M}}}{\nu }$ (15) Pet—以Prt为基准计算的贝克莱数;Prt∞—无穷远处来流的湍流普朗特数 表 2 冷却条件下液态铅横流管束数值计算工况
Table 2. Numerical Calculation of Liquid Lead Cross-flow Tube Bundle under Cooling Condition
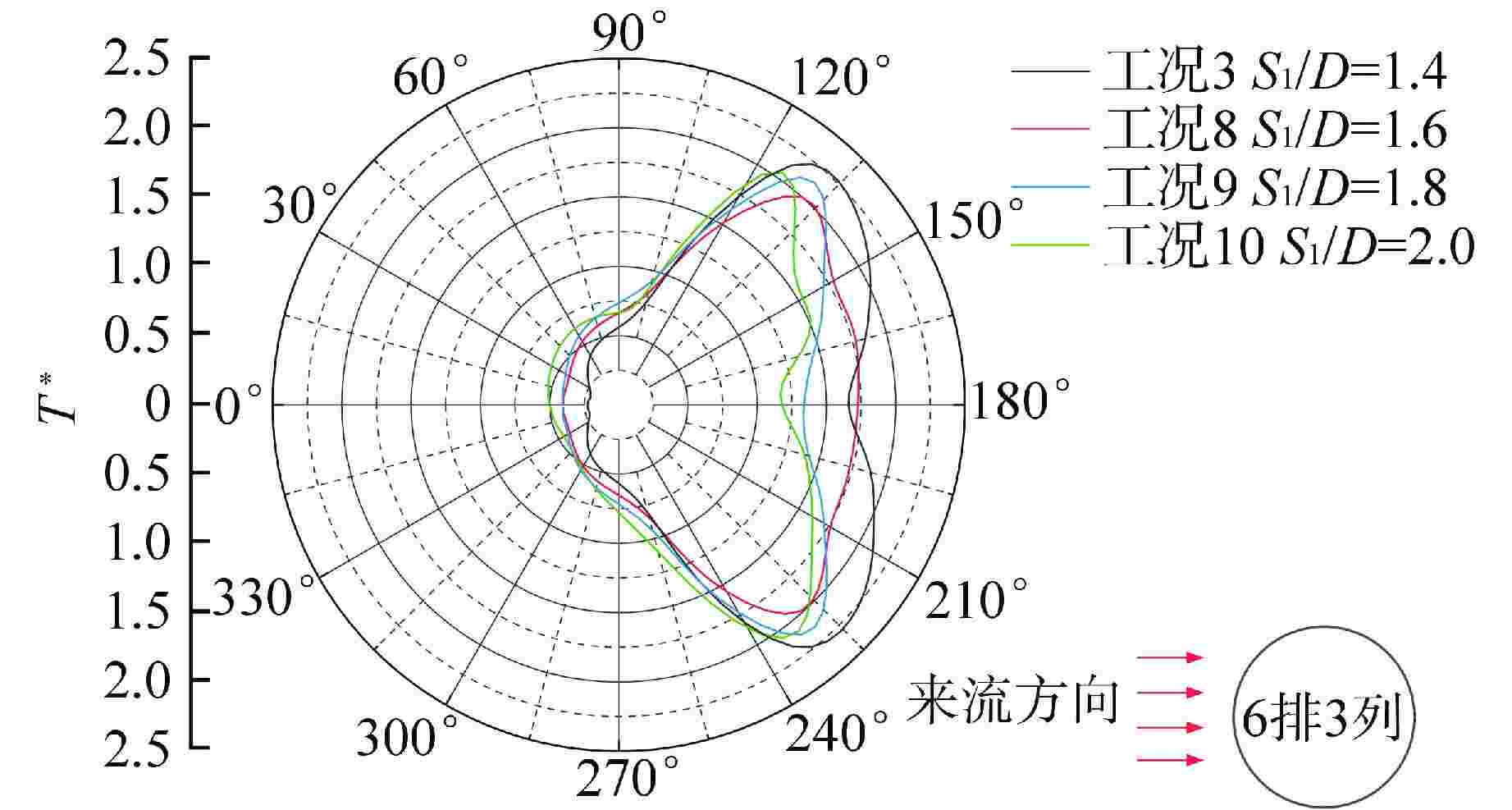
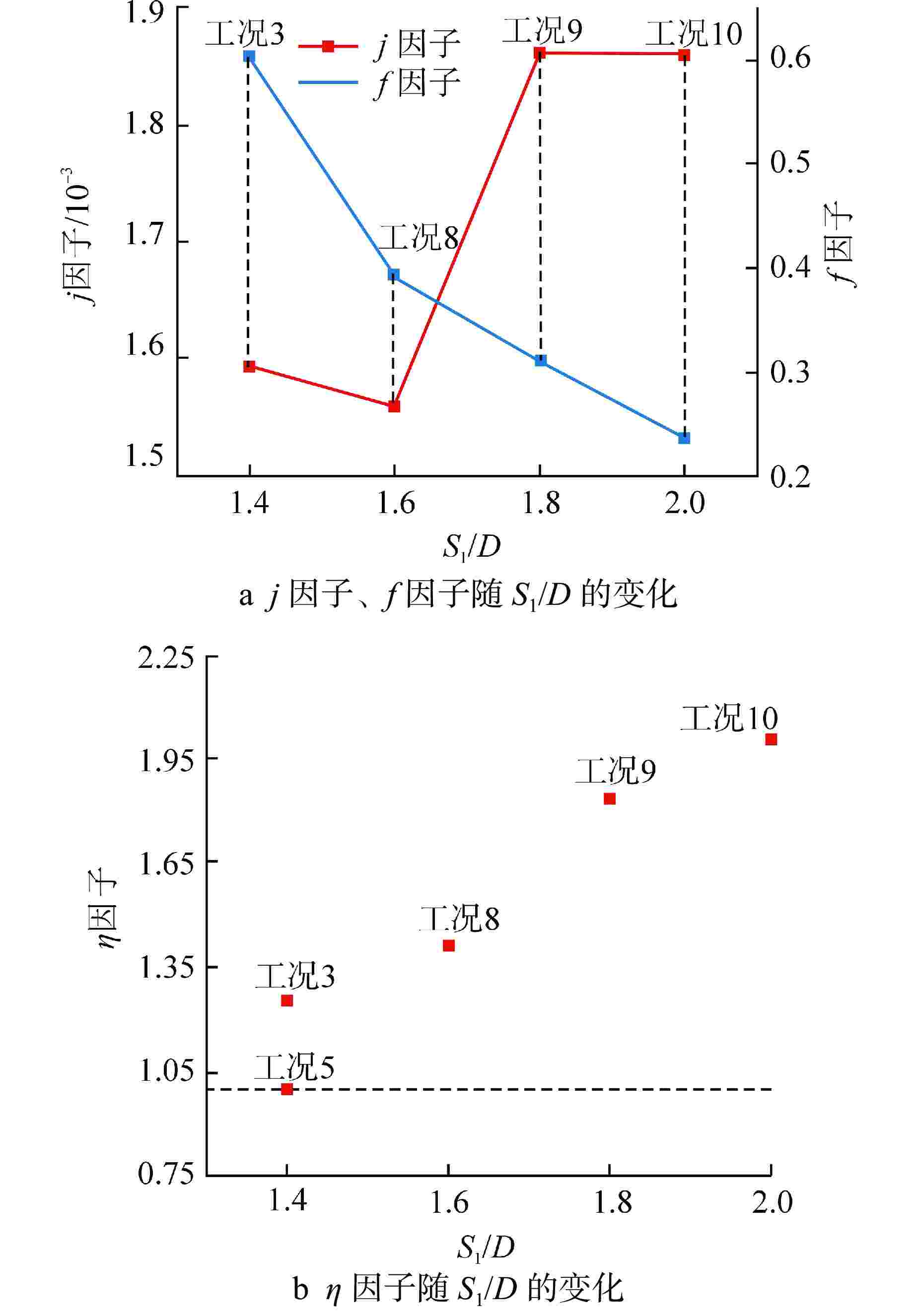
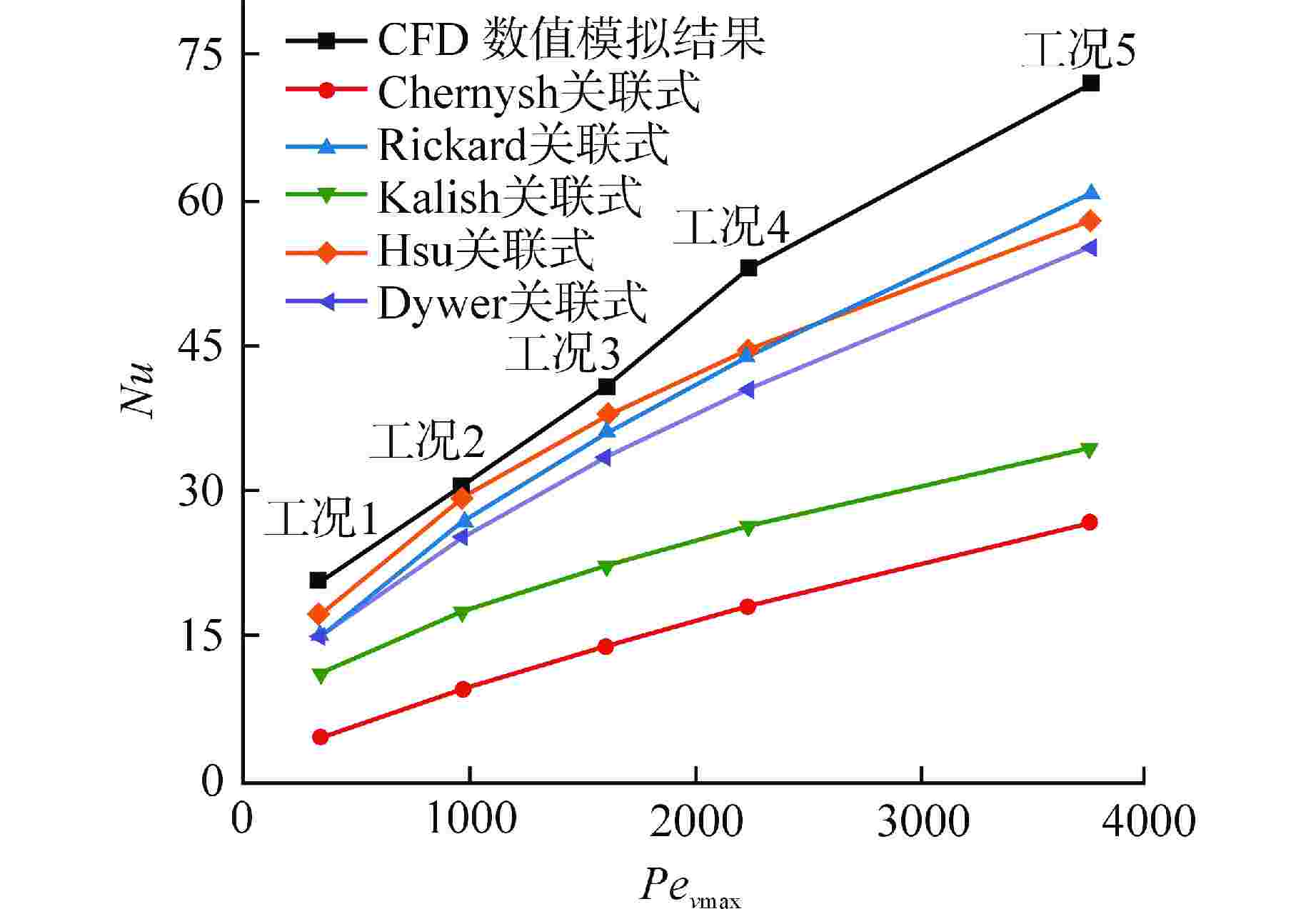
工况 工质 Rein Pr qw/(W·m−2) S1/D Revmax Nu 1 液态铅 9.13×103 0.015 −3×105 1.4 2.25×104 20.67 2 液态铅 2.28×104 0.015 −5×105 1.4 6.45×104 30.63 3 液态铅 3.65×104 0.015 −8×105 1.4 1.07×105 40.82 4 液态铅 5.00×104 0.015 −2×106 1.4 1.49×105 53.00 5 液态铅 8.00×104 0.015 −2×106 1.4 2.50×105 71.99 6 液态铅 1.20×105 0.007 −8×105 1.4 1.72×105 36.98 7 液态铅 1.20×105 0.025 −8×105 1.4 7.44×104 40.93 8 液态铅 1.20×105 0.015 −8×105 1.6 8.86×104 32.98 9 液态铅 1.20×105 0.015 −8×105 1.8 7.52×104 33.61 10 液态铅 1.20×105 0.015 −8×105 2.0 6.75×104 30.17 11 液态水 3.69×104 1.000 −8×105 1.4 1.08×105 473.86 表 3 传热关联式汇总
Table 3. Summary of Heat Transfer Correlations
研究者 工质 传热关联式 Rickard[19] Hg $Nu = 4.03 + 0.228Pe_{{{v}}\max }^{0.67}$ (21) Hsu[21] Hg $Nu = 0.958{\left( {\dfrac{{{\phi _1}}}{D}} \right)^{0.5}}Pe_{{v_{\max }}}^{0.5}{\left( {\dfrac{U}{{{U_{\max }}}}} \right)^{0.5}}$ (22) Dywer[23] Hg $Nu = 5.36 + 0.1974Pe_{v\max }^{0.682}$ (23) Kalish[24] NaK $Nu = {\left( {\dfrac{{{\phi _1}}}{D}} \right)^{0.5}}{\left( {1 - \dfrac{D}{P}} \right)^{0.5}}\left( {5.44 + 0.228Pe_{v\max }^{0.614}} \right)$ (24) Chernysh[25] Pb $Nu = 0.9 + 0.036P e_{v\max }^{0.8}$ (25) Umax—管间最小面积处平均流速,m/s;$\phi _1 $/D—与管束排布相关的解析解;P—常数 表 4 拟合参数信息
Table 4. Fitting Parameter Information
参数信息 a b c 数值 13.81742 0.04143 0.87505 标准误差 3.98418 0.06108 0.12104 95%置信区间下限 −4.86112 −0.20439 0.32226 95%置信区间上限 29.42395 0.32124 1.36384 相关性 0.96543 0.99961 0.99953 表 5 拟合统计信息
Table 5. Fitting Statistics
统计信息 数值 缩减卡方值 2.74337 残差平方和 5.48674 拟合结果中的相关系数R值 0.99828 R2 0.99656 调整后R2 0.99313 均方根误差 1.65631 -
[1] LU Y M, GUO Z P, GONG Y, et al. Optimal study of swordfish fin microchannel heat exchanger for the next generation nuclear power conversion system of lead-based reactor[J]. Annals of Nuclear Energy, 2022, 165: 108679. doi: 10.1016/j.anucene.2021.108679 [2] ALEMBERTI A. The lead fast reactor: an opportunity for the future?[J]. Engineering, 2016, 2(1): 59-62. doi: 10.1016/J.ENG.2016.01.022 [3] ZHANG Y, WANG C L, LAN Z K, et al. Review of thermal-hydraulic issues and studies of lead-based fast reactors[J]. Renewable and Sustainable Energy Reviews, 2020, 120: 109625. doi: 10.1016/j.rser.2019.109625 [4] 沈秀中,于平安,杨修周,等. 铅冷快堆固有安全性的分析[J]. 核动力工程,2002, 23(4): 75-78. doi: 10.3969/j.issn.0258-0926.2002.04.019 [5] BERSANO A, FALCONE N, BERTANI C, et al. Conceptual design of a bayonet tube steam generator with heat transfer enhancement using a helical coiled downcomer[J]. Progress in Nuclear Energy, 2018, 108: 243-252. doi: 10.1016/j.pnucene.2018.05.018 [6] GRASSO G, PETROVICH C, MATTIOLI D, et al. The core design of ALFRED, a demonstrator for the European lead-cooled reactors[J]. Nuclear Engineering and Design, 2014, 278: 287-301. doi: 10.1016/j.nucengdes.2014.07.032 [7] SUBKI H. Advances in small modular reactor technology developments[R]. Vienna, Austria: International Atomic Energy Agency, 2020. [8] 吕逸君. 大涡模拟液态金属在环形管道内的湍流传热特性[D]. 合肥: 中国科学技术大学,2015. [9] JENKINS R. Variation of the eddy conductivity with Prandtl modulus and its use in prediction of turbulent heat transfer coefficients[C]//Proceedings of the Heat Transfer and Fluid Mechanics Institute. Stanford University, 1951: 147-158. [10] AOKI S. A consideration on the heat transfer in liquid metal[J]. Bulletin of the Tokyo Institute of Technology, 1963, 54(3): 63-73. [11] REYNOLDS A J. The prediction of turbulent Prandtl and Schmidt numbers[J]. International Journal of Heat and Mass Transfer, 1975, 18(9): 1055-1069. doi: 10.1016/0017-9310(75)90223-9 [12] JISCHA M, RIEKE H B. About the prediction of turbulent Prandtl and Schmidt numbers from modeled transport equations[J]. International Journal of Heat and Mass Transfer, 1979, 22(11): 1547-1555. doi: 10.1016/0017-9310(79)90134-0 [13] CHENG X, TAK N I. Investigation on turbulent heat transfer to lead–bismuth eutectic flows in circular tubes for nuclear applications[J]. Nuclear Engineering and Design, 2006, 236(4): 385-393. doi: 10.1016/j.nucengdes.2005.09.006 [14] TALER D. Semi-empirical heat transfer correlations for turbulent tube flow of liquid metals[J]. International Journal of Numerical Methods for Heat & Fluid Flow, 2018, 28(1): 151-172. [15] KAYS W M, CRAWFORD M E. Convective heat and mass transfer[M]. New York: McGraw-Hill, 1980, 165-169. [16] KAYS W M. Turbulent prandtl number. Where are we?[J]. Journal of Heat Transfer, 1994, 116(2): 284-295. doi: 10.1115/1.2911398 [17] WEIGAND B, FERGUSON J R, CRAWFORD M E. An extended kays and crawford turbulent Prandtl number model[J]. International Journal of Heat and Mass Transfer, 1997, 40(17): 4191-4196. doi: 10.1016/S0017-9310(97)00084-7 [18] LEI X L, GUO Z M, WANG Y H, et al. Assessment and improvement on the applicability of turbulent-Prandtl-number models in RANS for liquid metals[J]. International Journal of Thermal Sciences, 2022, 171: 107260. doi: 10.1016/j.ijthermalsci.2021.107260 [19] RICKARD C L, DWYER O E, DROPKIN D. Heat-transfer rates to cross-flowing mercury in a staggered tube bank-II[J]. Journal of Fluids Engineering, 1958, 80(3): 646-652. [20] SUBBOTIN V I, MINASHIN V S, DENISKIN E I. Heat exchange in the transverse flow around tube bundles: NP-13712[R]. U. S. S. R. Sovet Ministrov, Gosudarstvennyi po Ispol'zovaniyu Atomnoi Energii, 1963. [21] CHIA-JUNG H. Analytical study of heat transfer to liquid metals in cross-flow through rod bundles[J]. International Journal of Heat and Mass Transfer, 1964, 7(4): 431-446. doi: 10.1016/0017-9310(64)90135-8 [22] HOE R, DROPKIN D, DWYER O E. Heat-transfer rates to crossflowing mercury in a staggered tube bank-I[J]. Journal of Fluids Engineering, 1957, 79(4): 899-905. [23] DWYER O E. Recent developments in liquid-metal heat transfer[J]. Atomic Energy Review, 1966, 4(1): 3-92. [24] KALISH S, DWYER O E. Heat transfer to NaK flowing through unbaffled rod bundles[J]. International Journal of Heat and Mass Transfer, 1967, 10(11): 1533-1558. doi: 10.1016/0017-9310(67)90006-3 [25] CHERNYSH A, IARMONOV M, MAKHOV K, et al. Experimental study of the characteristics of heat transfer in an HLMC cross-flow around tubes[J]. Journal of Nuclear Engineering and Radiation Science, 2015, 1(4): 041015. doi: 10.1115/1.4030365 -





 下载:
下载: